【同步精讲-习题课件】第19章《一次函数》专题训练(七) 利用图象解决应用题-人教版数学八下
文档属性
| 名称 | 【同步精讲-习题课件】第19章《一次函数》专题训练(七) 利用图象解决应用题-人教版数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:56 | ||
图片预览



文档简介
(共10张PPT)
专题训练(七) 利用图象解决应用题
第十九章 一次函数
必
●
类型1折线型
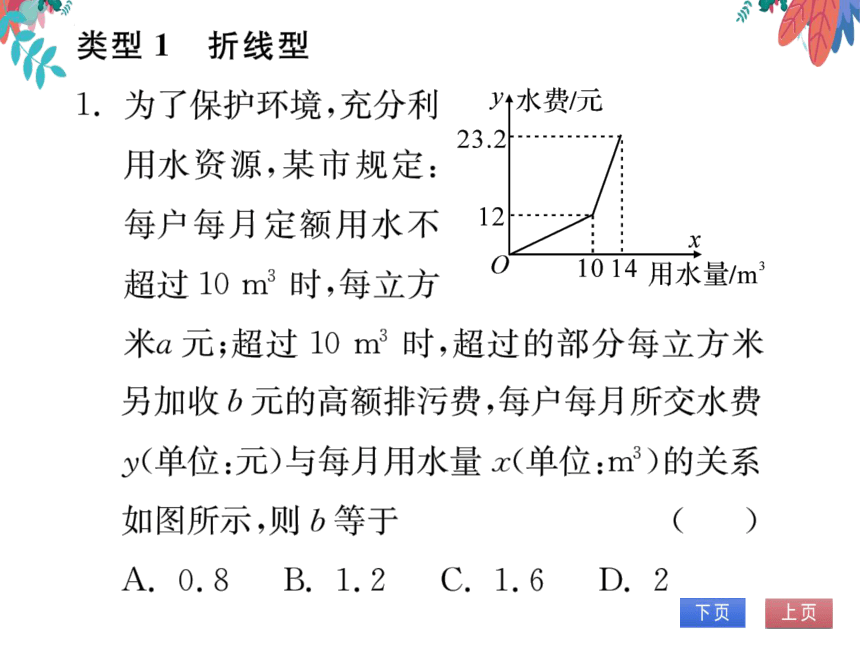
1.为了保护环境,充分利
y水费/元
23.2
用水资源,某市规定:
每户每月定额用水不
12
X
超过10m3时,每立方
1014用水量/m
米a元;超过l0m3时,超过的部分每立方米
另加收b元的高额排污费,每户每月所交水费
y(单位:元)与每月用水量x(单位:m)的关系
如图所示,则b等于
(
A.0.8
B.1.2
C.1.6
D.2
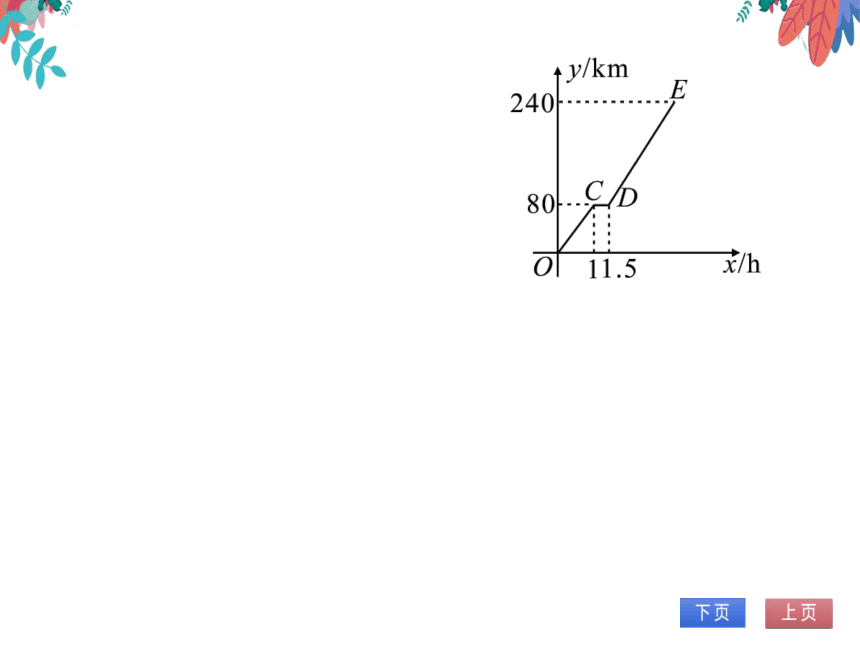
2.(2021·江苏淮安)甲、乙两地的路程为
290km,一辆汽车早上8:00从甲地出发,
匀速向乙地行驶,途中休息一段时间后,按
原速继续前进,当离甲地路程为240km时
接到通知,要求中午12:00准时到达乙地.
设汽车出发xh后离甲地的路程为ykm,
图中折线OCDE表示接到通知前y与x
之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度
为
80
km/h;
(2)求线段DE所表示的y与x之间的函
数解析式;
(3)接到通知后,汽车仍按原速行驶能否准
时到达?请说明理由.
解:(2)休息后按原速继续前进行驶
ty/km
240.
的时间为(240一80)÷80=2(h),2
+1.5=3.5(h).
80
。点E的坐标为((3.5,240),
011.5
/h
设线段DE所表示的y与x之间的
函数解析式为y=kx十b,则:
1.5k+b=80,
k=80,
解得
3.5k+b=240.
b=一40.
.线段DE所表示的y与x之间的函数解析式为y=80x
-40(1.5x≤3.5).
(3)接到通知后,汽车仍按原速行驶,则全程所需时间为
290÷80+0.5=4.125(h),
12:00-8:00=4(h),4.125>4.
.接到通知后,汽车仍按原速行驶不能准时到达.
类型2
双线型
3.(2022·长春)已知A、B两地之间有一条
长440千米的高速公路.甲、乙两车分别从
A、B两地同时出发,沿此公路相向而行,甲
车先以100千米/时的速度匀速行驶
200千米后与乙车相遇,再以另一速度继续
匀速行驶4小时到达B地;乙车匀速行驶
至A地,两车到达各自的目的地后停止,两
车距A地的路程y(千米)与各自的行驶时
间x(时)之间的函数关系如图所示.
(1)m=2,n=
6
(2)求两车相遇后,甲车距A地的路程y与
x之间的函数关系式;
(3)当乙车到达A地时,求甲车距A地的
路程.
专题训练(七) 利用图象解决应用题
第十九章 一次函数
必
●
类型1折线型
1.为了保护环境,充分利
y水费/元
23.2
用水资源,某市规定:
每户每月定额用水不
12
X
超过10m3时,每立方
1014用水量/m
米a元;超过l0m3时,超过的部分每立方米
另加收b元的高额排污费,每户每月所交水费
y(单位:元)与每月用水量x(单位:m)的关系
如图所示,则b等于
(
A.0.8
B.1.2
C.1.6
D.2
2.(2021·江苏淮安)甲、乙两地的路程为
290km,一辆汽车早上8:00从甲地出发,
匀速向乙地行驶,途中休息一段时间后,按
原速继续前进,当离甲地路程为240km时
接到通知,要求中午12:00准时到达乙地.
设汽车出发xh后离甲地的路程为ykm,
图中折线OCDE表示接到通知前y与x
之间的函数关系.
(1)根据图象可知,休息前汽车行驶的速度
为
80
km/h;
(2)求线段DE所表示的y与x之间的函
数解析式;
(3)接到通知后,汽车仍按原速行驶能否准
时到达?请说明理由.
解:(2)休息后按原速继续前进行驶
ty/km
240.
的时间为(240一80)÷80=2(h),2
+1.5=3.5(h).
80
。点E的坐标为((3.5,240),
011.5
/h
设线段DE所表示的y与x之间的
函数解析式为y=kx十b,则:
1.5k+b=80,
k=80,
解得
3.5k+b=240.
b=一40.
.线段DE所表示的y与x之间的函数解析式为y=80x
-40(1.5x≤3.5).
(3)接到通知后,汽车仍按原速行驶,则全程所需时间为
290÷80+0.5=4.125(h),
12:00-8:00=4(h),4.125>4.
.接到通知后,汽车仍按原速行驶不能准时到达.
类型2
双线型
3.(2022·长春)已知A、B两地之间有一条
长440千米的高速公路.甲、乙两车分别从
A、B两地同时出发,沿此公路相向而行,甲
车先以100千米/时的速度匀速行驶
200千米后与乙车相遇,再以另一速度继续
匀速行驶4小时到达B地;乙车匀速行驶
至A地,两车到达各自的目的地后停止,两
车距A地的路程y(千米)与各自的行驶时
间x(时)之间的函数关系如图所示.
(1)m=2,n=
6
(2)求两车相遇后,甲车距A地的路程y与
x之间的函数关系式;
(3)当乙车到达A地时,求甲车距A地的
路程.
