【同步精讲-习题课件】第17章《勾股定理》17.1 第2课时 勾股定理的应用-人教版数学八下
文档属性
| 名称 | 【同步精讲-习题课件】第17章《勾股定理》17.1 第2课时 勾股定理的应用-人教版数学八下 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 11:53:56 | ||
图片预览







文档简介
(共21张PPT)
17.1 第2课时 勾股定理的应用
第十七章 勾股定理
必
●
知识要点全练
夯实基础
o0000000000000000000000000000000000
知识点1
勾股定理的实际应用
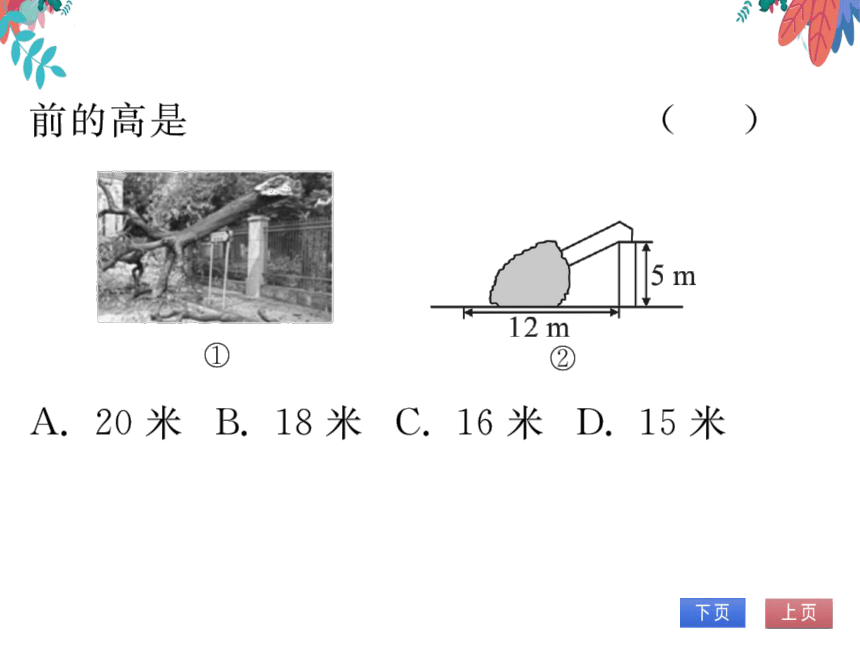
1.(2022秋·太原月考)如图①,一棵大树在
一次强烈的地震中于离地面5米处折断倒
下,树顶落在离树根12米处,图②是这棵
大树折断的示意图,则这棵大树在折断之
前的高是
(B)
12m
①
②
A.20米B.18米C.16米D.15米
2.(2022秋·龙口期末)一架长5m的梯子斜
靠在墙上,梯子底端到墙的距离为3m.若
梯子顶端下滑1m,那么梯子底端在水平方
向上滑动了
(A)
A.1 m
B.小于1m
C.大于1m
D.无法确定
3.(2023·山东东营)一艘船由A港沿北偏东
60°方向航行30km至B港然后沿北偏西
30°方向航行40km至C港,则AC两港之
间的距离为
50
km.
4.(2023春·灵石县期中)如图所示的人字梯
撑开后侧面是一个等腰三角形,若梯子长
AB等于2.5m,梯子完全撑开后顶端离地
面的高度AD等于2.4m,则此时梯子侧面
宽度BC等于1.4
m.
A
B
D
C
(第4题图)
知识点2在数轴上表示无理数
5.(2022秋·自贡期末)如图,已知A(1,2),连
接OA,以原点O为圆心,OA长为半径画弧,交
x轴正半轴于点B,则点B坐标为
(
A.(0,2)
B.(0,/5)
C.(2,0)
D.(/5,0)
A
B
X
(第5题图)
6.(2022秋·南京期末)如
D
A
图,矩形ABCD
中,
2
AB=3,AD=1,AB在数轴上,且点A表
示的数为一1,若以点A为圆心,对角线AC
的长为半径作弧交数轴的正半轴于点M,
则点M表示的实数为
/10-1
知识点3
勾股定理与网格图形
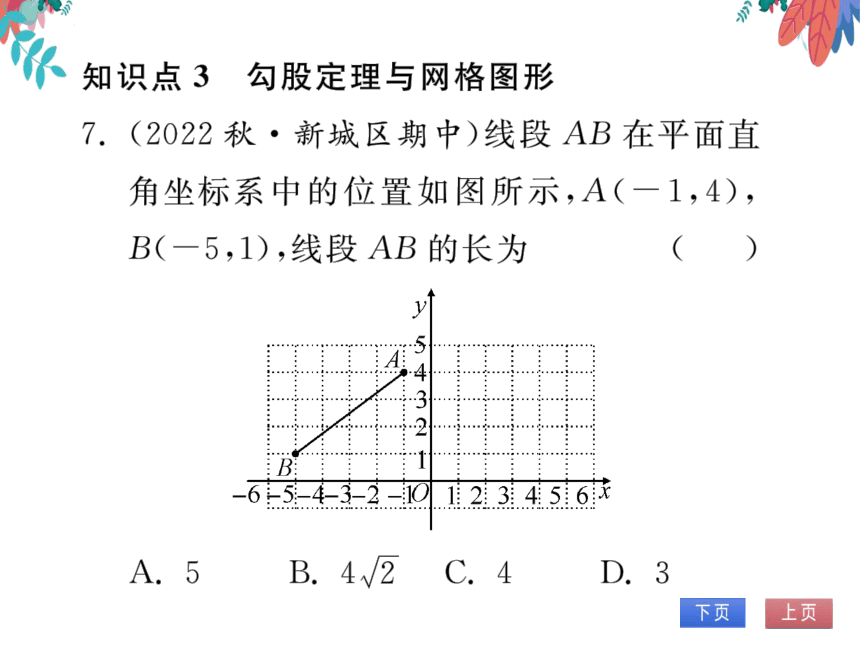
7.(2022秋·新城区期中)线段AB在平面直
角坐标系中的位置如图所示,A(一1,4),
B(一5,1),线段AB的长为
(A)
■■■
5
:B:
-65-4-3-2-10123456
A.5
B.4√/2
C.4
D.3
8.(2022秋·碑林区月考)如图,在边长为1
的正方形网格中,A、B、C均在正方形格点
上,则C点到AB的距离为
(D)
A.
3/10
B.2而C.510
D
./10
10
5
4
5
17.1 第2课时 勾股定理的应用
第十七章 勾股定理
必
●
知识要点全练
夯实基础
o0000000000000000000000000000000000
知识点1
勾股定理的实际应用
1.(2022秋·太原月考)如图①,一棵大树在
一次强烈的地震中于离地面5米处折断倒
下,树顶落在离树根12米处,图②是这棵
大树折断的示意图,则这棵大树在折断之
前的高是
(B)
12m
①
②
A.20米B.18米C.16米D.15米
2.(2022秋·龙口期末)一架长5m的梯子斜
靠在墙上,梯子底端到墙的距离为3m.若
梯子顶端下滑1m,那么梯子底端在水平方
向上滑动了
(A)
A.1 m
B.小于1m
C.大于1m
D.无法确定
3.(2023·山东东营)一艘船由A港沿北偏东
60°方向航行30km至B港然后沿北偏西
30°方向航行40km至C港,则AC两港之
间的距离为
50
km.
4.(2023春·灵石县期中)如图所示的人字梯
撑开后侧面是一个等腰三角形,若梯子长
AB等于2.5m,梯子完全撑开后顶端离地
面的高度AD等于2.4m,则此时梯子侧面
宽度BC等于1.4
m.
A
B
D
C
(第4题图)
知识点2在数轴上表示无理数
5.(2022秋·自贡期末)如图,已知A(1,2),连
接OA,以原点O为圆心,OA长为半径画弧,交
x轴正半轴于点B,则点B坐标为
(
A.(0,2)
B.(0,/5)
C.(2,0)
D.(/5,0)
A
B
X
(第5题图)
6.(2022秋·南京期末)如
D
A
图,矩形ABCD
中,
2
AB=3,AD=1,AB在数轴上,且点A表
示的数为一1,若以点A为圆心,对角线AC
的长为半径作弧交数轴的正半轴于点M,
则点M表示的实数为
/10-1
知识点3
勾股定理与网格图形
7.(2022秋·新城区期中)线段AB在平面直
角坐标系中的位置如图所示,A(一1,4),
B(一5,1),线段AB的长为
(A)
■■■
5
:B:
-65-4-3-2-10123456
A.5
B.4√/2
C.4
D.3
8.(2022秋·碑林区月考)如图,在边长为1
的正方形网格中,A、B、C均在正方形格点
上,则C点到AB的距离为
(D)
A.
3/10
B.2而C.510
D
./10
10
5
4
5
