人教A版(2019)高中数学选择性必修2 4.1.2数列的概念 课件
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修2 4.1.2数列的概念 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-01 14:40:01 | ||
图片预览








文档简介
(共26张PPT)
章节:第四章 数列
标题:4.1数列的概念
课时:2课时
(第二课时)
目
录
1.教学目标
2.新课讲授
3.新课小结
4.作业巩固
PART 01
教学目标
环节1:教学目标分解
教学目标 素养目标
1.经历数列概念的抽象过程,了解数列的定义,了解数列的表示方法 数学抽象逻辑推理
数学运算
2.经历从函数的角度研究数列一般形式的过程,了解数列是一种特殊的函数,能通过对数列的表示(列表法和图象法)体会其特殊性 3.了解数列递推公式的定义,能根据数列的递推公式求该数列的项.了解数列前n项和公式的定义,掌握通项公式与前n项和公式的关系,能根据数列前n项和公式求该数列的通项公式 环节2:教学重难点
重点:
1.经历数列概念的抽象过程,了解数列的定义,了解数列的表示方法(列表法和图象法)。
2.理解数列的通项公式表示的是数列的项及其项数之间的对应关系,能根据数列的递推公式求该数列的项。
难点:根据数列的递推公式求数列的通项
PART 02
新课讲授
探究四:数列的递推公式
课堂例题
例3.如果数列的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
l
解:令,
解这个关于的方程,得(舍去),或.
所以,120是数列的项,是第10项.
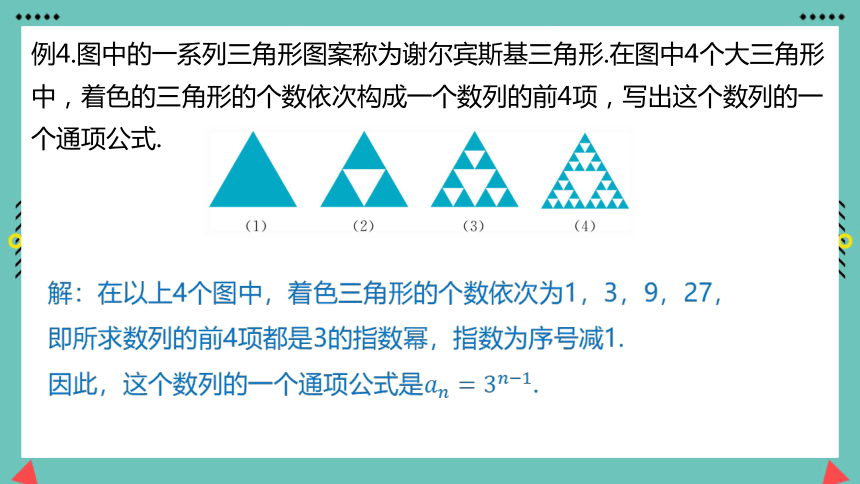
例4.图中的一系列三角形图案称为谢尔宾斯基三角形.在图中4个大三角形中,着色的三角形的个数依次构成一个数列的前4项,写出这个数列的一个通项公式.
解:在以上4个图中,着色三角形的个数依次为1,3,9,27,
即所求数列的前4项都是3的指数幂,指数为序号减1.
因此,这个数列的一个通项公式是.
换个角度观察图中的4个图形.可以发现,,且每个图形中的着色三角形都在下一个图形中分裂为3个着色小三角形和1个无色小三角形.于是从第2个图形开始,每个图形中着色三角形的个数都是前一个图形中着色三角形个数的3倍.这样,例4中的数列的前4项满足,,,.
因此猜测这个数列满足公式
当不能明显看出数列的项的取值规律时,可以尝试通过运算来寻找规律.如依次取出数列的某一项,减去或除以它的前一项,再对差或商加以观察.
像这样,如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.知道了首项或前几项以及递推公式,就能求出数列的每一项了.
概念3:
探究五:数列的前n项和公式
l
课堂例题
l
例5.已知数列的首项为,递推公式为,写出这个数列的前5项.
l
解:由题意可知,,
概念4:
在对数列的研究中,求数列某些项的和是主要问题之一.我们把数列从第1项起到第项止的各项之和,称为数列的前项和,记作,即
.
如果数列的前项和与它的序号之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前项和公式.
显然,而,于是我们有
l
问题3:已知数列的前项和公式为,你能求出的通项公式吗?
l
解:∵
并且当时,依然成立.
所以的通项公式是.
l
PART 03
新课小结
像这样,如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.知道了首项或前几项以及递推公式,就能求出数列的每一项了.
概念3:
概念4:
在对数列的研究中,求数列某些项的和是主要问题之一.我们把数列从第1项起到第项止的各项之和,称为数列的前项和,记作,即
.
如果数列的前项和与它的序号之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前项和公式.
显然,而,于是我们有
PART 04
作业巩固
课本P5 练习
课本P9 习题4.1
非常感谢您的观看
章节:第四章 数列
标题:4.1数列的概念
课时:2课时
(第二课时)
目
录
1.教学目标
2.新课讲授
3.新课小结
4.作业巩固
PART 01
教学目标
环节1:教学目标分解
教学目标 素养目标
1.经历数列概念的抽象过程,了解数列的定义,了解数列的表示方法 数学抽象逻辑推理
数学运算
2.经历从函数的角度研究数列一般形式的过程,了解数列是一种特殊的函数,能通过对数列的表示(列表法和图象法)体会其特殊性 3.了解数列递推公式的定义,能根据数列的递推公式求该数列的项.了解数列前n项和公式的定义,掌握通项公式与前n项和公式的关系,能根据数列前n项和公式求该数列的通项公式 环节2:教学重难点
重点:
1.经历数列概念的抽象过程,了解数列的定义,了解数列的表示方法(列表法和图象法)。
2.理解数列的通项公式表示的是数列的项及其项数之间的对应关系,能根据数列的递推公式求该数列的项。
难点:根据数列的递推公式求数列的通项
PART 02
新课讲授
探究四:数列的递推公式
课堂例题
例3.如果数列的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
l
解:令,
解这个关于的方程,得(舍去),或.
所以,120是数列的项,是第10项.
例4.图中的一系列三角形图案称为谢尔宾斯基三角形.在图中4个大三角形中,着色的三角形的个数依次构成一个数列的前4项,写出这个数列的一个通项公式.
解:在以上4个图中,着色三角形的个数依次为1,3,9,27,
即所求数列的前4项都是3的指数幂,指数为序号减1.
因此,这个数列的一个通项公式是.
换个角度观察图中的4个图形.可以发现,,且每个图形中的着色三角形都在下一个图形中分裂为3个着色小三角形和1个无色小三角形.于是从第2个图形开始,每个图形中着色三角形的个数都是前一个图形中着色三角形个数的3倍.这样,例4中的数列的前4项满足,,,.
因此猜测这个数列满足公式
当不能明显看出数列的项的取值规律时,可以尝试通过运算来寻找规律.如依次取出数列的某一项,减去或除以它的前一项,再对差或商加以观察.
像这样,如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.知道了首项或前几项以及递推公式,就能求出数列的每一项了.
概念3:
探究五:数列的前n项和公式
l
课堂例题
l
例5.已知数列的首项为,递推公式为,写出这个数列的前5项.
l
解:由题意可知,,
概念4:
在对数列的研究中,求数列某些项的和是主要问题之一.我们把数列从第1项起到第项止的各项之和,称为数列的前项和,记作,即
.
如果数列的前项和与它的序号之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前项和公式.
显然,而,于是我们有
l
问题3:已知数列的前项和公式为,你能求出的通项公式吗?
l
解:∵
并且当时,依然成立.
所以的通项公式是.
l
PART 03
新课小结
像这样,如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.知道了首项或前几项以及递推公式,就能求出数列的每一项了.
概念3:
概念4:
在对数列的研究中,求数列某些项的和是主要问题之一.我们把数列从第1项起到第项止的各项之和,称为数列的前项和,记作,即
.
如果数列的前项和与它的序号之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前项和公式.
显然,而,于是我们有
PART 04
作业巩固
课本P5 练习
课本P9 习题4.1
非常感谢您的观看
