高一物理必修13.1力的分解课件
文档属性
| 名称 | 高一物理必修13.1力的分解课件 |  | |
| 格式 | zip | ||
| 文件大小 | 378.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2015-04-23 10:17:34 | ||
图片预览


文档简介
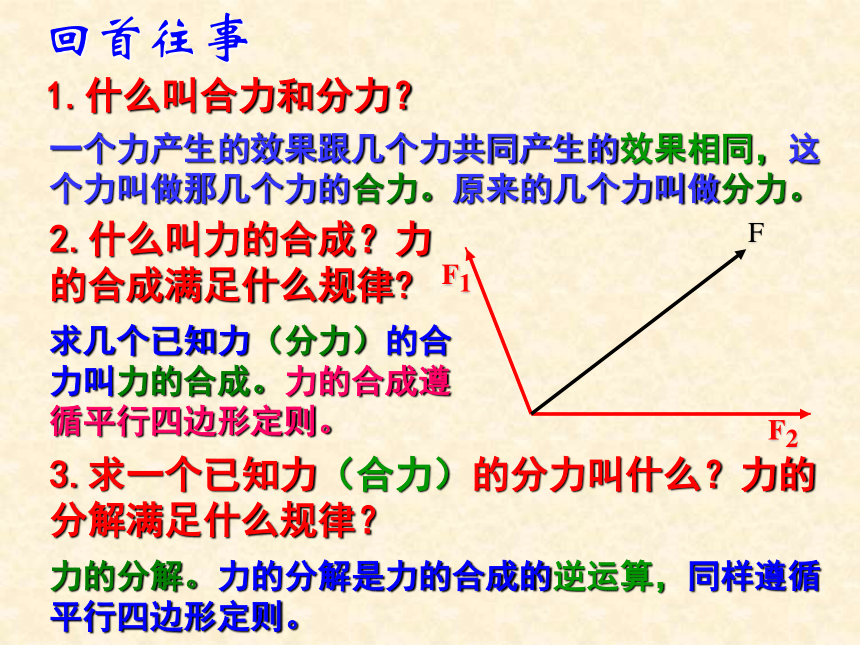
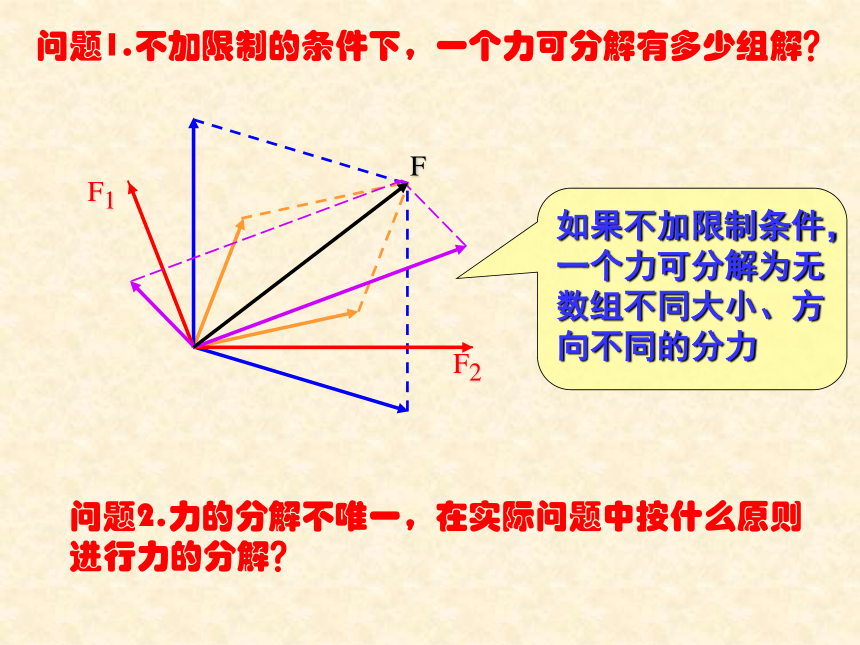
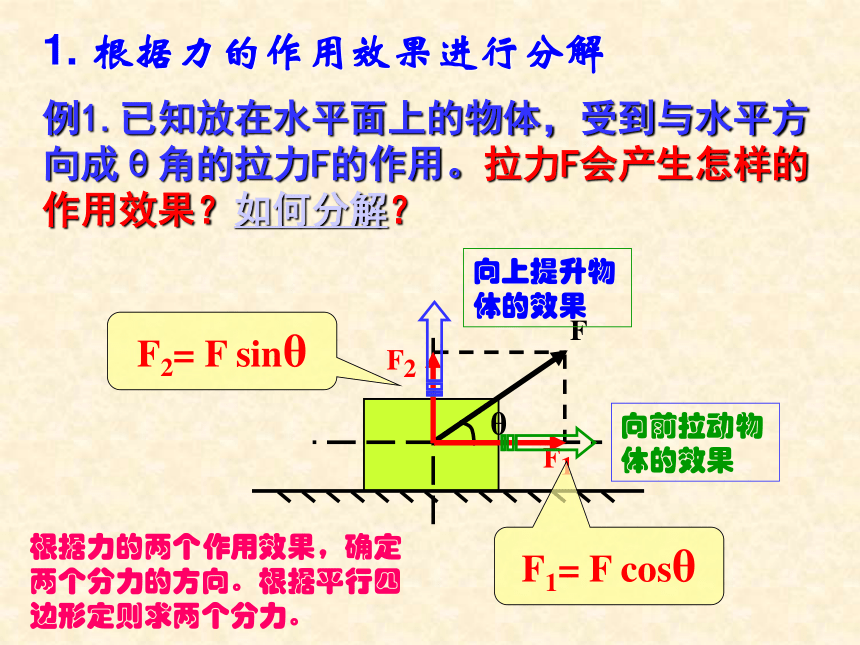
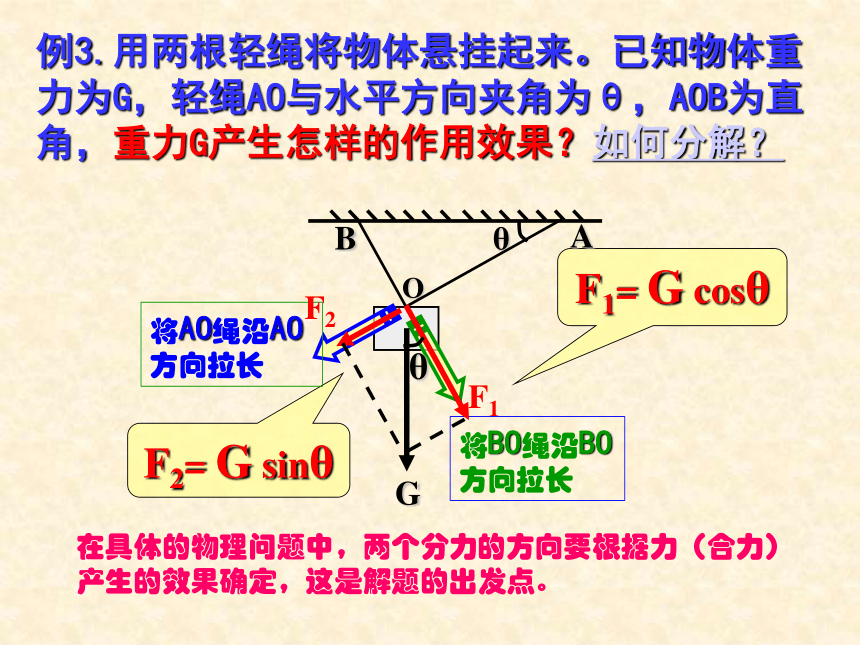
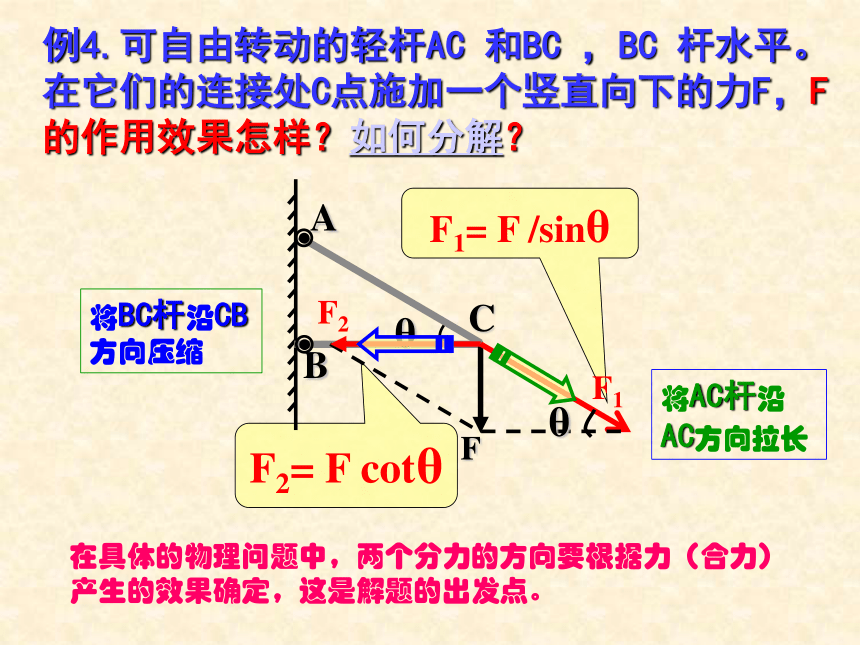
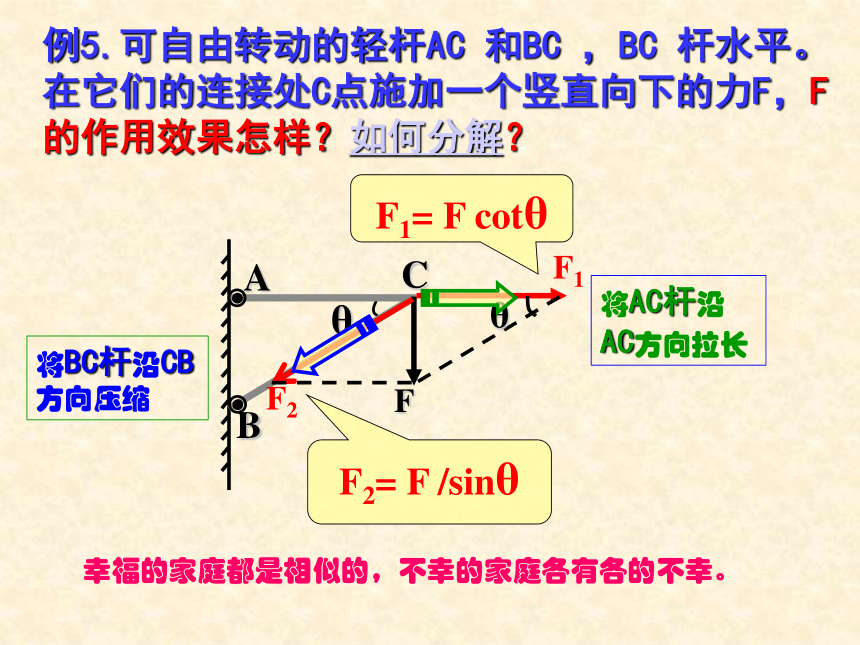
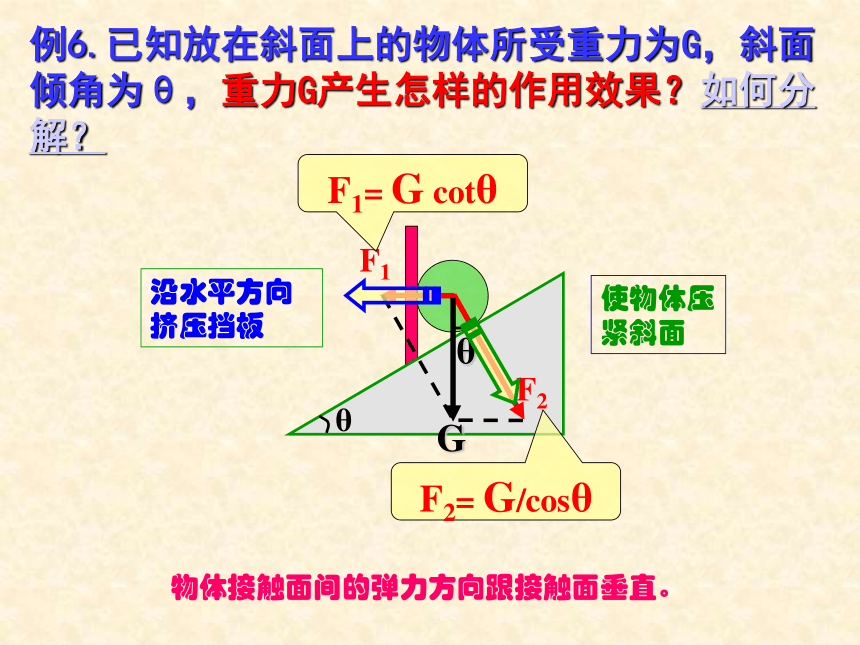
课件23张PPT。§1.6 力的分解第一章 力 1.什么叫合力和分力?2.什么叫力的合成?力的合成满足什么规律?3.求一个已知力(合力)的分力叫什么?力的分解满足什么规律?回首往事求几个已知力(分力)的合力叫力的合成。力的合成遵循平行四边形定则。一个力产生的效果跟几个力共同产生的效果相同,这个力叫做那几个力的合力。原来的几个力叫做分力。力的分解。力的分解是力的合成的逆运算,同样遵循平行四边形定则。问题1.不加限制的条件下,一个力可分解有多少组解?如果不加限制条件,一个力可分解为无数组不同大小、方向不同的分力问题2.力的分解不唯一,在实际问题中按什么原则进行力的分解?例1.已知放在水平面上的物体,受到与水平方向成θ角的拉力F的作用。拉力F会产生怎样的作用效果?如何分解?F2= F sinθF1= F cosθ1. 根据力的作用效果进行分解根据力的两个作用效果,确定两个分力的方向。根据平行四边形定则求两个分力。例2.已知放在斜面上的物体所受重力为G,斜面倾角为θ,重力G产生怎样的作用效果?如何分解?F1= G sinθF2= G cosθ根据力的作用效果做出平行四边形,变成一个解三角形的数学问题,一般是直角三角形,不外乎三角函数和勾股定理。这样将一个力的分解的物理问题转化为一个解三角形的数学问题。思考:当θ增大时,F1、F2如何变化?例3.用两根轻绳将物体悬挂起来。已知物体重力为G,轻绳AO与水平方向夹角为θ,AOB为直角,重力G产生怎样的作用效果?如何分解?F1= G cosθF2= G sinθ在具体的物理问题中,两个分力的方向要根据力(合力)产生的效果确定,这是解题的出发点。例4.可自由转动的轻杆AC 和BC ,BC 杆水平。在它们的连接处C点施加一个竖直向下的力F,F 的作用效果怎样?如何分解?F1= F /sinθF2= F cotθ在具体的物理问题中,两个分力的方向要根据力(合力)产生的效果确定,这是解题的出发点。例5.可自由转动的轻杆AC 和BC ,BC 杆水平。在它们的连接处C点施加一个竖直向下的力F,F 的作用效果怎样?如何分解?F1= F cotθF2= F /sinθ幸福的家庭都是相似的,不幸的家庭各有各的不幸。例6.已知放在斜面上的物体所受重力为G,斜面倾角为θ,重力G产生怎样的作用效果?如何分解?F1= G cotθF2= G/cosθ物体接触面间的弹力方向跟接触面垂直。例7.已知放在斜面上的物体所受重力为G,斜面倾角为θ,重力G产生怎样的作用效果?如何分解?F2= G cosθF1= G sinθ物理实际问题确定两个分力的方向力的作用效果
平行四边形定则作平行四边形平面几何 三角函数
解三角形回归物理物理问题数学问题分析讨论平行四边形定则⑵采用正交分解法求合力。②正交分解各力,即分别将各力投影在坐标轴上,分别求出坐标轴上各力投影的合力。为了合成而分解退一步海阔天空,⑴定义:把力沿着两个选定的互相垂直的方向分解,叫做力的正交分解法。2. 正交分解①正确选择直角坐标系,一般选共点力的作用点为原点,水平方向或物体运动的加速度方向为X轴,使尽量多的力在坐标轴上。例1. 质量为m的木块在推力F作用下,在水平地面上做匀速运动,如图所示,已知木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力为 ( )
A.μmg
B.μ(mg+Fsinθ)
C.μ(mg-Fsinθ)
D.FcosθB D 正交分解的原则(1)是让更多的力落在坐标轴上; (2)物体处于平衡状态有∑Fx=0 ① ∑Fy=0 ② 。培养辩证唯物主义观点分析问题,全面地、变化地看问题。比如为了求合力进行正交分解,分解是方法,合成是目的。例2.已知物体沿斜面匀速下滑,斜面与地面间的夹角为θ,求物体与斜面间的动摩擦因数。解:把重力沿斜面和垂直于斜面方向正交分解有物体处于平衡状态根据滑动摩擦力的计算公式联立以上各式解出所谓“正交分解”,是把力沿两个选定的互相垂直的方向进行分解的方法,其目的是便于运用代数运算公式来解决矢量的运算,是处理复杂的力的合成与分解问题的一种简单的方法。特别是应用在受力分析中,显得简便易行。问题3.将一个已知力分解的四种情况⑴已知两个分力的方向——唯一解⑵已知一个分力的大小和方向——唯一解只能唯一的作出力的平行四边形只能唯一的作出力的平行四边形(3)若已知一个分力F1的大小和另一分力F2的方向(即已知F2和F的夹角θ),将一已知力F分解,其结果有下面五种可能。① F1< Fsinθ② F1= Fsinθ相离相切无解一解③ Fsinθ F一解F2F1(4)已知两个分力F1、 F2的大小,将一个已知力F分解,其结果有下面三种可能。② F=F1 + F2 或 F=F1 – F2① F>F1 + F2或F < ∣ F1 – F2∣无解一解以这三个力的大小为边长不能构成一个三角形同一条直线上力的分解③∣F1 – F2∣< F < F1 + F2无数解(一个平面内有两解)以这三个力的大小为边长能构成一个三角形。1.力的分解是力的合成的逆运算。力的合成和分解都满足平行四边形定则。前者是已知两个邻边求对角线,后者是已知对角线求两个邻边。小结力的分解不具有唯一性2. 力的分解的原则如果没有其它限制,一个力可以分解成无数对大小、方向不同的分力。⑴ 理论角度①无条件限制基本原则(I)——无条件限制的分解具有任意性。②有条件限制条件1:已知两个分力的方向——唯一解条件2:已知一个分力的大小和方向——唯一解条件3:若已知一个分力F1的大小和另一分力F2的方向(即已知F2和F的夹角θ),将一已知力F分解,其结果有下面五种可能。由力产生的效果确定分力的方向,由平行四边形定则(或三角形定则)确定分力的大小。⑵ 实际角度(将一个实际的力分解)①按力的实际作用效果分解条件4:已知两个分力F1、 F2的大小,将一个已知力F分解,其结果有下面三种可能。基本原则(II)——有条件限制的分解根据具体条件物理实际问题确定两个分力的方向力的作用效果
平行四边形定则作平行四边形平面几何 三角函数
解三角形回归物理物理问题数学问题分析讨论平行四边形定则解决力的分解问题的实际问题的思路和方法比如为了求合力进行正交分解,分解是方法,合成是目的。②按问题的需要进行分解基本原则(Ⅲ)——在具体的物理问题中,两个分力的方向要根据力产生的效果或者把力沿两个选定的互相垂直的方向进行分解。所谓“正交分解”,是把力沿两个选定的互相垂直的方向进行分解的方法,其目的是便于运用代数运算公式来解决矢量的运算,是处理复杂的力的合成与分解问题的一种简单的方法。特别是应用在受力分析中,显得简便易行。
平行四边形定则作平行四边形平面几何 三角函数
解三角形回归物理物理问题数学问题分析讨论平行四边形定则⑵采用正交分解法求合力。②正交分解各力,即分别将各力投影在坐标轴上,分别求出坐标轴上各力投影的合力。为了合成而分解退一步海阔天空,⑴定义:把力沿着两个选定的互相垂直的方向分解,叫做力的正交分解法。2. 正交分解①正确选择直角坐标系,一般选共点力的作用点为原点,水平方向或物体运动的加速度方向为X轴,使尽量多的力在坐标轴上。例1. 质量为m的木块在推力F作用下,在水平地面上做匀速运动,如图所示,已知木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力为 ( )
A.μmg
B.μ(mg+Fsinθ)
C.μ(mg-Fsinθ)
D.FcosθB D 正交分解的原则(1)是让更多的力落在坐标轴上; (2)物体处于平衡状态有∑Fx=0 ① ∑Fy=0 ② 。培养辩证唯物主义观点分析问题,全面地、变化地看问题。比如为了求合力进行正交分解,分解是方法,合成是目的。例2.已知物体沿斜面匀速下滑,斜面与地面间的夹角为θ,求物体与斜面间的动摩擦因数。解:把重力沿斜面和垂直于斜面方向正交分解有物体处于平衡状态根据滑动摩擦力的计算公式联立以上各式解出所谓“正交分解”,是把力沿两个选定的互相垂直的方向进行分解的方法,其目的是便于运用代数运算公式来解决矢量的运算,是处理复杂的力的合成与分解问题的一种简单的方法。特别是应用在受力分析中,显得简便易行。问题3.将一个已知力分解的四种情况⑴已知两个分力的方向——唯一解⑵已知一个分力的大小和方向——唯一解只能唯一的作出力的平行四边形只能唯一的作出力的平行四边形(3)若已知一个分力F1的大小和另一分力F2的方向(即已知F2和F的夹角θ),将一已知力F分解,其结果有下面五种可能。① F1< Fsinθ② F1= Fsinθ相离相切无解一解③ Fsinθ
平行四边形定则作平行四边形平面几何 三角函数
解三角形回归物理物理问题数学问题分析讨论平行四边形定则解决力的分解问题的实际问题的思路和方法比如为了求合力进行正交分解,分解是方法,合成是目的。②按问题的需要进行分解基本原则(Ⅲ)——在具体的物理问题中,两个分力的方向要根据力产生的效果或者把力沿两个选定的互相垂直的方向进行分解。所谓“正交分解”,是把力沿两个选定的互相垂直的方向进行分解的方法,其目的是便于运用代数运算公式来解决矢量的运算,是处理复杂的力的合成与分解问题的一种简单的方法。特别是应用在受力分析中,显得简便易行。
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
