30.5 二次函数与一元二次方程的关系分层练习-冀教版数学九年级下册(含答案)
文档属性
| 名称 | 30.5 二次函数与一元二次方程的关系分层练习-冀教版数学九年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 542.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
30.5二次函数与一元二次方程的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛物线与直线交于两点,若,则关于直线;甲答:一定经过一、四象限,乙答:一定经过一、三象限.则正确的是( )
A.甲乙均错 B.甲乙均对 C.甲错乙对 D.甲对乙错
2.已知二次函数y=x2+bx-2的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是 ( )
A.(3,0) B.(2,0) C.(-2,0) D.(-1,0)
3.观察下列表格,求一元二次方程x2﹣x=1.1的一个近似解是( )
x 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
x2﹣x 0.11 0.24 0.39 0.56 0.75 0.96 1.19 1.44 1.71
A.0.11 B.1.6 C.1.7 D.1.19
4.定义min{a,b,c}为a,b,c中的最小值,例如:min{5,3,1}=1,min{8,5,5}=5.如果min{4,x2﹣4x,﹣3}=﹣3,那么x的取值范围是( )
A.1≤x≤3 B.x≤1或x≥3 C.1<x<3 D.x<1或x>3
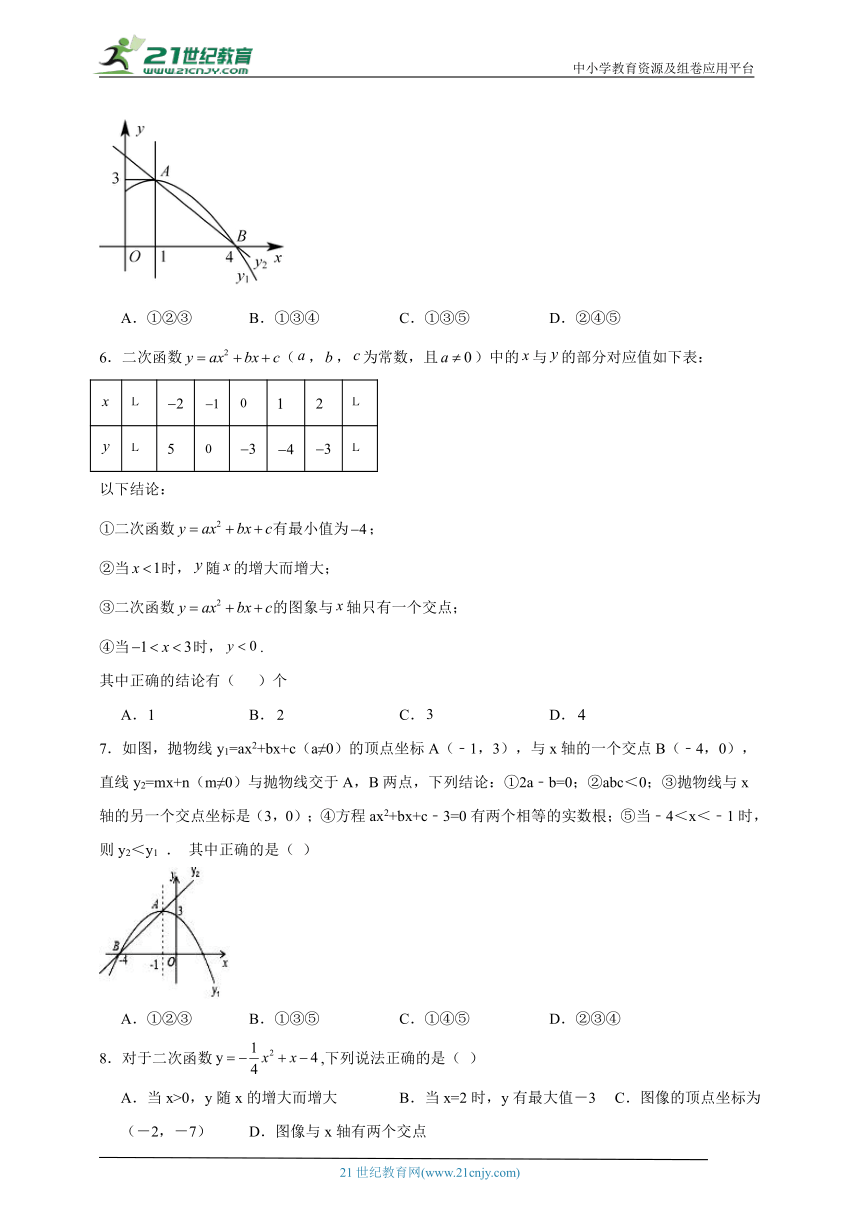
5.如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
6.二次函数(,,为常数,且)中的与的部分对应值如下表:
以下结论:
①二次函数有最小值为;
②当时,随的增大而增大;
③二次函数的图象与轴只有一个交点;
④当时,.
其中正确的结论有( )个
A. B. C. D.
7.如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1 . 其中正确的是( )
A.①②③ B.①③⑤ C.①④⑤ D.②③④
8.对于二次函数,下列说法正确的是( )
A.当x>0,y随x的增大而增大 B.当x=2时,y有最大值-3 C.图像的顶点坐标为(-2,-7) D.图像与x轴有两个交点
9.抛物线的对称轴为直线x=1,与x轴的一个交点坐标为(, 0),其部分图象如图所示.下列结论:①;②方程的两个根是;③;④当时,x的取值范围是;⑤m为任意实数,其中结论正确的个数是( )
A.4个 B.3个 C.2个 D.1个
10.若关于的一元二次方程有两个不同的实数根,,方程有两个不同的实数根,,则,,,的大小关系为( )
A.pC.m二、填空题
11.已知函数y1=(a2+1)x2+bx+c,y2=-x+2,若方程(a2+1)x2+(b+1)x+c-2=0的两根分别为x1=-2,x2=8,则使y1> y2,成立的x的取值范围是 .
12.已知抛物线的对称轴是x=m,若该抛物线与x轴交于(1,0),(3,0)两点,则m的值为
13.若二次函数y=(k﹣2)x2﹣2x+1与x轴有交点,则k的取值范围为 .
14.抛物线与直线的两个交点的横坐标分别是,,记,则代数式的值为 .
15.在平面直角坐标系中,与抛物线关于轴成轴对称的抛物线的解析式是
16.如图,在平面直角坐标系中,抛物线与x轴交于点A,点P在抛物线上,连接.若是以为底边的等腰三角形,则的面积是 .
17.抛物线与x轴交于点A,B,则线段AB的长度是 .
18.已知函数的图象如图所示,若直线与该图象只有一个交点,则m的取值范围为 .
19.二次函数y=x2-4x+3的图象交x轴于A、B两点,交y 轴于点C,则△ABC的面积为
20.已知二次函数y=x2﹣5x+m的图象与x轴有两个交点,若其中一个交点的坐标为(1,0),则另一个交点的坐标为 .
三、解答题
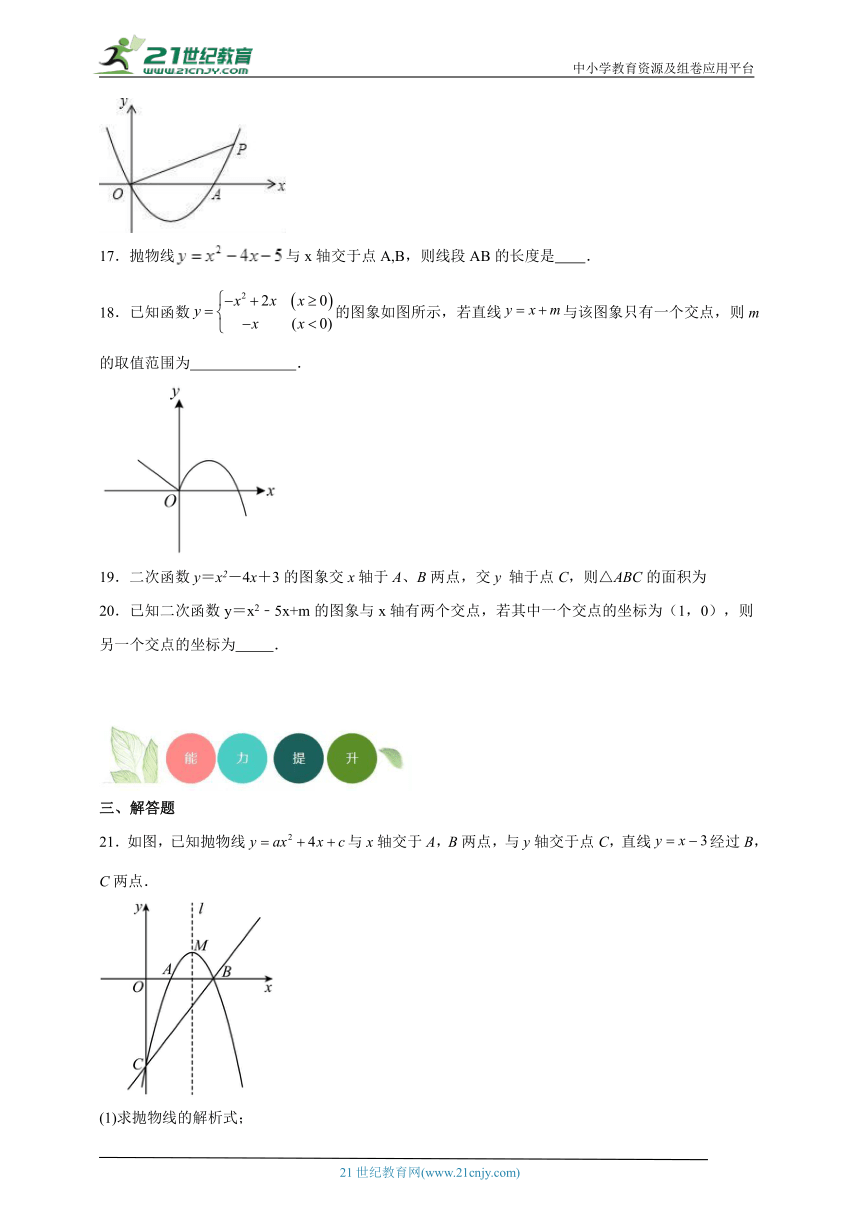
21.如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,直线经过B,C两点.
(1)求抛物线的解析式;
(2)抛物线的顶点为M,在该抛物线的对称轴l上是否存在点P,使得以C,M,P为顶点的三角形是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
22.已知关于的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若m为整数,当此方程有两个互不相等的负整数根时,求m的值;
(3)在(2)的条件下,设抛物线与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=BC,求点P的坐标.
23.在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则称这个点为“美好点”,如图,过点P分别作x轴,y轴的垂线,与坐标轴围成的矩形OAPB的周长与面积相等,则P为“美好点”.
(1)在点M(2,2),N(4,4),Q(﹣6,3)中,是“美好点”的有 ;
(2)若“美好点”P(a,﹣3)在直线y=x+b(b为常数)上,求a和b的值;
(3)若“美好点”P恰好在抛物线第一象限的图象上,在x轴上是否存在一点Q使得△POQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
24.如图,在平面直角坐标系xOy中,直线l:y=kx+m交y轴于点C,与抛物线y=ax2+bx交于点A(4,0)、B(-,-).
(1)直线l的表达式为:______,抛物线的表达式为:______;
(2)若点P是二次函数y=ax2+bx在第四象限内的图象上的一点,且2S△APB=S△AOB,求△AOP的面积;
(3)若点Q是二次函数图象上一点,设点Q到直线l的距离为d,到抛物线的对称轴的距离为d1,当|d-d1|=2时,请直接写出点Q的坐标.
25.已知抛物线y=x2﹣(2k﹣1)x+k2﹣k+1的顶点在坐标轴上,求k的值.
参考答案:
1.D
2.C
3.C
4.B
5.C
6.B
7.C
8.B
9.B
10.A
11.x<-2或x>8
12.2
13.k≤3且k≠2
14.
15.
16./0.5
17.6
18.或
19.3
20.(4,0).
21.(1)
(2)点P的坐标为或或或
22.(1)略;(2)1;(3)或.
23.(1)N、Q;(2)a=6,b=﹣9或a=﹣6,b=3;(3)存在,点Q的坐标为(6,0)或(,0).
24.(1)y=x-3,y=-x2+2x;(2)S△AOP=;(3)点Q的坐标为(,2-3)或(-,-3-2)或(6,-6)或(-1,-)或(1,)或(-4,-16)或(4,0).
25.,2或-1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
30.5二次函数与一元二次方程的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛物线与直线交于两点,若,则关于直线;甲答:一定经过一、四象限,乙答:一定经过一、三象限.则正确的是( )
A.甲乙均错 B.甲乙均对 C.甲错乙对 D.甲对乙错
2.已知二次函数y=x2+bx-2的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是 ( )
A.(3,0) B.(2,0) C.(-2,0) D.(-1,0)
3.观察下列表格,求一元二次方程x2﹣x=1.1的一个近似解是( )
x 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9
x2﹣x 0.11 0.24 0.39 0.56 0.75 0.96 1.19 1.44 1.71
A.0.11 B.1.6 C.1.7 D.1.19
4.定义min{a,b,c}为a,b,c中的最小值,例如:min{5,3,1}=1,min{8,5,5}=5.如果min{4,x2﹣4x,﹣3}=﹣3,那么x的取值范围是( )
A.1≤x≤3 B.x≤1或x≥3 C.1<x<3 D.x<1或x>3
5.如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1,
其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
6.二次函数(,,为常数,且)中的与的部分对应值如下表:
以下结论:
①二次函数有最小值为;
②当时,随的增大而增大;
③二次函数的图象与轴只有一个交点;
④当时,.
其中正确的结论有( )个
A. B. C. D.
7.如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1 . 其中正确的是( )
A.①②③ B.①③⑤ C.①④⑤ D.②③④
8.对于二次函数,下列说法正确的是( )
A.当x>0,y随x的增大而增大 B.当x=2时,y有最大值-3 C.图像的顶点坐标为(-2,-7) D.图像与x轴有两个交点
9.抛物线的对称轴为直线x=1,与x轴的一个交点坐标为(, 0),其部分图象如图所示.下列结论:①;②方程的两个根是;③;④当时,x的取值范围是;⑤m为任意实数,其中结论正确的个数是( )
A.4个 B.3个 C.2个 D.1个
10.若关于的一元二次方程有两个不同的实数根,,方程有两个不同的实数根,,则,,,的大小关系为( )
A.p
11.已知函数y1=(a2+1)x2+bx+c,y2=-x+2,若方程(a2+1)x2+(b+1)x+c-2=0的两根分别为x1=-2,x2=8,则使y1> y2,成立的x的取值范围是 .
12.已知抛物线的对称轴是x=m,若该抛物线与x轴交于(1,0),(3,0)两点,则m的值为
13.若二次函数y=(k﹣2)x2﹣2x+1与x轴有交点,则k的取值范围为 .
14.抛物线与直线的两个交点的横坐标分别是,,记,则代数式的值为 .
15.在平面直角坐标系中,与抛物线关于轴成轴对称的抛物线的解析式是
16.如图,在平面直角坐标系中,抛物线与x轴交于点A,点P在抛物线上,连接.若是以为底边的等腰三角形,则的面积是 .
17.抛物线与x轴交于点A,B,则线段AB的长度是 .
18.已知函数的图象如图所示,若直线与该图象只有一个交点,则m的取值范围为 .
19.二次函数y=x2-4x+3的图象交x轴于A、B两点,交y 轴于点C,则△ABC的面积为
20.已知二次函数y=x2﹣5x+m的图象与x轴有两个交点,若其中一个交点的坐标为(1,0),则另一个交点的坐标为 .
三、解答题
21.如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,直线经过B,C两点.
(1)求抛物线的解析式;
(2)抛物线的顶点为M,在该抛物线的对称轴l上是否存在点P,使得以C,M,P为顶点的三角形是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
22.已知关于的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若m为整数,当此方程有两个互不相等的负整数根时,求m的值;
(3)在(2)的条件下,设抛物线与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=BC,求点P的坐标.
23.在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则称这个点为“美好点”,如图,过点P分别作x轴,y轴的垂线,与坐标轴围成的矩形OAPB的周长与面积相等,则P为“美好点”.
(1)在点M(2,2),N(4,4),Q(﹣6,3)中,是“美好点”的有 ;
(2)若“美好点”P(a,﹣3)在直线y=x+b(b为常数)上,求a和b的值;
(3)若“美好点”P恰好在抛物线第一象限的图象上,在x轴上是否存在一点Q使得△POQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
24.如图,在平面直角坐标系xOy中,直线l:y=kx+m交y轴于点C,与抛物线y=ax2+bx交于点A(4,0)、B(-,-).
(1)直线l的表达式为:______,抛物线的表达式为:______;
(2)若点P是二次函数y=ax2+bx在第四象限内的图象上的一点,且2S△APB=S△AOB,求△AOP的面积;
(3)若点Q是二次函数图象上一点,设点Q到直线l的距离为d,到抛物线的对称轴的距离为d1,当|d-d1|=2时,请直接写出点Q的坐标.
25.已知抛物线y=x2﹣(2k﹣1)x+k2﹣k+1的顶点在坐标轴上,求k的值.
参考答案:
1.D
2.C
3.C
4.B
5.C
6.B
7.C
8.B
9.B
10.A
11.x<-2或x>8
12.2
13.k≤3且k≠2
14.
15.
16./0.5
17.6
18.或
19.3
20.(4,0).
21.(1)
(2)点P的坐标为或或或
22.(1)略;(2)1;(3)或.
23.(1)N、Q;(2)a=6,b=﹣9或a=﹣6,b=3;(3)存在,点Q的坐标为(6,0)或(,0).
24.(1)y=x-3,y=-x2+2x;(2)S△AOP=;(3)点Q的坐标为(,2-3)或(-,-3-2)或(6,-6)或(-1,-)或(1,)或(-4,-16)或(4,0).
25.,2或-1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
