29.5 正多边形与圆课时练(含答案)
文档属性
| 名称 | 29.5 正多边形与圆课时练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 695.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
第二十九章 直线与圆的位置关系
29.5 正多边形与圆
基础过关全练
知识点1 正多边形与圆的关系
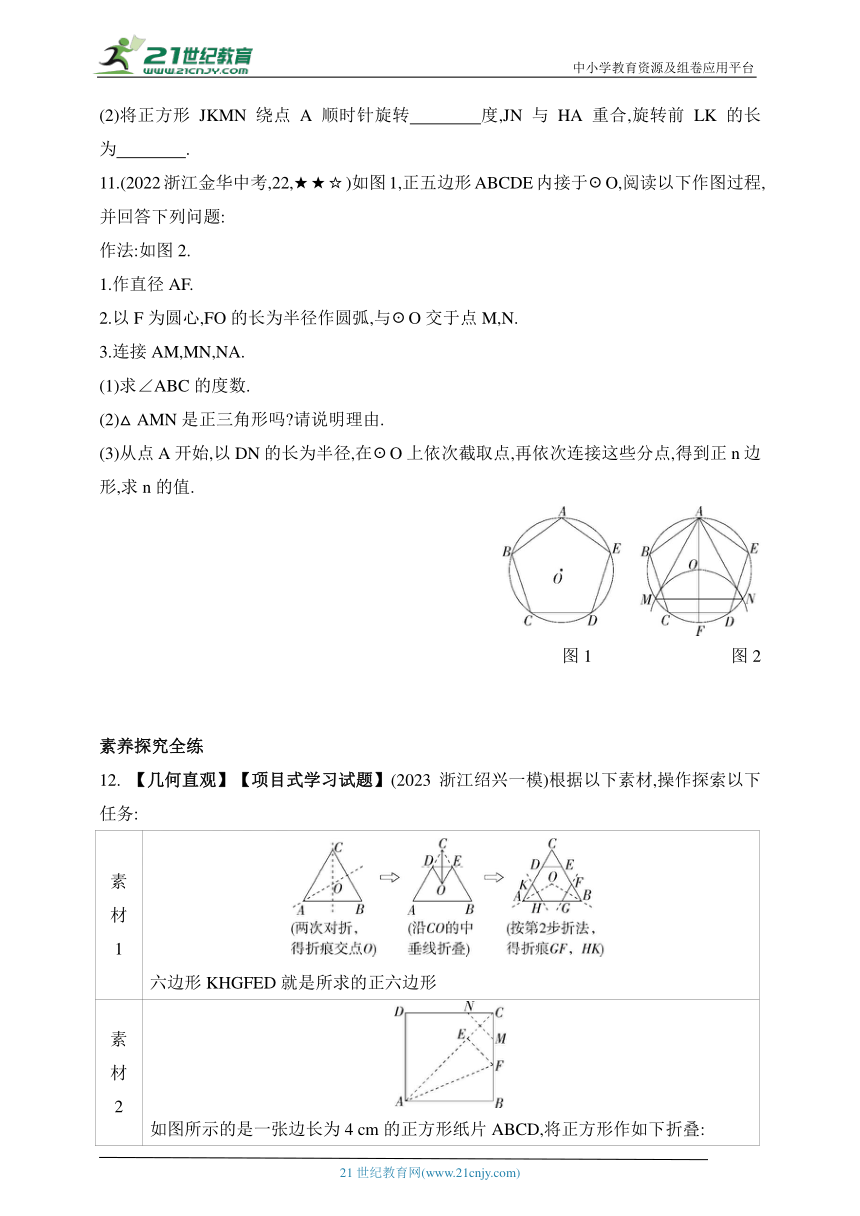
1.【教材变式·P17例2·条件变结论】如图,△ABC为☉O的内接正三角形,如果正三角形的边心距为,求☉O的半径.
知识点2 与正多边形有关的概念和计算
2.【一题多变·正多边形的中心角】如图,☉O的内接正六边形ABCDEF的边长为1,则的长为 ( )
A.π B.π C.π D.π
[变式·改为求圆周角]【新独家原创】如图,正六边形ABCDEF内接于☉O,点M在上,则∠BME的度数为 ( )
A.72° B.45° C.60° D.90°
3.【中华优秀传统文化】在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受到了中国人的浪漫.如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3),则顶点C的坐标为 ( )
A.(2-2,3) B.(0,1+2)
C.(2-,3) D.(2-2,2+)
4.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角= ,边长= ,边心距= .
5.已知正五边形ABCDE,请仅用无刻度的直尺作图.
(1)在图1中作点P,使得△BDP是等腰三角形;
(2)在图2中作点O,使点O为正五边形ABCDE的中心.
图1 图2
知识点3 正多边形的画法
6.如图,在网格纸中,O、A都是格点,以O为圆心,OA为半径作圆,用无刻度的直尺完成以下画图:画圆O的一个内接正六边形ABCDEF.
能力提升全练
7.(2022四川成都中考,6,★☆☆)如图,正六边形ABCDEF内接于☉O,若☉O的周长等于6π,则正六边形的边长为 ( )
A. B. C.3 D.2
8.(2023河北石家庄桥西质检,13,★☆☆)如图所示,正五边形ABCDE的顶点A,B在射线OM上,顶点E在射线ON上,∠AEO=2∠DEN,则∠O的度数为 ( )
A.80° B.72° C.60° D.50°
9.(2023河北衡水二模,6,★★☆)如图,BD,DF是正六边形ABCDEF的两条对角线,已知四边形ABDF的面积为8,则阴影部分的面积为 ( )
A.2 B.4 C.2 D.3
10.【新考法】(2023河北石家庄四十四中模拟,19,★★☆)如图1,将一个正方形纸片沿虚线对折两次,得到图2,按照图2所示剪去一个腰长为2的等腰直角三角形,展开后得到一个如图3所示的正八边形ABCDEFGH,将剪下的四个等腰直角三角形拼成一个正方形JKMN,放在正八边形内部,MN与BA重合,L为EF的中点,连接LK.
(1)正方形JKMN的边长为 ;
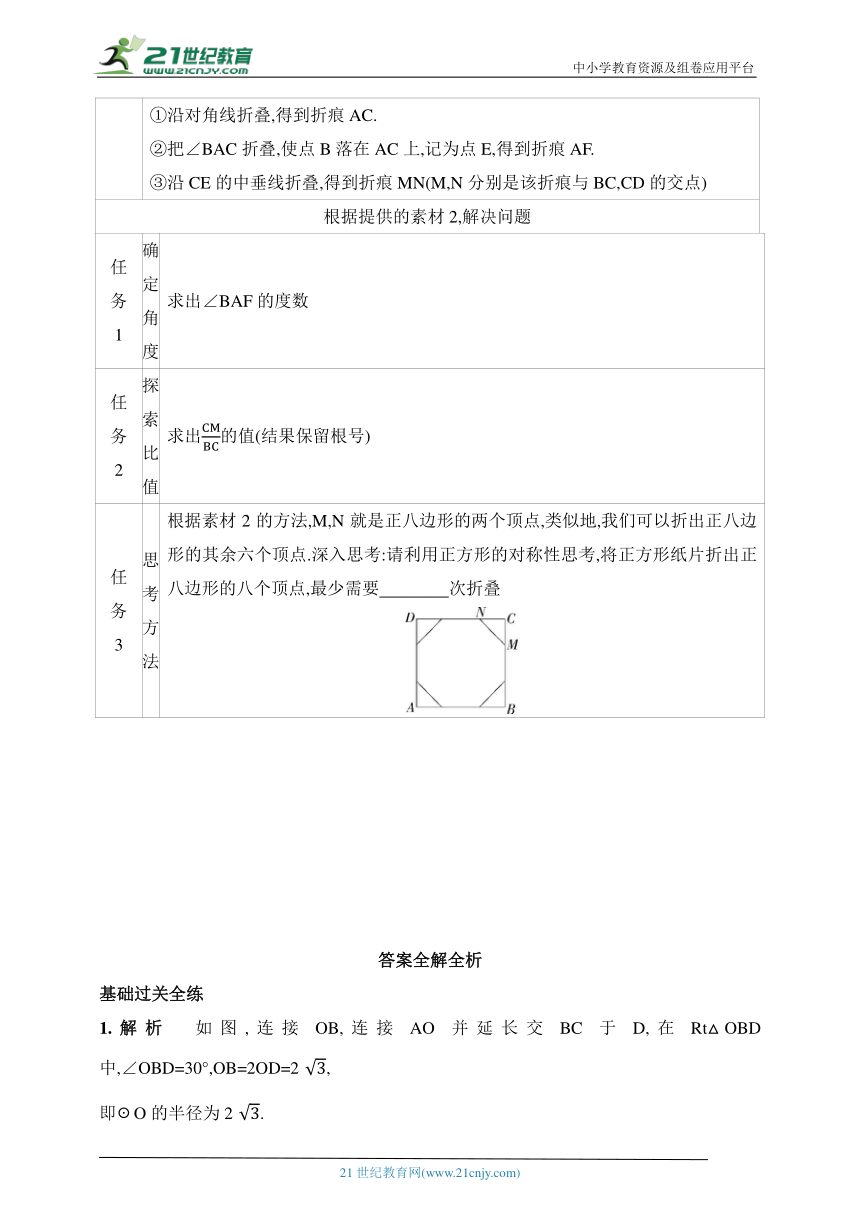
(2)将正方形JKMN绕点A顺时针旋转 度,JN与HA重合,旋转前LK的长为 .
11.(2022浙江金华中考,22,★★☆)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:
作法:如图2.
1.作直径AF.
2.以F为圆心,FO的长为半径作圆弧,与☉O交于点M,N.
3.连接AM,MN,NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN的长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
素养探究全练
12. 【几何直观】【项目式学习试题】(2023浙江绍兴一模)根据以下素材,操作探索以下任务:
素 材 1 六边形KHGFED就是所求的正六边形
素 材 2 如图所示的是一张边长为4 cm的正方形纸片ABCD,将正方形作如下折叠: ①沿对角线折叠,得到折痕AC. ②把∠BAC折叠,使点B落在AC上,记为点E,得到折痕AF. ③沿CE的中垂线折叠,得到折痕MN(M,N分别是该折痕与BC,CD的交点)
根据提供的素材2,解决问题
任 务 1 确定角度 求出∠BAF的度数
任 务 2 探索比值 求出的值(结果保留根号)
任 务 3 思 考 方 法 根据素材2的方法,M,N就是正八边形的两个顶点,类似地,我们可以折出正八边形的其余六个顶点.深入思考:请利用正方形的对称性思考,将正方形纸片折出正八边形的八个顶点,最少需要 次折叠
答案全解全析
基础过关全练
1.解析 如图,连接OB,连接AO并延长交BC于D,在Rt△OBD中,∠OBD=30°,OB=2OD=2,
即☉O的半径为2.
2.B 连接OB、OC(图略),由题意得BC=1,
∵正六边形ABCDEF是☉O的内接正六边形,
∴中心角∠BOC==60°,又∵OB=OC,
∴△BOC是等边三角形,∴OB=OC=BC=1,
则的长为=π,故选B.
[变式] D 连接OB,OC,OD,OE,如图,
∵多边形ABCDEF是正六边形,
∴∠BOC=∠COD=∠DOE=60°,∴∠BOE=3∠COD=180°,
∴∠BME=∠BOE=90°.
3.A 如图,连接BD,CF,BD与CF交于点M,易得点B(2,1),
在Rt△BCM中,BC=4,∠BCM=×120°=60°,∴CM=BC=2,BM=BC=2,∴点C的横坐标为2-2,纵坐标为1+2=3,∴点C的坐标为(2-2,3),故选A.
4. 60°;4;2
解析 在圆内接正六边形ABCDEF中,∠COD==60°,∵OC=OD,∴△OCD是等边三角形,
∴BC=CD=OC=4.∵OG⊥BC,∴CG=BC=2,∵∠COG=∠COD=30°,∴OG=CG=2.
故答案为60°;4;2.
5.解析 (1)如图所示,点P即为所求.(提示:利用正五边形的对称性,直线CP上的点均符合(CP与BD的交点除外),答案不唯一)
(2)如图所示,点O即为所求.(提示:利用正五边形的性质,得到其两条对称轴,进而得出其中心点O的位置)
6.解析 设AO的延长线与圆O交于点D,根据圆的内接正六边形的性质,点D即为所求作的正六边形的一个顶点,且该正六边形的边长等于圆O的半径,故AO的垂直平分线与圆O的交点即为正六边形的顶点B和F.同理,OD的垂直平分线与圆O的交点即为正六边形的顶点C和E,连接AB、BC、CD、DE、EF、FA,如图,正六边形ABCDEF即为所求.
能力提升全练
7.C 连接OB,OC(图略),∵☉O的周长等于6π,∴☉O的半径为3,∵∠BOC=×360°=60°,OB=OC,∴△OBC是等边三角形,∴BC=OB=3,∴正六边形ABCDEF的边长为3,故选C.
8.C ∵五边形ABCDE是正五边形,
∴∠AED=∠EAB==108°,
∵∠AEO=2∠DEN,∠DEN+∠AED+∠AEO=180°,
∴3∠DEN+108°=180°,∴∠DEN=24°,则∠AEO=2∠DEN=48°.∵∠EAB=∠O+∠AEO,∴∠O=∠EAB-∠AEO=108°-48°=60°,故选C.
9.B 连接AD,过点B作BG⊥AD于点G,过点C作CH⊥AD于点H,如图所示,
正六边形每个内角的度数为=120°,
∴∠BAF=∠CDE=120°,
∵正六边形ABCDEF关于直线AD对称,
∴∠BAD=∠CDA=×120°=60°,
∵BG⊥AD,CH⊥AD,
∴∠AGB=∠CHD=90°,∴∠ABG=∠DCH=90°-60°=30°,∴AG=DH=AB=CD,
∵∠ABC+∠BAD=120°+60°=180°,
∴BC∥AD,∴∠GBC=180°-90°=90°,∴∠GBC=∠BGH=∠GHC=90°,∴四边形BCHG是矩形,
∴GH=BC,BG=CH,∴AD=AG+GH+DH=2BC,
∴===,
根据对称性可知S△AFD=S△ABD,S△DEF=S△BCD,
∴S阴影=S△DEF+S△BCD=S△ABD+S△ADF=S四边形ABDF=4.故选B.
10.(1)2 (2)45;3
解析 本题综合考查了折叠、旋转与正八边形的性质.
(1)设正方形JKMN的中心为O,由题意得OA=OB=2,∴正方形JKMN的边长MN==2.
(2)连接AD,BE,如图,
正八边形的内角∠HAB==135°,正方形的内角∠JAB=∠ABK=90°,
∴∠HAJ=135°-90°=45°,即将正方形JKMN绕点A顺时针旋转45度,JN与HA重合.
同理∠KBC=45°,∴∠KBC+∠BCD=180°,∴BK∥CD,由正八边形的性质知BE∥CD,
∴B、K、E在同一直线上,同理A、K、D也在同一直线上,∴四边形BCDK是平行四边形,
∵BK=AB=BC,∴四边形BCDK是菱形,∴DK=BK=DE=2,∠KDC=∠KBC=45°,
∴∠KDE=90°,∴△DKE是等腰直角三角形,
∴KE==4,∠KEL=135°-45°=90°,∵L为EF的中点,∴EL=EF=,
∴KL==3.
11.解析 (1)五边形的内角和为(5-2)×180°=540°,∵五边形ABCDE是正五边形,正五边形的五个内角都相等,∴∠ABC==108°.
(2)△AMN是正三角形,理由如下:
如图,连接ON,FN,由作图知FN=FO,∵ON=OF,
∴ON=OF=FN,∴△OFN是正三角形,∴∠OFN=60°,∴∠AMN=∠OFN=60°,同理∠ANM=60°,
∴△AMN是正三角形.
(3)如图,连接OD,
由(2)知∠AMN=60°,
∴∠AON=2∠AMN=120°.∵=2,∴∠AOD=2×=144°,∵=-,∴∠NOD=144°-120°=24°,∴n==15.
素养探究全练
12.解析 任务1:∵四边形ABCD是正方形,且AC是对角线,∴∠BAC=45°.∵点B,E关于直线AF对称,∴∠BAF=∠BAC=22.5°.
任务2:连接EM,EN,如图,
∵四边形ABCD是正方形,且AC是对角线,
∴∠BCA=∠DCA=45°,
∵点E,C关于直线MN对称,
∴ME=MC,NE=NC,MN垂直平分EC,∴∠CON=∠COM=90°,
∴∠CNM=∠CMN=45°,
∴CM=CN,∴ME=MC=NC=NE.又∵∠DCB=90°,∴四边形MCNE是正方形.
∵AB=AE=4,∴AC=4,∴CE=4-4,∴CM==4-2.∴==.
任务3:素材2已经进行了3次折叠,得到两个顶点,要找出其他6个顶点,根据对称性知至少还需要进行2次折叠,故至少需要5次折叠.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
第二十九章 直线与圆的位置关系
29.5 正多边形与圆
基础过关全练
知识点1 正多边形与圆的关系
1.【教材变式·P17例2·条件变结论】如图,△ABC为☉O的内接正三角形,如果正三角形的边心距为,求☉O的半径.
知识点2 与正多边形有关的概念和计算
2.【一题多变·正多边形的中心角】如图,☉O的内接正六边形ABCDEF的边长为1,则的长为 ( )
A.π B.π C.π D.π
[变式·改为求圆周角]【新独家原创】如图,正六边形ABCDEF内接于☉O,点M在上,则∠BME的度数为 ( )
A.72° B.45° C.60° D.90°
3.【中华优秀传统文化】在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受到了中国人的浪漫.如图,将“雪花”图案(边长为4的正六边形ABCDEF)放在平面直角坐标系中,若AB与x轴垂直,顶点A的坐标为(2,-3),则顶点C的坐标为 ( )
A.(2-2,3) B.(0,1+2)
C.(2-,3) D.(2-2,2+)
4.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角= ,边长= ,边心距= .
5.已知正五边形ABCDE,请仅用无刻度的直尺作图.
(1)在图1中作点P,使得△BDP是等腰三角形;
(2)在图2中作点O,使点O为正五边形ABCDE的中心.
图1 图2
知识点3 正多边形的画法
6.如图,在网格纸中,O、A都是格点,以O为圆心,OA为半径作圆,用无刻度的直尺完成以下画图:画圆O的一个内接正六边形ABCDEF.
能力提升全练
7.(2022四川成都中考,6,★☆☆)如图,正六边形ABCDEF内接于☉O,若☉O的周长等于6π,则正六边形的边长为 ( )
A. B. C.3 D.2
8.(2023河北石家庄桥西质检,13,★☆☆)如图所示,正五边形ABCDE的顶点A,B在射线OM上,顶点E在射线ON上,∠AEO=2∠DEN,则∠O的度数为 ( )
A.80° B.72° C.60° D.50°
9.(2023河北衡水二模,6,★★☆)如图,BD,DF是正六边形ABCDEF的两条对角线,已知四边形ABDF的面积为8,则阴影部分的面积为 ( )
A.2 B.4 C.2 D.3
10.【新考法】(2023河北石家庄四十四中模拟,19,★★☆)如图1,将一个正方形纸片沿虚线对折两次,得到图2,按照图2所示剪去一个腰长为2的等腰直角三角形,展开后得到一个如图3所示的正八边形ABCDEFGH,将剪下的四个等腰直角三角形拼成一个正方形JKMN,放在正八边形内部,MN与BA重合,L为EF的中点,连接LK.
(1)正方形JKMN的边长为 ;
(2)将正方形JKMN绕点A顺时针旋转 度,JN与HA重合,旋转前LK的长为 .
11.(2022浙江金华中考,22,★★☆)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:
作法:如图2.
1.作直径AF.
2.以F为圆心,FO的长为半径作圆弧,与☉O交于点M,N.
3.连接AM,MN,NA.
(1)求∠ABC的度数.
(2)△AMN是正三角形吗 请说明理由.
(3)从点A开始,以DN的长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
素养探究全练
12. 【几何直观】【项目式学习试题】(2023浙江绍兴一模)根据以下素材,操作探索以下任务:
素 材 1 六边形KHGFED就是所求的正六边形
素 材 2 如图所示的是一张边长为4 cm的正方形纸片ABCD,将正方形作如下折叠: ①沿对角线折叠,得到折痕AC. ②把∠BAC折叠,使点B落在AC上,记为点E,得到折痕AF. ③沿CE的中垂线折叠,得到折痕MN(M,N分别是该折痕与BC,CD的交点)
根据提供的素材2,解决问题
任 务 1 确定角度 求出∠BAF的度数
任 务 2 探索比值 求出的值(结果保留根号)
任 务 3 思 考 方 法 根据素材2的方法,M,N就是正八边形的两个顶点,类似地,我们可以折出正八边形的其余六个顶点.深入思考:请利用正方形的对称性思考,将正方形纸片折出正八边形的八个顶点,最少需要 次折叠
答案全解全析
基础过关全练
1.解析 如图,连接OB,连接AO并延长交BC于D,在Rt△OBD中,∠OBD=30°,OB=2OD=2,
即☉O的半径为2.
2.B 连接OB、OC(图略),由题意得BC=1,
∵正六边形ABCDEF是☉O的内接正六边形,
∴中心角∠BOC==60°,又∵OB=OC,
∴△BOC是等边三角形,∴OB=OC=BC=1,
则的长为=π,故选B.
[变式] D 连接OB,OC,OD,OE,如图,
∵多边形ABCDEF是正六边形,
∴∠BOC=∠COD=∠DOE=60°,∴∠BOE=3∠COD=180°,
∴∠BME=∠BOE=90°.
3.A 如图,连接BD,CF,BD与CF交于点M,易得点B(2,1),
在Rt△BCM中,BC=4,∠BCM=×120°=60°,∴CM=BC=2,BM=BC=2,∴点C的横坐标为2-2,纵坐标为1+2=3,∴点C的坐标为(2-2,3),故选A.
4. 60°;4;2
解析 在圆内接正六边形ABCDEF中,∠COD==60°,∵OC=OD,∴△OCD是等边三角形,
∴BC=CD=OC=4.∵OG⊥BC,∴CG=BC=2,∵∠COG=∠COD=30°,∴OG=CG=2.
故答案为60°;4;2.
5.解析 (1)如图所示,点P即为所求.(提示:利用正五边形的对称性,直线CP上的点均符合(CP与BD的交点除外),答案不唯一)
(2)如图所示,点O即为所求.(提示:利用正五边形的性质,得到其两条对称轴,进而得出其中心点O的位置)
6.解析 设AO的延长线与圆O交于点D,根据圆的内接正六边形的性质,点D即为所求作的正六边形的一个顶点,且该正六边形的边长等于圆O的半径,故AO的垂直平分线与圆O的交点即为正六边形的顶点B和F.同理,OD的垂直平分线与圆O的交点即为正六边形的顶点C和E,连接AB、BC、CD、DE、EF、FA,如图,正六边形ABCDEF即为所求.
能力提升全练
7.C 连接OB,OC(图略),∵☉O的周长等于6π,∴☉O的半径为3,∵∠BOC=×360°=60°,OB=OC,∴△OBC是等边三角形,∴BC=OB=3,∴正六边形ABCDEF的边长为3,故选C.
8.C ∵五边形ABCDE是正五边形,
∴∠AED=∠EAB==108°,
∵∠AEO=2∠DEN,∠DEN+∠AED+∠AEO=180°,
∴3∠DEN+108°=180°,∴∠DEN=24°,则∠AEO=2∠DEN=48°.∵∠EAB=∠O+∠AEO,∴∠O=∠EAB-∠AEO=108°-48°=60°,故选C.
9.B 连接AD,过点B作BG⊥AD于点G,过点C作CH⊥AD于点H,如图所示,
正六边形每个内角的度数为=120°,
∴∠BAF=∠CDE=120°,
∵正六边形ABCDEF关于直线AD对称,
∴∠BAD=∠CDA=×120°=60°,
∵BG⊥AD,CH⊥AD,
∴∠AGB=∠CHD=90°,∴∠ABG=∠DCH=90°-60°=30°,∴AG=DH=AB=CD,
∵∠ABC+∠BAD=120°+60°=180°,
∴BC∥AD,∴∠GBC=180°-90°=90°,∴∠GBC=∠BGH=∠GHC=90°,∴四边形BCHG是矩形,
∴GH=BC,BG=CH,∴AD=AG+GH+DH=2BC,
∴===,
根据对称性可知S△AFD=S△ABD,S△DEF=S△BCD,
∴S阴影=S△DEF+S△BCD=S△ABD+S△ADF=S四边形ABDF=4.故选B.
10.(1)2 (2)45;3
解析 本题综合考查了折叠、旋转与正八边形的性质.
(1)设正方形JKMN的中心为O,由题意得OA=OB=2,∴正方形JKMN的边长MN==2.
(2)连接AD,BE,如图,
正八边形的内角∠HAB==135°,正方形的内角∠JAB=∠ABK=90°,
∴∠HAJ=135°-90°=45°,即将正方形JKMN绕点A顺时针旋转45度,JN与HA重合.
同理∠KBC=45°,∴∠KBC+∠BCD=180°,∴BK∥CD,由正八边形的性质知BE∥CD,
∴B、K、E在同一直线上,同理A、K、D也在同一直线上,∴四边形BCDK是平行四边形,
∵BK=AB=BC,∴四边形BCDK是菱形,∴DK=BK=DE=2,∠KDC=∠KBC=45°,
∴∠KDE=90°,∴△DKE是等腰直角三角形,
∴KE==4,∠KEL=135°-45°=90°,∵L为EF的中点,∴EL=EF=,
∴KL==3.
11.解析 (1)五边形的内角和为(5-2)×180°=540°,∵五边形ABCDE是正五边形,正五边形的五个内角都相等,∴∠ABC==108°.
(2)△AMN是正三角形,理由如下:
如图,连接ON,FN,由作图知FN=FO,∵ON=OF,
∴ON=OF=FN,∴△OFN是正三角形,∴∠OFN=60°,∴∠AMN=∠OFN=60°,同理∠ANM=60°,
∴△AMN是正三角形.
(3)如图,连接OD,
由(2)知∠AMN=60°,
∴∠AON=2∠AMN=120°.∵=2,∴∠AOD=2×=144°,∵=-,∴∠NOD=144°-120°=24°,∴n==15.
素养探究全练
12.解析 任务1:∵四边形ABCD是正方形,且AC是对角线,∴∠BAC=45°.∵点B,E关于直线AF对称,∴∠BAF=∠BAC=22.5°.
任务2:连接EM,EN,如图,
∵四边形ABCD是正方形,且AC是对角线,
∴∠BCA=∠DCA=45°,
∵点E,C关于直线MN对称,
∴ME=MC,NE=NC,MN垂直平分EC,∴∠CON=∠COM=90°,
∴∠CNM=∠CMN=45°,
∴CM=CN,∴ME=MC=NC=NE.又∵∠DCB=90°,∴四边形MCNE是正方形.
∵AB=AE=4,∴AC=4,∴CE=4-4,∴CM==4-2.∴==.
任务3:素材2已经进行了3次折叠,得到两个顶点,要找出其他6个顶点,根据对称性知至少还需要进行2次折叠,故至少需要5次折叠.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
