32.3 直棱柱和圆锥的侧面展开图课时练(含解析)
文档属性
| 名称 | 32.3 直棱柱和圆锥的侧面展开图课时练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 519.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 17:48:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
第三十二章 投影与视图
32.3 直棱柱和圆锥的侧面展开图
基础过关全练
知识点1 棱柱的展开图
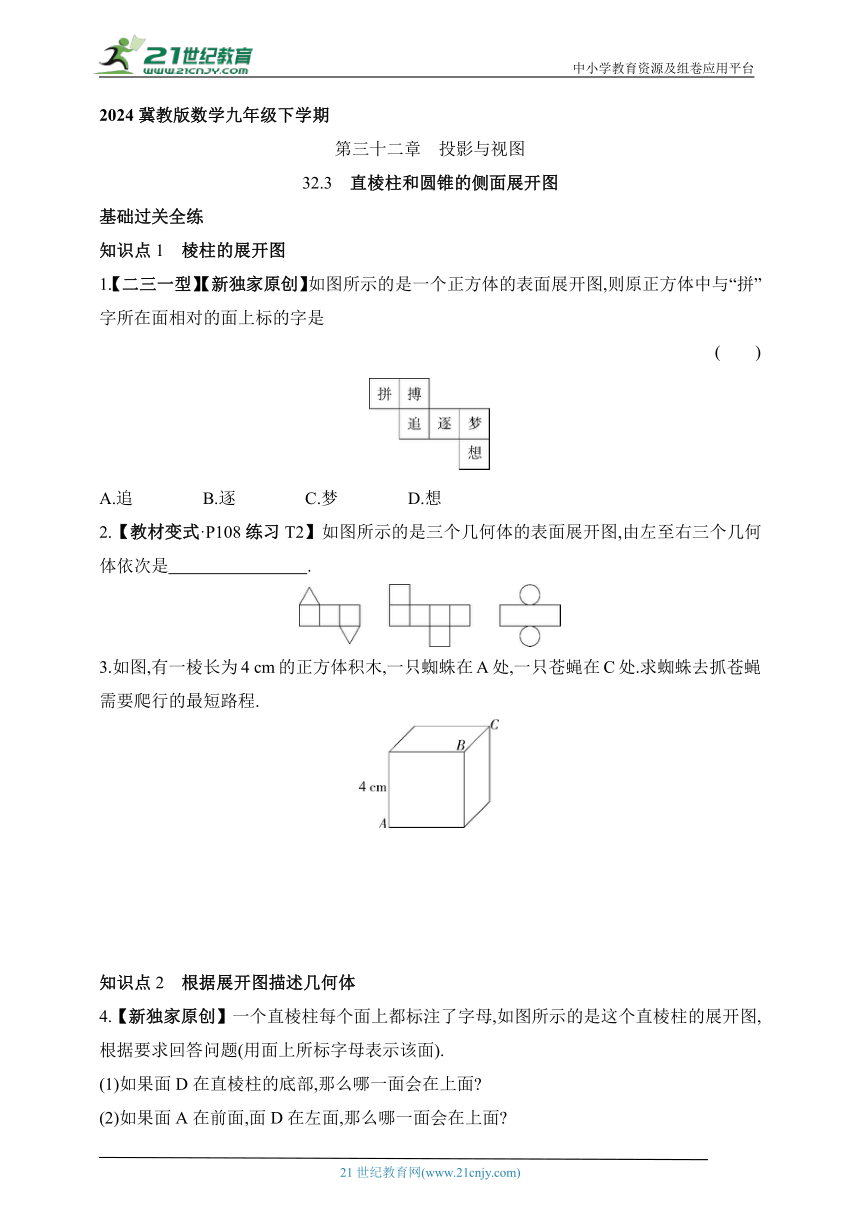
1.【二三一型】【新独家原创】如图所示的是一个正方体的表面展开图,则原正方体中与“拼”字所在面相对的面上标的字是
( )
A.追 B.逐 C.梦 D.想
2.【教材变式·P108练习T2】如图所示的是三个几何体的表面展开图,由左至右三个几何体依次是 .
3.如图,有一棱长为4 cm的正方体积木,一只蜘蛛在A处,一只苍蝇在C处.求蜘蛛去抓苍蝇需要爬行的最短路程.
知识点2 根据展开图描述几何体
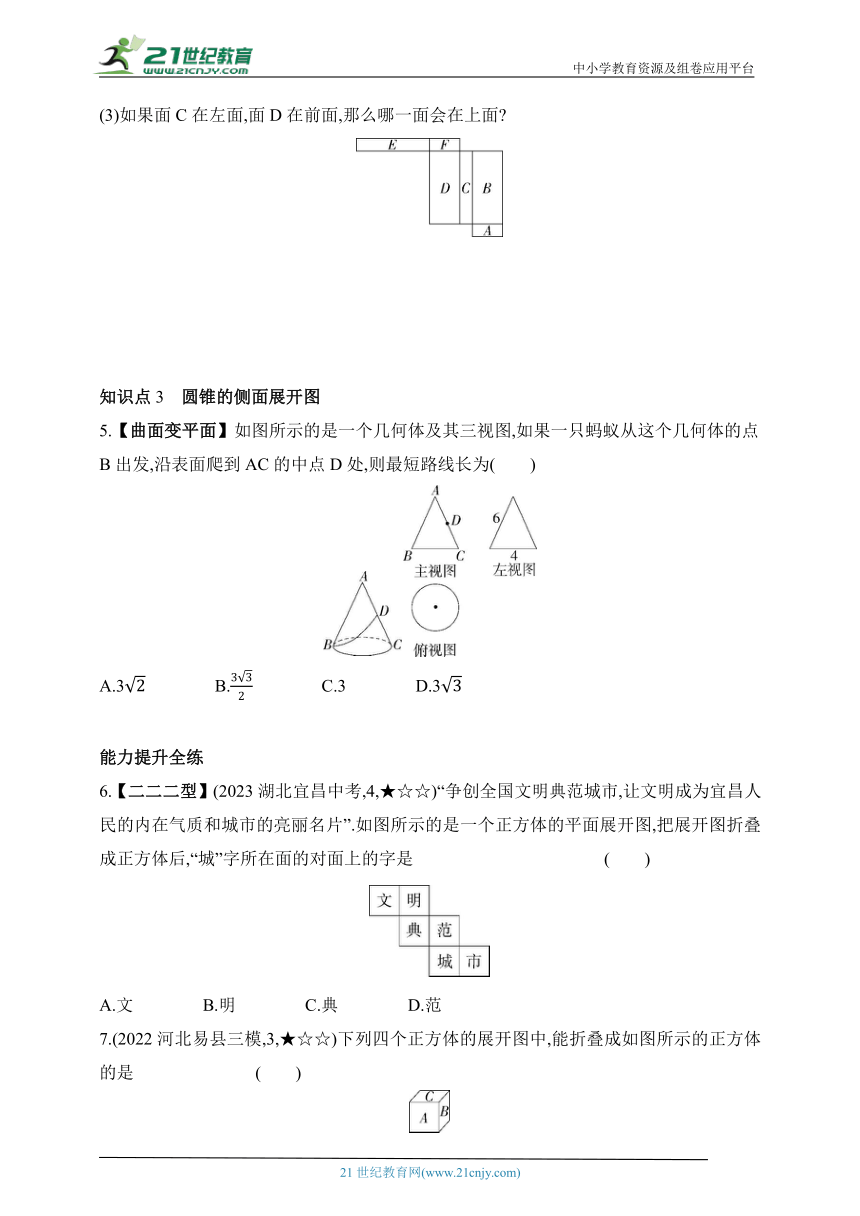
4.【新独家原创】一个直棱柱每个面上都标注了字母,如图所示的是这个直棱柱的展开图,根据要求回答问题(用面上所标字母表示该面).
(1)如果面D在直棱柱的底部,那么哪一面会在上面
(2)如果面A在前面,面D在左面,那么哪一面会在上面
(3)如果面C在左面,面D在前面,那么哪一面会在上面
知识点3 圆锥的侧面展开图
5.【曲面变平面】如图所示的是一个几何体及其三视图,如果一只蚂蚁从这个几何体的点B出发,沿表面爬到AC的中点D处,则最短路线长为( )
A.3 B. C.3 D.3
能力提升全练
6.【二二二型】(2023湖北宜昌中考,4,★☆☆)“争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图所示的是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字所在面的对面上的字是 ( )
A.文 B.明 C.典 D.范
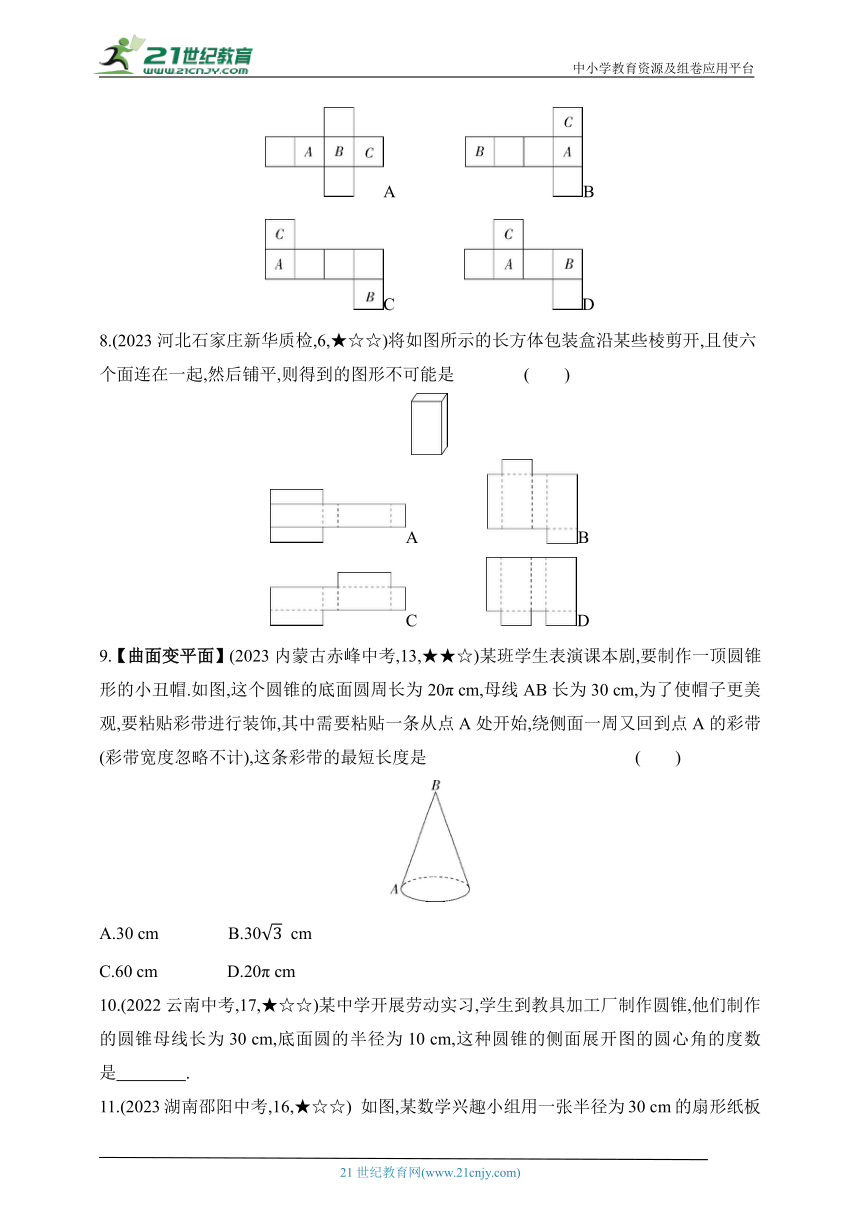
7.(2022河北易县三模,3,★☆☆)下列四个正方体的展开图中,能折叠成如图所示的正方体的是 ( )
A B
C D
8.(2023河北石家庄新华质检,6,★☆☆)将如图所示的长方体包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形不可能是 ( )
A B
C D
9.【曲面变平面】(2023内蒙古赤峰中考,13,★★☆)某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为20π cm,母线AB长为30 cm,为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是 ( )
A.30 cm B.30 cm
C.60 cm D.20π cm
10.(2022云南中考,17,★☆☆)某中学开展劳动实习,学生到教具加工厂制作圆锥,他们制作的圆锥母线长为30 cm,底面圆的半径为10 cm,这种圆锥的侧面展开图的圆心角的度数是 .
11.(2023湖南邵阳中考,16,★☆☆) 如图,某数学兴趣小组用一张半径为30 cm的扇形纸板做成一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为8 cm,那么这张扇形纸板的面积为 cm2.(结果保留π)
12.(2023河北石家庄长安质检,18,★☆☆)如图1,冰激凌的外壳(不计厚度)可近似看做圆锥,其母线长为12 cm,底面圆直径为8 cm.
(1)这个冰激凌外壳的侧面展开图的形状是 ;
(2)当冰激凌被吃掉一部分后,其外壳仍可近似看做圆锥,如图2,其母线长为9 cm,则此时冰激凌外壳的侧面积为 cm2.(结果保留π)
素养探究全练
13.【空间观念】【新考向·阅读理解题】研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.
(1)【阅读材料】
立体图形中既不相交也不平行的两条直线所成的角,就是将一条直线平移使其与另一条直线相交所成的角.
例如,正方体ABCD-A'B'C'D'(图1),因为在平面AA'C'C中,CC'∥AA',AA'与AB相交于点A,所以直线AB与AA'所成的∠BAA'就是既不相交也不平行的两条直线AB与CC'所成的角.
【解决问题】
如图1,已知正方体ABCD-A'B'C'D',求既不相交也不平行的两条直线BA'与AC所成角的大小.
(2)如图2,M,N是正方体相邻两个面上的点.
①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是 .
②在所选正确展开图中,若点M到AB,BC的距离分别是2和5,点N到BD,BC的距离分别是4和3,一只蚂蚁从M点出发,经过线段AB上的某点P,沿正方体表面爬行到N点,则蚂蚁爬行的最短路程是多少
答案全解全析
基础过关全练
1.B 动手操作一下,知拼字所在面与逐字所在面相对,故选B.
2.三棱柱、正方体、圆柱
解析 从题图中三个表面展开图的特征可得由左至右三个几何体依次是三棱柱、正方体、圆柱.
3. 解析 将这个正方体积木的表面展开如图:
连接AC,根据“两点之间线段最短”,可知AC的长就是蜘蛛去抓苍蝇需要爬行的最短路程.
在Rt△ACD中,AC===4(cm).
答:蜘蛛去抓苍蝇需要爬行的最短路程是4 cm.
4.解析 由平面图形的折叠及棱柱的展开图的特征可知,这个几何体是直四棱柱,面A与面F相对,面B与面D相对,面C与面E相对.
(1)如果面D在直棱柱的底部,那么面B会在上面.
(2)如果面A在前面,面D在左面,那么面C会在上面.
(3)如果面C在左面,面D在前面,那么面A会在上面.
5.D 易知该几何体是圆锥,圆锥的侧面展开图如图,连接BD、BC,BD的长即为最短路线长.
设侧面展开图的扇形圆心角为n°,∵扇形弧长=底面圆周长,∴4π=,∴n=120,∴∠BAC=60°,∵AB=AC,∴△ABC是等边三角形,∵D为AC的中点,∴BD⊥AC,AD=AC=3.由勾股定理得BD2=AB2-AD2=27,∴BD=3.故选D.
能力提升全练
6.B 正方体的表面展开图,相对的面之间一定相隔一个正方形,易知“城”字所在面与“明”字所在面相对,故选B.
7.B 由题意可得正方体中面A,面B,面C为相邻面,
由A选项中的展开图可得面A,面C为相对面,故选项A不符合题意;由B选项中的展开图可得面A,面B,面C为相邻面,故选项B符合题意;由C选项中的展开图可得面B,面C为相对面,故选项C不符合题意;由D选项中的展开图可得面A,面B为相对面,故选项D不符合题意.故选B.
8.D D选项中有一对相对面在同一侧,不是长方体的展开图,故此选项符合题意.故选D.
9.B 圆锥的侧面展开图如图所示,AC即为所求,过点B作BD⊥AC于点D,
∵=20π,∴n=120,∴侧面展开图的圆心角为120°.∵∠ABC=120°,BA=BC,∴∠BAC=30°,∴BD=AB=15 cm,
∴AD==15 cm,∴AC=2AD=30 cm,
故彩带的最短长度为30 cm.
方法解读 曲面变平面:利用了转化思想,由几何体通过空间想象得到侧面展开图,构造直角三角形,结合勾股定理求最值.
10.120°
解析 设这种圆锥的侧面展开图的圆心角的度数为n°,则=2×π×10,解得n=120,故答案为120°.
11.240π
解析 帽子底面圆周长为2×8π=16π(cm),即扇形弧长为16π cm,故扇形面积为lr=×16π×30=240π(cm2).故答案为240π.
12.(1)扇形 (2)27π
解析 (1)由圆锥的性质可知其侧面展开图是扇形.
(2)设题图1中圆锥的侧面展开图对应扇形的圆心角的度数为n°,则8π=,解得n=120.
题图2中圆锥的母线长为9 cm,此时冰激凌外壳的侧面积为=27π(cm2).
素养探究全练
13.解析 (1)连接BC',
∵AC∥A'C',BA'与A'C'相交于点A',∴既不相交也不平行的两条直线BA'与AC所成角为∠BA'C',根据正方体性质可得A'B=BC'=A'C',∴△A'BC'为等边三角形,∴∠BA'C'=60°,∴既不相交也不平行的两条直线BA'与AC所成角为60°.
(2)①根据正方体展开图可以判断,题图甲与原图形中对应点位置不符,题图乙不能拼成正方体,故答案为丙.
②如图,作M关于直线AB的对称点M',
连接NM',与AB交于点P,连接MP,则PM+PN=PM'+PN=NM',此时爬行的路程最短.过点N作BC垂线,并延长与直线M'M交于点E,
∵点M到BC的距离是5,点N到BC的距离是3,
∴NE=8,∵点M到AB的距离是2,点N到BD的距离是4,∴EM'=6,∴NM'===10,故蚂蚁爬行的最短路程为10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
第三十二章 投影与视图
32.3 直棱柱和圆锥的侧面展开图
基础过关全练
知识点1 棱柱的展开图
1.【二三一型】【新独家原创】如图所示的是一个正方体的表面展开图,则原正方体中与“拼”字所在面相对的面上标的字是
( )
A.追 B.逐 C.梦 D.想
2.【教材变式·P108练习T2】如图所示的是三个几何体的表面展开图,由左至右三个几何体依次是 .
3.如图,有一棱长为4 cm的正方体积木,一只蜘蛛在A处,一只苍蝇在C处.求蜘蛛去抓苍蝇需要爬行的最短路程.
知识点2 根据展开图描述几何体
4.【新独家原创】一个直棱柱每个面上都标注了字母,如图所示的是这个直棱柱的展开图,根据要求回答问题(用面上所标字母表示该面).
(1)如果面D在直棱柱的底部,那么哪一面会在上面
(2)如果面A在前面,面D在左面,那么哪一面会在上面
(3)如果面C在左面,面D在前面,那么哪一面会在上面
知识点3 圆锥的侧面展开图
5.【曲面变平面】如图所示的是一个几何体及其三视图,如果一只蚂蚁从这个几何体的点B出发,沿表面爬到AC的中点D处,则最短路线长为( )
A.3 B. C.3 D.3
能力提升全练
6.【二二二型】(2023湖北宜昌中考,4,★☆☆)“争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图所示的是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字所在面的对面上的字是 ( )
A.文 B.明 C.典 D.范
7.(2022河北易县三模,3,★☆☆)下列四个正方体的展开图中,能折叠成如图所示的正方体的是 ( )
A B
C D
8.(2023河北石家庄新华质检,6,★☆☆)将如图所示的长方体包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形不可能是 ( )
A B
C D
9.【曲面变平面】(2023内蒙古赤峰中考,13,★★☆)某班学生表演课本剧,要制作一顶圆锥形的小丑帽.如图,这个圆锥的底面圆周长为20π cm,母线AB长为30 cm,为了使帽子更美观,要粘贴彩带进行装饰,其中需要粘贴一条从点A处开始,绕侧面一周又回到点A的彩带(彩带宽度忽略不计),这条彩带的最短长度是 ( )
A.30 cm B.30 cm
C.60 cm D.20π cm
10.(2022云南中考,17,★☆☆)某中学开展劳动实习,学生到教具加工厂制作圆锥,他们制作的圆锥母线长为30 cm,底面圆的半径为10 cm,这种圆锥的侧面展开图的圆心角的度数是 .
11.(2023湖南邵阳中考,16,★☆☆) 如图,某数学兴趣小组用一张半径为30 cm的扇形纸板做成一个圆锥形帽子(接缝忽略不计),如果做成的圆锥形帽子的底面半径为8 cm,那么这张扇形纸板的面积为 cm2.(结果保留π)
12.(2023河北石家庄长安质检,18,★☆☆)如图1,冰激凌的外壳(不计厚度)可近似看做圆锥,其母线长为12 cm,底面圆直径为8 cm.
(1)这个冰激凌外壳的侧面展开图的形状是 ;
(2)当冰激凌被吃掉一部分后,其外壳仍可近似看做圆锥,如图2,其母线长为9 cm,则此时冰激凌外壳的侧面积为 cm2.(结果保留π)
素养探究全练
13.【空间观念】【新考向·阅读理解题】研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.
(1)【阅读材料】
立体图形中既不相交也不平行的两条直线所成的角,就是将一条直线平移使其与另一条直线相交所成的角.
例如,正方体ABCD-A'B'C'D'(图1),因为在平面AA'C'C中,CC'∥AA',AA'与AB相交于点A,所以直线AB与AA'所成的∠BAA'就是既不相交也不平行的两条直线AB与CC'所成的角.
【解决问题】
如图1,已知正方体ABCD-A'B'C'D',求既不相交也不平行的两条直线BA'与AC所成角的大小.
(2)如图2,M,N是正方体相邻两个面上的点.
①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是 .
②在所选正确展开图中,若点M到AB,BC的距离分别是2和5,点N到BD,BC的距离分别是4和3,一只蚂蚁从M点出发,经过线段AB上的某点P,沿正方体表面爬行到N点,则蚂蚁爬行的最短路程是多少
答案全解全析
基础过关全练
1.B 动手操作一下,知拼字所在面与逐字所在面相对,故选B.
2.三棱柱、正方体、圆柱
解析 从题图中三个表面展开图的特征可得由左至右三个几何体依次是三棱柱、正方体、圆柱.
3. 解析 将这个正方体积木的表面展开如图:
连接AC,根据“两点之间线段最短”,可知AC的长就是蜘蛛去抓苍蝇需要爬行的最短路程.
在Rt△ACD中,AC===4(cm).
答:蜘蛛去抓苍蝇需要爬行的最短路程是4 cm.
4.解析 由平面图形的折叠及棱柱的展开图的特征可知,这个几何体是直四棱柱,面A与面F相对,面B与面D相对,面C与面E相对.
(1)如果面D在直棱柱的底部,那么面B会在上面.
(2)如果面A在前面,面D在左面,那么面C会在上面.
(3)如果面C在左面,面D在前面,那么面A会在上面.
5.D 易知该几何体是圆锥,圆锥的侧面展开图如图,连接BD、BC,BD的长即为最短路线长.
设侧面展开图的扇形圆心角为n°,∵扇形弧长=底面圆周长,∴4π=,∴n=120,∴∠BAC=60°,∵AB=AC,∴△ABC是等边三角形,∵D为AC的中点,∴BD⊥AC,AD=AC=3.由勾股定理得BD2=AB2-AD2=27,∴BD=3.故选D.
能力提升全练
6.B 正方体的表面展开图,相对的面之间一定相隔一个正方形,易知“城”字所在面与“明”字所在面相对,故选B.
7.B 由题意可得正方体中面A,面B,面C为相邻面,
由A选项中的展开图可得面A,面C为相对面,故选项A不符合题意;由B选项中的展开图可得面A,面B,面C为相邻面,故选项B符合题意;由C选项中的展开图可得面B,面C为相对面,故选项C不符合题意;由D选项中的展开图可得面A,面B为相对面,故选项D不符合题意.故选B.
8.D D选项中有一对相对面在同一侧,不是长方体的展开图,故此选项符合题意.故选D.
9.B 圆锥的侧面展开图如图所示,AC即为所求,过点B作BD⊥AC于点D,
∵=20π,∴n=120,∴侧面展开图的圆心角为120°.∵∠ABC=120°,BA=BC,∴∠BAC=30°,∴BD=AB=15 cm,
∴AD==15 cm,∴AC=2AD=30 cm,
故彩带的最短长度为30 cm.
方法解读 曲面变平面:利用了转化思想,由几何体通过空间想象得到侧面展开图,构造直角三角形,结合勾股定理求最值.
10.120°
解析 设这种圆锥的侧面展开图的圆心角的度数为n°,则=2×π×10,解得n=120,故答案为120°.
11.240π
解析 帽子底面圆周长为2×8π=16π(cm),即扇形弧长为16π cm,故扇形面积为lr=×16π×30=240π(cm2).故答案为240π.
12.(1)扇形 (2)27π
解析 (1)由圆锥的性质可知其侧面展开图是扇形.
(2)设题图1中圆锥的侧面展开图对应扇形的圆心角的度数为n°,则8π=,解得n=120.
题图2中圆锥的母线长为9 cm,此时冰激凌外壳的侧面积为=27π(cm2).
素养探究全练
13.解析 (1)连接BC',
∵AC∥A'C',BA'与A'C'相交于点A',∴既不相交也不平行的两条直线BA'与AC所成角为∠BA'C',根据正方体性质可得A'B=BC'=A'C',∴△A'BC'为等边三角形,∴∠BA'C'=60°,∴既不相交也不平行的两条直线BA'与AC所成角为60°.
(2)①根据正方体展开图可以判断,题图甲与原图形中对应点位置不符,题图乙不能拼成正方体,故答案为丙.
②如图,作M关于直线AB的对称点M',
连接NM',与AB交于点P,连接MP,则PM+PN=PM'+PN=NM',此时爬行的路程最短.过点N作BC垂线,并延长与直线M'M交于点E,
∵点M到BC的距离是5,点N到BC的距离是3,
∴NE=8,∵点M到AB的距离是2,点N到BD的距离是4,∴EM'=6,∴NM'===10,故蚂蚁爬行的最短路程为10.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
