2024冀教版数学九年级下学期课时练--专项素养综合全练(二)与三角形内切圆有关的计算与证明(含解析)
文档属性
| 名称 | 2024冀教版数学九年级下学期课时练--专项素养综合全练(二)与三角形内切圆有关的计算与证明(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 366.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 17:50:58 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
专项素养综合全练(二)
与三角形内切圆有关的计算与证明
类型一 应用切线长定理
如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,☉O是它的内切圆,小明准备用剪刀在☉O的右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则剪下的三角形AMN的周长为( )
A.12 cm
B.7 cm
C.6 cm
D.随直线MN的变化而变化
2.如图,在Rt△ABC中,∠C=90°,AC=5,☉O是△ABC的内切圆,半径为2,则图中阴影部分的面积为 ( )
A.30-4π B.30-4π
C.60-16π D.30-16π
类型二 常用辅助线的作法
3.如图,△ABC中,内切圆I和边BC、AC、AB分别相切于点D、E、F,若∠B=55°,∠C=75°,则∠EDF的度数是 ( )
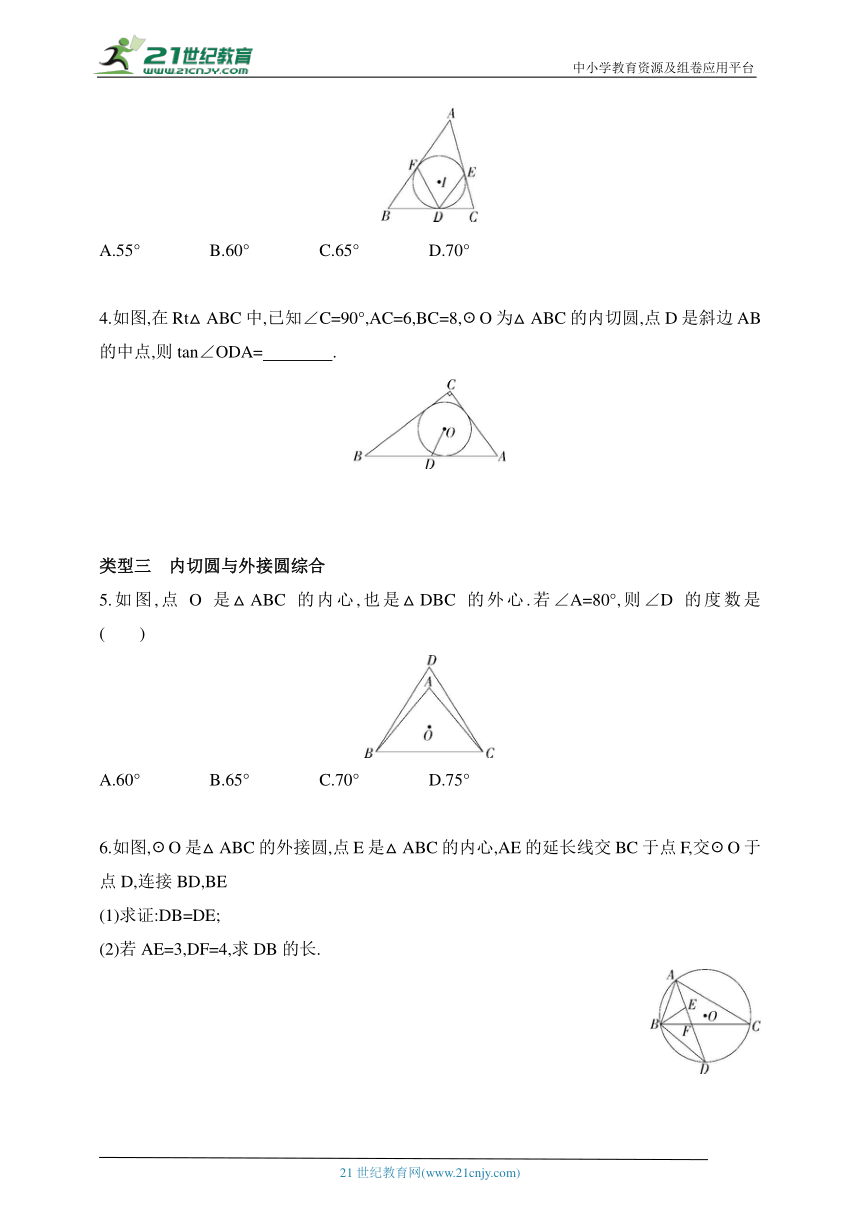
A.55° B.60° C.65° D.70°
4.如图,在Rt△ABC中,已知∠C=90°,AC=6,BC=8,☉O为△ABC的内切圆,点D是斜边AB的中点,则tan∠ODA= .
类型三 内切圆与外接圆综合
5.如图,点O是△ABC的内心,也是△DBC的外心.若∠A=80°,则∠D的度数是 ( )
A.60° B.65° C.70° D.75°
6.如图,☉O是△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交☉O于点D,连接BD,BE
(1)求证:DB=DE;
(2)若AE=3,DF=4,求DB的长.
答案全解全析
1.B 如图,设E、F、G分别是☉O与△ABC各边的切点,∴DM=MF,
EN=FN,BD=BG,CG=CE,∴BD+CE=BG+CG=BC.
∵AB+BC+AC=17 cm,BD+CE+BC=2BC=10 cm,∴AD+AE=7 cm,∴AM+AN+MN=AM+AN+MF+NF=AM+AN+DM+EN=AD+AE=7 cm.故选B.
2.A 如图,记三个切点分别为D、E、F,连接OD、OE、OF,
则∠ODC=∠OEC=∠OFA=90°,OD=OE=OF=2,
又∠C=90°,∴四边形ODCE是正方形,
∴CE=CD=2,∵☉O是△ABC的内切圆,∴AE=AF=5-2=3,BD=BF,设BD=BF=x,则BC=x+2,AB=x+3,在Rt△ABC中,52+(x+2)2=(x+3)2,
∴x=10,∴BC=12,∴S阴影=S△ABC-S☉O=×5×12-π×22=30-4π.故选A.
3.C 连接IE、IF,∵内切圆I和边AC、AB分别相切于点E、F,∴IE⊥AC,IF⊥AB,∴∠AEI=∠AFI=90°,∴∠EIF=180°-∠A,∵∠EDF=∠EIF,∴∠EDF=90°-∠A,∵∠B=55°,∠C=75°,∴∠A=180°-∠B-∠C=50°,∴∠EDF=90°-×50°=65°.故选C.
4.2
解析 如图,设圆O与AC切于点F,与BC切于点H,与AB切于点E,连接OF、OH、OE,
则OF⊥AC,OH⊥BC,OE⊥AB,OF=OH=OE,
∵∠C=90°,∴四边形CHOF为正方形,设其边长为r,∵AC=6,BC=8,∴AB==10,∵D是AB的中点,∴AD=5,
∵S△ACB=BC·AC=(AB+BC+CA)r,
∴r==2,∴AE=AF=AC-CF=4,∴DE=AD-AE=1,∴tan∠ODA===2.故答案为2.
5.B 连接OB,OC,
∵点O是△ABC的内心,
∴BO,CO分别是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠BOC=180°-∠OBC-∠OCB=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A=130°,
∵点O是△DBC的外心,∴∠D=∠BOC=65°.
6.解析 (1)证明:∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAD=∠CAD,∠ABE=∠CBE,
又∵∠CAD与∠CBD所对的弧均为,
∴∠BAD=∠CAD=∠CBD,∵∠BED=∠ABE+∠BAD,∠DBE=∠CBE+∠CBD,∴∠BED=∠DBE,∴DB=DE.
(2)∵∠D=∠D,∠DBF=∠CAD=∠BAD,
∴△ABD∽△BFD,∴=①,
设EF=x,∵DF=4,AE=3,∴DB=DE=4+x,AD=7+x,
代入①式得=,解得x1=2,x2=-6(不合题意,舍去),则DB=4+x=4+2=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
专项素养综合全练(二)
与三角形内切圆有关的计算与证明
类型一 应用切线长定理
如图,△ABC是一张周长为17 cm的三角形纸片,BC=5 cm,☉O是它的内切圆,小明准备用剪刀在☉O的右侧沿着与☉O相切的任意一条直线MN剪下△AMN,则剪下的三角形AMN的周长为( )
A.12 cm
B.7 cm
C.6 cm
D.随直线MN的变化而变化
2.如图,在Rt△ABC中,∠C=90°,AC=5,☉O是△ABC的内切圆,半径为2,则图中阴影部分的面积为 ( )
A.30-4π B.30-4π
C.60-16π D.30-16π
类型二 常用辅助线的作法
3.如图,△ABC中,内切圆I和边BC、AC、AB分别相切于点D、E、F,若∠B=55°,∠C=75°,则∠EDF的度数是 ( )
A.55° B.60° C.65° D.70°
4.如图,在Rt△ABC中,已知∠C=90°,AC=6,BC=8,☉O为△ABC的内切圆,点D是斜边AB的中点,则tan∠ODA= .
类型三 内切圆与外接圆综合
5.如图,点O是△ABC的内心,也是△DBC的外心.若∠A=80°,则∠D的度数是 ( )
A.60° B.65° C.70° D.75°
6.如图,☉O是△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交☉O于点D,连接BD,BE
(1)求证:DB=DE;
(2)若AE=3,DF=4,求DB的长.
答案全解全析
1.B 如图,设E、F、G分别是☉O与△ABC各边的切点,∴DM=MF,
EN=FN,BD=BG,CG=CE,∴BD+CE=BG+CG=BC.
∵AB+BC+AC=17 cm,BD+CE+BC=2BC=10 cm,∴AD+AE=7 cm,∴AM+AN+MN=AM+AN+MF+NF=AM+AN+DM+EN=AD+AE=7 cm.故选B.
2.A 如图,记三个切点分别为D、E、F,连接OD、OE、OF,
则∠ODC=∠OEC=∠OFA=90°,OD=OE=OF=2,
又∠C=90°,∴四边形ODCE是正方形,
∴CE=CD=2,∵☉O是△ABC的内切圆,∴AE=AF=5-2=3,BD=BF,设BD=BF=x,则BC=x+2,AB=x+3,在Rt△ABC中,52+(x+2)2=(x+3)2,
∴x=10,∴BC=12,∴S阴影=S△ABC-S☉O=×5×12-π×22=30-4π.故选A.
3.C 连接IE、IF,∵内切圆I和边AC、AB分别相切于点E、F,∴IE⊥AC,IF⊥AB,∴∠AEI=∠AFI=90°,∴∠EIF=180°-∠A,∵∠EDF=∠EIF,∴∠EDF=90°-∠A,∵∠B=55°,∠C=75°,∴∠A=180°-∠B-∠C=50°,∴∠EDF=90°-×50°=65°.故选C.
4.2
解析 如图,设圆O与AC切于点F,与BC切于点H,与AB切于点E,连接OF、OH、OE,
则OF⊥AC,OH⊥BC,OE⊥AB,OF=OH=OE,
∵∠C=90°,∴四边形CHOF为正方形,设其边长为r,∵AC=6,BC=8,∴AB==10,∵D是AB的中点,∴AD=5,
∵S△ACB=BC·AC=(AB+BC+CA)r,
∴r==2,∴AE=AF=AC-CF=4,∴DE=AD-AE=1,∴tan∠ODA===2.故答案为2.
5.B 连接OB,OC,
∵点O是△ABC的内心,
∴BO,CO分别是∠ABC,∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠BOC=180°-∠OBC-∠OCB=180°-(∠ABC+∠ACB)=180°-(180°-∠A)=90°+∠A=130°,
∵点O是△DBC的外心,∴∠D=∠BOC=65°.
6.解析 (1)证明:∵点E是△ABC的内心,
∴AE平分∠BAC,BE平分∠ABC,
∴∠BAD=∠CAD,∠ABE=∠CBE,
又∵∠CAD与∠CBD所对的弧均为,
∴∠BAD=∠CAD=∠CBD,∵∠BED=∠ABE+∠BAD,∠DBE=∠CBE+∠CBD,∴∠BED=∠DBE,∴DB=DE.
(2)∵∠D=∠D,∠DBF=∠CAD=∠BAD,
∴△ABD∽△BFD,∴=①,
设EF=x,∵DF=4,AE=3,∴DB=DE=4+x,AD=7+x,
代入①式得=,解得x1=2,x2=-6(不合题意,舍去),则DB=4+x=4+2=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
