2024冀教版数学九年级下学期课时练--专项素养综合全练(三)二次函数图像与系数a、b、c的关系(含解析)
文档属性
| 名称 | 2024冀教版数学九年级下学期课时练--专项素养综合全练(三)二次函数图像与系数a、b、c的关系(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 364.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 17:53:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
专项素养综合全练(三)
二次函数图像与系数a、b、c的关系
类型一 判断a、b、c的符号
1.如果a<0,b>0,c<0,那么二次函数y=ax2+bx+c的图像可能是 ( )
A B C D
2.二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列说法不正确的是( )
A.函数有最小值 B.a>0
C.c>0 D.-<0
类型二 判断a、b、c的等量关系
已知二次函数y=ax2+bx+c(a≠0)的部分图像如图所示,有下列结论:①abc<0;②当x=-1时,y=0;③a+2b=c;④y最大值=c.其中正确的有
( )
A.1个 B.2个 C.3个 D.4个
类型三 判断含a、b、c的代数式与0的不等关系
4.二次函数y=ax2+bx+c(a≠0)的图像如图所示,下列选项错误的是( )
A.ac<0
B.x>1时,y随x的增大而增大
C.a+b+c>0
D.图像与直线y=2有两个交点
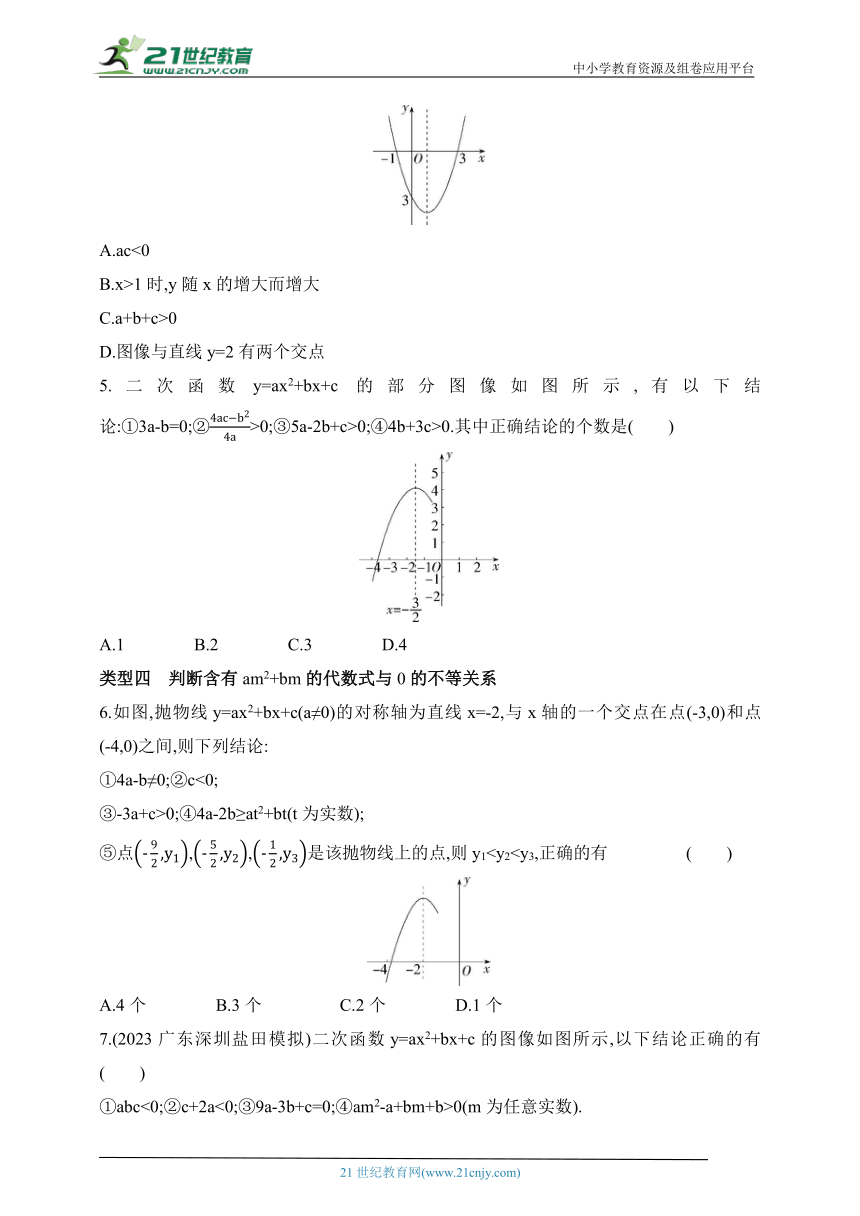
5.二次函数y=ax2+bx+c的部分图像如图所示,有以下结论:①3a-b=0;②>0;③5a-2b+c>0;④4b+3c>0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
类型四 判断含有am2+bm的代数式与0的不等关系
6.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在点(-3,0)和点(-4,0)之间,则下列结论:
①4a-b≠0;②c<0;
③-3a+c>0;④4a-2b≥at2+bt(t为实数);
⑤点,,是该抛物线上的点,则y1A.4个 B.3个 C.2个 D.1个
7.(2023广东深圳盐田模拟)二次函数y=ax2+bx+c的图像如图所示,以下结论正确的有 ( )
①abc<0;②c+2a<0;③9a-3b+c=0;④am2-a+bm+b>0(m为任意实数).
A.1个 B.2个 C.3个 D.4个
答案全解全析
1.A ∵a<0,∴函数图像开口向下,∵a,b异号,∴对称轴在y轴右侧,∵c<0,∴抛物线与y轴交于负半轴上一点,故选A.
2.D 因为函数图像开口向上,所以a>0,函数有最小值,故A,B选项说法正确.因为抛物线与y轴交于正半轴,所以c>0,故C选项说法正确.因为对称轴在y轴右侧,所以->0,故D选项说法错误.
3.D ∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=-=1,∴b=-2a>0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,∴①正确;
∵点(3,0)在函数图像上,图像对称轴为直线x=1,∴点(-1,0)也在函数图像上,∴x=-1时,y=0,∴②正确;
∵当x=-1时,y=0,∴a-b+c=0,又∵b=-2a,∴a+2a+c=0,即c=-3a,∴a+2b-c=a-4a+3a=0,即a+2b=c,∴③正确;
由图像可知当x=1时,函数y取得最大值,为a+b+c=a-2a+c=-a+c=c+c=c,∴④正确.故选D.
4.C A.由二次函数的图像开口向上可得a>0,由抛物线与y轴交于负半轴可得c<0,所以ac<0;
B.由a>0,对称轴为直线x==1,可知x>1时,y随x的增大而增大;
C.由函数图像可以看出x=1时二次函数的值为负,∴x=1时,y=a+b+c<0;
D.由二次函数的图像可知图像与直线y=2有两个交点.故选C.
5.C 由图像可知a<0,c>0,对称轴为直线x=-,
∴-=-,∴b=3a,∴3a-b=0,①正确;
∵函数图像的顶点在第二象限,且a<0,∴函数的最大值大于0,故>0,②正确;
当x=-1时,y=a-b+c>0,
当x=-3时,y=9a-3b+c>0,
∴10a-4b+2c>0,∴5a-2b+c>0,③正确;
由对称性可知x=1时对应的y值与x=-4时对应的y值相等,∴当x=1时,y=a+b+c<0,
∵b=3a,∴4b+3c=3b+b+3c=3b+3a+3c=3(a+b+c)<0,∴4b+3c<0,④错误.
①②③结论正确,故选C.
6.B ①抛物线的对称轴为直线x=-=-2,所以4a-b=0,所以①错误;
②抛物线y=ax2+bx+c与x轴的一个交点在点(-3,0)和点(-4,0)之间,由抛物线的对称性可知抛物线与x轴的另一个交点在点(-1,0)和点(0,0)之间,所以抛物线与y轴的交点在y轴的负半轴上,即c<0,故②正确;
③由①可知4a-b=0,由图像知x=-3时,y>0,即y=9a-3b+c>0,所以将Ⅰ代入Ⅱ并消掉b可得-3a+c>0,故③正确;
④由函数图像知当x=-2时,函数取得最大值,所以4a-2b+c≥at2+bt+c(t为实数),即4a-2b≥at2+bt(t为实数),故④正确;
⑤点-,y1,-,y2,-,y3是该抛物线上的点,这三个点到对称轴的距离分别为d1=,d2=,d3=,抛物线开口向下,离对称轴越近,函数值越大,故由d1>d3>d2,可知y1综上可知,正确的有3个.故选B.
7.C ∵抛物线开口向上,∴a>0,由对称轴可知-=-1<0,∴a、b同号,∴b>0,∵抛物线与y轴的交点在y轴的负半轴上,∴c<0,∴abc<0,因此①正确;
∵抛物线过点(1,0),∴a+b+c=0,又∵对称轴为直线x=-1,∴-=-1,∴b=2a,∴a+2a+c=0,即3a+c=0,而a>0,∴2a+c<3a+c=0,因此②正确;
由图像可知,抛物线与x轴的一个交点坐标为(1,0),而对称轴为直线x=-1,由对称性可知,抛物线与x轴的另一个交点坐标为(-3,0),∴9a-3b+c=0,因此③正确;
由二次函数的图像可知,当x=-1时,y取得最小值,y最小值=a-b+c,当x=m时,y=am2+bm+c,有am2+bm+c≥a-b+c,即am2+bm-a+b≥0,因此④不正确.
正确的结论有①②③,共3个,故选C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
专项素养综合全练(三)
二次函数图像与系数a、b、c的关系
类型一 判断a、b、c的符号
1.如果a<0,b>0,c<0,那么二次函数y=ax2+bx+c的图像可能是 ( )
A B C D
2.二次函数y=ax2+bx+c(a≠0)的图像如图所示,则下列说法不正确的是( )
A.函数有最小值 B.a>0
C.c>0 D.-<0
类型二 判断a、b、c的等量关系
已知二次函数y=ax2+bx+c(a≠0)的部分图像如图所示,有下列结论:①abc<0;②当x=-1时,y=0;③a+2b=c;④y最大值=c.其中正确的有
( )
A.1个 B.2个 C.3个 D.4个
类型三 判断含a、b、c的代数式与0的不等关系
4.二次函数y=ax2+bx+c(a≠0)的图像如图所示,下列选项错误的是( )
A.ac<0
B.x>1时,y随x的增大而增大
C.a+b+c>0
D.图像与直线y=2有两个交点
5.二次函数y=ax2+bx+c的部分图像如图所示,有以下结论:①3a-b=0;②>0;③5a-2b+c>0;④4b+3c>0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
类型四 判断含有am2+bm的代数式与0的不等关系
6.如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在点(-3,0)和点(-4,0)之间,则下列结论:
①4a-b≠0;②c<0;
③-3a+c>0;④4a-2b≥at2+bt(t为实数);
⑤点,,是该抛物线上的点,则y1
7.(2023广东深圳盐田模拟)二次函数y=ax2+bx+c的图像如图所示,以下结论正确的有 ( )
①abc<0;②c+2a<0;③9a-3b+c=0;④am2-a+bm+b>0(m为任意实数).
A.1个 B.2个 C.3个 D.4个
答案全解全析
1.A ∵a<0,∴函数图像开口向下,∵a,b异号,∴对称轴在y轴右侧,∵c<0,∴抛物线与y轴交于负半轴上一点,故选A.
2.D 因为函数图像开口向上,所以a>0,函数有最小值,故A,B选项说法正确.因为抛物线与y轴交于正半轴,所以c>0,故C选项说法正确.因为对称轴在y轴右侧,所以->0,故D选项说法错误.
3.D ∵抛物线开口向下,∴a<0,∵抛物线的对称轴为直线x=-=1,∴b=-2a>0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,∴①正确;
∵点(3,0)在函数图像上,图像对称轴为直线x=1,∴点(-1,0)也在函数图像上,∴x=-1时,y=0,∴②正确;
∵当x=-1时,y=0,∴a-b+c=0,又∵b=-2a,∴a+2a+c=0,即c=-3a,∴a+2b-c=a-4a+3a=0,即a+2b=c,∴③正确;
由图像可知当x=1时,函数y取得最大值,为a+b+c=a-2a+c=-a+c=c+c=c,∴④正确.故选D.
4.C A.由二次函数的图像开口向上可得a>0,由抛物线与y轴交于负半轴可得c<0,所以ac<0;
B.由a>0,对称轴为直线x==1,可知x>1时,y随x的增大而增大;
C.由函数图像可以看出x=1时二次函数的值为负,∴x=1时,y=a+b+c<0;
D.由二次函数的图像可知图像与直线y=2有两个交点.故选C.
5.C 由图像可知a<0,c>0,对称轴为直线x=-,
∴-=-,∴b=3a,∴3a-b=0,①正确;
∵函数图像的顶点在第二象限,且a<0,∴函数的最大值大于0,故>0,②正确;
当x=-1时,y=a-b+c>0,
当x=-3时,y=9a-3b+c>0,
∴10a-4b+2c>0,∴5a-2b+c>0,③正确;
由对称性可知x=1时对应的y值与x=-4时对应的y值相等,∴当x=1时,y=a+b+c<0,
∵b=3a,∴4b+3c=3b+b+3c=3b+3a+3c=3(a+b+c)<0,∴4b+3c<0,④错误.
①②③结论正确,故选C.
6.B ①抛物线的对称轴为直线x=-=-2,所以4a-b=0,所以①错误;
②抛物线y=ax2+bx+c与x轴的一个交点在点(-3,0)和点(-4,0)之间,由抛物线的对称性可知抛物线与x轴的另一个交点在点(-1,0)和点(0,0)之间,所以抛物线与y轴的交点在y轴的负半轴上,即c<0,故②正确;
③由①可知4a-b=0,由图像知x=-3时,y>0,即y=9a-3b+c>0,所以将Ⅰ代入Ⅱ并消掉b可得-3a+c>0,故③正确;
④由函数图像知当x=-2时,函数取得最大值,所以4a-2b+c≥at2+bt+c(t为实数),即4a-2b≥at2+bt(t为实数),故④正确;
⑤点-,y1,-,y2,-,y3是该抛物线上的点,这三个点到对称轴的距离分别为d1=,d2=,d3=,抛物线开口向下,离对称轴越近,函数值越大,故由d1>d3>d2,可知y1
7.C ∵抛物线开口向上,∴a>0,由对称轴可知-=-1<0,∴a、b同号,∴b>0,∵抛物线与y轴的交点在y轴的负半轴上,∴c<0,∴abc<0,因此①正确;
∵抛物线过点(1,0),∴a+b+c=0,又∵对称轴为直线x=-1,∴-=-1,∴b=2a,∴a+2a+c=0,即3a+c=0,而a>0,∴2a+c<3a+c=0,因此②正确;
由图像可知,抛物线与x轴的一个交点坐标为(1,0),而对称轴为直线x=-1,由对称性可知,抛物线与x轴的另一个交点坐标为(-3,0),∴9a-3b+c=0,因此③正确;
由二次函数的图像可知,当x=-1时,y取得最小值,y最小值=a-b+c,当x=m时,y=am2+bm+c,有am2+bm+c≥a-b+c,即am2+bm-a+b≥0,因此④不正确.
正确的结论有①②③,共3个,故选C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
