2024冀教版数学九年级下学期课时练--专项素养综合全练(四)二次函数与几何图形的综合应用(含解析)
文档属性
| 名称 | 2024冀教版数学九年级下学期课时练--专项素养综合全练(四)二次函数与几何图形的综合应用(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 17:53:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
专项素养综合全练(四)
二次函数与几何图形的综合应用
类型一 线段最值问题
1.【函数思想】(2023山东菏泽中考)已知抛物线y=-x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,4),其对称轴为直线x=-.
(1)求抛物线的表达式;
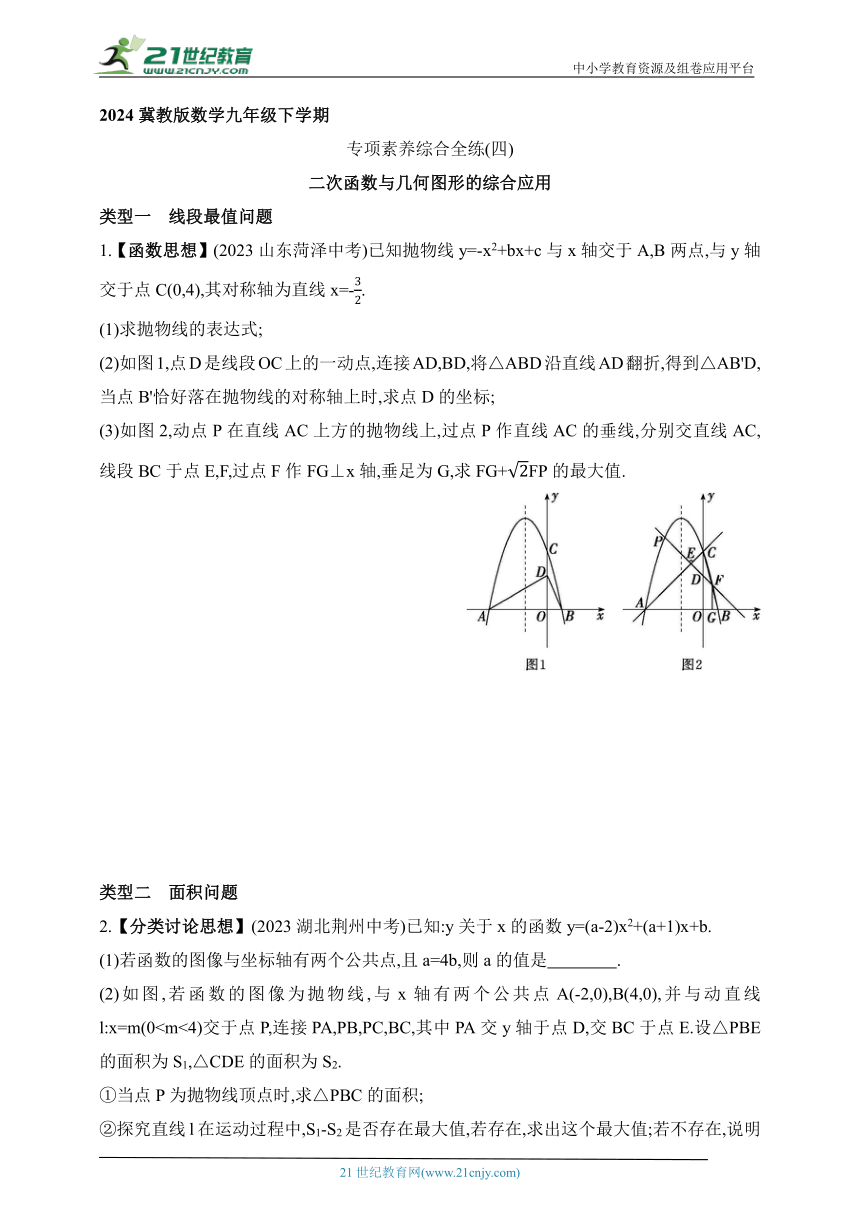
(2)如图1,点D是线段OC上的一动点,连接AD,BD,将△ABD沿直线AD翻折,得到△AB'D,当点B'恰好落在抛物线的对称轴上时,求点D的坐标;
(3)如图2,动点P在直线AC上方的抛物线上,过点P作直线AC的垂线,分别交直线AC,线段BC于点E,F,过点F作FG⊥x轴,垂足为G,求FG+FP的最大值.
类型二 面积问题
2.【分类讨论思想】(2023湖北荆州中考)已知:y关于x的函数y=(a-2)x2+(a+1)x+b.
(1)若函数的图像与坐标轴有两个公共点,且a=4b,则a的值是 .
(2)如图,若函数的图像为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:x=m(0①当点P为抛物线顶点时,求△PBC的面积;
②探究直线l在运动过程中,S1-S2是否存在最大值,若存在,求出这个最大值;若不存在,说明理由.
类型三 与平行四边形有关的问题
3. (2023山东聊城中考)如图1,抛物线y=ax2+bx-9与x轴交于点A(-3,0),B(6,0),与y轴交于点C,连接AC,BC.点P是x轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,当以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;
(3)如图2,当点P(m,0)从点A出发沿x轴向点B运动时(点P与点A,B不重合),过点P分别作PE∥BC,交AC于点E,作PD⊥BC,垂足为点D,当m为何值时,△PED的面积最大 并求出最大值.
类型四 角度存在性问题
4. 【等角转化法】(2023湖南郴州中考)已知抛物线y=ax2+bx+4与x轴相交于点A(1,0),B(4,0),与y轴相交于点C.
(1)求抛物线的表达式;
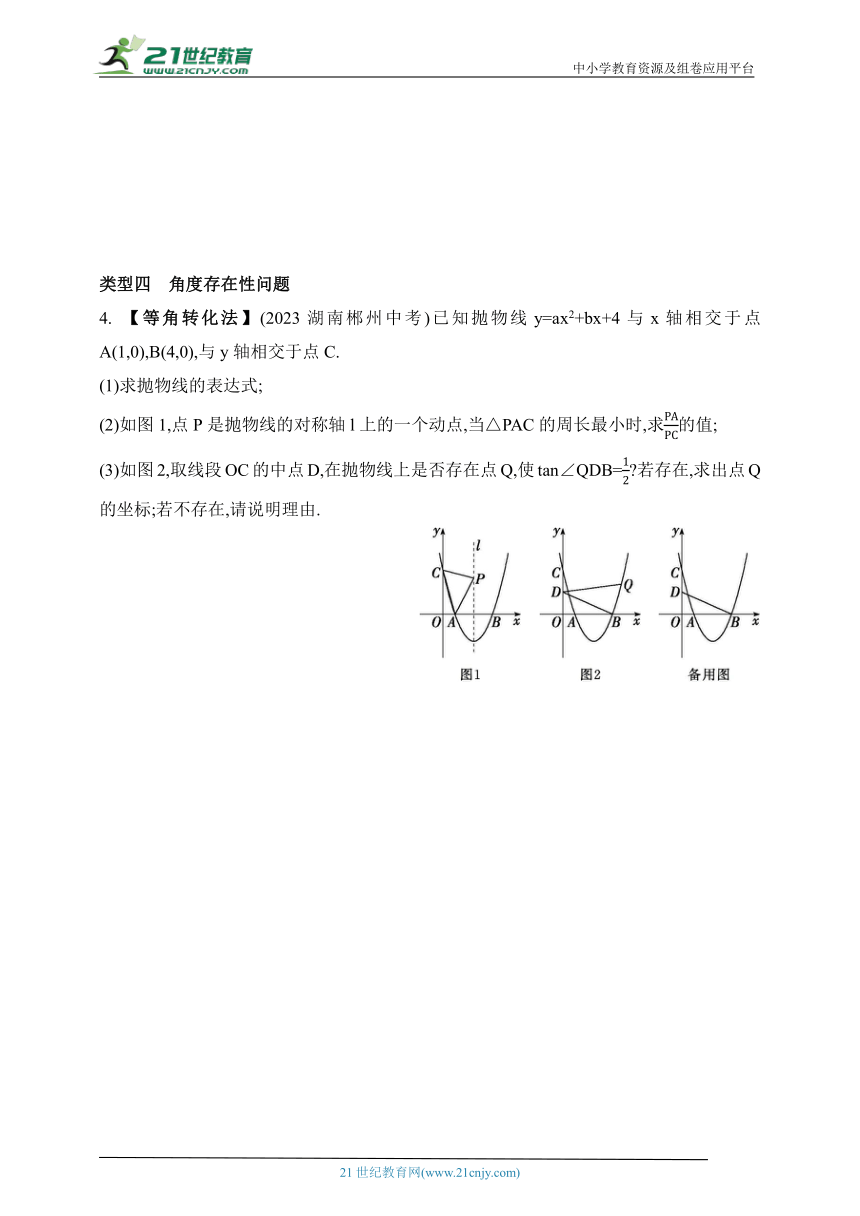
(2)如图1,点P是抛物线的对称轴l上的一个动点,当△PAC的周长最小时,求的值;
(3)如图2,取线段OC的中点D,在抛物线上是否存在点Q,使tan∠QDB= 若存在,求出点Q的坐标;若不存在,请说明理由.
答案全解全析
1.解析 (1)∵抛物线与y轴交于点C(0,4),∴c=4,
∵对称轴为直线x=-,∴-=-,∴b=-3,
∴抛物线的解析式为y=-x2-3x+4.
(2)如图,过B'作x轴的垂线,垂足为H,
令-x2-3x+4=0,解得x1=1,x2=-4,
∴A(-4,0),B(1,0),
∴AB=1-(-4)=5,由翻折可得AB'=AB=5,
∵对称轴为直线x=-,
∴AH=--(-4)=,∵AB'=AB=5=2AH,
∴∠AB'H=30°,∴∠B'AB=90°-∠AB'H=60°,
由翻折可知∠B'AD=∠BAD,
∴∠DAB=∠B'AB=30°,
在Rt△AOD中,OD=OA·tan 30°=,
∴D.
(3)设BC所在直线的解析式为y1=k1x+b1(k1≠0),
把B,C点坐标代入,得解得
∴y1=-4x+4,∵OA=OC=4,
∴∠CAO=45°,又∵∠AEF=90°,∴直线PE与x轴所成夹角为45°,
设P(m,-m2-3m+4),
设PE所在直线的解析式为y2=-x+b2,
把点P坐标代入,得-m+b2=-m2-3m+4,
解得b2=-m2-2m+4,∴y2=-x-m2-2m+4,
令y1=y2,则-4x+4=-x-m2-2m+4,解得x=,即F点横坐标为,∴FG=yF=+4,PF==··(xF-xP)=(m2-m),
∴FG+FP=+4+
=-+,
∵点P在直线AC上方,∴-4∴当m=-时,FG+FP取得最大值,为.
2.解析 (1)当函数为一次函数时,a-2=0,
∴a=2,∴y=(2+1)x+=3x+,其图像与x轴,y轴分别有一个交点.
当函数为二次函数时,函数图像与y轴必有一个交点,分情况讨论:(i)当与y轴交点不是原点时,其函数图像与x轴只有一个公共点,
∴令(a-2)x2+(a+1)x+b=0,
∵a=4b,∴(a-2)x2+(a+1)x+=0,
∴Δ=(a+1)2-4(a-2)×=4a+1=0,
∴a=-,∴y=-x2+x-,易得其图像与坐标轴的交点坐标为和,符合题意.
(ii)当与y轴的交点是原点时,易得b=0,∵a=4b,∴a=0,∴y=-2x2+x,易得其图像与坐标轴的交点坐标为(0,0)和,符合题意.
故答案为0或2或-.
(2)如图所示,设直线l与BC交于点F,直线l与x轴交于点H.
将A,B点坐标代入解析式,
得
解得
∴抛物线的解析式为y=-x2+2x+8=-(x-1)2+9,
∴C(0,8).
①当点P为抛物线顶点时,P(1,9),
∴PH=9,xP=1,
由B(4,0),C(0,8)易得直线BC的解析式为y=-2x+8,
∵F在直线l上,∴F的横坐标等于P的横坐标,
∴xF=1,∵F在直线BC:y=-2x+8上,
∴F(1,6),∴FH=6,OH=1,
∴PF=PH-FH=9-6=3,BH=OB-OH=4-1=3,
∴S△PBC=S△PFC+S△PFB=xP·PF+HB·PF
=×1×3+×3×3=6,即△PBC的面积为6.
②S1-S2存在最大值.
易知OB=4,AO=2,AB=6,OC=8,AH=2+m,P(m,-m2+2m+8),
∴PH=-m2+2m+8,∵OD⊥x轴,PH⊥x轴,
∴OD∥PH,∴=,即=,
∴OD=8-2m.
∵S1=S△PBE=S△PAB-S△AOD-S四边形EDOB,S2=S△CDE=S△OBC-S四边形EDOB,
∴S1-S2=S△PAB-S△AOD-S△OBC=--=--=-3m2+8m=-3+,∵-3<0,0∴当m=时,S1-S2取得最大值,最大值为.
3.解析 (1)将A(-3,0),B(6,0)的坐标代入y=ax2+bx-9,得解得
∴抛物线的表达式为y=x2-x-9.
(2)易知点C(0,-9),
设点P(m,0),点Q,在A,C,P,Q四点组成的平行四边形中,当AC为边,AQ为对角线时(如图1),
∵四边形ACQP为平行四边形,∴AP∥CQ,∴yQ=yC,∴n2-n-9=-9,解得n=0(舍去)或n=3,
∴点Q(3,-9).
在A,C,P,Q四点组成的平行四边形中,当AC为边,AP为对角线时(如图2),连接CQ,
线段CQ的中点在x轴上,∴yC+yQ=0,∴n2-n-9+(-9)=0,解得n=+或n=-,
∵yQ=-yC=9,
∴点Q的坐标为或.
综上,点Q的坐标为(3,-9)或或.
(3)设△PED的面积为S,
由题意得AP=m+3,BP=6-m,OB=6,OC=9,AB=9,∴BC==3,
∵sin∠PBD==,∴=,
∴PD=,
∵PE∥BC,∴△APE∽△ABC,∠EPD=∠PDB=90°,
∴=,∴=,∴PE=,
∴S=PE·PD=(m+3)(6-m)=-+,∴当m=时,S取得最大值,为,
∴当m=时,△PED的面积最大,为.
4.解析 (1)∵抛物线y=ax2+bx+4与x轴相交于点A(1,0),B(4,0),
∴解得
∴抛物线的表达式为y=x2-5x+4.
(2)易知C(0,4),抛物线的对称轴为直线x=.
∵△PAC的周长=PA+PC+AC,AC为定长,∴当PA+PC的值最小时,△PAC的周长最小,
∵点A,B关于对称轴对称,
∴PA+PC=PB+PC≥BC,故当P,B,C三点共线时,PA+PC的值最小,为BC的长,此时点P为直线BC与对称轴的交点,
由B(4,0),C(0,4)易得直线BC的解析式为y=-x+4,当x=时,y=-+4=,
∴P,∵A(1,0),C(0,4),
∴PA==,
PC==,∴=.
(3)存在.
∵D为OC的中点,∴D(0,2),∴OD=2,
∵B(4,0),∴OB=4,
在Rt△BOD中,tan∠OBD==,
∵tan∠QDB==tan∠OBD,∴∠QDB=∠OBD.
分情况讨论:①当Q点与D点在平行于x轴的直线上时,过点D作平行于x轴的直线,交抛物线于点Q1和Q2,如图,则∠Q1DB=∠OBD,此时点Q1,Q2的纵坐标为2,
设点Q1的横坐标为t1,点Q2的横坐标为t2,则t1,t2满足t2-5t+4=2,解得t1=,t2=,
∴Q1,Q2.
②当Q点在D点所在水平线的下方,即yQ则DE=BE,设E(p,0),则DE2=OE2+OD2=p2+4,BE2=(4-p)2,∴p2+4=(4-p)2,
解得p=,∴E,
设直线DE的解析式为y=kx+q(k≠0),
代入D,E两点的坐标,
得解得∴y=-x+2,
联立抛物线与直线DE,得解得或∴Q3,Q4(3,-2).
综上,点Q的坐标为或或(3,-2)或.
方法解读 等角转化法:构造全等三角形、相似三角形,在这两类三角形中,对应角相等;由平行线的性质可知两直线平行,同位角相等,内错角相等;在同圆或等圆中,同弧或等弧所对的圆周角、圆心角相等;当两个锐角的三角函数值相等时,两锐角相等.我们常借助以上知识达到等角转化的目的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
专项素养综合全练(四)
二次函数与几何图形的综合应用
类型一 线段最值问题
1.【函数思想】(2023山东菏泽中考)已知抛物线y=-x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,4),其对称轴为直线x=-.
(1)求抛物线的表达式;
(2)如图1,点D是线段OC上的一动点,连接AD,BD,将△ABD沿直线AD翻折,得到△AB'D,当点B'恰好落在抛物线的对称轴上时,求点D的坐标;
(3)如图2,动点P在直线AC上方的抛物线上,过点P作直线AC的垂线,分别交直线AC,线段BC于点E,F,过点F作FG⊥x轴,垂足为G,求FG+FP的最大值.
类型二 面积问题
2.【分类讨论思想】(2023湖北荆州中考)已知:y关于x的函数y=(a-2)x2+(a+1)x+b.
(1)若函数的图像与坐标轴有两个公共点,且a=4b,则a的值是 .
(2)如图,若函数的图像为抛物线,与x轴有两个公共点A(-2,0),B(4,0),并与动直线l:x=m(0
②探究直线l在运动过程中,S1-S2是否存在最大值,若存在,求出这个最大值;若不存在,说明理由.
类型三 与平行四边形有关的问题
3. (2023山东聊城中考)如图1,抛物线y=ax2+bx-9与x轴交于点A(-3,0),B(6,0),与y轴交于点C,连接AC,BC.点P是x轴上任意一点.
(1)求抛物线的表达式;
(2)点Q在抛物线上,当以点A,C,P,Q为顶点,AC为一边的四边形为平行四边形时,求点Q的坐标;
(3)如图2,当点P(m,0)从点A出发沿x轴向点B运动时(点P与点A,B不重合),过点P分别作PE∥BC,交AC于点E,作PD⊥BC,垂足为点D,当m为何值时,△PED的面积最大 并求出最大值.
类型四 角度存在性问题
4. 【等角转化法】(2023湖南郴州中考)已知抛物线y=ax2+bx+4与x轴相交于点A(1,0),B(4,0),与y轴相交于点C.
(1)求抛物线的表达式;
(2)如图1,点P是抛物线的对称轴l上的一个动点,当△PAC的周长最小时,求的值;
(3)如图2,取线段OC的中点D,在抛物线上是否存在点Q,使tan∠QDB= 若存在,求出点Q的坐标;若不存在,请说明理由.
答案全解全析
1.解析 (1)∵抛物线与y轴交于点C(0,4),∴c=4,
∵对称轴为直线x=-,∴-=-,∴b=-3,
∴抛物线的解析式为y=-x2-3x+4.
(2)如图,过B'作x轴的垂线,垂足为H,
令-x2-3x+4=0,解得x1=1,x2=-4,
∴A(-4,0),B(1,0),
∴AB=1-(-4)=5,由翻折可得AB'=AB=5,
∵对称轴为直线x=-,
∴AH=--(-4)=,∵AB'=AB=5=2AH,
∴∠AB'H=30°,∴∠B'AB=90°-∠AB'H=60°,
由翻折可知∠B'AD=∠BAD,
∴∠DAB=∠B'AB=30°,
在Rt△AOD中,OD=OA·tan 30°=,
∴D.
(3)设BC所在直线的解析式为y1=k1x+b1(k1≠0),
把B,C点坐标代入,得解得
∴y1=-4x+4,∵OA=OC=4,
∴∠CAO=45°,又∵∠AEF=90°,∴直线PE与x轴所成夹角为45°,
设P(m,-m2-3m+4),
设PE所在直线的解析式为y2=-x+b2,
把点P坐标代入,得-m+b2=-m2-3m+4,
解得b2=-m2-2m+4,∴y2=-x-m2-2m+4,
令y1=y2,则-4x+4=-x-m2-2m+4,解得x=,即F点横坐标为,∴FG=yF=+4,PF==··(xF-xP)=(m2-m),
∴FG+FP=+4+
=-+,
∵点P在直线AC上方,∴-4
2.解析 (1)当函数为一次函数时,a-2=0,
∴a=2,∴y=(2+1)x+=3x+,其图像与x轴,y轴分别有一个交点.
当函数为二次函数时,函数图像与y轴必有一个交点,分情况讨论:(i)当与y轴交点不是原点时,其函数图像与x轴只有一个公共点,
∴令(a-2)x2+(a+1)x+b=0,
∵a=4b,∴(a-2)x2+(a+1)x+=0,
∴Δ=(a+1)2-4(a-2)×=4a+1=0,
∴a=-,∴y=-x2+x-,易得其图像与坐标轴的交点坐标为和,符合题意.
(ii)当与y轴的交点是原点时,易得b=0,∵a=4b,∴a=0,∴y=-2x2+x,易得其图像与坐标轴的交点坐标为(0,0)和,符合题意.
故答案为0或2或-.
(2)如图所示,设直线l与BC交于点F,直线l与x轴交于点H.
将A,B点坐标代入解析式,
得
解得
∴抛物线的解析式为y=-x2+2x+8=-(x-1)2+9,
∴C(0,8).
①当点P为抛物线顶点时,P(1,9),
∴PH=9,xP=1,
由B(4,0),C(0,8)易得直线BC的解析式为y=-2x+8,
∵F在直线l上,∴F的横坐标等于P的横坐标,
∴xF=1,∵F在直线BC:y=-2x+8上,
∴F(1,6),∴FH=6,OH=1,
∴PF=PH-FH=9-6=3,BH=OB-OH=4-1=3,
∴S△PBC=S△PFC+S△PFB=xP·PF+HB·PF
=×1×3+×3×3=6,即△PBC的面积为6.
②S1-S2存在最大值.
易知OB=4,AO=2,AB=6,OC=8,AH=2+m,P(m,-m2+2m+8),
∴PH=-m2+2m+8,∵OD⊥x轴,PH⊥x轴,
∴OD∥PH,∴=,即=,
∴OD=8-2m.
∵S1=S△PBE=S△PAB-S△AOD-S四边形EDOB,S2=S△CDE=S△OBC-S四边形EDOB,
∴S1-S2=S△PAB-S△AOD-S△OBC=--=--=-3m2+8m=-3+,∵-3<0,0
3.解析 (1)将A(-3,0),B(6,0)的坐标代入y=ax2+bx-9,得解得
∴抛物线的表达式为y=x2-x-9.
(2)易知点C(0,-9),
设点P(m,0),点Q,在A,C,P,Q四点组成的平行四边形中,当AC为边,AQ为对角线时(如图1),
∵四边形ACQP为平行四边形,∴AP∥CQ,∴yQ=yC,∴n2-n-9=-9,解得n=0(舍去)或n=3,
∴点Q(3,-9).
在A,C,P,Q四点组成的平行四边形中,当AC为边,AP为对角线时(如图2),连接CQ,
线段CQ的中点在x轴上,∴yC+yQ=0,∴n2-n-9+(-9)=0,解得n=+或n=-,
∵yQ=-yC=9,
∴点Q的坐标为或.
综上,点Q的坐标为(3,-9)或或.
(3)设△PED的面积为S,
由题意得AP=m+3,BP=6-m,OB=6,OC=9,AB=9,∴BC==3,
∵sin∠PBD==,∴=,
∴PD=,
∵PE∥BC,∴△APE∽△ABC,∠EPD=∠PDB=90°,
∴=,∴=,∴PE=,
∴S=PE·PD=(m+3)(6-m)=-+,∴当m=时,S取得最大值,为,
∴当m=时,△PED的面积最大,为.
4.解析 (1)∵抛物线y=ax2+bx+4与x轴相交于点A(1,0),B(4,0),
∴解得
∴抛物线的表达式为y=x2-5x+4.
(2)易知C(0,4),抛物线的对称轴为直线x=.
∵△PAC的周长=PA+PC+AC,AC为定长,∴当PA+PC的值最小时,△PAC的周长最小,
∵点A,B关于对称轴对称,
∴PA+PC=PB+PC≥BC,故当P,B,C三点共线时,PA+PC的值最小,为BC的长,此时点P为直线BC与对称轴的交点,
由B(4,0),C(0,4)易得直线BC的解析式为y=-x+4,当x=时,y=-+4=,
∴P,∵A(1,0),C(0,4),
∴PA==,
PC==,∴=.
(3)存在.
∵D为OC的中点,∴D(0,2),∴OD=2,
∵B(4,0),∴OB=4,
在Rt△BOD中,tan∠OBD==,
∵tan∠QDB==tan∠OBD,∴∠QDB=∠OBD.
分情况讨论:①当Q点与D点在平行于x轴的直线上时,过点D作平行于x轴的直线,交抛物线于点Q1和Q2,如图,则∠Q1DB=∠OBD,此时点Q1,Q2的纵坐标为2,
设点Q1的横坐标为t1,点Q2的横坐标为t2,则t1,t2满足t2-5t+4=2,解得t1=,t2=,
∴Q1,Q2.
②当Q点在D点所在水平线的下方,即yQ
解得p=,∴E,
设直线DE的解析式为y=kx+q(k≠0),
代入D,E两点的坐标,
得解得∴y=-x+2,
联立抛物线与直线DE,得解得或∴Q3,Q4(3,-2).
综上,点Q的坐标为或或(3,-2)或.
方法解读 等角转化法:构造全等三角形、相似三角形,在这两类三角形中,对应角相等;由平行线的性质可知两直线平行,同位角相等,内错角相等;在同圆或等圆中,同弧或等弧所对的圆周角、圆心角相等;当两个锐角的三角函数值相等时,两锐角相等.我们常借助以上知识达到等角转化的目的.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
