第29章 直线与圆的位置关系素养综合检测试题(含解析)
文档属性
| 名称 | 第29章 直线与圆的位置关系素养综合检测试题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
第二十九章·素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
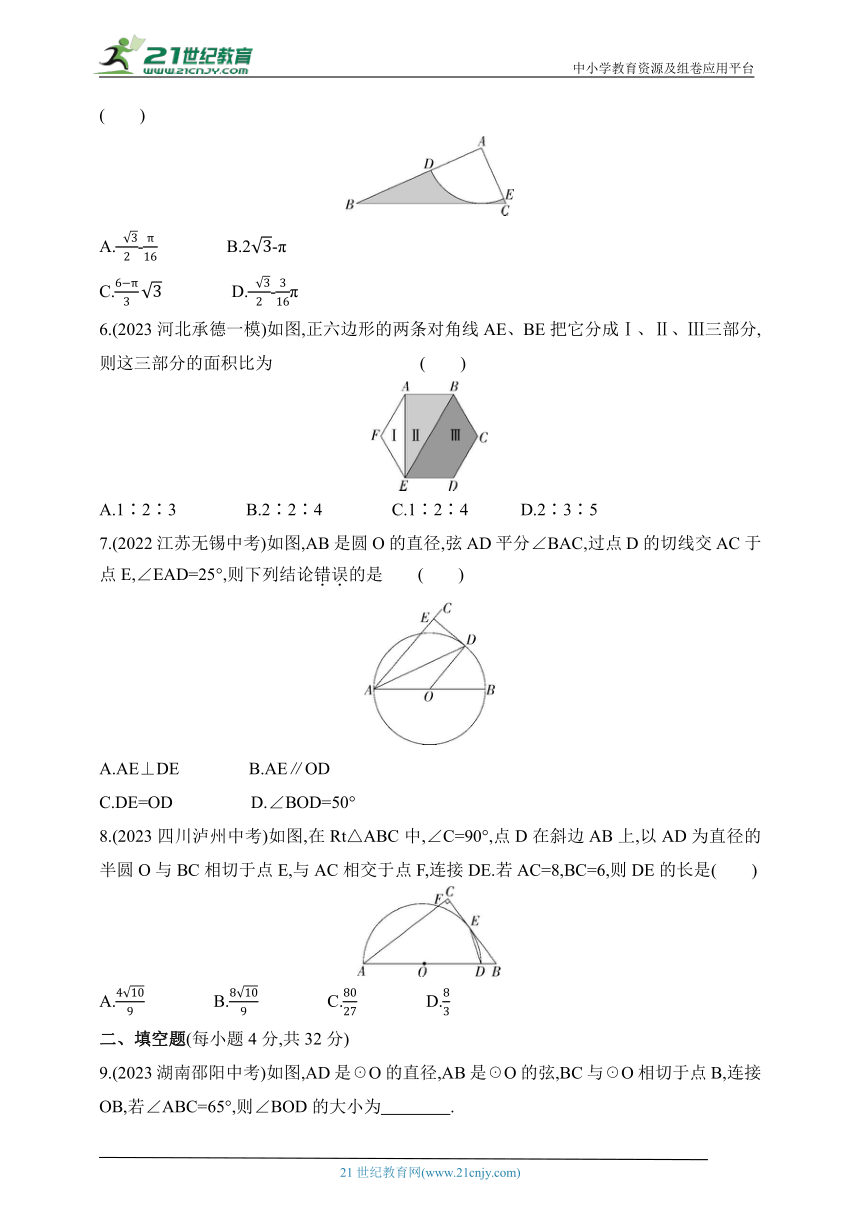
1.如图,矩形ABCD中,AB=4,BC=9,点E在边AD上,且AE=2ED,如果圆E是以点E为圆心,EC长为半径的圆,那么下列判断正确的是( )
A.点A,B均在圆E内
B.点B在圆E外,点A在圆E内
C.点B在圆E外,点A在圆E上
D.点A,B均在圆E外
2.(2023河北石家庄四十二中模拟)如图,已知点A、点C在☉O上,AB是☉O切线,连接AC,若∠ACO=65°,则∠CAB的度数为 ( )
A.35° B.30° C.25° D.20°
3.(2023山东临沂中考)将一个正六边形绕其中心旋转后仍与原图形重合,旋转角的大小不可能是 ( )
A.60° B.90° C.180° D.360°
4.(2023山东聊城中考)如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA.若∠CAI=35°,则∠OBC的度数为 ( )
A.15° B.17.5° C.20° D.25°
5.【新独家原创】如图,Rt△ABC中,∠A=90°,AB=,AC=1,以顶点A为圆心、以定长为半径画弧,交AB,AC于点D,E,恰好与BC边相切,则图中阴影部分的面积是 ( )
A.- B.2-π
C. D.-π
6.(2023河北承德一模)如图,正六边形的两条对角线AE、BE把它分成Ⅰ、Ⅱ、Ⅲ三部分,则这三部分的面积比为 ( )
A.1∶2∶3 B.2∶2∶4 C.1∶2∶4 D.2∶3∶5
7.(2022江苏无锡中考)如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是 ( )
A.AE⊥DE B.AE∥OD
C.DE=OD D.∠BOD=50°
8.(2023四川泸州中考)如图,在Rt△ABC中,∠C=90°,点D在斜边AB上,以AD为直径的半圆O与BC相切于点E,与AC相交于点F,连接DE.若AC=8,BC=6,则DE的长是( )
A. B. C. D.
二、填空题(每小题4分,共32分)
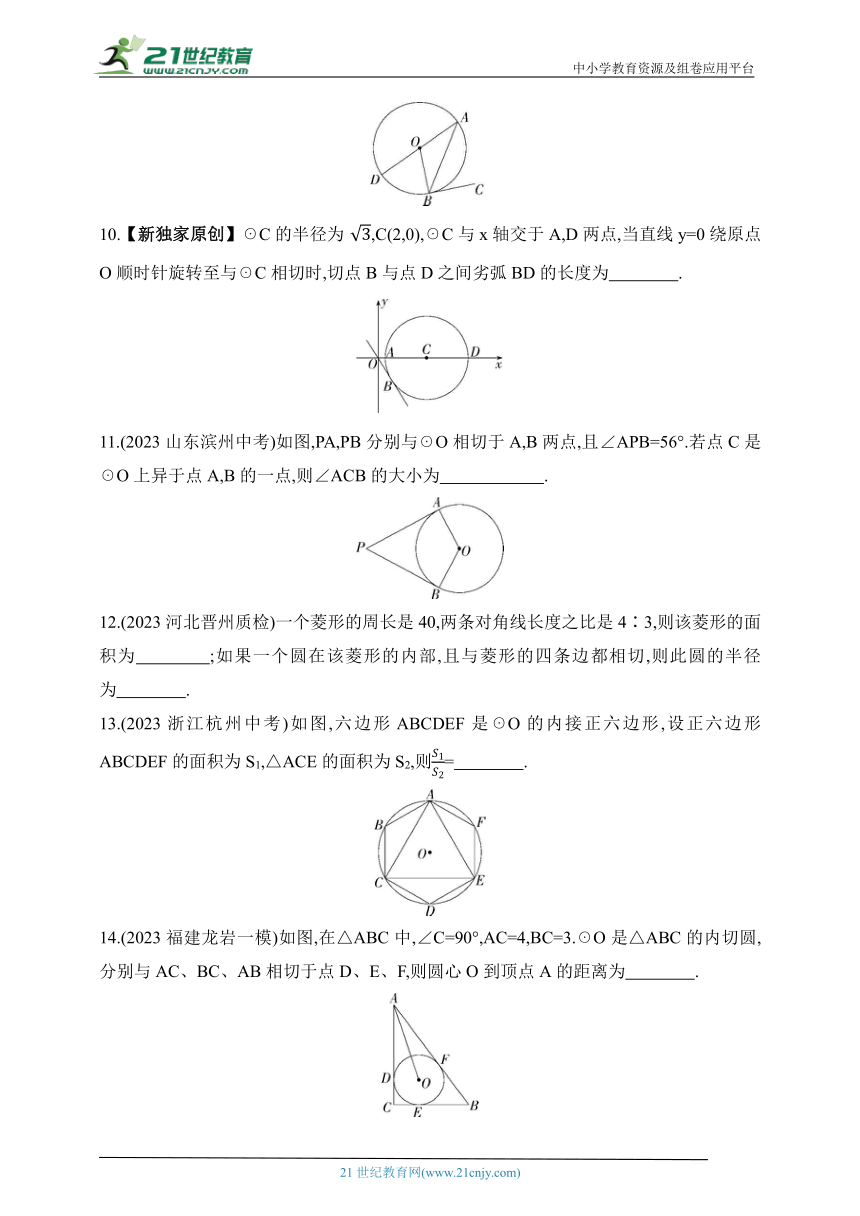
9.(2023湖南邵阳中考)如图,AD是☉O的直径,AB是☉O的弦,BC与☉O相切于点B,连接OB,若∠ABC=65°,则∠BOD的大小为 .
10.【新独家原创】☉C的半径为,C(2,0),☉C与x轴交于A,D两点,当直线y=0绕原点O顺时针旋转至与☉C相切时,切点B与点D之间劣弧BD的长度为 .
11.(2023山东滨州中考)如图,PA,PB分别与☉O相切于A,B两点,且∠APB=56°.若点C是☉O上异于点A,B的一点,则∠ACB的大小为 .
12.(2023河北晋州质检)一个菱形的周长是40,两条对角线长度之比是4∶3,则该菱形的面积为 ;如果一个圆在该菱形的内部,且与菱形的四条边都相切,则此圆的半径为 .
13.(2023浙江杭州中考)如图,六边形ABCDEF是☉O的内接正六边形,设正六边形ABCDEF的面积为S1,△ACE的面积为S2,则= .
14.(2023福建龙岩一模)如图,在△ABC中,∠C=90°,AC=4,BC=3.☉O是△ABC的内切圆,分别与AC、BC、AB相切于点D、E、F,则圆心O到顶点A的距离为 .
15.(2023山东济南天桥模拟)如图,正六边形ABCDEF的边长为2,以A为圆心,AC的长为半径画弧,得弧EC,连接AC,AE,则图中阴影部分的面积为 .
16.(2022四川宜宾中考)我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为 .
三、解答题(共36分)
17.(7分)如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.
(1)判断直线AD与圆O的位置关系,并说明理由;
(2)若圆O的半径为6,求图中阴影部分的面积.
18.(9分)如图,以四边形ABCD的对角线BD为直径作圆,圆心为O,过点A作AE⊥CD,交CD的延长线于点E,已知DA平分∠BDE.
(1)求证:AE是☉O的切线;
(2)若AE=4,CD=6,求☉O的半径和AD的长.
19.(2023北京门头沟一模)(10分)如图,AB是☉O的直径,点D在☉O上,连接AD并延长到C,使AC=AB,连接BC交☉O于E,过点B作☉O的切线交OE的延长线于点F.
(1)求证:OE∥AC;
(2)如果AB=10,AD=6,求EF的长.
20.(2023河北唐山一模)(10分)如图,已知△ABC是腰长为4的等腰直角三角形,∠ABC=90°,以A为圆心,2为半径作半圆A,交BA所在直线于点M,N.点E是半圆A上任意一点.连接BE,把BE绕点B顺时针旋转90°到BD的位置,连接AE,CD.
(1)求证:△EBA≌△DBC;
(2)当BE与半圆A相切时,求弧EM的长;
(3)直接写出△BCD面积的最大值.
答案全解全析
1.D ∵四边形ABCD为矩形,∴CD=AB=4,
∵AD=BC=9,AE=2ED,∴AE=6,DE=3.
在Rt△EDC中,EC==5,
在Rt△ABE中,EB==2,
∴EB>AE>EC,∴点A,B均在圆E外.故选D.
2.C 连接OA,则OA=OC,∴∠OAC=∠OCA=65°,
∵AB是☉O的切线,∴∠OAB=90°,
∴∠CAB=∠OAB-∠OAC=90°-65°=25°.故选C.
3.B 正六边形的中心角的度数为=60°,
∴正六边形绕其中心旋转60°或60°的整数倍时,仍与原图形重合,结合选项知旋转角的大小不可能是90°.故选B.
4.C 连接OC,∵点I是△ABC的内心,∠CAI=35°,
∴∠BAC=2∠CAI=70°,
∴∠BOC=2∠BAC=140°,∵OB=OC,
∴∠OBC=∠OCB==20°,故选C.
5.D 过点A作AF⊥BC,交BC于点F.∵BC为☉A的切线,∴AF为☉A的半径.
在Rt△ABC中,BC==2.
∵S△ABC=×AB×AC=×BC×AF,∴AF=,
∴S阴影=S△ABC-S扇形DAE=×1×-=-π.故选D.
6.A 如图,取BE的中点O,连接OA、OC、OD,则S△AFE=S△AOE=S△AOB=S△COB=S△COD=S△DOE,
∴Ⅰ、Ⅱ、Ⅲ三部分的面积比为1∶2∶3,故选A.
7.C ∵DE是☉O的切线,∴OD⊥DE,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠EAD,∴∠EAD=∠ODA,∴OD∥AE,∴AE⊥DE,故选项A、B结论都正确.
∵∠OAD=∠EAD=∠ODA=25°,∴∠BOD=∠OAD+∠ODA=50°,故选项D结论正确.
∵AD平分∠BAC,AE⊥DE,∴DE8.B 如图所示,连接OE,AE,
∵∠C=90°,AC=8,BC=6,∴AB==10,
∵以AD为直径的半圆O与BC相切于点E,∴OE⊥BC,∵∠C=90°,∴∠C=∠OEB=90°,
∴AC∥OE,∴∠CAB=∠EOB,∴△BCA∽△BEO,
∴==,即==,解得OE=,BE=,∴CE=BC-BE=,AD=2OE=,∴AE==,
∵AD是半圆O的直径,∴∠AED=90°,
∴DE==.故选B.
9.50°
解析 ∵BC与☉O相切于点B,∴∠OBC=90°,
∵∠ABC=65°,∴∠OBA=90°-65°=25°,
∵OB=OA,∴∠A=∠OBA=25°,
∴∠BOD=2×25°=50°.
10.
解析 连接BC,由题意知∠OBC=90°,在Rt△OBC中,OC=2,BC=,∴OB==1=OC,∴∠ACB=30°,∴∠DCB=150°,∴的长度==.
11.62°或118°
解析 如图所示,连接AC,BC,当点C在优弧AB上时,
∵PA,PB分别与☉O相切于A,B两点,∴∠PAO=∠PBO=90°,∵∠APB=56°,∴∠AOB=360°-90°-90°-56°=124°,
∴∠ACB=∠AOB=62°.
当点C'在劣弧AB上时,连接AC',BC',
∵四边形AC'BC是圆内接四边形,∴∠C'=180°-∠C=118°.故答案为62°或118°.
12.96;
解析 如图,E是AB与☉O的切点,连接OE,
设菱形的对角线BD=4a,AC=3a,
∵四边形ABCD是菱形,其周长为40,
∴AB=10,OB=2a,OA=a,AC⊥BD,
∴(2a)2+=102,
解得a=4(舍负),
∴BD=16,AC=12,∴菱形的面积为×16×12=96.
在Rt△ABO中,OE===,∴内切圆的半径为.
2
解析 如图所示,连接OA,OC,OE,
∵六边形ABCDEF是☉O的内接正六边形,∴AC=AE=CE,
∴△ACE是☉O的内接正三角形,∵∠B=120°,AB=BC,∴∠BAC=∠BCA=(180°-∠B)=30°,∵∠CAE=60°,∴∠OAC=∠OAE=30°,∴∠BAC=∠OAC=30°,同理可得,∠BCA=∠OCA=30°,又∵AC=AC,∴△BAC≌△OAC(ASA),∴S△BAC=S△OAC,
由圆和正六边形的性质可得S△BAC=S△AFE=S△CDE,
由圆和正三角形的性质可得S△OAC=S△OAE=S△OCE,
∵S1=S△BAC+S△AFE+S△CDE+S△OAC+S△OAE+S△OCE=2(S△OAC+S△OAE+S△OCE)=2S2,∴=2.
14.
解析 连接OD、OE、OF,如图,
由题意可得∠C=∠CDO=∠CEO=∠ADO=90°,OE=OD,AD=AF,CD=CE,BE=BF,则四边形ODCE为正方形,∴CD=OD,由勾股定理可得AB==5,设CD=CE=x,则AD=AF=4-x,BF=BE=3-x,∵AF+BF=AB=5,∴4-x+3-x=5,解得x=1,∴CD=OD=1,AD=4-1=3,由勾股定理可得AO==.
2π
解析 ∵正六边形ABCDEF的边长为2,∴AB=BC=2,∠ABC=∠BAF==120°,
∴∠BAC=∠BCA,∴∠BAC=(180°-∠ABC)=×(180°-120°)=30°,
过B作BH⊥AC于H(图略),
∴AH=CH,BH=AB=×2=1.
在Rt△ABH中,AH===,
∴AC=2.由对称性可知∠BAC=∠EAF=30°,
∴∠CAE=∠BAF-∠BAC-∠EAF=60°,
∴S扇形CAE==2π,即图中阴影部分的面积为2π.
16. 289
解析 设四个全等的直角三角形的三边长分别为a,b,c,较长的直角边长为a,较短的直角边长为b,c为斜边长.∵直角三角形的内切圆半径为3,小正方形的面积为49,∴=3,(a-b)2=49,∴a+b-c=6,a-b=7,∴a=,b=,∵a2+b2=c2,
∴+=c2,解得c=17或c=-5(舍去),
∴大正方形的面积为c2=172=289,故答案为289.
17.解析 (1)直线AD与圆O相切,理由如下:
如图,连接OA,∵AD∥BC,∴∠D=∠DBC,
∵AB=AD,∴∠D=∠ABD,
∵∠ABC=60°,∴∠DBC=∠ABD=∠D=30°,
∴∠BAD=120°,∵OA=OB,
∴∠BAO=∠ABD=30°,∴∠OAD=90°,∴OA⊥AD,
∵OA是圆O的半径,∴直线AD与圆O相切.
(2)如图,连接OC,过O点作OH⊥BC于H,∵OB=OC,∴∠OCB=∠OBC=30°,
∴∠BOC=180°-∠OBC-∠OCB=120°,OH=OB=3,
∴BH==3,∴BC=2BH=6,
∵扇形BOC的面积为=12π,
S△OBC=BC·OH=×6×3=9,
∴阴影部分的面积为S扇形BOC-S△BOC=12π-9.
18.解析 (1)证明:如图,连接OA,∵AE⊥CE,
∴∠DAE+∠ADE=90°.
∵DA平分∠BDE,
∴∠ADE=∠ADO.又∵OA=OD,
∴∠OAD=∠ADO=∠ADE,
∴∠DAE+∠OAD=90°,∴OA⊥AE,
∵OA是☉O的半径,∴AE是☉O的切线.
(2)如图,取CD的中点F,连接OF,∴OF⊥CD,
∴四边形AEFO是矩形.∵CD=6,∴DF=FC=3.在Rt△OFD中,OF=AE=4,∴OD===5,即☉O的半径为5.
在Rt△AED中,AE=4,ED=EF-DF=OA-DF=5-3=2,∴AD==2,即AD的长是2.
19.解析 (1)证明:∵AB=AC,∴∠C=∠ABC.
又∵OB=OE,∴∠OBE=∠OEB,∴∠OEB=∠C,
∴OE∥AC.
(2)连接BD,则∠ADB=90°,由AB=10可知☉O的半径为5,
∵OE∥AC,∴∠BAD=∠FOB.∵BF为☉O的切线,∴∠OBF=90°,∴∠OBF=∠ADB,∴△ADB∽△OBF,∴=,即=,∴OF=.∴EF=OF-OE=-5=,即EF的长是.
20.解析 (1)证明:由题意知BA=BC.由旋转可得∠EBD=90°,EB=DB,∴∠EBA+∠ABD=90°=∠DBC+∠ABD,∴∠EBA=∠DBC,
在△EBA与△DBC中,
∴△EBA≌△DBC.
(2)∵BE与半圆A相切,∴∠AEB=90°,
∵AB=4,AE=2,∴cos∠EAB==,∴∠EAB=60°,∴的长==π.
(3)4.
详解:根据题意,得点D在以点C为圆心,以2为半径的半圆上运动,
如图,过点D作DQ⊥BC于点Q,
∴S△BCD=BC·DQ=×4×DQ=2DQ,
当CD⊥BC时,DQ取得最大值,为2,
此时S△BCD=2DQ=2×2=4,即△BCD面积的最大值为4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
第二十九章·素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
1.如图,矩形ABCD中,AB=4,BC=9,点E在边AD上,且AE=2ED,如果圆E是以点E为圆心,EC长为半径的圆,那么下列判断正确的是( )
A.点A,B均在圆E内
B.点B在圆E外,点A在圆E内
C.点B在圆E外,点A在圆E上
D.点A,B均在圆E外
2.(2023河北石家庄四十二中模拟)如图,已知点A、点C在☉O上,AB是☉O切线,连接AC,若∠ACO=65°,则∠CAB的度数为 ( )
A.35° B.30° C.25° D.20°
3.(2023山东临沂中考)将一个正六边形绕其中心旋转后仍与原图形重合,旋转角的大小不可能是 ( )
A.60° B.90° C.180° D.360°
4.(2023山东聊城中考)如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA.若∠CAI=35°,则∠OBC的度数为 ( )
A.15° B.17.5° C.20° D.25°
5.【新独家原创】如图,Rt△ABC中,∠A=90°,AB=,AC=1,以顶点A为圆心、以定长为半径画弧,交AB,AC于点D,E,恰好与BC边相切,则图中阴影部分的面积是 ( )
A.- B.2-π
C. D.-π
6.(2023河北承德一模)如图,正六边形的两条对角线AE、BE把它分成Ⅰ、Ⅱ、Ⅲ三部分,则这三部分的面积比为 ( )
A.1∶2∶3 B.2∶2∶4 C.1∶2∶4 D.2∶3∶5
7.(2022江苏无锡中考)如图,AB是圆O的直径,弦AD平分∠BAC,过点D的切线交AC于点E,∠EAD=25°,则下列结论错误的是 ( )
A.AE⊥DE B.AE∥OD
C.DE=OD D.∠BOD=50°
8.(2023四川泸州中考)如图,在Rt△ABC中,∠C=90°,点D在斜边AB上,以AD为直径的半圆O与BC相切于点E,与AC相交于点F,连接DE.若AC=8,BC=6,则DE的长是( )
A. B. C. D.
二、填空题(每小题4分,共32分)
9.(2023湖南邵阳中考)如图,AD是☉O的直径,AB是☉O的弦,BC与☉O相切于点B,连接OB,若∠ABC=65°,则∠BOD的大小为 .
10.【新独家原创】☉C的半径为,C(2,0),☉C与x轴交于A,D两点,当直线y=0绕原点O顺时针旋转至与☉C相切时,切点B与点D之间劣弧BD的长度为 .
11.(2023山东滨州中考)如图,PA,PB分别与☉O相切于A,B两点,且∠APB=56°.若点C是☉O上异于点A,B的一点,则∠ACB的大小为 .
12.(2023河北晋州质检)一个菱形的周长是40,两条对角线长度之比是4∶3,则该菱形的面积为 ;如果一个圆在该菱形的内部,且与菱形的四条边都相切,则此圆的半径为 .
13.(2023浙江杭州中考)如图,六边形ABCDEF是☉O的内接正六边形,设正六边形ABCDEF的面积为S1,△ACE的面积为S2,则= .
14.(2023福建龙岩一模)如图,在△ABC中,∠C=90°,AC=4,BC=3.☉O是△ABC的内切圆,分别与AC、BC、AB相切于点D、E、F,则圆心O到顶点A的距离为 .
15.(2023山东济南天桥模拟)如图,正六边形ABCDEF的边长为2,以A为圆心,AC的长为半径画弧,得弧EC,连接AC,AE,则图中阴影部分的面积为 .
16.(2022四川宜宾中考)我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为 .
三、解答题(共36分)
17.(7分)如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.
(1)判断直线AD与圆O的位置关系,并说明理由;
(2)若圆O的半径为6,求图中阴影部分的面积.
18.(9分)如图,以四边形ABCD的对角线BD为直径作圆,圆心为O,过点A作AE⊥CD,交CD的延长线于点E,已知DA平分∠BDE.
(1)求证:AE是☉O的切线;
(2)若AE=4,CD=6,求☉O的半径和AD的长.
19.(2023北京门头沟一模)(10分)如图,AB是☉O的直径,点D在☉O上,连接AD并延长到C,使AC=AB,连接BC交☉O于E,过点B作☉O的切线交OE的延长线于点F.
(1)求证:OE∥AC;
(2)如果AB=10,AD=6,求EF的长.
20.(2023河北唐山一模)(10分)如图,已知△ABC是腰长为4的等腰直角三角形,∠ABC=90°,以A为圆心,2为半径作半圆A,交BA所在直线于点M,N.点E是半圆A上任意一点.连接BE,把BE绕点B顺时针旋转90°到BD的位置,连接AE,CD.
(1)求证:△EBA≌△DBC;
(2)当BE与半圆A相切时,求弧EM的长;
(3)直接写出△BCD面积的最大值.
答案全解全析
1.D ∵四边形ABCD为矩形,∴CD=AB=4,
∵AD=BC=9,AE=2ED,∴AE=6,DE=3.
在Rt△EDC中,EC==5,
在Rt△ABE中,EB==2,
∴EB>AE>EC,∴点A,B均在圆E外.故选D.
2.C 连接OA,则OA=OC,∴∠OAC=∠OCA=65°,
∵AB是☉O的切线,∴∠OAB=90°,
∴∠CAB=∠OAB-∠OAC=90°-65°=25°.故选C.
3.B 正六边形的中心角的度数为=60°,
∴正六边形绕其中心旋转60°或60°的整数倍时,仍与原图形重合,结合选项知旋转角的大小不可能是90°.故选B.
4.C 连接OC,∵点I是△ABC的内心,∠CAI=35°,
∴∠BAC=2∠CAI=70°,
∴∠BOC=2∠BAC=140°,∵OB=OC,
∴∠OBC=∠OCB==20°,故选C.
5.D 过点A作AF⊥BC,交BC于点F.∵BC为☉A的切线,∴AF为☉A的半径.
在Rt△ABC中,BC==2.
∵S△ABC=×AB×AC=×BC×AF,∴AF=,
∴S阴影=S△ABC-S扇形DAE=×1×-=-π.故选D.
6.A 如图,取BE的中点O,连接OA、OC、OD,则S△AFE=S△AOE=S△AOB=S△COB=S△COD=S△DOE,
∴Ⅰ、Ⅱ、Ⅲ三部分的面积比为1∶2∶3,故选A.
7.C ∵DE是☉O的切线,∴OD⊥DE,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠EAD,∴∠EAD=∠ODA,∴OD∥AE,∴AE⊥DE,故选项A、B结论都正确.
∵∠OAD=∠EAD=∠ODA=25°,∴∠BOD=∠OAD+∠ODA=50°,故选项D结论正确.
∵AD平分∠BAC,AE⊥DE,∴DE
∵∠C=90°,AC=8,BC=6,∴AB==10,
∵以AD为直径的半圆O与BC相切于点E,∴OE⊥BC,∵∠C=90°,∴∠C=∠OEB=90°,
∴AC∥OE,∴∠CAB=∠EOB,∴△BCA∽△BEO,
∴==,即==,解得OE=,BE=,∴CE=BC-BE=,AD=2OE=,∴AE==,
∵AD是半圆O的直径,∴∠AED=90°,
∴DE==.故选B.
9.50°
解析 ∵BC与☉O相切于点B,∴∠OBC=90°,
∵∠ABC=65°,∴∠OBA=90°-65°=25°,
∵OB=OA,∴∠A=∠OBA=25°,
∴∠BOD=2×25°=50°.
10.
解析 连接BC,由题意知∠OBC=90°,在Rt△OBC中,OC=2,BC=,∴OB==1=OC,∴∠ACB=30°,∴∠DCB=150°,∴的长度==.
11.62°或118°
解析 如图所示,连接AC,BC,当点C在优弧AB上时,
∵PA,PB分别与☉O相切于A,B两点,∴∠PAO=∠PBO=90°,∵∠APB=56°,∴∠AOB=360°-90°-90°-56°=124°,
∴∠ACB=∠AOB=62°.
当点C'在劣弧AB上时,连接AC',BC',
∵四边形AC'BC是圆内接四边形,∴∠C'=180°-∠C=118°.故答案为62°或118°.
12.96;
解析 如图,E是AB与☉O的切点,连接OE,
设菱形的对角线BD=4a,AC=3a,
∵四边形ABCD是菱形,其周长为40,
∴AB=10,OB=2a,OA=a,AC⊥BD,
∴(2a)2+=102,
解得a=4(舍负),
∴BD=16,AC=12,∴菱形的面积为×16×12=96.
在Rt△ABO中,OE===,∴内切圆的半径为.
2
解析 如图所示,连接OA,OC,OE,
∵六边形ABCDEF是☉O的内接正六边形,∴AC=AE=CE,
∴△ACE是☉O的内接正三角形,∵∠B=120°,AB=BC,∴∠BAC=∠BCA=(180°-∠B)=30°,∵∠CAE=60°,∴∠OAC=∠OAE=30°,∴∠BAC=∠OAC=30°,同理可得,∠BCA=∠OCA=30°,又∵AC=AC,∴△BAC≌△OAC(ASA),∴S△BAC=S△OAC,
由圆和正六边形的性质可得S△BAC=S△AFE=S△CDE,
由圆和正三角形的性质可得S△OAC=S△OAE=S△OCE,
∵S1=S△BAC+S△AFE+S△CDE+S△OAC+S△OAE+S△OCE=2(S△OAC+S△OAE+S△OCE)=2S2,∴=2.
14.
解析 连接OD、OE、OF,如图,
由题意可得∠C=∠CDO=∠CEO=∠ADO=90°,OE=OD,AD=AF,CD=CE,BE=BF,则四边形ODCE为正方形,∴CD=OD,由勾股定理可得AB==5,设CD=CE=x,则AD=AF=4-x,BF=BE=3-x,∵AF+BF=AB=5,∴4-x+3-x=5,解得x=1,∴CD=OD=1,AD=4-1=3,由勾股定理可得AO==.
2π
解析 ∵正六边形ABCDEF的边长为2,∴AB=BC=2,∠ABC=∠BAF==120°,
∴∠BAC=∠BCA,∴∠BAC=(180°-∠ABC)=×(180°-120°)=30°,
过B作BH⊥AC于H(图略),
∴AH=CH,BH=AB=×2=1.
在Rt△ABH中,AH===,
∴AC=2.由对称性可知∠BAC=∠EAF=30°,
∴∠CAE=∠BAF-∠BAC-∠EAF=60°,
∴S扇形CAE==2π,即图中阴影部分的面积为2π.
16. 289
解析 设四个全等的直角三角形的三边长分别为a,b,c,较长的直角边长为a,较短的直角边长为b,c为斜边长.∵直角三角形的内切圆半径为3,小正方形的面积为49,∴=3,(a-b)2=49,∴a+b-c=6,a-b=7,∴a=,b=,∵a2+b2=c2,
∴+=c2,解得c=17或c=-5(舍去),
∴大正方形的面积为c2=172=289,故答案为289.
17.解析 (1)直线AD与圆O相切,理由如下:
如图,连接OA,∵AD∥BC,∴∠D=∠DBC,
∵AB=AD,∴∠D=∠ABD,
∵∠ABC=60°,∴∠DBC=∠ABD=∠D=30°,
∴∠BAD=120°,∵OA=OB,
∴∠BAO=∠ABD=30°,∴∠OAD=90°,∴OA⊥AD,
∵OA是圆O的半径,∴直线AD与圆O相切.
(2)如图,连接OC,过O点作OH⊥BC于H,∵OB=OC,∴∠OCB=∠OBC=30°,
∴∠BOC=180°-∠OBC-∠OCB=120°,OH=OB=3,
∴BH==3,∴BC=2BH=6,
∵扇形BOC的面积为=12π,
S△OBC=BC·OH=×6×3=9,
∴阴影部分的面积为S扇形BOC-S△BOC=12π-9.
18.解析 (1)证明:如图,连接OA,∵AE⊥CE,
∴∠DAE+∠ADE=90°.
∵DA平分∠BDE,
∴∠ADE=∠ADO.又∵OA=OD,
∴∠OAD=∠ADO=∠ADE,
∴∠DAE+∠OAD=90°,∴OA⊥AE,
∵OA是☉O的半径,∴AE是☉O的切线.
(2)如图,取CD的中点F,连接OF,∴OF⊥CD,
∴四边形AEFO是矩形.∵CD=6,∴DF=FC=3.在Rt△OFD中,OF=AE=4,∴OD===5,即☉O的半径为5.
在Rt△AED中,AE=4,ED=EF-DF=OA-DF=5-3=2,∴AD==2,即AD的长是2.
19.解析 (1)证明:∵AB=AC,∴∠C=∠ABC.
又∵OB=OE,∴∠OBE=∠OEB,∴∠OEB=∠C,
∴OE∥AC.
(2)连接BD,则∠ADB=90°,由AB=10可知☉O的半径为5,
∵OE∥AC,∴∠BAD=∠FOB.∵BF为☉O的切线,∴∠OBF=90°,∴∠OBF=∠ADB,∴△ADB∽△OBF,∴=,即=,∴OF=.∴EF=OF-OE=-5=,即EF的长是.
20.解析 (1)证明:由题意知BA=BC.由旋转可得∠EBD=90°,EB=DB,∴∠EBA+∠ABD=90°=∠DBC+∠ABD,∴∠EBA=∠DBC,
在△EBA与△DBC中,
∴△EBA≌△DBC.
(2)∵BE与半圆A相切,∴∠AEB=90°,
∵AB=4,AE=2,∴cos∠EAB==,∴∠EAB=60°,∴的长==π.
(3)4.
详解:根据题意,得点D在以点C为圆心,以2为半径的半圆上运动,
如图,过点D作DQ⊥BC于点Q,
∴S△BCD=BC·DQ=×4×DQ=2DQ,
当CD⊥BC时,DQ取得最大值,为2,
此时S△BCD=2DQ=2×2=4,即△BCD面积的最大值为4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
