第32章 投影与视图素养综合检测试题(含解析)
文档属性
| 名称 | 第32章 投影与视图素养综合检测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 797.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 17:58:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
第三十二章·素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
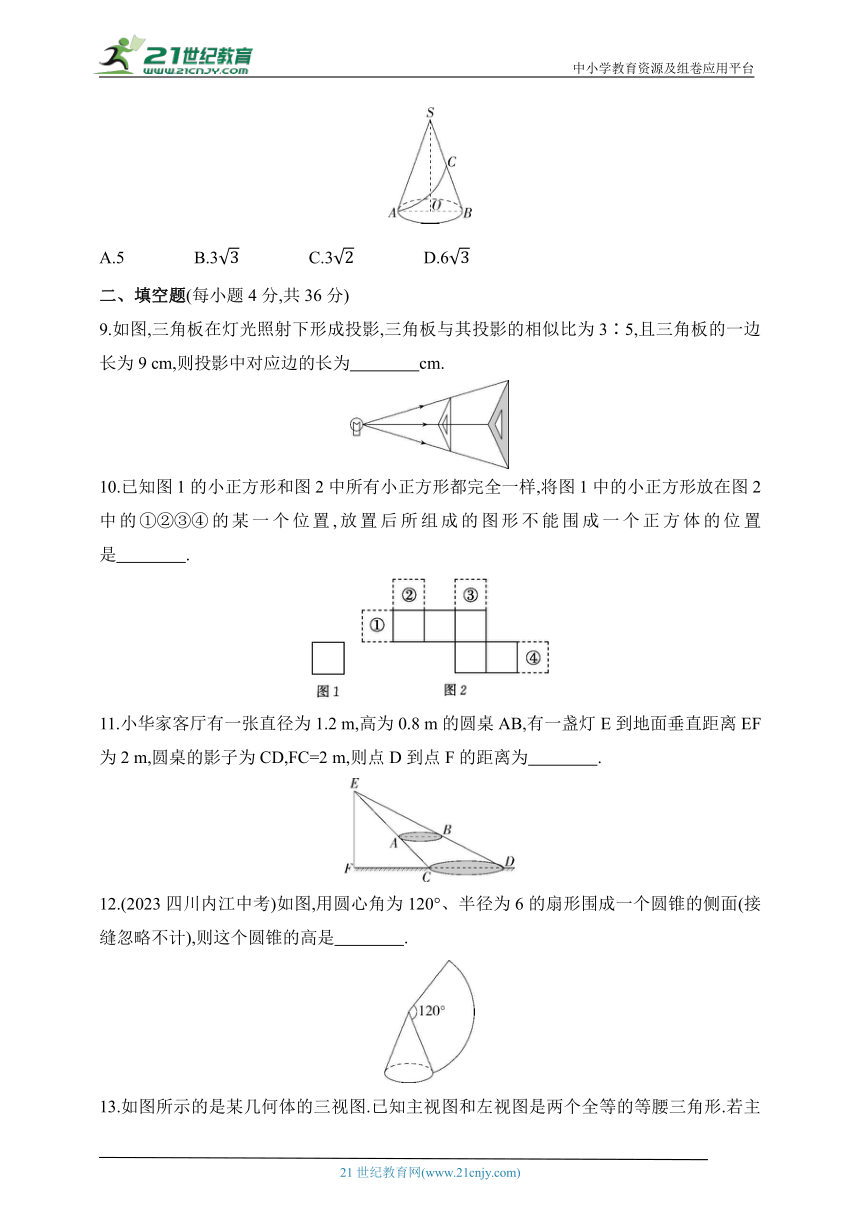
1.(2023湖南衡阳中考)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.下图是一把做工精湛的紫砂壶“景舟石瓢”,其左视图的大致形状是 ( )
2.(2023江苏连云港中考)下列水平放置的几何体中,主视图是圆形的
是 ( )
3.(2023安徽中考)某几何体的三视图如图所示,则该几何体为 ( )
4.(2023四川凉山州中考) 如图所示的是由4个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是 ( )
A B C D
5.(2023湖北荆州中考)观察如图所示的几何体,下列关于其三视图的说法正确的是 ( )
A.主视图既是中心对称图形,又是轴对称图形
B.左视图既是中心对称图形,又是轴对称图形
C.俯视图既是中心对称图形,又是轴对称图形
D.主视图、左视图、俯视图都是中心对称图形
6.(2023河北武邑二模)如图所示的正方体,它的展开图可能是下列四个选项中的 ( )
A B
C D
7.(2023河北中考)如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至少还需再放这样的正方体 ( )
图1 图2
A.1个 B.2个 C.3个 D.4个
8.(2023湖北十堰中考)如图,已知点C为圆锥母线SB的中点,AB为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为 ( )
A.5 B.3 C.3 D.6
二、填空题(每小题4分,共36分)
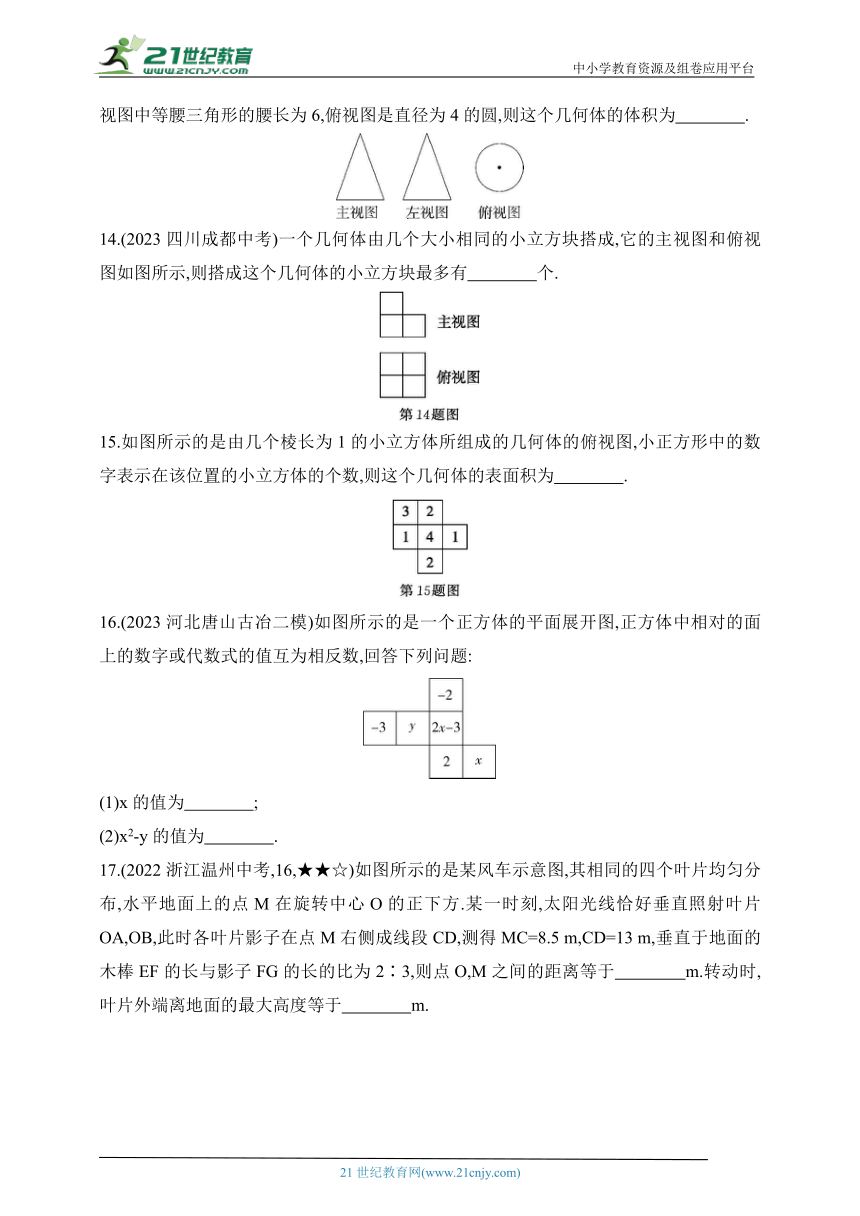
9.如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为3∶5,且三角板的一边长为9 cm,则投影中对应边的长为 cm.
10.已知图1的小正方形和图2中所有小正方形都完全一样,将图1中的小正方形放在图2中的①②③④的某一个位置,放置后所组成的图形不能围成一个正方体的位置是 .
11.小华家客厅有一张直径为1.2 m,高为0.8 m的圆桌AB,有一盏灯E到地面垂直距离EF为2 m,圆桌的影子为CD,FC=2 m,则点D到点F的距离为 .
12.(2023四川内江中考)如图,用圆心角为120°、半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是 .
13.如图所示的是某几何体的三视图.已知主视图和左视图是两个全等的等腰三角形.若主视图中等腰三角形的腰长为6,俯视图是直径为4的圆,则这个几何体的体积为 .
14.(2023四川成都中考)一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有 个.
15.如图所示的是由几个棱长为1的小立方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,则这个几何体的表面积为 .
16.(2023河北唐山古冶二模)如图所示的是一个正方体的平面展开图,正方体中相对的面上的数字或代数式的值互为相反数,回答下列问题:
(1)x的值为 ;
(2)x2-y的值为 .
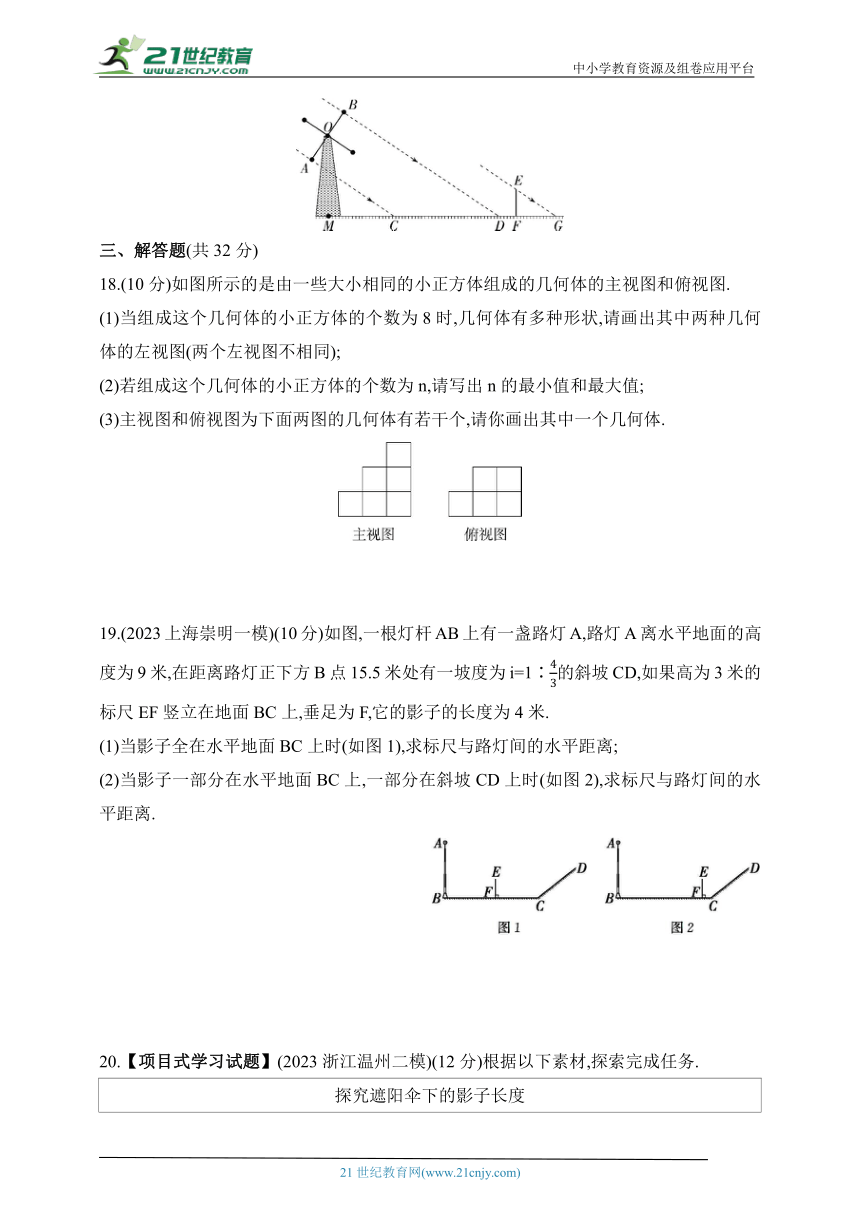
17.(2022浙江温州中考,16,★★☆)如图所示的是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片OA,OB,此时各叶片影子在点M右侧成线段CD,测得MC=8.5 m,CD=13 m,垂直于地面的木棒EF的长与影子FG的长的比为2∶3,则点O,M之间的距离等于 m.转动时,叶片外端离地面的最大高度等于 m.
三、解答题(共32分)
18.(10分)如图所示的是由一些大小相同的小正方体组成的几何体的主视图和俯视图.
(1)当组成这个几何体的小正方体的个数为8时,几何体有多种形状,请画出其中两种几何体的左视图(两个左视图不相同);
(2)若组成这个几何体的小正方体的个数为n,请写出n的最小值和最大值;
(3)主视图和俯视图为下面两图的几何体有若干个,请你画出其中一个几何体.
19.(2023上海崇明一模)(10分)如图,一根灯杆AB上有一盏路灯A,路灯A离水平地面的高度为9米,在距离路灯正下方B点15.5米处有一坡度为i=1∶的斜坡CD,如果高为3米的标尺EF竖立在地面BC上,垂足为F,它的影子的长度为4米.
(1)当影子全在水平地面BC上时(如图1),求标尺与路灯间的水平距离;
(2)当影子一部分在水平地面BC上,一部分在斜坡CD上时(如图2),求标尺与路灯间的水平距离.
20.【项目式学习试题】(2023浙江温州二模)(12分)根据以下素材,探索完成任务.
探究遮阳伞下的影子长度
素 材 1 图1是某款自动旋转遮阳伞,伞面完全张开时张角呈180°,图2是其侧面示意图.已知支架AB长为2.5米,且垂直于地面BC,悬托架AE=DE=0.5米,点E固定在伞面上,且伞面直径DF是DE的4倍.当伞面完全张开时,点D,E,F始终共线.为实现遮阳效果最佳,伞面装有接收器可以根据太阳光线的角度变化,自动调整手柄D沿着AB移动,以保证太阳光线与DF始终垂直
素 材 2 某地区某天下午不同时间的太阳高度角α(太阳光线与地面的夹角)参照表如下: 时刻12点13点14点15点16点17点太阳高度角α90°75°60°45°30°15°
素 材 3 小明坐在露营椅上的高度(头顶到地面的距离)约为1米.小明坐的位置记为点Q,如图2. 参考数据:≈1.7,≈1.4
问题解决
任 务 1 确定影子长度 某一时刻测得BD=1.7米,请求出此时影子GH的长度
任 务 2 判断是否照射到 这天14点,小明坐在离支架3米处的Q点,请判断此时小明是否被太阳光照射到
续表
任 务 3 探究合理范围 小明打算在这天14:00-15:00露营休息,为保证小明全程不被太阳光照射到,请计算BQ的取值范围
答案全解全析
1.B A.是从上向下看得到的图形,为俯视图,故选项A不合题意;
B.是从左向右看得到的图形,为左视图,故选项B符合题意;
C.不是该实物的视图,故选项C不合题意;
D.是从前往后看得到的图形,是主视图,故选项D不合题意.故选B.
2.C A.主视图是等腰三角形,故此选项不合题意;B.主视图是梯形,故此选项不合题意;C.主视图是圆,故此选项符合题意;D.主视图是矩形,故此选项不合题意.故选C.
3.B 主视图是直角三角形,故A,C,D选项不合题意,故选B.
4.B 由俯视图可得主视图有2列,左边一列有2个小正方形,右边一列有1个小正方形.故选B.
5.C 主视图和左视图相同,都是由上下两个等腰三角形组成的,不是中心对称图形,是轴对称图形.俯视图是圆(带圆心),既是中心对称图形,又是轴对称图形,故选C.
6.C 根据正方体的平面展开图的特征,可知A、B选项折叠后“数”字所在面和“好”字所在面是相对面,不符合题意;D选项折叠后“数”在上面,“好”在右面时,“学”却在背面,与题干图不一致,不符合题意.故选C.
7.B 由题意画出草图,如图,平台上至少还需再放这样的正方体2个,故选B.
8.B ∵AB为底面圆的直径,AB=4,
∴底面圆周长为4π,
圆锥的侧面展开图如图所示,连接AB,
设圆锥的侧面展开后扇形的圆心角为n,
∴4π=,解得n=120°,∴∠ASC=60°,
∵SA=SB,∴△SAB是等边三角形,∵C为SB的中点,∴AC⊥SB.在Rt△ACS中,AC=SA·sin 60°=6×=3,∴蚂蚁爬行的最短路程为3,故选B.
9.15
解析 设投影中对应边的长为x cm,∵三角板与其投影相似,∴对应边之比等于相似比,∴9∶x=3∶5,解得x=15.故答案是15.
10. ①
解析 根据正方体展开图的特征,可知②③④位置都是可以的,只有①不可以,故答案为①.
11.4 m
解析 ∵AB∥CD,∴△ABE∽△CDE,∵相似三角形对应边之比等于对应高之比,∴=.
∵AB=1.2,∴CD=2.又∵FC=2,∴DF=CD+FC=2+2=4(m).故答案为4 m.
12.4
解析 圆心角为120°、半径为6的扇形弧长==4π,
设圆锥底面圆的半径为r,则2πr=4π,解得r=2.
如图,圆锥高OD,底面圆半径DC,与母线OC构成直角三角形,由勾股定理得OD===4,故这个圆锥的高是4.
13.
解析 根据三视图可知这个几何体是圆锥,
圆锥的高为=4,
∴V=π××4=,故答案为.
14.6
解析 根据主视图和俯视图可得该几何体第一层(最底层)有4个小立方块,第二层最多有2个小立方块,∴搭成这个几何体的小立方块最多有4+2=6个,故答案为6.
15.46
解析 这个几何体的主视图有三列,从左到右分别有3,4,1个小正方形,左视图有三列,从左到右分别有3,4,2个小正方形,俯视图有6个小正方形,故几何体表面积为(8+9+6)×2×12=46,故答案为46.
16.(1)3 (2)12
解析 (1)正方体的表面展开图,相对的面之间一定相隔一个正方形,“-3”所在面与“2x-3”所在面是相对面,“y”所在面与“x”所在面是相对面.
∵相对面上的数字或代数式的值互为相反数,
∴2x-3+(-3)=0,x+y=0,解得x=3,y=-3,
故答案是3.
(2)当x=3,y=-3时,x2-y=32-(-3)=12,
故答案是12.
17. 10;(10+)
解析 如图,过点O作AC,BD的平行线,交CD于H,过点O作OJ∥MH交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO到点K,使得OK=OB.
由题意可知点O是AB的中点,∠BJI=∠EGF,
∴△BIJ∽△EFG.
∵OH∥AC∥BD,AO=BO,
∴点H是CD的中点,
∵CD=13 m,∴CH=HD=CD=6.5 m,
∴MH=MC+CH=8.5+6.5=15 m,
由题意可知==,∴=,
解得OM=10 m,∴点O,M之间的距离等于10 m.
∵BI⊥OJ,∴∠BIO=∠BIJ=90°,
由题意可知∠OBJ=∠OBI+∠JBI=90°,
又∵∠BOI+∠OBI=90°,
∴∠BOI=∠JBI,
∴△BOI∽△JBI,∴===,
∴BI=IJ,OI=BI=IJ,
∵OJ∥CD,OH∥DJ,
∴四边形OHDJ是平行四边形,
∴OJ=HD=6.5 m,∵OJ=OI+IJ=IJ+IJ=6.5 m,
∴IJ=4.5 m,∴BI=3 m,OI=2 m,
∵在Rt△OBI中,由勾股定理得OB2=OI2+BI2,
∴OB===(m),
∴OB=OK= m,
∴MK=MO+OK=(10+)m,
∴叶片外端离地面的最大高度等于(10+)m.
故答案为10;(10+).
18.解析 (1)如图所示(下图中的任意两个均可):
(2)∵俯视图有5个正方形,
∴最底层有5个正方体.
由主视图可得第2层最少有2个正方体,第3层最少有1个正方体;由主视图可得第2层最多有4个正方体,第3层最多有2个正方体.
∴该几何体最少有5+2+1=8个正方体,最多有5+4+2=11个正方体,∴n的最小值为8,最大值为11.
(3)如图所示(答案不唯一).
19.解析 (1)如图1,
由题意可知AB⊥BC,EF⊥BC,
∴AB∥EF,∴△EFG∽△ABG,
∴=.
由题意可知EF=3米,AB=9米,FG=4米,
∴=,解得BF=8,即标尺与路灯间的水平距离为8米.
(2)如图2,连接AE交CD于点M,过点M作MN⊥BC交BC延长线于点N,过点M作MG⊥AB于点G,交EF于点H,
∵影子长为4米,∴FC+CM=4米,设CM=x米,
∴FC=(4-x)米,∵AB⊥BC,EF⊥BC,∴AB∥EF,
∴△AGM∽△EHM,∴=,∵CM=x米,=,∴CN=x米,MN=x米,∴HF=GB=MN=x米,GM=BN=BC+CN=米,HM=FN=FC+CN=米,∴AG=AB-BG=米,EH=EF-HF=米,
∴=,
∴2x2+9x-35=0,解得x1=-7(不合题意,舍去),
x2=,经检验,x=是分式方程的解且符合题意,
∴FC=4-x=米,∴BF=15.5-=14米,即标尺与路灯间的水平距离为14米.
20.解析 任务1:如图1,过点E作EI⊥AB于点I,过点G作GJ⊥FH于点J,易知∠DGB=∠JHB=∠α.
∵BD=1.7,AB=2.5,∴AD=0.8,
∵AE=DE=0.5,
∴DF=4DE=2,DI=AD=0.4,
在Rt△EID中,EI==0.3,
∴sin∠IDE==.
∵∠FDG=∠DBG=90°,
∴∠IDE+∠BDG=90°,∠BDG+∠DGB=90°,
∴∠IDE=∠DGB=∠JHB=∠α.
易得四边形DGJF为矩形,
∴GJ=DF=2,
在Rt△GJH中,GH===2×=(米).
任务2:解法一:如图2,过点Q作QP⊥BC交HF于点P.由(1)知,∠IDE=∠α=∠DGB.
∵∠α=60°,∴在Rt△IDE中,DI=DE=,
∴AD=2DI=,∴BD=AB-AD=2.
在Rt△DBG中,BG===,
在Rt△GJH中,GH===.
在Rt△PQH中,当PQ=1时,QH===,
∴小明刚好被照射到时离B点的距离为BG+GH-QH=+-=.∵<3,∴小明会被照射到.
解法二:如图2,过点Q作QP⊥BC交FH于点P.与解法一同理得BG=,GH=,
∴QH=BH-BQ=2-3.在Rt△PQH中,PQ=QH·tan∠α=6-3<1,∴小明会被照射到.
任务3:当tan α=45°时,BQ取得最小值,也即为∠α=45°时BG的长度.由(2)的解法同理可求BQ=BG=.
当tan α=60°时,BQ取得最大值,为=.
∴21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
第三十二章·素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
1.(2023湖南衡阳中考)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.下图是一把做工精湛的紫砂壶“景舟石瓢”,其左视图的大致形状是 ( )
2.(2023江苏连云港中考)下列水平放置的几何体中,主视图是圆形的
是 ( )
3.(2023安徽中考)某几何体的三视图如图所示,则该几何体为 ( )
4.(2023四川凉山州中考) 如图所示的是由4个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是 ( )
A B C D
5.(2023湖北荆州中考)观察如图所示的几何体,下列关于其三视图的说法正确的是 ( )
A.主视图既是中心对称图形,又是轴对称图形
B.左视图既是中心对称图形,又是轴对称图形
C.俯视图既是中心对称图形,又是轴对称图形
D.主视图、左视图、俯视图都是中心对称图形
6.(2023河北武邑二模)如图所示的正方体,它的展开图可能是下列四个选项中的 ( )
A B
C D
7.(2023河北中考)如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至少还需再放这样的正方体 ( )
图1 图2
A.1个 B.2个 C.3个 D.4个
8.(2023湖北十堰中考)如图,已知点C为圆锥母线SB的中点,AB为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为 ( )
A.5 B.3 C.3 D.6
二、填空题(每小题4分,共36分)
9.如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为3∶5,且三角板的一边长为9 cm,则投影中对应边的长为 cm.
10.已知图1的小正方形和图2中所有小正方形都完全一样,将图1中的小正方形放在图2中的①②③④的某一个位置,放置后所组成的图形不能围成一个正方体的位置是 .
11.小华家客厅有一张直径为1.2 m,高为0.8 m的圆桌AB,有一盏灯E到地面垂直距离EF为2 m,圆桌的影子为CD,FC=2 m,则点D到点F的距离为 .
12.(2023四川内江中考)如图,用圆心角为120°、半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是 .
13.如图所示的是某几何体的三视图.已知主视图和左视图是两个全等的等腰三角形.若主视图中等腰三角形的腰长为6,俯视图是直径为4的圆,则这个几何体的体积为 .
14.(2023四川成都中考)一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如图所示,则搭成这个几何体的小立方块最多有 个.
15.如图所示的是由几个棱长为1的小立方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,则这个几何体的表面积为 .
16.(2023河北唐山古冶二模)如图所示的是一个正方体的平面展开图,正方体中相对的面上的数字或代数式的值互为相反数,回答下列问题:
(1)x的值为 ;
(2)x2-y的值为 .
17.(2022浙江温州中考,16,★★☆)如图所示的是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片OA,OB,此时各叶片影子在点M右侧成线段CD,测得MC=8.5 m,CD=13 m,垂直于地面的木棒EF的长与影子FG的长的比为2∶3,则点O,M之间的距离等于 m.转动时,叶片外端离地面的最大高度等于 m.
三、解答题(共32分)
18.(10分)如图所示的是由一些大小相同的小正方体组成的几何体的主视图和俯视图.
(1)当组成这个几何体的小正方体的个数为8时,几何体有多种形状,请画出其中两种几何体的左视图(两个左视图不相同);
(2)若组成这个几何体的小正方体的个数为n,请写出n的最小值和最大值;
(3)主视图和俯视图为下面两图的几何体有若干个,请你画出其中一个几何体.
19.(2023上海崇明一模)(10分)如图,一根灯杆AB上有一盏路灯A,路灯A离水平地面的高度为9米,在距离路灯正下方B点15.5米处有一坡度为i=1∶的斜坡CD,如果高为3米的标尺EF竖立在地面BC上,垂足为F,它的影子的长度为4米.
(1)当影子全在水平地面BC上时(如图1),求标尺与路灯间的水平距离;
(2)当影子一部分在水平地面BC上,一部分在斜坡CD上时(如图2),求标尺与路灯间的水平距离.
20.【项目式学习试题】(2023浙江温州二模)(12分)根据以下素材,探索完成任务.
探究遮阳伞下的影子长度
素 材 1 图1是某款自动旋转遮阳伞,伞面完全张开时张角呈180°,图2是其侧面示意图.已知支架AB长为2.5米,且垂直于地面BC,悬托架AE=DE=0.5米,点E固定在伞面上,且伞面直径DF是DE的4倍.当伞面完全张开时,点D,E,F始终共线.为实现遮阳效果最佳,伞面装有接收器可以根据太阳光线的角度变化,自动调整手柄D沿着AB移动,以保证太阳光线与DF始终垂直
素 材 2 某地区某天下午不同时间的太阳高度角α(太阳光线与地面的夹角)参照表如下: 时刻12点13点14点15点16点17点太阳高度角α90°75°60°45°30°15°
素 材 3 小明坐在露营椅上的高度(头顶到地面的距离)约为1米.小明坐的位置记为点Q,如图2. 参考数据:≈1.7,≈1.4
问题解决
任 务 1 确定影子长度 某一时刻测得BD=1.7米,请求出此时影子GH的长度
任 务 2 判断是否照射到 这天14点,小明坐在离支架3米处的Q点,请判断此时小明是否被太阳光照射到
续表
任 务 3 探究合理范围 小明打算在这天14:00-15:00露营休息,为保证小明全程不被太阳光照射到,请计算BQ的取值范围
答案全解全析
1.B A.是从上向下看得到的图形,为俯视图,故选项A不合题意;
B.是从左向右看得到的图形,为左视图,故选项B符合题意;
C.不是该实物的视图,故选项C不合题意;
D.是从前往后看得到的图形,是主视图,故选项D不合题意.故选B.
2.C A.主视图是等腰三角形,故此选项不合题意;B.主视图是梯形,故此选项不合题意;C.主视图是圆,故此选项符合题意;D.主视图是矩形,故此选项不合题意.故选C.
3.B 主视图是直角三角形,故A,C,D选项不合题意,故选B.
4.B 由俯视图可得主视图有2列,左边一列有2个小正方形,右边一列有1个小正方形.故选B.
5.C 主视图和左视图相同,都是由上下两个等腰三角形组成的,不是中心对称图形,是轴对称图形.俯视图是圆(带圆心),既是中心对称图形,又是轴对称图形,故选C.
6.C 根据正方体的平面展开图的特征,可知A、B选项折叠后“数”字所在面和“好”字所在面是相对面,不符合题意;D选项折叠后“数”在上面,“好”在右面时,“学”却在背面,与题干图不一致,不符合题意.故选C.
7.B 由题意画出草图,如图,平台上至少还需再放这样的正方体2个,故选B.
8.B ∵AB为底面圆的直径,AB=4,
∴底面圆周长为4π,
圆锥的侧面展开图如图所示,连接AB,
设圆锥的侧面展开后扇形的圆心角为n,
∴4π=,解得n=120°,∴∠ASC=60°,
∵SA=SB,∴△SAB是等边三角形,∵C为SB的中点,∴AC⊥SB.在Rt△ACS中,AC=SA·sin 60°=6×=3,∴蚂蚁爬行的最短路程为3,故选B.
9.15
解析 设投影中对应边的长为x cm,∵三角板与其投影相似,∴对应边之比等于相似比,∴9∶x=3∶5,解得x=15.故答案是15.
10. ①
解析 根据正方体展开图的特征,可知②③④位置都是可以的,只有①不可以,故答案为①.
11.4 m
解析 ∵AB∥CD,∴△ABE∽△CDE,∵相似三角形对应边之比等于对应高之比,∴=.
∵AB=1.2,∴CD=2.又∵FC=2,∴DF=CD+FC=2+2=4(m).故答案为4 m.
12.4
解析 圆心角为120°、半径为6的扇形弧长==4π,
设圆锥底面圆的半径为r,则2πr=4π,解得r=2.
如图,圆锥高OD,底面圆半径DC,与母线OC构成直角三角形,由勾股定理得OD===4,故这个圆锥的高是4.
13.
解析 根据三视图可知这个几何体是圆锥,
圆锥的高为=4,
∴V=π××4=,故答案为.
14.6
解析 根据主视图和俯视图可得该几何体第一层(最底层)有4个小立方块,第二层最多有2个小立方块,∴搭成这个几何体的小立方块最多有4+2=6个,故答案为6.
15.46
解析 这个几何体的主视图有三列,从左到右分别有3,4,1个小正方形,左视图有三列,从左到右分别有3,4,2个小正方形,俯视图有6个小正方形,故几何体表面积为(8+9+6)×2×12=46,故答案为46.
16.(1)3 (2)12
解析 (1)正方体的表面展开图,相对的面之间一定相隔一个正方形,“-3”所在面与“2x-3”所在面是相对面,“y”所在面与“x”所在面是相对面.
∵相对面上的数字或代数式的值互为相反数,
∴2x-3+(-3)=0,x+y=0,解得x=3,y=-3,
故答案是3.
(2)当x=3,y=-3时,x2-y=32-(-3)=12,
故答案是12.
17. 10;(10+)
解析 如图,过点O作AC,BD的平行线,交CD于H,过点O作OJ∥MH交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO到点K,使得OK=OB.
由题意可知点O是AB的中点,∠BJI=∠EGF,
∴△BIJ∽△EFG.
∵OH∥AC∥BD,AO=BO,
∴点H是CD的中点,
∵CD=13 m,∴CH=HD=CD=6.5 m,
∴MH=MC+CH=8.5+6.5=15 m,
由题意可知==,∴=,
解得OM=10 m,∴点O,M之间的距离等于10 m.
∵BI⊥OJ,∴∠BIO=∠BIJ=90°,
由题意可知∠OBJ=∠OBI+∠JBI=90°,
又∵∠BOI+∠OBI=90°,
∴∠BOI=∠JBI,
∴△BOI∽△JBI,∴===,
∴BI=IJ,OI=BI=IJ,
∵OJ∥CD,OH∥DJ,
∴四边形OHDJ是平行四边形,
∴OJ=HD=6.5 m,∵OJ=OI+IJ=IJ+IJ=6.5 m,
∴IJ=4.5 m,∴BI=3 m,OI=2 m,
∵在Rt△OBI中,由勾股定理得OB2=OI2+BI2,
∴OB===(m),
∴OB=OK= m,
∴MK=MO+OK=(10+)m,
∴叶片外端离地面的最大高度等于(10+)m.
故答案为10;(10+).
18.解析 (1)如图所示(下图中的任意两个均可):
(2)∵俯视图有5个正方形,
∴最底层有5个正方体.
由主视图可得第2层最少有2个正方体,第3层最少有1个正方体;由主视图可得第2层最多有4个正方体,第3层最多有2个正方体.
∴该几何体最少有5+2+1=8个正方体,最多有5+4+2=11个正方体,∴n的最小值为8,最大值为11.
(3)如图所示(答案不唯一).
19.解析 (1)如图1,
由题意可知AB⊥BC,EF⊥BC,
∴AB∥EF,∴△EFG∽△ABG,
∴=.
由题意可知EF=3米,AB=9米,FG=4米,
∴=,解得BF=8,即标尺与路灯间的水平距离为8米.
(2)如图2,连接AE交CD于点M,过点M作MN⊥BC交BC延长线于点N,过点M作MG⊥AB于点G,交EF于点H,
∵影子长为4米,∴FC+CM=4米,设CM=x米,
∴FC=(4-x)米,∵AB⊥BC,EF⊥BC,∴AB∥EF,
∴△AGM∽△EHM,∴=,∵CM=x米,=,∴CN=x米,MN=x米,∴HF=GB=MN=x米,GM=BN=BC+CN=米,HM=FN=FC+CN=米,∴AG=AB-BG=米,EH=EF-HF=米,
∴=,
∴2x2+9x-35=0,解得x1=-7(不合题意,舍去),
x2=,经检验,x=是分式方程的解且符合题意,
∴FC=4-x=米,∴BF=15.5-=14米,即标尺与路灯间的水平距离为14米.
20.解析 任务1:如图1,过点E作EI⊥AB于点I,过点G作GJ⊥FH于点J,易知∠DGB=∠JHB=∠α.
∵BD=1.7,AB=2.5,∴AD=0.8,
∵AE=DE=0.5,
∴DF=4DE=2,DI=AD=0.4,
在Rt△EID中,EI==0.3,
∴sin∠IDE==.
∵∠FDG=∠DBG=90°,
∴∠IDE+∠BDG=90°,∠BDG+∠DGB=90°,
∴∠IDE=∠DGB=∠JHB=∠α.
易得四边形DGJF为矩形,
∴GJ=DF=2,
在Rt△GJH中,GH===2×=(米).
任务2:解法一:如图2,过点Q作QP⊥BC交HF于点P.由(1)知,∠IDE=∠α=∠DGB.
∵∠α=60°,∴在Rt△IDE中,DI=DE=,
∴AD=2DI=,∴BD=AB-AD=2.
在Rt△DBG中,BG===,
在Rt△GJH中,GH===.
在Rt△PQH中,当PQ=1时,QH===,
∴小明刚好被照射到时离B点的距离为BG+GH-QH=+-=.∵<3,∴小明会被照射到.
解法二:如图2,过点Q作QP⊥BC交FH于点P.与解法一同理得BG=,GH=,
∴QH=BH-BQ=2-3.在Rt△PQH中,PQ=QH·tan∠α=6-3<1,∴小明会被照射到.
任务3:当tan α=45°时,BQ取得最小值,也即为∠α=45°时BG的长度.由(2)的解法同理可求BQ=BG=.
当tan α=60°时,BQ取得最大值,为=.
∴
21世纪教育网(www.21cnjy.com)
