18.2.3 正方形课件
图片预览




文档简介
课件50张PPT。人教版八年级下册
18.2.3 正方形
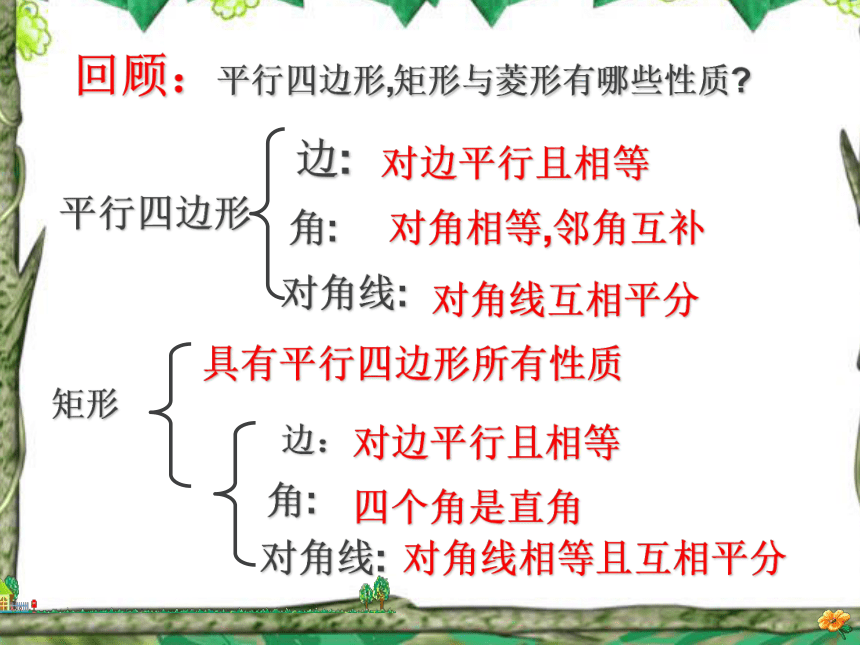
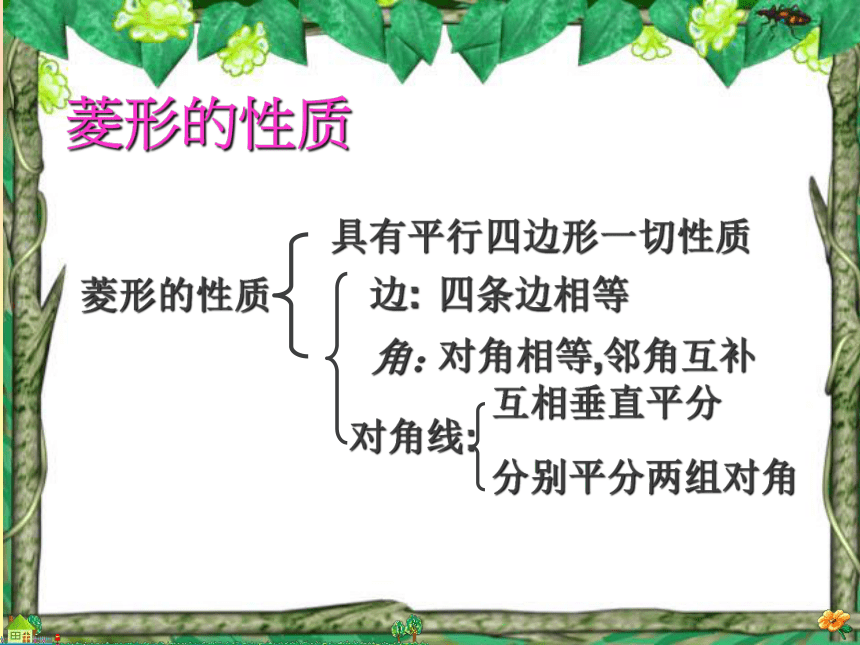
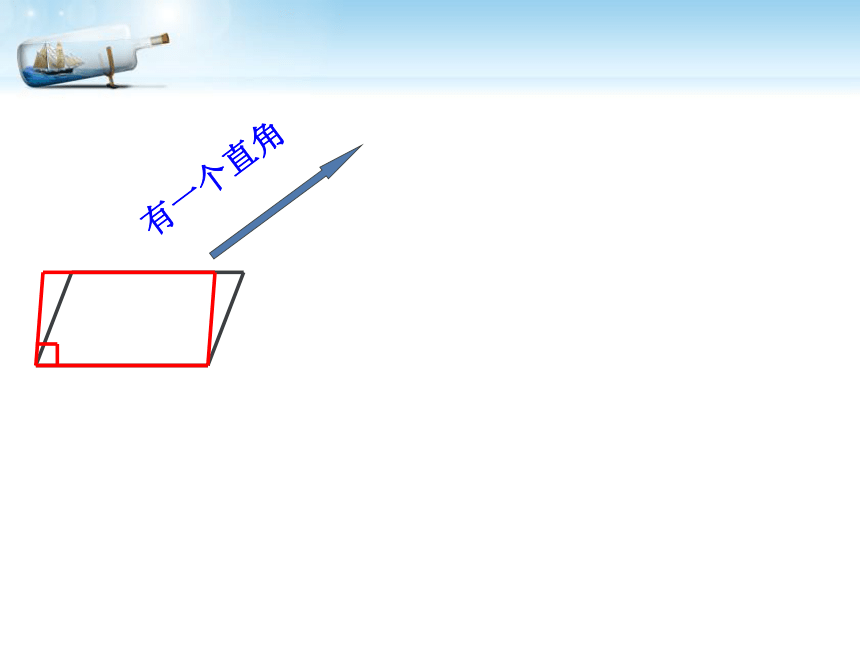
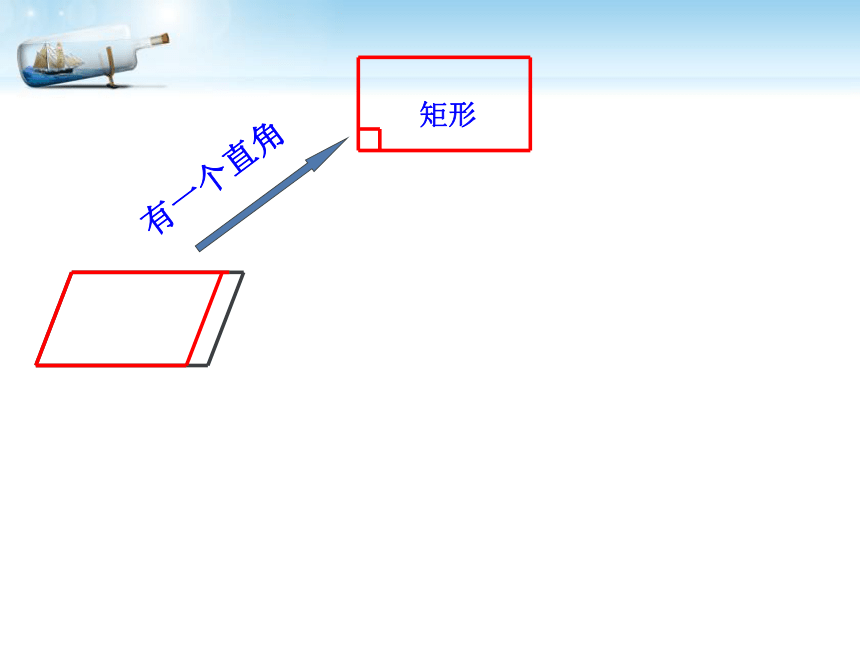
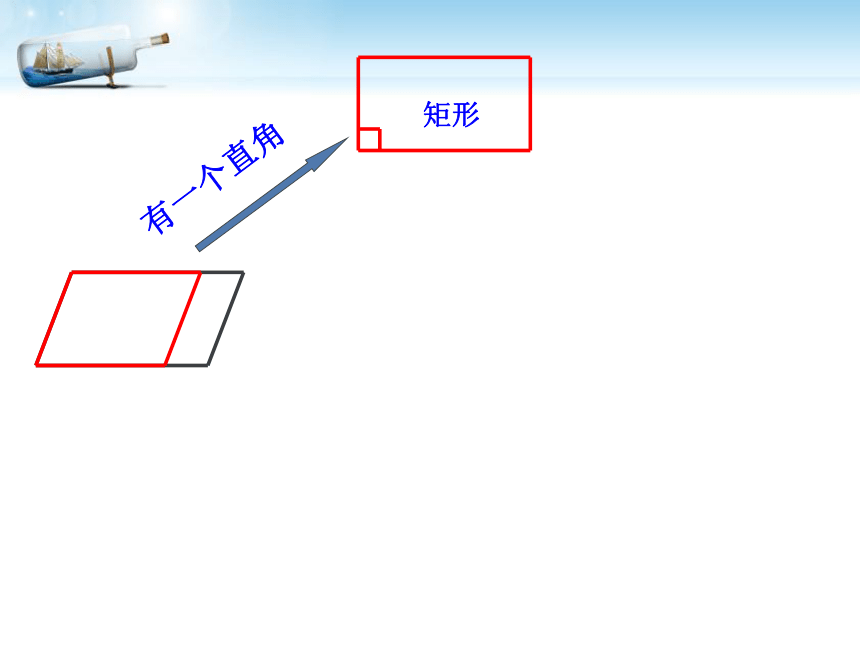
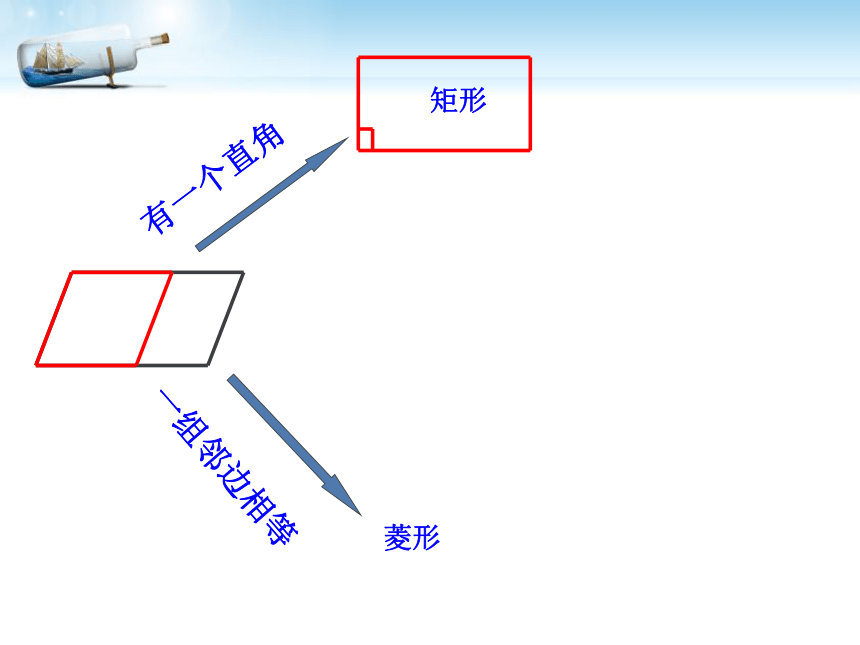
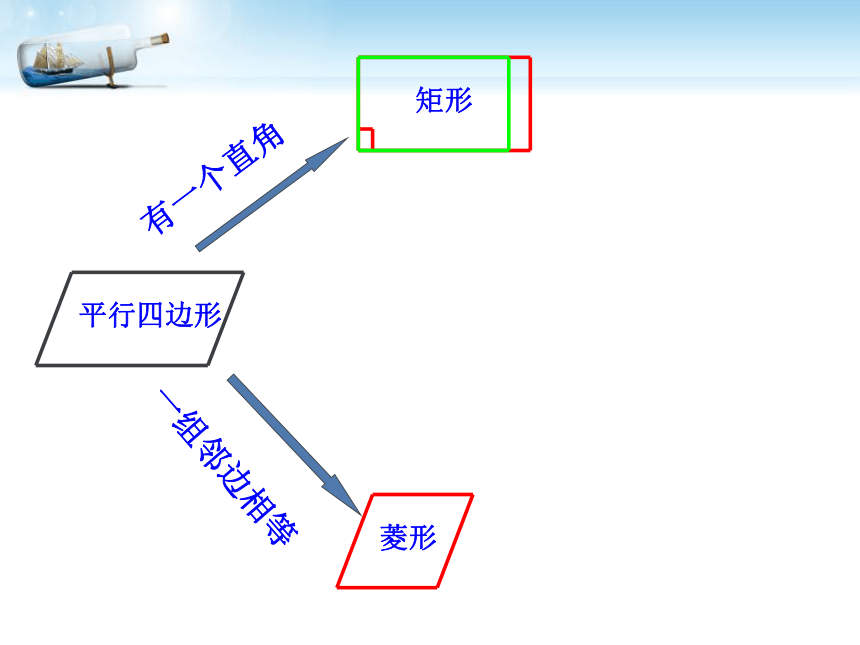
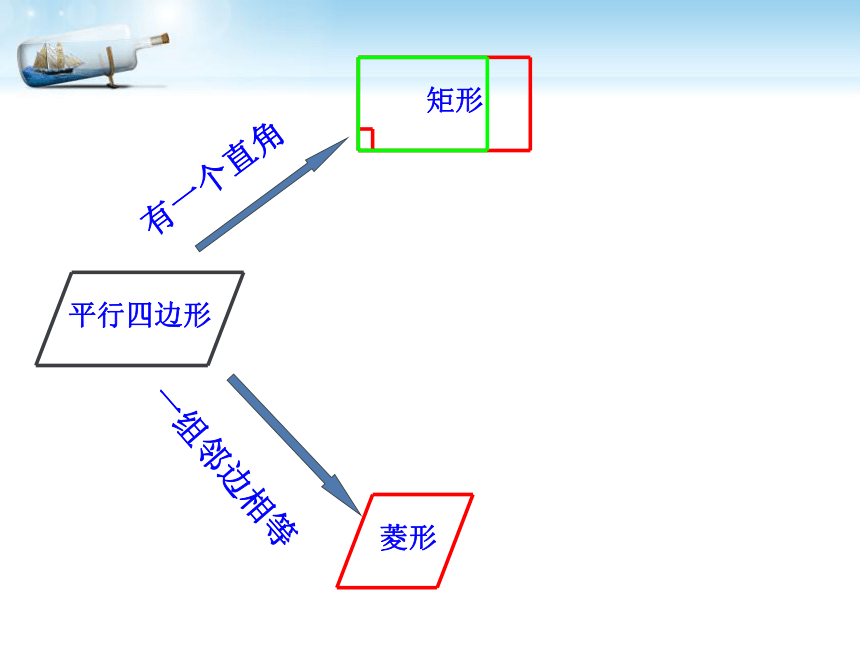
回顾:平行四边形,矩形与菱形有哪些性质?平行四边形边:角:对角线:对边平行且相等对角相等,邻角互补对角线互相平分矩形角:四个角是直角对角线:对角线相等且互相平分边:对边平行且相等具有平行四边形所有性质菱形的性质菱形的性质边:四条边相等对角线:互相垂直平分分别平分两组对角 对角相等,邻角互补具有平行四边形一切性质角:情境一: 观察体会有一个直角有一个直角矩形有一个直角矩形有一个直角一组邻边相等矩形菱形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等有一个直角正方形平行四边形你能给正方形下一个定义吗?问题: 图中CD在平移时,这个图形始终是怎样的图形?当CD移动到C?D?位置,此时AD? =AB,四边形ABCD还是矩形吗?AB 两组互相垂直的平行线围成矩形ABCD矩 形正方形〃〃矩形一组邻边相等时变成怎样的图形呢?探究(一)∟∟∟∟正方形探 究(二)菱形有一个角是直角时变成怎样的图形呢?
探究小结矩 形〃〃正方形邻边相等〃〃发现:
一组邻边相等的矩形 叫正方形一个角是直角正方形∟发现:
一个角为直角的菱形叫正方形如何来给正方形下定义?正方形定义1、有一个角是直角且邻边相等的平行四边形叫做正方形;
2、有一个角是直角的菱形是正方形;
3、有一组邻边相等的矩形是正方形
正方形是特殊的平行四边形,又是特殊的菱形,特殊的矩形,你能猜出它具有怎样的性质?边对角线角 正方形的性质正方形对边平行 四边相等正方形的四个角都是直角正方形的对角线相等,互相垂直平分,每条对角线平分一组对角。正方形是中心对称图形,它也是轴对称图形
正方形是一个完美的图形为什么说正方形是一个完美的图形?正方形是中心对称图形,对称中心为点O它也是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)1.对称性2.特征根据图形所具有的性质,在下表相应的空格中打”√”√√√√√√√√√√√√√√√√体会正方形的完美正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。总结:平行四边形、矩形、菱形、正方形的对称性平行四边形 中心对称图形
(对角线的交点)即是中心对称图形,
又是轴对称图形(两条)即是中心对称图形,
又是轴对称图形(两条)即是中心对称图形,
又是轴对称图形(四条)正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角(1)(2)(3)(4)四边形
平行四边形
矩形
菱形
正方形平行四边形矩形四边形菱形正
方
形平行四边形、矩形、菱形、正方形之间关系正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD判断对错: (1)如果一个菱形的两条对角线相等,那么它一定是正方形. (2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形. (3)两条对角线互相垂直平分且相等的四边形,一定是正方形. (4)四条边相等,且有一个角是直角的四边形是正方形.
zx``x````````k对对对对例题解析例题例1.求证:正方形的两条对角线把
这个正方形分成四个全等的等腰直
角三角形。分析分 析:这是一道几何命题的证明,该怎么做?
你会做吗?第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明
图中共有多少个
等腰直角三角形?八个 :△ABC△BCD △CDA △DAB △AOB △AOD △BOC △COD 求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.例1.已知:如图,四边形ABCD是正
方形,对角线AC、BD相交于点O,证明:∵四边形ABCD是正方形,∴AC=BD,AC⊥BD,AO=BO=CO=DO.∴△ABO、△BCO、△CDO、 例2:如图,顺次连接正方形ABCD各边的中点,得到四边形EFGH.求证:四边形EFGH也是正方形. 已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?证明:∵ 四边形ABCD是正方形
∴ ∠A= ∠ B= ∠ C=∠D=90°,AB=AD=DC=BC(正方形的四条边都相等,四个角都是直角).
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌ △CGF ≌ △DHG.
∴EH=FE=GF=HG.
∴四边形EFGH是菱形。
∵ ∠1=∠3.
又 ∠3+∠2=90°
∴ ∠1+∠2=90°
∴ ∠EFH=90 °
∴ 四边形EFGH是正方形(有一个角是直角的菱形是矩形).
变形例3.如图四边形ABCD和DEFG都是正方形,试说明AE=CG解:因为四边形ABCD是正方形根据正方形的四边相等,得AD=CD又知四边形DEFG也是正方形所以 DE=DG又因为正方形的每个内角为90°所以∠ADE+∠EDC=∠CDG+∠EDC所以∠ADE=∠CDG所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD所以AE=CGABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?AD课本课堂练习P59解:连接AC.
∵ 四边形ABCD是正方形∴ ∠B=90°,AB=BC∵ EC=30m,EB=10m∴ S正方形ABCD=( )2=800(m2)∴ ∴ 3.一正方形对角线长为4,则它的面积为 .81.正方形的两条对角线把正方形分成四个全等的 __________________尝试练习2.一正方形边长为4,则它的面积为 .16等腰直角三角形4.正方形ABCD的面积是9cm2,则AB=________AC=___________3cm5.如图,正方形ABCD中,点E是CD边上一点,连接AE交对角线BD于点F,则图中全等三角形共有( ) A BC DE FCA.1对
B.2对
C.3对
D.4对归纳1 .正方形是中心对称图形,轴对称图形。
2.正方形的四条边都相等。
3.正方形的四个角都相等。
4.正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角。有 一组邻边相等 并且 有一个角是直角
平行四边形 是 正方形的已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.求证:(1)AE=AF;(2)EA⊥AF.课后巩固证明:(1)∵ ABCD是正方形
∴AD=AB,∠ADE=∠ABF=90°
在△ABF与△ADC中
AD=AB
∠ADE=∠ABF=90°
DE=BF
∴ △ABF≌△ADE(SAS)
∴ FA=EA ,∠1=∠3
(2)∵∠2+∠3=90 °
∴∠1+∠2=90 °
∴ EA⊥FA
已知:如图,在正方形ABCD中,点E、F在 BD上,且BF=DE. 求证:四边形AECF是菱形.O 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE. Z```x``xk 证明:在正方形ABDE中, AE=AB,∠EAB=90°, 又在正方形ACFG中, AG=AC,∠GAC=90°, ∴∠EAB=∠GAC=90°. ∴∠EAC=∠GAB, ∴△EAC≌△GAB,
∴EC=GB. ∵∠EAC=∠EAB+∠BAC, ∠GAB=∠GAC+∠BAC,ACBD1.若O点移动至E点时,连接AE、CE,你有那些结论?该怎样证明这些结论?如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF解:连接PC∵PE⊥BC , PF⊥DC而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF 如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
6.如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两
正方形重合部分的
面积是A D
B COPQR大显身手7、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,
猜想AE与CG的位置
关系,并证明你的
猜想。AB D ECG F8、如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.求证:
⑴CE=BG;
⑵EG=2AM.MEDFGBCA 1,将一矩形纸片对折后再对折,如图(1)、(2),然后沿图(3)中的虚线剪下,得到①②两部分,将①展开后得到的平面图形一定是( )A.平行四边形 B.矩形
C.菱形 D.正方形
C备选题:3,① 如图,把一个等腰直角△ABC沿斜边上的高BD(裁剪线)剪一刀,从这个三角形中裁下一部分,与剩下部分拼成一个四边形A′BCD(见示意图A). 猜一猜,四边形A′BCD是 ( )形. 试一试,按上述裁剪方法,请你拼一个与图A形状不同的四边形,并在图B中画出示意图. ②在等腰直角三角形ABC中,请你找出与图A不同的裁剪线,把分割成的两部分拼成一个特殊的四边形,请你在图C中画出你拼得的特殊的四边形的示意图.
18.2.3 正方形
回顾:平行四边形,矩形与菱形有哪些性质?平行四边形边:角:对角线:对边平行且相等对角相等,邻角互补对角线互相平分矩形角:四个角是直角对角线:对角线相等且互相平分边:对边平行且相等具有平行四边形所有性质菱形的性质菱形的性质边:四条边相等对角线:互相垂直平分分别平分两组对角 对角相等,邻角互补具有平行四边形一切性质角:情境一: 观察体会有一个直角有一个直角矩形有一个直角矩形有一个直角一组邻边相等矩形菱形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等平行四边形有一个直角一组邻边相等矩形菱形一组邻边相等有一个直角正方形平行四边形你能给正方形下一个定义吗?问题: 图中CD在平移时,这个图形始终是怎样的图形?当CD移动到C?D?位置,此时AD? =AB,四边形ABCD还是矩形吗?AB 两组互相垂直的平行线围成矩形ABCD矩 形正方形〃〃矩形一组邻边相等时变成怎样的图形呢?探究(一)∟∟∟∟正方形探 究(二)菱形有一个角是直角时变成怎样的图形呢?
探究小结矩 形〃〃正方形邻边相等〃〃发现:
一组邻边相等的矩形 叫正方形一个角是直角正方形∟发现:
一个角为直角的菱形叫正方形如何来给正方形下定义?正方形定义1、有一个角是直角且邻边相等的平行四边形叫做正方形;
2、有一个角是直角的菱形是正方形;
3、有一组邻边相等的矩形是正方形
正方形是特殊的平行四边形,又是特殊的菱形,特殊的矩形,你能猜出它具有怎样的性质?边对角线角 正方形的性质正方形对边平行 四边相等正方形的四个角都是直角正方形的对角线相等,互相垂直平分,每条对角线平分一组对角。正方形是中心对称图形,它也是轴对称图形
正方形是一个完美的图形为什么说正方形是一个完美的图形?正方形是中心对称图形,对称中心为点O它也是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角(A)(B)(C)(D)1.对称性2.特征根据图形所具有的性质,在下表相应的空格中打”√”√√√√√√√√√√√√√√√√体会正方形的完美正方形不但具备一般的平行四边形的性质,而且同时具备矩形和菱形的性质。总结:平行四边形、矩形、菱形、正方形的对称性平行四边形 中心对称图形
(对角线的交点)即是中心对称图形,
又是轴对称图形(两条)即是中心对称图形,
又是轴对称图形(两条)即是中心对称图形,
又是轴对称图形(四条)正方形、矩形、菱形以及平行四边形四者之间的关系:
有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角(1)(2)(3)(4)四边形
平行四边形
矩形
菱形
正方形平行四边形矩形四边形菱形正
方
形平行四边形、矩形、菱形、正方形之间关系正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD判断对错: (1)如果一个菱形的两条对角线相等,那么它一定是正方形. (2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形. (3)两条对角线互相垂直平分且相等的四边形,一定是正方形. (4)四条边相等,且有一个角是直角的四边形是正方形.
zx``x````````k对对对对例题解析例题例1.求证:正方形的两条对角线把
这个正方形分成四个全等的等腰直
角三角形。分析分 析:这是一道几何命题的证明,该怎么做?
你会做吗?第一步:根据题意画出图形
第二步:写出已知
第三步:写出求证
第四步:进行证明
图中共有多少个
等腰直角三角形?八个 :△ABC△BCD △CDA △DAB △AOB △AOD △BOC △COD 求证:△ABO、△BCO、△CDO、
△DAO是全等的等腰直角三角形.△DAO都是等腰直角三角形,并且
△ABO≌△BCO≌△CDO≌△DAO.例1.已知:如图,四边形ABCD是正
方形,对角线AC、BD相交于点O,证明:∵四边形ABCD是正方形,∴AC=BD,AC⊥BD,AO=BO=CO=DO.∴△ABO、△BCO、△CDO、 例2:如图,顺次连接正方形ABCD各边的中点,得到四边形EFGH.求证:四边形EFGH也是正方形. 已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗?为什么?证明:∵ 四边形ABCD是正方形
∴ ∠A= ∠ B= ∠ C=∠D=90°,AB=AD=DC=BC(正方形的四条边都相等,四个角都是直角).
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌ △CGF ≌ △DHG.
∴EH=FE=GF=HG.
∴四边形EFGH是菱形。
∵ ∠1=∠3.
又 ∠3+∠2=90°
∴ ∠1+∠2=90°
∴ ∠EFH=90 °
∴ 四边形EFGH是正方形(有一个角是直角的菱形是矩形).
变形例3.如图四边形ABCD和DEFG都是正方形,试说明AE=CG解:因为四边形ABCD是正方形根据正方形的四边相等,得AD=CD又知四边形DEFG也是正方形所以 DE=DG又因为正方形的每个内角为90°所以∠ADE+∠EDC=∠CDG+∠EDC所以∠ADE=∠CDG所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 90° 得到。⊿AED≌ ⊿CGD所以AE=CGABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?AD课本课堂练习P59解:连接AC.
∵ 四边形ABCD是正方形∴ ∠B=90°,AB=BC∵ EC=30m,EB=10m∴ S正方形ABCD=( )2=800(m2)∴ ∴ 3.一正方形对角线长为4,则它的面积为 .81.正方形的两条对角线把正方形分成四个全等的 __________________尝试练习2.一正方形边长为4,则它的面积为 .16等腰直角三角形4.正方形ABCD的面积是9cm2,则AB=________AC=___________3cm5.如图,正方形ABCD中,点E是CD边上一点,连接AE交对角线BD于点F,则图中全等三角形共有( ) A BC DE FCA.1对
B.2对
C.3对
D.4对归纳1 .正方形是中心对称图形,轴对称图形。
2.正方形的四条边都相等。
3.正方形的四个角都相等。
4.正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角。有 一组邻边相等 并且 有一个角是直角
平行四边形 是 正方形的已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.求证:(1)AE=AF;(2)EA⊥AF.课后巩固证明:(1)∵ ABCD是正方形
∴AD=AB,∠ADE=∠ABF=90°
在△ABF与△ADC中
AD=AB
∠ADE=∠ABF=90°
DE=BF
∴ △ABF≌△ADE(SAS)
∴ FA=EA ,∠1=∠3
(2)∵∠2+∠3=90 °
∴∠1+∠2=90 °
∴ EA⊥FA
已知:如图,在正方形ABCD中,点E、F在 BD上,且BF=DE. 求证:四边形AECF是菱形.O 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE. Z```x``xk 证明:在正方形ABDE中, AE=AB,∠EAB=90°, 又在正方形ACFG中, AG=AC,∠GAC=90°, ∴∠EAB=∠GAC=90°. ∴∠EAC=∠GAB, ∴△EAC≌△GAB,
∴EC=GB. ∵∠EAC=∠EAB+∠BAC, ∠GAB=∠GAC+∠BAC,ACBD1.若O点移动至E点时,连接AE、CE,你有那些结论?该怎样证明这些结论?如图所示,正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F。试说明:AP=EF解:连接PC∵PE⊥BC , PF⊥DC而四边形ABCD是正方形∴∠FCE=90°∴四边形PECF是矩形∴PC=EF又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=EF 如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
6.如图,正方形OPQR的一个顶点O是边长为2的正方形ABCD对角线AC与BD的交点,则两
正方形重合部分的
面积是A D
B COPQR大显身手7、如图,四边形ABCD.DEFG都是正方形,连接AE.CG。
(1)求证:AE=CG
(2)观察图形,
猜想AE与CG的位置
关系,并证明你的
猜想。AB D ECG F8、如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.求证:
⑴CE=BG;
⑵EG=2AM.MEDFGBCA 1,将一矩形纸片对折后再对折,如图(1)、(2),然后沿图(3)中的虚线剪下,得到①②两部分,将①展开后得到的平面图形一定是( )A.平行四边形 B.矩形
C.菱形 D.正方形
C备选题:3,① 如图,把一个等腰直角△ABC沿斜边上的高BD(裁剪线)剪一刀,从这个三角形中裁下一部分,与剩下部分拼成一个四边形A′BCD(见示意图A). 猜一猜,四边形A′BCD是 ( )形. 试一试,按上述裁剪方法,请你拼一个与图A形状不同的四边形,并在图B中画出示意图. ②在等腰直角三角形ABC中,请你找出与图A不同的裁剪线,把分割成的两部分拼成一个特殊的四边形,请你在图C中画出你拼得的特殊的四边形的示意图.
