2024冀教版数学九年级下学期课时练--期末素养综合测试(一)(含解析)
文档属性
| 名称 | 2024冀教版数学九年级下学期课时练--期末素养综合测试(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 800.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:03:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023河北石家庄四十二中一模)如图所示的是某几何体的三视图,该几何体是 ( )
A.长方体 B.三棱锥 C.三棱柱 D.正方体
2.事件:①打雷后会下雨;②掷一枚均匀的硬币,反面朝上;③过十字路口时正好遇到绿灯;④煮熟的鸡蛋能孵出小鸡.以上事件中,随机事件有 ( )
A.1个 B.2个 C.3个 D.4个
3.(2023浙江绍兴中考)在一个不透明的袋子里装有2个红球和5个白球,它们除颜色外都相同,从中任意摸出1个球,则摸出的球为红球的概率是 ( )
A. B. C. D.
4.(2023河北唐山一模)如图所示的几何体由六块相同的小正方体搭成,若移走一块小正方体,几何体的左视图发生了改变,则移走的小正方体是 ( )
A.① B.② C.③ D.④
5.(2023北京通州一模)如图1,一个均匀的转盘被平均分成10份,分别标有1,2,3,4,5,6,7,8,9,10.小凯转动转盘做频率估计概率的试验,当转盘停止转动后,指针指向的数字即为试验转出的数字,图2是小凯记录下的试验结果情况,那么小凯记录的试验是 ( )
A.转动转盘后,出现偶数
B.转动转盘后,出现能被3整除的数
C.转动转盘后,出现比6大的数
D.转动转盘后,出现能被5整除的数
6.如图,太阳光线与地面成60°的角,太阳光照射在地面上的一个皮球上,皮球在地面上的投影长是20,则皮球的直径是 ( )
A.15 B.8 C.10 D.30
7.(2023河北石家庄藁城二模)如图,在边长为6的正六边形ABCDEF中,连接BE,CF,相交于点O,若点M,N分别为OB,OF的中点,则MN的长为 ( )
A.6 B.6 C.8 D.9
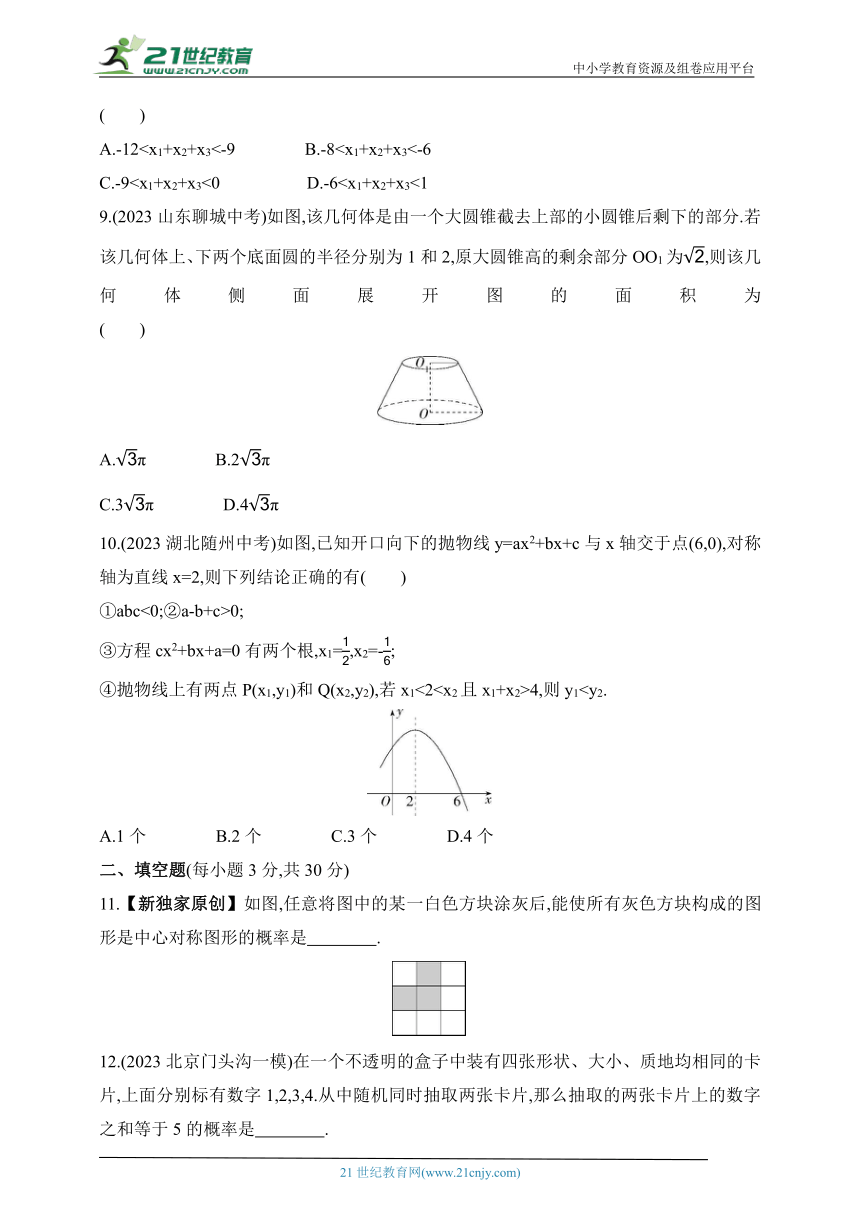
8.(2023湖北十堰中考)已知点A(x1,y1)在直线y=3x+19上,点B(x2,y2),C(x3,y3)在抛物线y=x2+4x-1 上,若y1=y2=y3且x1A.-12C.-99.(2023山东聊城中考)如图,该几何体是由一个大圆锥截去上部的小圆锥后剩下的部分.若该几何体上、下两个底面圆的半径分别为1和2,原大圆锥高的剩余部分OO1为,则该几何体侧面展开图的面积为 ( )
A.π B.2π
C.3π D.4π
10.(2023湖北随州中考)如图,已知开口向下的抛物线y=ax2+bx+c与x轴交于点(6,0),对称轴为直线x=2,则下列结论正确的有( )
①abc<0;②a-b+c>0;
③方程cx2+bx+a=0有两个根,x1=,x2=-;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<24,则y1A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共30分)
11.【新独家原创】如图,任意将图中的某一白色方块涂灰后,能使所有灰色方块构成的图形是中心对称图形的概率是 .
12.(2023北京门头沟一模)在一个不透明的盒子中装有四张形状、大小、质地均相同的卡片,上面分别标有数字1,2,3,4.从中随机同时抽取两张卡片,那么抽取的两张卡片上的数字之和等于5的概率是 .
13.(2023江苏扬州中考)用半径为24 cm,面积为120π cm2的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 cm.
14.将抛物线y=x2-4x-4向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为 .
15.【新独家原创】如图,纸板上有19个无阴影的小正方形,从中选涂1个,使它与图中5个有阴影的小正方形组成一个正方体纸盒的表面展开图,一共有 种选法.
16.不透明的盒子中装有红色、黄色的小球共20个,除颜色外无其他差别,随机摸出一个小球,记下颜色后放回并摇匀,再随机摸出一个球,下图显示了某数学小组开展上述摸球试验的结果.
①当摸球次数是300时,记录“摸到红球”的次数是99,所以“摸到红球”的概率是0.33;
②随着试验次数的增加,“摸到红球”的频率总在0.35附近摆动,显示出一定的稳定性,可以估计“摸到红球”的概率是0.35;
③可以根据本次试验结果,计算出盒子中约有红球7个;
④若再次开展上述摸球试验,则当摸球次数为500时,“摸到红球”的频率一定是0.40.
上面四个推断中正确的是 .
17.(2022贵州黔东南州中考)如图,在△ABC中,∠A=80°,半径为3 cm的☉O是△ABC的内切圆,连接OB、OC,则图中阴影部分的面积是 cm2.(结果用含π的式子表示)
18.请你插上想象的翅膀:图2中六个正方体的侧面展开图有可能是图1的是 .
A B C D E F
图2
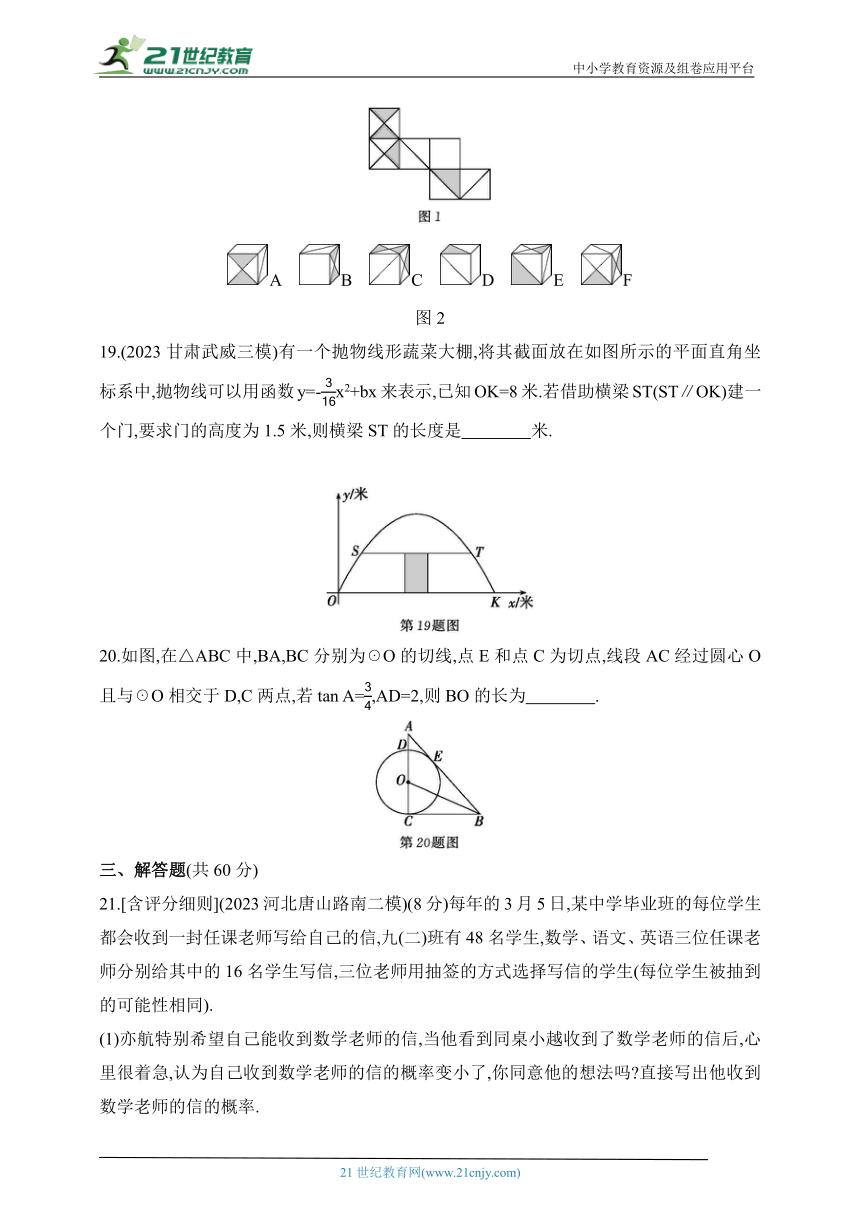
19.(2023甘肃武威三模)有一个抛物线形蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=-x2+bx来表示,已知OK=8米.若借助横梁ST(ST∥OK)建一个门,要求门的高度为1.5米,则横梁ST的长度是 米.
20.如图,在△ABC中,BA,BC分别为☉O的切线,点E和点C为切点,线段AC经过圆心O且与☉O相交于D,C两点,若tan A=,AD=2,则BO的长为 .
三、解答题(共60分)
21.[含评分细则](2023河北唐山路南二模)(8分)每年的3月5日,某中学毕业班的每位学生都会收到一封任课老师写给自己的信,九(二)班有48名学生,数学、语文、英语三位任课老师分别给其中的16名学生写信,三位老师用抽签的方式选择写信的学生(每位学生被抽到的可能性相同).
(1)亦航特别希望自己能收到数学老师的信,当他看到同桌小越收到了数学老师的信后,心里很着急,认为自己收到数学老师的信的概率变小了,你同意他的想法吗 直接写出他收到数学老师的信的概率.
(2)若嘉嘉和淇淇都收到了老师的来信,求她们收到的信来自同一位老师的概率.
22.[含评分细则](2022浙江宁波中考)(10分)为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量y千克与每平方米种植的株数x(2≤x≤8,且x为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克.以同样的栽培条件,每平方米种植的株数每增加1株,平均单株产量减少0.5千克.
(1)求y关于x的函数表达式;
(2)每平方米种植多少株时,能获得最大的产量 最大产量为多少千克
23.[含评分细则](2023河北石家庄十八县联考)(10分)如图所示,在Rt△ABC中,∠C=90°,AB=6,在AB上取点O,以O为圆心,以OB的长为半径作圆,与AC相切于点D,并分别与AB,BC相交于点E,F(异于点B).
(1)求证:BD平分∠ABC;
(2)若点E恰好是AO的中点,求扇形BOF的面积;
(3)若CF的长为1,求☉O的半径.
24.[含评分细则]【新素材】(2023湖北武汉中考)(10分)某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离x(单位:m)、飞行高度y(单位:m)随飞行时间t(单位:s)变化的数据如下表.
飞行时间t/s 0 2 4 6 8 …
飞行水平距离x/m 0 10 20 30 40 …
飞行高度y/m 0 22 40 54 64 …
探究发现 x与t,y与t之间的数量关系可以用我们已学过的函数来描述.直接写出x关于t的函数解析式和y关于t的函数解析式(不要求写出自变量的取值范围).
问题解决 如图,活动小组在水平安全线上A处设置一个高度可以变化的发射平台试飞该航模飞机.根据上面的探究发现解决下列问题.
(1)若发射平台相对于安全线的高度为0 m,求飞机落到安全线上时,飞行的水平距离;
(2)在安全线上设置回收区域MN,AM=125 m,MN=5 m.若飞机落到MN内(不包括端点M,N),求发射平台相对于安全线的高度的变化范围.
25.[含评分细则](2023山东烟台中考)(10分)如图,在菱形ABCD中,对角线AC,BD相交于点E,☉O经过A,D两点,交对角线AC于点F,连接OF交AD于点G,且AG=GD.
(1)求证:AB是☉O的切线;
(2)已知☉O的半径与菱形的边长之比为5∶8,求tan∠ADB的值.
26.[含评分细则](2023湖北武汉中考)(12分)抛物线C1:y=x2-2x-8交x轴于A,B两点(A在B的左边),交y轴于点C.
(1)直接写出A,B,C三点的坐标.
(2)如图1,作直线x=t(0(3)如图2,将抛物线C1平移得到抛物线C2,其顶点为原点,直线y=2x与抛物线C2交于O,G两点,过OG的中点H作直线MN(异于直线OG)交抛物线C2于M,N两点,直线MO与直线GN交于点P,问:点P是否在一条定直线上 若是,求该直线的解析式;若不是,请说明理由.
答案全解全析
1.C 由几何体的主视图和左视图是长方形知该几何体是一个柱体,又∵俯视图是一个三角形,∴该几何体是一个三棱柱.故选C.
2.C ①打雷后可能下雨,也可能不下雨,是随机事件;②掷一枚均匀的硬币,可能反面朝上,也可能正面朝上,是随机事件;③过十字路口时有可能遇到绿灯,也有可能遇到红灯或黄灯,是随机事件;④煮熟的鸡蛋不可能孵出小鸡,④是不可能事件.综上,随机事件有3个,故选C.
3.C 从中任意摸出1个球,共有7种等可能的结果,摸到红球的结果有2种,则摸出红球的概率是,故选C.
4.D 当移走的小正方体是①②③时,左视图为,没有发生变化,当移走的小正方体是④时,左视图为,发生了变化,故选D.
5.B 观察题图2知频率逐渐稳定在0.3,所以试验的概率为0.3.
选项A,转动转盘,出现偶数的概率为=0.5,不符合题意;
选项B,转盘上的数字能被3整除的有3,6,9,故出现能被3整除的数的概率为=0.3,符合题意;
选项C,转盘上比6大的数有7,8,9,10,故出现比6大的数的概率为=0.4,不符合题意;
选项D,转盘上能被5整除的数为5和10,故出现能被5整除的数的概率为=0.2,不符合题意.故选B.
6.D 如图所示,AB为☉O的直径,且垂直于太阳光线,
CE=20,过点C作CD⊥BE于点D,易知四边形ABDC是矩形,
∵太阳光线与地面成60°的角,∴∠DEC=60°,
∴DE=CE=10,∴CD=DE=30,∴AB=CD=30,故选D.
7.D 连接BF(图略),∵在正六边形ABCDEF中,∠A=∠ABC=120°,AB=BC=AF=6,∴∠ABF=∠AFB=30°,∴∠CBF=∠ABC-∠ABF=90°.在正六边形ABCDEF中,∠BOC=60°,OB=OC,∴△BOC是等边三角形,∴∠BCF=60°,∴∠BFC=30°,∴CF=2BC=12,∴BF==18.∵点M,N分别为OB,OF的中点,∴MN是△BOF的中位线,
∴MN=BF=9.故选D.
8.A 如图所示,设直线y=3x+19与抛物线y=x2+4x-1对称轴左边的交点为P, 设抛物线顶点坐标为Q,
联立解得或∴P(-5,4).
y=x2+4x-1=(x+2)2-5, 则Q(-2,-5),抛物线的对称轴为直线x=-2,
设m=y1=y2=y3,则点A,B,C在直线y=m上,
∵y1=y2=y3且x1当m=-5 时,x2=x3,对于y=3x+19,当y=-5时,x=-8,∴x1>-8,∴-8∵对称轴为直线x=-2,∴x2+x3=2×(-2)=-4,
∴x1+x2+x3的取值范围是-129.C 根据题意,补图如下:
OC=2,O1B=1,∵OC∥O1B,
∴△BO1A∽△COA,
∴===,∴AO1=O1O=,∴AB=BC==,∴AC=2,
∴侧面展开图的面积为π×2×2-π×1×=3π,故选C.
10.B 由抛物线的开口方向可知 a<0,由抛物线与y 轴的交点可知c>0,由抛物线的对称轴可知-=2>0,
∴b>0,∴abc<0,故①正确;
∵抛物线y=ax2+bx+c与x轴交于点(6,0),对称轴为直线x=2,则抛物线与x轴的另一个交点坐标为(-2,0),∴x=-1时,y>0,∴a-b+c>0,故②正确;
∵抛物线y=ax2+bx+c与x轴交于点(6,0)和(-2,0),∴ax2+bx+c=0的两根为6和-2,∴6+(-2)=4=-,6×(-2)=-12=,则b=-4a,c=-12a,∴-=-,如果方程cx2+bx+a=0的两个根为x1=,x2=-,即结论③成立,则+==-,这与由题干推出的结论相矛盾,故③不正确;
∵x1<2∵x1+x2>4,∴(x2-2)-(2-x1)=x2-2-2+x1=(x1+x2)-4>0,即点P到对称轴的距离小于点Q到对称轴的距离,∴y1>y2,故④不正确.
综上,①②正确,故选B.
11.
解析 如图,当涂灰1或2或3号区域时,所有灰色方块构成的图形是中心对称图形,则P(是中心对称图形)==.
12.
解析 画树形图如下:
共有12种等可能的结果,其中两张卡片上的数字之和等于5的结果有4种,所以两张卡片上的数字之和等于5的概率是=.
13.5
解析 设圆锥的底面圆的半径为r cm,
由题意,得扇形的面积S=πr×24=120π,
解得r=5,故答案为5.
14.y=(x+1)2-3
解析 y=x2-4x-4=(x-2)2-8,
将抛物线y=(x-2)2-8向左平移3个单位,再向上平移5个单位后,所得抛物线的解析式为y=(x-2+3)2-8+5,即y=(x+1)2-3.
15.4
解析 如图所示:共4种.故答案为4.
16.②③
解析 ①当摸球次数是300时,记录“摸到红球”的次数是99,所以“摸到红球”的概率接近0.33,故推断错误;②随着试验次数的增加,“摸到红球”的频率总在0.35附近摆动,显示出一定的稳定性,可以估计“摸到红球”的概率是0.35,故推断正确;③可以根据本次试验结果,计算出盒子中约有红球20×0.35=7(个),故推断正确;④若再次开展上述摸球试验,则当摸球次数为500时,“摸到红球”的频率在0.35附近,故推断错误.所以正确的推断是②③.
17. π
解析 ∵内切圆圆心是三条角平分线的交点,
∴∠ABO=∠CBO,∠ACO=∠BCO.
设∠ABO=∠CBO=a,∠ACO=∠BCO=b.在△ABC中,∠A+2a+2b=180°①,在△BOC中,∠BOC+a+b=180°②,由①②得∠DOE=90°+∠A=90°+×80°=130°,∴阴影部分的面积是=π(cm2).故答案为π.
18. AE
解析 正方体的表面展开图,相对的面之间一定相隔一个正方形,
与是对面,
与是对面,
与是对面,纵观六个正方体,易知A、E符合题意.
19.4
解析 ∵OK=8,∴点K的坐标是(8,0).把(8,0)代入y=-x2+bx得-×64+8b=0,解得b=,
∴y=-x2+x,∵门的高度为1.5米,ST∥OK,
∴点S和点T的纵坐标均为1.5.
当y=1.5时,-x2+x=1.5,解得x1=4+2,x2=4-2,∴S(4-2,1.5),T(4+2,1.5),∴ST=(4+2)-(4-2)=4,
即横梁ST的长度是4米.
20. 3
解析 连接OE,设☉O的半径为3x(x>0),则OE=OD=OC=3x,
在Rt△AOE中,∵tan A=,∴=,∴=,∴AE=4x,∴AO===5x,
∵AD=2,∴AO=OD+AD=3x+2,∴3x+2=5x,∴x=1,∴OA=3x+2=5,OE=OD=OC=3x=3,
∴AC=OA+OC=5+3=8.
在Rt△ABC中,tan A=,∴BC=AC·tan A=8×=6,∴OB===3.
21.解析 (1)不同意他的想法,1分
他收到数学老师的信的概率为=.3分
(2)将数学、语文、英语三位任课老师的信分别记作A、B、C,
画树形图如下:
6分
共有9种等可能的结果,其中嘉嘉和琪琪收到的信来自同一位老师的有3种,所以收到的信来自同一位老师的概率为=.8分
22.解析 (1)∵每平方米种植的株数每增加1株,平均单株产量减少0.5千克,
∴y=4-0.5(x-2)=-0.5x+5(2≤x≤8,且x为整数).4分
(2)设每平方米小番茄产量为w千克,
w=x(-0.5x+5)=-0.5x2+5x=-0.5(x-5)2+12.5.
∴当x=5时,w有最大值,为12.5.
答:每平方米种植5株时,能获得最大的产量,最大产量为12.5千克.10分
23.解析 (1)证明:连接OD,如图1,
∵AC与☉O相切于点D,∴OD⊥AC,∵∠C=90°,∴BC⊥AC,1分
∴OD∥BC,∴∠CBD=∠ODB,2分
∵OD=OB,∴∠OBD=∠ODB,∴∠OBD=∠CBD,∴BD平分∠ABC.3分
(2)连接DE,OD,OF,如图2,
∵AB=6,E是AO的中点,
∴AE=OE=OB=2,4分
在Rt△AOD中,DE=AO=OE,∴DE=OD=OE,
∴△DOE为等边三角形,∴∠DOE=60°,5分
∵OD∥BC,∴∠FBO=∠DOE=60°,∵OF=OB,
∴△FBO为等边三角形,∴∠BOF=60°,6分
∴S扇形BOF==π.7分
图3
(3)连接OD,过点O作OG⊥BC于点G,如图3,
则BG=FG,四边形DOGC为矩形,
∴DO=CG,8分
设☉O的半径为r,则OD=CG=OB=r,OA=AB-OB=6-r,∵CF=1,∴BG=FG=CG-CF=r-1,
∵OD∥BC,∴∠AOD=∠OBG,9分
∵∠ADO=∠OGB=90°,∴△AOD∽△OBG,∴=,即=,解得r=2或,∴☉O的半径为2或.10分
24.解析 探究发现:x与t是一次函数关系,y与t是二次函数关系,
设x=kt,y=ax2+bx,由题意得10=2k,
解得k=5,a=-,b=12,
∴x=5t,y=-t2+12t.3分
问题解决:(1)依题意,得-t2+12t=0.4分
解得t1=0(舍),t2=24,当t=24时,x=5t=120.
答:飞机落到安全线上时,飞行的水平距离为120 m.5分
(2)设发射平台相对于安全线的高度为n m,飞机相对于安全线的飞行高度y'=-t2+12t+n.6分
∵125在y'=-t2+12t+n中,
当t=25,y'=0时,n=12.5;8分
当t=26,y'=0时,n=26.9分
∴12.5答:发射平台相对于安全线的高度的变化范围是大于12.5 m且小于26 m.10分
25.解析 (1)证明:连接OA(图略),
∵AG=GD,∴由垂径定理的推论知OF⊥AD,
∴∠OGA=∠FGA=90°.1分
∵四边形ABCD是菱形,∴∠GAF=∠BAF,
∴∠GAF+∠AFG=90°=∠BAF+∠AFG.2分
∵OA=OF,∴∠OAF=∠OFA,
∴∠OAF+∠BAF=∠OAB=90°,3分
又∵OA是☉O的半径,∴AB是☉O的切线.4分
(2)设AG=GD=4a(a>0),
∵☉O的半径与菱形的边长之比为5∶8,
∴在Rt△OAG中,OA∶AG=5∶4,6分
∴OA=5a,∴OG==3a,7分
∴FG=OF-OG=2a,8分
∵四边形ABCD是菱形,
∴BD⊥AC,即∠DEA=90°=∠FGA,
又∵∠FAG=∠DAE,∴∠ADB=∠AFG,9分
∴tan∠ADB=tan∠AFG===2.10分
26.解析 (1)∵抛物线的解析式为y=x2-2x-8,
∴当y=0时,x2-2x-8=0,解得x1=-2,x2=4,
当x=0时,y=-8,
∴A(-2,0),B(4,0),C(0,-8).2分
(2)∵F是直线x=t与抛物线C1的交点,
∴F(t,t2-2t-8),
①如图,当△BE1D1∽△CE1F1时,
有∠BCF1=∠CBO,∴CF1∥OB.3分
∵C(0,-8),∴t2-2t-8=-8,
解得t=0(舍去)或t=2.4分
②如图,当△BE2D2∽△F2E2C时,
过F2作F2T⊥y轴于点T.
有∠BCF2=∠BD2E2=∠BOC=90°,
∴∠OCB+∠OBC=∠OCB+∠TCF2=90°,
∴∠TCF2=∠OBC,
∴△BCO∽△CF2T,
∴=.5分
∵B(4,0),C(0,-8),∴OB=4,OC=8,
∵F2T=t,CT=-8-(t2-2t-8)=2t-t2,
∴=,
解得t=0(舍去)或t=.6分
综上,符合题意的t的值为2或.
(3)点P在定直线上.∵将抛物线C1平移得到抛物线C2,其顶点为原点,∴C2:y=x2,
联立直线OG与C2的解析式得
解得(舍去),
∴G(2,4),7分
∵H是OG的中点,∴H(1,2),8分
设M(m,m2),N(n,n2),直线MN的解析式为y=k1x+b1,
则n2=nk1+b1,m2=mk1+b1,解得k1=m+n,b1=-mn,
∴直线MN的解析式为y=(m+n)x-mn,9分
∵直线MN经过点H(1,2),∴m+n-mn=2,
∴mn=m+n-2,
同理可求直线GN的解析式为y=(n+2)x-2n,直线MO的解析式为y=mx,
联立,得
解得x=,y==.10分
∵直线OM与NG相交于点P,
∴P.
设点P在直线y=kx+b上,则=k·+b,①
整理得2m+2n-4=2kn+bn-bm+2b=-bm+(2k+b)n+2b,
比较系数得解得11分
∴当k=2,b=-2时,无论m,n为何值,等式①恒成立.∴点P在定直线y=2x-2上.12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023河北石家庄四十二中一模)如图所示的是某几何体的三视图,该几何体是 ( )
A.长方体 B.三棱锥 C.三棱柱 D.正方体
2.事件:①打雷后会下雨;②掷一枚均匀的硬币,反面朝上;③过十字路口时正好遇到绿灯;④煮熟的鸡蛋能孵出小鸡.以上事件中,随机事件有 ( )
A.1个 B.2个 C.3个 D.4个
3.(2023浙江绍兴中考)在一个不透明的袋子里装有2个红球和5个白球,它们除颜色外都相同,从中任意摸出1个球,则摸出的球为红球的概率是 ( )
A. B. C. D.
4.(2023河北唐山一模)如图所示的几何体由六块相同的小正方体搭成,若移走一块小正方体,几何体的左视图发生了改变,则移走的小正方体是 ( )
A.① B.② C.③ D.④
5.(2023北京通州一模)如图1,一个均匀的转盘被平均分成10份,分别标有1,2,3,4,5,6,7,8,9,10.小凯转动转盘做频率估计概率的试验,当转盘停止转动后,指针指向的数字即为试验转出的数字,图2是小凯记录下的试验结果情况,那么小凯记录的试验是 ( )
A.转动转盘后,出现偶数
B.转动转盘后,出现能被3整除的数
C.转动转盘后,出现比6大的数
D.转动转盘后,出现能被5整除的数
6.如图,太阳光线与地面成60°的角,太阳光照射在地面上的一个皮球上,皮球在地面上的投影长是20,则皮球的直径是 ( )
A.15 B.8 C.10 D.30
7.(2023河北石家庄藁城二模)如图,在边长为6的正六边形ABCDEF中,连接BE,CF,相交于点O,若点M,N分别为OB,OF的中点,则MN的长为 ( )
A.6 B.6 C.8 D.9
8.(2023湖北十堰中考)已知点A(x1,y1)在直线y=3x+19上,点B(x2,y2),C(x3,y3)在抛物线y=x2+4x-1 上,若y1=y2=y3且x1
A.π B.2π
C.3π D.4π
10.(2023湖北随州中考)如图,已知开口向下的抛物线y=ax2+bx+c与x轴交于点(6,0),对称轴为直线x=2,则下列结论正确的有( )
①abc<0;②a-b+c>0;
③方程cx2+bx+a=0有两个根,x1=,x2=-;
④抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<2
二、填空题(每小题3分,共30分)
11.【新独家原创】如图,任意将图中的某一白色方块涂灰后,能使所有灰色方块构成的图形是中心对称图形的概率是 .
12.(2023北京门头沟一模)在一个不透明的盒子中装有四张形状、大小、质地均相同的卡片,上面分别标有数字1,2,3,4.从中随机同时抽取两张卡片,那么抽取的两张卡片上的数字之和等于5的概率是 .
13.(2023江苏扬州中考)用半径为24 cm,面积为120π cm2的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为 cm.
14.将抛物线y=x2-4x-4向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为 .
15.【新独家原创】如图,纸板上有19个无阴影的小正方形,从中选涂1个,使它与图中5个有阴影的小正方形组成一个正方体纸盒的表面展开图,一共有 种选法.
16.不透明的盒子中装有红色、黄色的小球共20个,除颜色外无其他差别,随机摸出一个小球,记下颜色后放回并摇匀,再随机摸出一个球,下图显示了某数学小组开展上述摸球试验的结果.
①当摸球次数是300时,记录“摸到红球”的次数是99,所以“摸到红球”的概率是0.33;
②随着试验次数的增加,“摸到红球”的频率总在0.35附近摆动,显示出一定的稳定性,可以估计“摸到红球”的概率是0.35;
③可以根据本次试验结果,计算出盒子中约有红球7个;
④若再次开展上述摸球试验,则当摸球次数为500时,“摸到红球”的频率一定是0.40.
上面四个推断中正确的是 .
17.(2022贵州黔东南州中考)如图,在△ABC中,∠A=80°,半径为3 cm的☉O是△ABC的内切圆,连接OB、OC,则图中阴影部分的面积是 cm2.(结果用含π的式子表示)
18.请你插上想象的翅膀:图2中六个正方体的侧面展开图有可能是图1的是 .
A B C D E F
图2
19.(2023甘肃武威三模)有一个抛物线形蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=-x2+bx来表示,已知OK=8米.若借助横梁ST(ST∥OK)建一个门,要求门的高度为1.5米,则横梁ST的长度是 米.
20.如图,在△ABC中,BA,BC分别为☉O的切线,点E和点C为切点,线段AC经过圆心O且与☉O相交于D,C两点,若tan A=,AD=2,则BO的长为 .
三、解答题(共60分)
21.[含评分细则](2023河北唐山路南二模)(8分)每年的3月5日,某中学毕业班的每位学生都会收到一封任课老师写给自己的信,九(二)班有48名学生,数学、语文、英语三位任课老师分别给其中的16名学生写信,三位老师用抽签的方式选择写信的学生(每位学生被抽到的可能性相同).
(1)亦航特别希望自己能收到数学老师的信,当他看到同桌小越收到了数学老师的信后,心里很着急,认为自己收到数学老师的信的概率变小了,你同意他的想法吗 直接写出他收到数学老师的信的概率.
(2)若嘉嘉和淇淇都收到了老师的来信,求她们收到的信来自同一位老师的概率.
22.[含评分细则](2022浙江宁波中考)(10分)为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量y千克与每平方米种植的株数x(2≤x≤8,且x为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克.以同样的栽培条件,每平方米种植的株数每增加1株,平均单株产量减少0.5千克.
(1)求y关于x的函数表达式;
(2)每平方米种植多少株时,能获得最大的产量 最大产量为多少千克
23.[含评分细则](2023河北石家庄十八县联考)(10分)如图所示,在Rt△ABC中,∠C=90°,AB=6,在AB上取点O,以O为圆心,以OB的长为半径作圆,与AC相切于点D,并分别与AB,BC相交于点E,F(异于点B).
(1)求证:BD平分∠ABC;
(2)若点E恰好是AO的中点,求扇形BOF的面积;
(3)若CF的长为1,求☉O的半径.
24.[含评分细则]【新素材】(2023湖北武汉中考)(10分)某课外科技活动小组研制了一种航模飞机.通过实验,收集了飞机相对于出发点的飞行水平距离x(单位:m)、飞行高度y(单位:m)随飞行时间t(单位:s)变化的数据如下表.
飞行时间t/s 0 2 4 6 8 …
飞行水平距离x/m 0 10 20 30 40 …
飞行高度y/m 0 22 40 54 64 …
探究发现 x与t,y与t之间的数量关系可以用我们已学过的函数来描述.直接写出x关于t的函数解析式和y关于t的函数解析式(不要求写出自变量的取值范围).
问题解决 如图,活动小组在水平安全线上A处设置一个高度可以变化的发射平台试飞该航模飞机.根据上面的探究发现解决下列问题.
(1)若发射平台相对于安全线的高度为0 m,求飞机落到安全线上时,飞行的水平距离;
(2)在安全线上设置回收区域MN,AM=125 m,MN=5 m.若飞机落到MN内(不包括端点M,N),求发射平台相对于安全线的高度的变化范围.
25.[含评分细则](2023山东烟台中考)(10分)如图,在菱形ABCD中,对角线AC,BD相交于点E,☉O经过A,D两点,交对角线AC于点F,连接OF交AD于点G,且AG=GD.
(1)求证:AB是☉O的切线;
(2)已知☉O的半径与菱形的边长之比为5∶8,求tan∠ADB的值.
26.[含评分细则](2023湖北武汉中考)(12分)抛物线C1:y=x2-2x-8交x轴于A,B两点(A在B的左边),交y轴于点C.
(1)直接写出A,B,C三点的坐标.
(2)如图1,作直线x=t(0
答案全解全析
1.C 由几何体的主视图和左视图是长方形知该几何体是一个柱体,又∵俯视图是一个三角形,∴该几何体是一个三棱柱.故选C.
2.C ①打雷后可能下雨,也可能不下雨,是随机事件;②掷一枚均匀的硬币,可能反面朝上,也可能正面朝上,是随机事件;③过十字路口时有可能遇到绿灯,也有可能遇到红灯或黄灯,是随机事件;④煮熟的鸡蛋不可能孵出小鸡,④是不可能事件.综上,随机事件有3个,故选C.
3.C 从中任意摸出1个球,共有7种等可能的结果,摸到红球的结果有2种,则摸出红球的概率是,故选C.
4.D 当移走的小正方体是①②③时,左视图为,没有发生变化,当移走的小正方体是④时,左视图为,发生了变化,故选D.
5.B 观察题图2知频率逐渐稳定在0.3,所以试验的概率为0.3.
选项A,转动转盘,出现偶数的概率为=0.5,不符合题意;
选项B,转盘上的数字能被3整除的有3,6,9,故出现能被3整除的数的概率为=0.3,符合题意;
选项C,转盘上比6大的数有7,8,9,10,故出现比6大的数的概率为=0.4,不符合题意;
选项D,转盘上能被5整除的数为5和10,故出现能被5整除的数的概率为=0.2,不符合题意.故选B.
6.D 如图所示,AB为☉O的直径,且垂直于太阳光线,
CE=20,过点C作CD⊥BE于点D,易知四边形ABDC是矩形,
∵太阳光线与地面成60°的角,∴∠DEC=60°,
∴DE=CE=10,∴CD=DE=30,∴AB=CD=30,故选D.
7.D 连接BF(图略),∵在正六边形ABCDEF中,∠A=∠ABC=120°,AB=BC=AF=6,∴∠ABF=∠AFB=30°,∴∠CBF=∠ABC-∠ABF=90°.在正六边形ABCDEF中,∠BOC=60°,OB=OC,∴△BOC是等边三角形,∴∠BCF=60°,∴∠BFC=30°,∴CF=2BC=12,∴BF==18.∵点M,N分别为OB,OF的中点,∴MN是△BOF的中位线,
∴MN=BF=9.故选D.
8.A 如图所示,设直线y=3x+19与抛物线y=x2+4x-1对称轴左边的交点为P, 设抛物线顶点坐标为Q,
联立解得或∴P(-5,4).
y=x2+4x-1=(x+2)2-5, 则Q(-2,-5),抛物线的对称轴为直线x=-2,
设m=y1=y2=y3,则点A,B,C在直线y=m上,
∵y1=y2=y3且x1
∴x1+x2+x3的取值范围是-12
OC=2,O1B=1,∵OC∥O1B,
∴△BO1A∽△COA,
∴===,∴AO1=O1O=,∴AB=BC==,∴AC=2,
∴侧面展开图的面积为π×2×2-π×1×=3π,故选C.
10.B 由抛物线的开口方向可知 a<0,由抛物线与y 轴的交点可知c>0,由抛物线的对称轴可知-=2>0,
∴b>0,∴abc<0,故①正确;
∵抛物线y=ax2+bx+c与x轴交于点(6,0),对称轴为直线x=2,则抛物线与x轴的另一个交点坐标为(-2,0),∴x=-1时,y>0,∴a-b+c>0,故②正确;
∵抛物线y=ax2+bx+c与x轴交于点(6,0)和(-2,0),∴ax2+bx+c=0的两根为6和-2,∴6+(-2)=4=-,6×(-2)=-12=,则b=-4a,c=-12a,∴-=-,如果方程cx2+bx+a=0的两个根为x1=,x2=-,即结论③成立,则+==-,这与由题干推出的结论相矛盾,故③不正确;
∵x1<2
综上,①②正确,故选B.
11.
解析 如图,当涂灰1或2或3号区域时,所有灰色方块构成的图形是中心对称图形,则P(是中心对称图形)==.
12.
解析 画树形图如下:
共有12种等可能的结果,其中两张卡片上的数字之和等于5的结果有4种,所以两张卡片上的数字之和等于5的概率是=.
13.5
解析 设圆锥的底面圆的半径为r cm,
由题意,得扇形的面积S=πr×24=120π,
解得r=5,故答案为5.
14.y=(x+1)2-3
解析 y=x2-4x-4=(x-2)2-8,
将抛物线y=(x-2)2-8向左平移3个单位,再向上平移5个单位后,所得抛物线的解析式为y=(x-2+3)2-8+5,即y=(x+1)2-3.
15.4
解析 如图所示:共4种.故答案为4.
16.②③
解析 ①当摸球次数是300时,记录“摸到红球”的次数是99,所以“摸到红球”的概率接近0.33,故推断错误;②随着试验次数的增加,“摸到红球”的频率总在0.35附近摆动,显示出一定的稳定性,可以估计“摸到红球”的概率是0.35,故推断正确;③可以根据本次试验结果,计算出盒子中约有红球20×0.35=7(个),故推断正确;④若再次开展上述摸球试验,则当摸球次数为500时,“摸到红球”的频率在0.35附近,故推断错误.所以正确的推断是②③.
17. π
解析 ∵内切圆圆心是三条角平分线的交点,
∴∠ABO=∠CBO,∠ACO=∠BCO.
设∠ABO=∠CBO=a,∠ACO=∠BCO=b.在△ABC中,∠A+2a+2b=180°①,在△BOC中,∠BOC+a+b=180°②,由①②得∠DOE=90°+∠A=90°+×80°=130°,∴阴影部分的面积是=π(cm2).故答案为π.
18. AE
解析 正方体的表面展开图,相对的面之间一定相隔一个正方形,
与是对面,
与是对面,
与是对面,纵观六个正方体,易知A、E符合题意.
19.4
解析 ∵OK=8,∴点K的坐标是(8,0).把(8,0)代入y=-x2+bx得-×64+8b=0,解得b=,
∴y=-x2+x,∵门的高度为1.5米,ST∥OK,
∴点S和点T的纵坐标均为1.5.
当y=1.5时,-x2+x=1.5,解得x1=4+2,x2=4-2,∴S(4-2,1.5),T(4+2,1.5),∴ST=(4+2)-(4-2)=4,
即横梁ST的长度是4米.
20. 3
解析 连接OE,设☉O的半径为3x(x>0),则OE=OD=OC=3x,
在Rt△AOE中,∵tan A=,∴=,∴=,∴AE=4x,∴AO===5x,
∵AD=2,∴AO=OD+AD=3x+2,∴3x+2=5x,∴x=1,∴OA=3x+2=5,OE=OD=OC=3x=3,
∴AC=OA+OC=5+3=8.
在Rt△ABC中,tan A=,∴BC=AC·tan A=8×=6,∴OB===3.
21.解析 (1)不同意他的想法,1分
他收到数学老师的信的概率为=.3分
(2)将数学、语文、英语三位任课老师的信分别记作A、B、C,
画树形图如下:
6分
共有9种等可能的结果,其中嘉嘉和琪琪收到的信来自同一位老师的有3种,所以收到的信来自同一位老师的概率为=.8分
22.解析 (1)∵每平方米种植的株数每增加1株,平均单株产量减少0.5千克,
∴y=4-0.5(x-2)=-0.5x+5(2≤x≤8,且x为整数).4分
(2)设每平方米小番茄产量为w千克,
w=x(-0.5x+5)=-0.5x2+5x=-0.5(x-5)2+12.5.
∴当x=5时,w有最大值,为12.5.
答:每平方米种植5株时,能获得最大的产量,最大产量为12.5千克.10分
23.解析 (1)证明:连接OD,如图1,
∵AC与☉O相切于点D,∴OD⊥AC,∵∠C=90°,∴BC⊥AC,1分
∴OD∥BC,∴∠CBD=∠ODB,2分
∵OD=OB,∴∠OBD=∠ODB,∴∠OBD=∠CBD,∴BD平分∠ABC.3分
(2)连接DE,OD,OF,如图2,
∵AB=6,E是AO的中点,
∴AE=OE=OB=2,4分
在Rt△AOD中,DE=AO=OE,∴DE=OD=OE,
∴△DOE为等边三角形,∴∠DOE=60°,5分
∵OD∥BC,∴∠FBO=∠DOE=60°,∵OF=OB,
∴△FBO为等边三角形,∴∠BOF=60°,6分
∴S扇形BOF==π.7分
图3
(3)连接OD,过点O作OG⊥BC于点G,如图3,
则BG=FG,四边形DOGC为矩形,
∴DO=CG,8分
设☉O的半径为r,则OD=CG=OB=r,OA=AB-OB=6-r,∵CF=1,∴BG=FG=CG-CF=r-1,
∵OD∥BC,∴∠AOD=∠OBG,9分
∵∠ADO=∠OGB=90°,∴△AOD∽△OBG,∴=,即=,解得r=2或,∴☉O的半径为2或.10分
24.解析 探究发现:x与t是一次函数关系,y与t是二次函数关系,
设x=kt,y=ax2+bx,由题意得10=2k,
解得k=5,a=-,b=12,
∴x=5t,y=-t2+12t.3分
问题解决:(1)依题意,得-t2+12t=0.4分
解得t1=0(舍),t2=24,当t=24时,x=5t=120.
答:飞机落到安全线上时,飞行的水平距离为120 m.5分
(2)设发射平台相对于安全线的高度为n m,飞机相对于安全线的飞行高度y'=-t2+12t+n.6分
∵125
当t=25,y'=0时,n=12.5;8分
当t=26,y'=0时,n=26.9分
∴12.5
25.解析 (1)证明:连接OA(图略),
∵AG=GD,∴由垂径定理的推论知OF⊥AD,
∴∠OGA=∠FGA=90°.1分
∵四边形ABCD是菱形,∴∠GAF=∠BAF,
∴∠GAF+∠AFG=90°=∠BAF+∠AFG.2分
∵OA=OF,∴∠OAF=∠OFA,
∴∠OAF+∠BAF=∠OAB=90°,3分
又∵OA是☉O的半径,∴AB是☉O的切线.4分
(2)设AG=GD=4a(a>0),
∵☉O的半径与菱形的边长之比为5∶8,
∴在Rt△OAG中,OA∶AG=5∶4,6分
∴OA=5a,∴OG==3a,7分
∴FG=OF-OG=2a,8分
∵四边形ABCD是菱形,
∴BD⊥AC,即∠DEA=90°=∠FGA,
又∵∠FAG=∠DAE,∴∠ADB=∠AFG,9分
∴tan∠ADB=tan∠AFG===2.10分
26.解析 (1)∵抛物线的解析式为y=x2-2x-8,
∴当y=0时,x2-2x-8=0,解得x1=-2,x2=4,
当x=0时,y=-8,
∴A(-2,0),B(4,0),C(0,-8).2分
(2)∵F是直线x=t与抛物线C1的交点,
∴F(t,t2-2t-8),
①如图,当△BE1D1∽△CE1F1时,
有∠BCF1=∠CBO,∴CF1∥OB.3分
∵C(0,-8),∴t2-2t-8=-8,
解得t=0(舍去)或t=2.4分
②如图,当△BE2D2∽△F2E2C时,
过F2作F2T⊥y轴于点T.
有∠BCF2=∠BD2E2=∠BOC=90°,
∴∠OCB+∠OBC=∠OCB+∠TCF2=90°,
∴∠TCF2=∠OBC,
∴△BCO∽△CF2T,
∴=.5分
∵B(4,0),C(0,-8),∴OB=4,OC=8,
∵F2T=t,CT=-8-(t2-2t-8)=2t-t2,
∴=,
解得t=0(舍去)或t=.6分
综上,符合题意的t的值为2或.
(3)点P在定直线上.∵将抛物线C1平移得到抛物线C2,其顶点为原点,∴C2:y=x2,
联立直线OG与C2的解析式得
解得(舍去),
∴G(2,4),7分
∵H是OG的中点,∴H(1,2),8分
设M(m,m2),N(n,n2),直线MN的解析式为y=k1x+b1,
则n2=nk1+b1,m2=mk1+b1,解得k1=m+n,b1=-mn,
∴直线MN的解析式为y=(m+n)x-mn,9分
∵直线MN经过点H(1,2),∴m+n-mn=2,
∴mn=m+n-2,
同理可求直线GN的解析式为y=(n+2)x-2n,直线MO的解析式为y=mx,
联立,得
解得x=,y==.10分
∵直线OM与NG相交于点P,
∴P.
设点P在直线y=kx+b上,则=k·+b,①
整理得2m+2n-4=2kn+bn-bm+2b=-bm+(2k+b)n+2b,
比较系数得解得11分
∴当k=2,b=-2时,无论m,n为何值,等式①恒成立.∴点P在定直线y=2x-2上.12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
