29.3.2 切线的判定课时练(含解析)
文档属性
| 名称 | 29.3.2 切线的判定课时练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 449.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:08:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
第二十九章 直线与圆的位置关系
29.3 切线的性质和判定
29.3.2 切线的判定
基础过关全练
知识点 圆的切线的判定
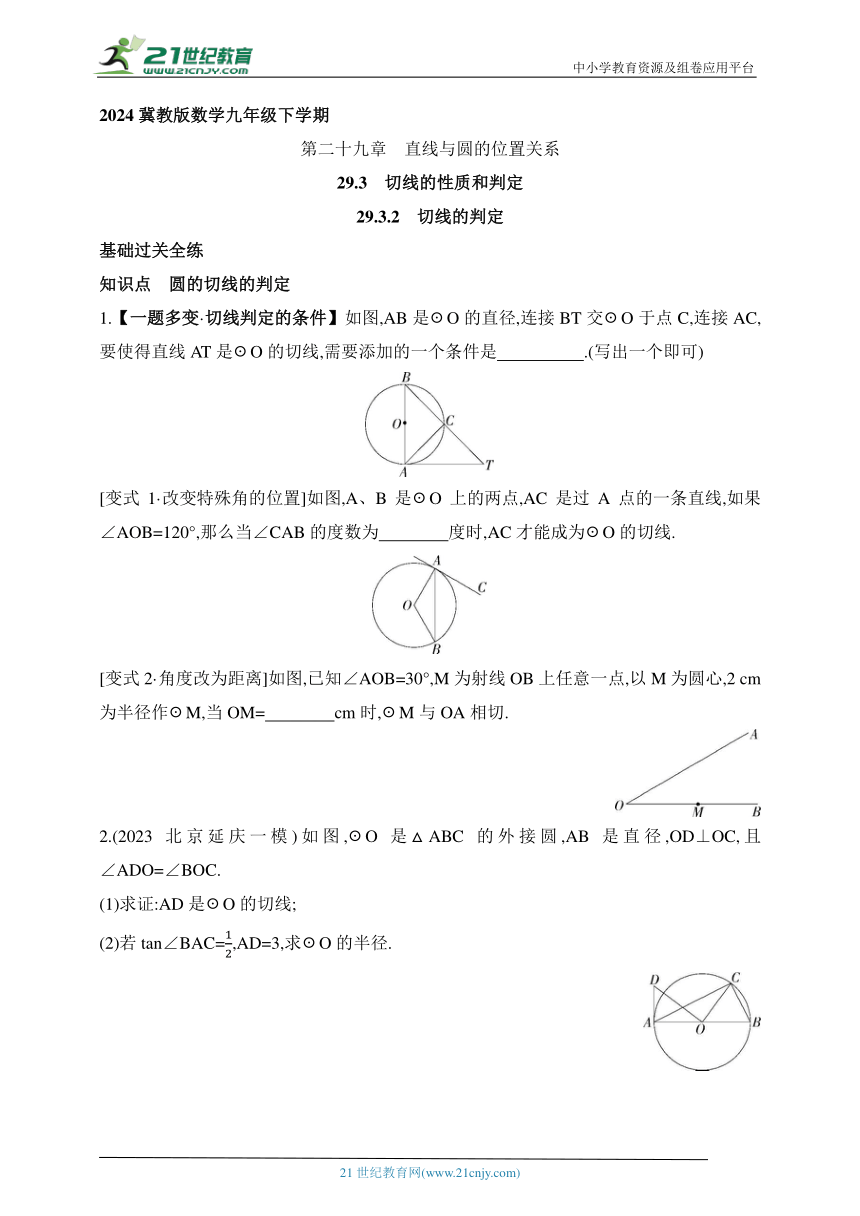
1.【一题多变·切线判定的条件】如图,AB是☉O的直径,连接BT交☉O于点C,连接AC,要使得直线AT是☉O的切线,需要添加的一个条件是 .(写出一个即可)
[变式1·改变特殊角的位置]如图,A、B是☉O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数为 度时,AC才能成为☉O的切线.
[变式2·角度改为距离]如图,已知∠AOB=30°,M为射线OB上任意一点,以M为圆心,2 cm为半径作☉M,当OM= cm时,☉M与OA相切.
2.(2023北京延庆一模)如图,☉O是△ABC的外接圆,AB是直径,OD⊥OC,且∠ADO=∠BOC.
(1)求证:AD是☉O的切线;
(2)若tan∠BAC=,AD=3,求☉O的半径.
能力提升全练
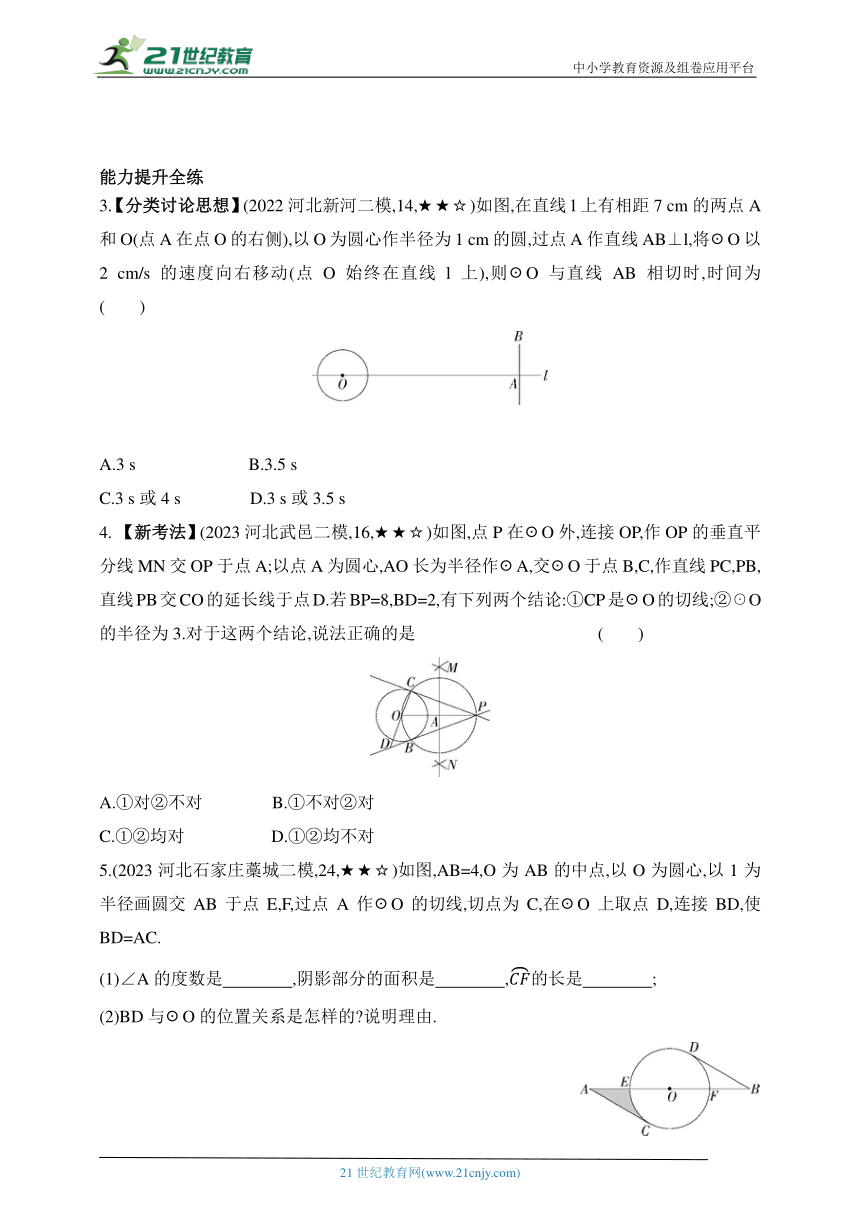
3.【分类讨论思想】(2022河北新河二模,14,★★☆)如图,在直线l上有相距7 cm的两点A和O(点A在点O的右侧),以O为圆心作半径为1 cm的圆,过点A作直线AB⊥l,将☉O以2 cm/s的速度向右移动(点O始终在直线l上),则☉O与直线AB相切时,时间为 ( )
A.3 s B.3.5 s
C.3 s或4 s D.3 s或3.5 s
4. 【新考法】(2023河北武邑二模,16,★★☆)如图,点P在☉O外,连接OP,作OP的垂直平分线MN交OP于点A;以点A为圆心,AO长为半径作☉A,交☉O于点B,C,作直线PC,PB,直线PB交CO的延长线于点D.若BP=8,BD=2,有下列两个结论:①CP是☉O的切线;②☉O的半径为3.对于这两个结论,说法正确的是 ( )
A.①对②不对 B.①不对②对
C.①②均对 D.①②均不对
5.(2023河北石家庄藁城二模,24,★★☆)如图,AB=4,O为AB的中点,以O为圆心,以1为半径画圆交AB于点E,F,过点A作☉O的切线,切点为C,在☉O上取点D,连接BD,使BD=AC.
(1)∠A的度数是 ,阴影部分的面积是 ,的长是 ;
(2)BD与☉O的位置关系是怎样的 说明理由.
6.(2023湖南永州中考,25,★★☆)如图,以AB为直径的☉O是△ABC的外接圆,延长BC到点D,使得∠BAC=∠BDA,点E在DA的延长线上,点M在线段AC上,CE交BM于N,CE交AB于G.
(1)求证:ED是☉O的切线;
(2)若AC=,BD=5,AC>CD,求BC的长;
(3)若DE·AM=AC·AD,求证:BM⊥CE.
素养探究全练
7.【几何直观】(2023四川遂宁中考)如图,四边形ABCD内接于☉O,AB为☉O的直径,AD=CD,过点D的直线l交BA的延长线于点M,交BC的延长线于点N,且∠ADM=∠DAC.
(1)求证:MN是☉O的切线;
(2)求证:AD2=AB·CN;
(3)当AB=6,sin∠DCA=时,求AM的长.
答案全解全析
基础过关全练
1.∠ABT=∠ATB=45°(答案不唯一)
解析 添加条件:∠ABT=∠ATB=45°,
∵∠ABT=∠ATB=45°,∴∠BAT=90°,
又∵AB是圆O的直径,∴AT是圆O的切线,
故答案为∠ABT=∠ATB=45°(答案不唯一).
[变式1] 60
解析 ∵△AOB中,OA=OB,∠AOB=120°,
∴∠OAB=∠OBA=(180°-∠AOB)=30°,
∵当OA⊥AC,即∠OAC=90°时,AC才能成为☉O的切线,∴当∠CAB的度数为60°时,AC才能成为☉O的切线.故答案为60.
[变式2] 4
解析 当☉M与直线OA相切时,过M作MN⊥OA于点N,N为切点,∵∠AOB=30°,∠ONM=90°,∴OM=2MN=4 cm,则当OM=4 cm时,☉M与OA相切.
2.解析 (1)证明:∵OD⊥OC,∴∠DOC=90°,
∴∠AOD+∠BOC=90°.∵∠ADO=∠BOC,
∴∠AOD+∠ADO=90°,∴∠DAO=90°.
∵AB是☉O的直径,∴AD是☉O的切线.
(2)∵AB是☉O的直径,∴∠ACB=90°,∴∠BAC+∠B=90°.过点C作CE⊥AB于点E,∴∠ECB+∠B=90°,∴∠BAC=∠ECB.
∵tan∠BAC=,∴tan∠ECB=.
设BE=a(a>0),则CE=2a,BC=a,
∴AC=2a,AB=5a,∴OA=OB=a,∴OE=a.
∵∠DAO=∠OEC=90°,∠ADO=∠BOC,
∴△ADO∽△EOC,∴=,∴==.
∵AD=3,∴OA=4,即☉O的半径为4.
能力提升全练
3.C 当点O到AB的距离为1 cm时,☉O与AB相切,
∵开始时O点到AB的距离为7 cm,
∴当圆向右移动(7-1)cm或(7+1)cm时,点O到AB的距离为1 cm,此时☉O与AB相切,
∴t==3(s)或t==4(s),即☉O与直线AB在☉O运动3 s或4 s时相切,故选C.
4.A 本题结合尺规作图考查切线的判定.
①∵MN垂直平分OP,交OP于点A,
又以点A为圆心,AO长为半径作☉A,
∴点P在☉A上,OP为☉A的直径,
∴∠PCO=90°,∵OC是☉O的半径,
∴CP是☉O的切线,故①对.
②连接OB,如图,设OB=r,
∵OP为☉A的直径,∴∠PBO=90°,在Rt△PBO和Rt△PCO中,
∴△PBO≌△PCO(HL),
∴PB=PC=8.在△DBO和△DCP中,∠ODB=∠PDC,∠DBO=∠DCP=90°,
∴△DBO∽△DCP,
∴=,即=,∴OD=r.
在Rt△OBD中,OD2=DB2+OB2,
∴=22+r2,解得r=(舍负),故②错误.
故选A.
5.解析 (1)如图,连接OC,
∵AB=4,O为AB的中点,∴AO=BO=2,
∵AC与☉O相切,∴∠ACO=90°,又∵OC=1,
∴sin A==,AC==,
∴∠A=30°,∴∠AOC=60°,
∴S阴影=S△ACO-S扇形COE=AC·OC-=××1-=-π.
∵∠AOC=60°,∴∠COF=120°,
∴的长度为==,
故答案为30°;-π;π.
(2)相切.理由:如图,连接OD,∵AC=BD,AO=OB,OC=OD,∴△AOC≌△BOD,∴∠ACO=∠BDO=90°,∵OD为☉O的半径,∴BD与☉O相切.
6.解析 (1)证明:∵AB是☉O的直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°,∵∠BAC=∠BDA,
∴∠BDA+∠ABC=90°,∴∠BAD=90°,
∴ED是☉O的切线.
(2)∵∠BAC=∠BDA,∠ACB=∠DCA=90°,
∴△ACB∽△DCA,∴==,
∴=,解得BC=2或3,当BC=2时,CD=BD-BC=3,当BC=3时,CD=BD-BC=2,∵AC>CD,∴>CD,∴CD=2,∴BC=3.
(3)证明:由(2)知△ABC∽△DAC,∴=,
∴AC·AD=CD·AB,∵DE·AM=AC·AD,
∴DE·AM=CD·AB,∴=,
∵∠BAM=∠CDE,∴△AMB∽△DCE,
∴∠E=∠ABM,又∵∠EGA=∠BGN,
∴∠BNG=∠GAE=90°,∴BM⊥CE.
素养探究全练
7.解析 (1)证明:连接OD,OC,如图,
∵AD=CD,∴∠AOD=∠DOC,∵四边形ABCD内接于☉O,AB为☉O的直径,∴∠ACB=90°,OC=OA=OB=OD,∴△AOC是等腰三角形,
又∵∠AOD=∠DOC,∴OD垂直平分AC,
∵∠ADM=∠DAC,∴AC∥MN,∴OD⊥MN,即MN是☉O的切线.
(2)证明:连接BD,如图,
∵=,∴∠ABD=∠ACD,∵AC∥MN,
∴∠MNB=∠ACB=90°,∠CDN=∠ACD,∴∠CDN=∠ABD,
∵∠CDN=∠ABD,∠ADB=∠DNC=90°,∴△ABD∽△CDN,∴=,即AD·CD=AB·CN,又∵AD=CD,∴AD2=AB·CN.
(3)令OD与AC交于点H,如图,则∠AHO=90°,
∵∠DCA=∠DBA,∴sin∠DCA=sin∠DBA==,∵AB=6,∴AD=2,易知∠DAC=∠DCA,
∴sin∠DCA=sin∠DAC==,∴DH=2,
在Rt△AHD中,AH==2,
∵AB=6,∴OA=AB=3,∴OH==1,
∵AC∥MN,∴=,∴=,∴AM=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
第二十九章 直线与圆的位置关系
29.3 切线的性质和判定
29.3.2 切线的判定
基础过关全练
知识点 圆的切线的判定
1.【一题多变·切线判定的条件】如图,AB是☉O的直径,连接BT交☉O于点C,连接AC,要使得直线AT是☉O的切线,需要添加的一个条件是 .(写出一个即可)
[变式1·改变特殊角的位置]如图,A、B是☉O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数为 度时,AC才能成为☉O的切线.
[变式2·角度改为距离]如图,已知∠AOB=30°,M为射线OB上任意一点,以M为圆心,2 cm为半径作☉M,当OM= cm时,☉M与OA相切.
2.(2023北京延庆一模)如图,☉O是△ABC的外接圆,AB是直径,OD⊥OC,且∠ADO=∠BOC.
(1)求证:AD是☉O的切线;
(2)若tan∠BAC=,AD=3,求☉O的半径.
能力提升全练
3.【分类讨论思想】(2022河北新河二模,14,★★☆)如图,在直线l上有相距7 cm的两点A和O(点A在点O的右侧),以O为圆心作半径为1 cm的圆,过点A作直线AB⊥l,将☉O以2 cm/s的速度向右移动(点O始终在直线l上),则☉O与直线AB相切时,时间为 ( )
A.3 s B.3.5 s
C.3 s或4 s D.3 s或3.5 s
4. 【新考法】(2023河北武邑二模,16,★★☆)如图,点P在☉O外,连接OP,作OP的垂直平分线MN交OP于点A;以点A为圆心,AO长为半径作☉A,交☉O于点B,C,作直线PC,PB,直线PB交CO的延长线于点D.若BP=8,BD=2,有下列两个结论:①CP是☉O的切线;②☉O的半径为3.对于这两个结论,说法正确的是 ( )
A.①对②不对 B.①不对②对
C.①②均对 D.①②均不对
5.(2023河北石家庄藁城二模,24,★★☆)如图,AB=4,O为AB的中点,以O为圆心,以1为半径画圆交AB于点E,F,过点A作☉O的切线,切点为C,在☉O上取点D,连接BD,使BD=AC.
(1)∠A的度数是 ,阴影部分的面积是 ,的长是 ;
(2)BD与☉O的位置关系是怎样的 说明理由.
6.(2023湖南永州中考,25,★★☆)如图,以AB为直径的☉O是△ABC的外接圆,延长BC到点D,使得∠BAC=∠BDA,点E在DA的延长线上,点M在线段AC上,CE交BM于N,CE交AB于G.
(1)求证:ED是☉O的切线;
(2)若AC=,BD=5,AC>CD,求BC的长;
(3)若DE·AM=AC·AD,求证:BM⊥CE.
素养探究全练
7.【几何直观】(2023四川遂宁中考)如图,四边形ABCD内接于☉O,AB为☉O的直径,AD=CD,过点D的直线l交BA的延长线于点M,交BC的延长线于点N,且∠ADM=∠DAC.
(1)求证:MN是☉O的切线;
(2)求证:AD2=AB·CN;
(3)当AB=6,sin∠DCA=时,求AM的长.
答案全解全析
基础过关全练
1.∠ABT=∠ATB=45°(答案不唯一)
解析 添加条件:∠ABT=∠ATB=45°,
∵∠ABT=∠ATB=45°,∴∠BAT=90°,
又∵AB是圆O的直径,∴AT是圆O的切线,
故答案为∠ABT=∠ATB=45°(答案不唯一).
[变式1] 60
解析 ∵△AOB中,OA=OB,∠AOB=120°,
∴∠OAB=∠OBA=(180°-∠AOB)=30°,
∵当OA⊥AC,即∠OAC=90°时,AC才能成为☉O的切线,∴当∠CAB的度数为60°时,AC才能成为☉O的切线.故答案为60.
[变式2] 4
解析 当☉M与直线OA相切时,过M作MN⊥OA于点N,N为切点,∵∠AOB=30°,∠ONM=90°,∴OM=2MN=4 cm,则当OM=4 cm时,☉M与OA相切.
2.解析 (1)证明:∵OD⊥OC,∴∠DOC=90°,
∴∠AOD+∠BOC=90°.∵∠ADO=∠BOC,
∴∠AOD+∠ADO=90°,∴∠DAO=90°.
∵AB是☉O的直径,∴AD是☉O的切线.
(2)∵AB是☉O的直径,∴∠ACB=90°,∴∠BAC+∠B=90°.过点C作CE⊥AB于点E,∴∠ECB+∠B=90°,∴∠BAC=∠ECB.
∵tan∠BAC=,∴tan∠ECB=.
设BE=a(a>0),则CE=2a,BC=a,
∴AC=2a,AB=5a,∴OA=OB=a,∴OE=a.
∵∠DAO=∠OEC=90°,∠ADO=∠BOC,
∴△ADO∽△EOC,∴=,∴==.
∵AD=3,∴OA=4,即☉O的半径为4.
能力提升全练
3.C 当点O到AB的距离为1 cm时,☉O与AB相切,
∵开始时O点到AB的距离为7 cm,
∴当圆向右移动(7-1)cm或(7+1)cm时,点O到AB的距离为1 cm,此时☉O与AB相切,
∴t==3(s)或t==4(s),即☉O与直线AB在☉O运动3 s或4 s时相切,故选C.
4.A 本题结合尺规作图考查切线的判定.
①∵MN垂直平分OP,交OP于点A,
又以点A为圆心,AO长为半径作☉A,
∴点P在☉A上,OP为☉A的直径,
∴∠PCO=90°,∵OC是☉O的半径,
∴CP是☉O的切线,故①对.
②连接OB,如图,设OB=r,
∵OP为☉A的直径,∴∠PBO=90°,在Rt△PBO和Rt△PCO中,
∴△PBO≌△PCO(HL),
∴PB=PC=8.在△DBO和△DCP中,∠ODB=∠PDC,∠DBO=∠DCP=90°,
∴△DBO∽△DCP,
∴=,即=,∴OD=r.
在Rt△OBD中,OD2=DB2+OB2,
∴=22+r2,解得r=(舍负),故②错误.
故选A.
5.解析 (1)如图,连接OC,
∵AB=4,O为AB的中点,∴AO=BO=2,
∵AC与☉O相切,∴∠ACO=90°,又∵OC=1,
∴sin A==,AC==,
∴∠A=30°,∴∠AOC=60°,
∴S阴影=S△ACO-S扇形COE=AC·OC-=××1-=-π.
∵∠AOC=60°,∴∠COF=120°,
∴的长度为==,
故答案为30°;-π;π.
(2)相切.理由:如图,连接OD,∵AC=BD,AO=OB,OC=OD,∴△AOC≌△BOD,∴∠ACO=∠BDO=90°,∵OD为☉O的半径,∴BD与☉O相切.
6.解析 (1)证明:∵AB是☉O的直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°,∵∠BAC=∠BDA,
∴∠BDA+∠ABC=90°,∴∠BAD=90°,
∴ED是☉O的切线.
(2)∵∠BAC=∠BDA,∠ACB=∠DCA=90°,
∴△ACB∽△DCA,∴==,
∴=,解得BC=2或3,当BC=2时,CD=BD-BC=3,当BC=3时,CD=BD-BC=2,∵AC>CD,∴>CD,∴CD=2,∴BC=3.
(3)证明:由(2)知△ABC∽△DAC,∴=,
∴AC·AD=CD·AB,∵DE·AM=AC·AD,
∴DE·AM=CD·AB,∴=,
∵∠BAM=∠CDE,∴△AMB∽△DCE,
∴∠E=∠ABM,又∵∠EGA=∠BGN,
∴∠BNG=∠GAE=90°,∴BM⊥CE.
素养探究全练
7.解析 (1)证明:连接OD,OC,如图,
∵AD=CD,∴∠AOD=∠DOC,∵四边形ABCD内接于☉O,AB为☉O的直径,∴∠ACB=90°,OC=OA=OB=OD,∴△AOC是等腰三角形,
又∵∠AOD=∠DOC,∴OD垂直平分AC,
∵∠ADM=∠DAC,∴AC∥MN,∴OD⊥MN,即MN是☉O的切线.
(2)证明:连接BD,如图,
∵=,∴∠ABD=∠ACD,∵AC∥MN,
∴∠MNB=∠ACB=90°,∠CDN=∠ACD,∴∠CDN=∠ABD,
∵∠CDN=∠ABD,∠ADB=∠DNC=90°,∴△ABD∽△CDN,∴=,即AD·CD=AB·CN,又∵AD=CD,∴AD2=AB·CN.
(3)令OD与AC交于点H,如图,则∠AHO=90°,
∵∠DCA=∠DBA,∴sin∠DCA=sin∠DBA==,∵AB=6,∴AD=2,易知∠DAC=∠DCA,
∴sin∠DCA=sin∠DAC==,∴DH=2,
在Rt△AHD中,AH==2,
∵AB=6,∴OA=AB=3,∴OH==1,
∵AC∥MN,∴=,∴=,∴AM=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
