29.3.1 切线的性质课时练(含解析)
文档属性
| 名称 | 29.3.1 切线的性质课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 472.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:11:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
第二十九章 直线与圆的位置关系
29.3 切线的性质和判定
29.3.1 切线的性质
基础过关全练
知识点 圆的切线的性质
1.【教材变式·P9T2】如图,点A是☉O上一点,AB切☉O于点A,连接OB交☉O于点C,若∠B=36°,则∠ACO的度数为 ( )
A.63° B.54° C.60° D.126°
2.已知PA,PB是☉O的切线,A,B是切点,点C是☉O上不同于点A、点B的一个动点,若∠APB=54°,则∠ACB的度数是(M9229002) ( )
A.63° B.117°
C.53°或127° D.63°或117°
3.【数形结合思想】如图,点A的坐标为(-3,2),☉A的半径为1,P为坐标轴上一动点,PQ切☉A于点Q,在所有P点中,当PQ的长最小时,点P的坐标为 ( )
A.(0,2) B.(0,3) C.(-2,0) D.(-3,0)
能力提升全练
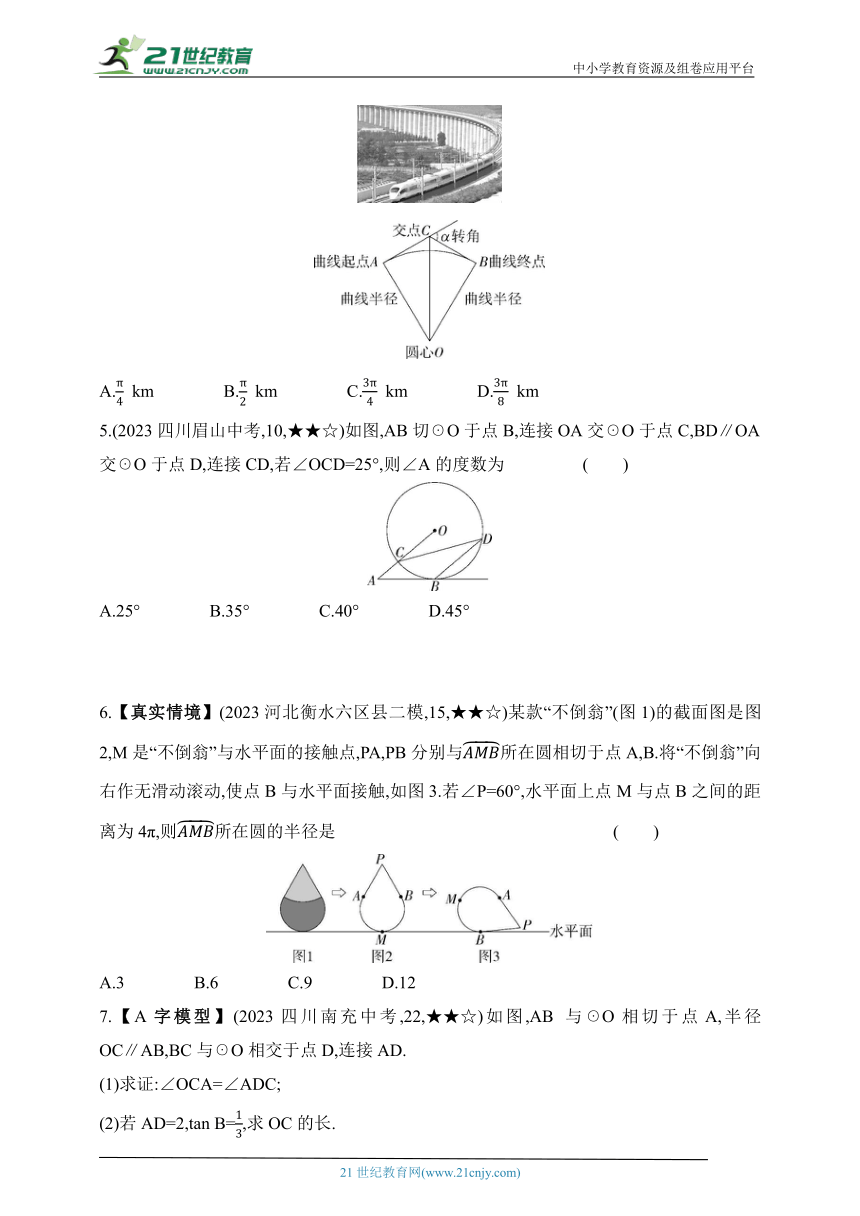
4.【真实情境】(2023山西中考,9,★☆☆)中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图所示的是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.5 km,则这段圆曲线的长为 ( )
A. km B. km C. km D. km
5.(2023四川眉山中考,10,★★☆)如图,AB切☉O于点B,连接OA交☉O于点C,BD∥OA交☉O于点D,连接CD,若∠OCD=25°,则∠A的度数为 ( )
A.25° B.35° C.40° D.45°
6.【真实情境】(2023河北衡水六区县二模,15,★★☆)某款“不倒翁”(图1)的截面图是图2,M是“不倒翁”与水平面的接触点,PA,PB分别与所在圆相切于点A,B.将“不倒翁”向右作无滑动滚动,使点B与水平面接触,如图3.若∠P=60°,水平面上点M与点B之间的距离为4π,则所在圆的半径是 ( )
A.3 B.6 C.9 D.12
7.【A字模型】(2023四川南充中考,22,★★☆)如图,AB 与☉O相切于点A,半径OC∥AB,BC与☉O相交于点D,连接AD.
(1)求证:∠OCA=∠ADC;
(2)若AD=2,tan B=,求OC的长.
8.【河北常考·与圆有关的应用题】(2023河北中考,24,★★☆)装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50 cm,如图1和图2所示,MN为水面截线,GH为台面截线,MN∥GH.
计算 在图1中,已知MN=48 cm,作OC⊥MN于点C.
(1)求OC的长.
操作 将图1中的水槽沿GH向右作无滑动的滚动,使水流出一部分,当∠ANM=30°时停止滚动,如图2.其中,半圆的中点为Q,GH与半圆的切点为E.连接OE交MN于点D.
探究 在图2中,
(2)操作后水面高度下降了多少
(3)连接OQ并延长交GH于点F,求线段EF与的长度,并比较大小.
图1 图2
素养探究全练
9.【几何直观】(2023天津中考)在☉O中,半径OC垂直于弦AB,垂足为D,∠AOC=60°,E为弦AB所对的优弧上一点.
(1)如图1,求∠AOB和∠CEB的大小;
(2)如图2,CE与AB相交于点F,EF=EB,过点E作☉O的切线,与CO的延长线相交于点G,若OA=3,求EG的长.
图1 图2
答案全解全析
基础过关全练
1.A ∵AB切☉O于点A,∴OA⊥AB,∵∠B=36°,
∴∠AOC=90°-∠B=54°,
∵OA=OC,∴∠OAC=∠OCA===63°,故选A.
2.D 如图,连接OA,OB,∵PA,PB是☉O的切线,
∴OA⊥AP,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠APB=54°,
∴∠AOB=126°.
当C在优弧AB上时,∠ACB=∠AOB=63°;
当C'在劣弧AB上时,∠AC'B=180°-∠ACB=117°,则∠ACB的度数为63°或117°.故选D.
3.D 连接AQ、PA,
∵PQ切☉A于点Q,∴AQ⊥PQ,∴∠AQP=90°,
∴PQ==,
当AP的长度最小时,PQ的长度最小,
当AP⊥x轴时,AP的长度最小,PQ的长度最小,
∵A(-3,2),∴P点坐标为(-3,0).故选D.
能力提升全练
4.B ∵α=60°,∴∠ACB=120°,
∵过点A,B的两条切线相交于点C,
∴∠OAC=∠OBC=90°,
∴∠AOB=360°-∠ACB-∠OAC-∠OBC=60°,
∴的长==(km).故选B.
5.C 连接OB,∵AB切☉O于点B,∴∠ABO=90°,∵BD∥OA,∠OCD=25°,∴∠CDB=25°,∴∠BOC=2∠BDC=50°,∴∠A=40°.故选C.
6.B 如图,过A,B作PA,PB的垂线,交于点O,
点O即是所在圆的圆心,设圆的半径为r.
∵∠P=60°,∴∠AOB=120°,
∴∠MOB=∠AOM=120°,
∵水平面上点M与点B之间的距离为4π,
∴的长=4π,∴=4π,解得r=6.故选B.
7.解析 (1)证明:连接OA,如图,
∵AB与☉O相切于点
点A,∴∠OAB=90°,∵OC∥AB,∴∠AOC=90°,∴∠ADC=∠AOC=
45°,∵OC=OA,∴∠OCA=45°,∴∠OCA=∠ADC.
(2)过点A作AH⊥BC于点H,过点C作CF⊥BA交BA的延长线于点F,如图,由(1)得∠ADC=45°,
∴△AHD为等腰直角三角形,∵AD=2,∴AH=DH=,在Rt△ABH中,∵tan B==,∴BH=3,∴AB==2,由(1)得∠AOC=∠OAF=90°,∵CF⊥BA,∴四边形OCFA为矩形,∵OA=OC,∴四边形OCFA为正方形,∴CF=FA=OC,∵∠B=∠B,∠AHB=∠CFB=90°,∴△ABH∽△CBF,∴=,∵BF=AB+AF=2+OC,CF=OC,∴=,解得OC=,经检验,OC=是原方程的解,且符合题意.
8.解析 (1)连接OM,∵O为圆心,OC⊥MN,MN=48 cm,∴MC=MN=24 cm,∵AB=50 cm,∴OM=AB=25 cm,在Rt△OMC中,OC===7(cm).
(2)∵GH与半圆的切点为E,∴OE⊥GH.
∵MN∥GH,∴OE⊥MN,
∵∠ANM=30°,ON=25 cm,∴OD=ON= cm,
∴操作后水面高度下降了-7=(cm).
(3)∵OE⊥MN,∠ANM=30°,
∴∠DOB=60°,∵半圆的中点为Q,∴=,
∴∠QOB=90°,∴∠QOE=∠QOB-∠DOB=30°,
∴EF=OE·tan∠QOE= cm,
的长== cm,
∵-=>0,∴EF的长>的长.
素养探究全练
9.解析 (1)在☉O中,半径OC垂直于弦AB,
∴=,∴∠AOC=∠BOC.
∵∠AOC=60°,∴∠AOB=2∠AOC=120°.
∵∠CEB=∠BOC=∠AOC,∴∠CEB=30°.
(2)连接OE,同(1)得∠CEB=30°.
在△BEF中,∵EF=EB,
∴∠EBF=∠EFB=75°,∴∠AOE=2∠EBA=150°.
又∠AOG=180°-∠AOC=120°,
∴∠GOE=∠AOE-∠AOG=30°.∵GE与☉O相切于点E,∴OE⊥GE,即∠OEG=90°.
在Rt△OEG中,tan∠GOE=,OE=OA=3,
∴EG=3×tan 30°=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
第二十九章 直线与圆的位置关系
29.3 切线的性质和判定
29.3.1 切线的性质
基础过关全练
知识点 圆的切线的性质
1.【教材变式·P9T2】如图,点A是☉O上一点,AB切☉O于点A,连接OB交☉O于点C,若∠B=36°,则∠ACO的度数为 ( )
A.63° B.54° C.60° D.126°
2.已知PA,PB是☉O的切线,A,B是切点,点C是☉O上不同于点A、点B的一个动点,若∠APB=54°,则∠ACB的度数是(M9229002) ( )
A.63° B.117°
C.53°或127° D.63°或117°
3.【数形结合思想】如图,点A的坐标为(-3,2),☉A的半径为1,P为坐标轴上一动点,PQ切☉A于点Q,在所有P点中,当PQ的长最小时,点P的坐标为 ( )
A.(0,2) B.(0,3) C.(-2,0) D.(-3,0)
能力提升全练
4.【真实情境】(2023山西中考,9,★☆☆)中国高铁的飞速发展,已成为中国现代化建设的重要标志.如图所示的是高铁线路在转向处所设计的圆曲线(即圆弧),高铁列车在转弯时的曲线起点为A,曲线终点为B,过点A,B的两条切线相交于点C,列车在从A到B行驶的过程中转角α为60°.若圆曲线的半径OA=1.5 km,则这段圆曲线的长为 ( )
A. km B. km C. km D. km
5.(2023四川眉山中考,10,★★☆)如图,AB切☉O于点B,连接OA交☉O于点C,BD∥OA交☉O于点D,连接CD,若∠OCD=25°,则∠A的度数为 ( )
A.25° B.35° C.40° D.45°
6.【真实情境】(2023河北衡水六区县二模,15,★★☆)某款“不倒翁”(图1)的截面图是图2,M是“不倒翁”与水平面的接触点,PA,PB分别与所在圆相切于点A,B.将“不倒翁”向右作无滑动滚动,使点B与水平面接触,如图3.若∠P=60°,水平面上点M与点B之间的距离为4π,则所在圆的半径是 ( )
A.3 B.6 C.9 D.12
7.【A字模型】(2023四川南充中考,22,★★☆)如图,AB 与☉O相切于点A,半径OC∥AB,BC与☉O相交于点D,连接AD.
(1)求证:∠OCA=∠ADC;
(2)若AD=2,tan B=,求OC的长.
8.【河北常考·与圆有关的应用题】(2023河北中考,24,★★☆)装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50 cm,如图1和图2所示,MN为水面截线,GH为台面截线,MN∥GH.
计算 在图1中,已知MN=48 cm,作OC⊥MN于点C.
(1)求OC的长.
操作 将图1中的水槽沿GH向右作无滑动的滚动,使水流出一部分,当∠ANM=30°时停止滚动,如图2.其中,半圆的中点为Q,GH与半圆的切点为E.连接OE交MN于点D.
探究 在图2中,
(2)操作后水面高度下降了多少
(3)连接OQ并延长交GH于点F,求线段EF与的长度,并比较大小.
图1 图2
素养探究全练
9.【几何直观】(2023天津中考)在☉O中,半径OC垂直于弦AB,垂足为D,∠AOC=60°,E为弦AB所对的优弧上一点.
(1)如图1,求∠AOB和∠CEB的大小;
(2)如图2,CE与AB相交于点F,EF=EB,过点E作☉O的切线,与CO的延长线相交于点G,若OA=3,求EG的长.
图1 图2
答案全解全析
基础过关全练
1.A ∵AB切☉O于点A,∴OA⊥AB,∵∠B=36°,
∴∠AOC=90°-∠B=54°,
∵OA=OC,∴∠OAC=∠OCA===63°,故选A.
2.D 如图,连接OA,OB,∵PA,PB是☉O的切线,
∴OA⊥AP,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠APB=54°,
∴∠AOB=126°.
当C在优弧AB上时,∠ACB=∠AOB=63°;
当C'在劣弧AB上时,∠AC'B=180°-∠ACB=117°,则∠ACB的度数为63°或117°.故选D.
3.D 连接AQ、PA,
∵PQ切☉A于点Q,∴AQ⊥PQ,∴∠AQP=90°,
∴PQ==,
当AP的长度最小时,PQ的长度最小,
当AP⊥x轴时,AP的长度最小,PQ的长度最小,
∵A(-3,2),∴P点坐标为(-3,0).故选D.
能力提升全练
4.B ∵α=60°,∴∠ACB=120°,
∵过点A,B的两条切线相交于点C,
∴∠OAC=∠OBC=90°,
∴∠AOB=360°-∠ACB-∠OAC-∠OBC=60°,
∴的长==(km).故选B.
5.C 连接OB,∵AB切☉O于点B,∴∠ABO=90°,∵BD∥OA,∠OCD=25°,∴∠CDB=25°,∴∠BOC=2∠BDC=50°,∴∠A=40°.故选C.
6.B 如图,过A,B作PA,PB的垂线,交于点O,
点O即是所在圆的圆心,设圆的半径为r.
∵∠P=60°,∴∠AOB=120°,
∴∠MOB=∠AOM=120°,
∵水平面上点M与点B之间的距离为4π,
∴的长=4π,∴=4π,解得r=6.故选B.
7.解析 (1)证明:连接OA,如图,
∵AB与☉O相切于点
点A,∴∠OAB=90°,∵OC∥AB,∴∠AOC=90°,∴∠ADC=∠AOC=
45°,∵OC=OA,∴∠OCA=45°,∴∠OCA=∠ADC.
(2)过点A作AH⊥BC于点H,过点C作CF⊥BA交BA的延长线于点F,如图,由(1)得∠ADC=45°,
∴△AHD为等腰直角三角形,∵AD=2,∴AH=DH=,在Rt△ABH中,∵tan B==,∴BH=3,∴AB==2,由(1)得∠AOC=∠OAF=90°,∵CF⊥BA,∴四边形OCFA为矩形,∵OA=OC,∴四边形OCFA为正方形,∴CF=FA=OC,∵∠B=∠B,∠AHB=∠CFB=90°,∴△ABH∽△CBF,∴=,∵BF=AB+AF=2+OC,CF=OC,∴=,解得OC=,经检验,OC=是原方程的解,且符合题意.
8.解析 (1)连接OM,∵O为圆心,OC⊥MN,MN=48 cm,∴MC=MN=24 cm,∵AB=50 cm,∴OM=AB=25 cm,在Rt△OMC中,OC===7(cm).
(2)∵GH与半圆的切点为E,∴OE⊥GH.
∵MN∥GH,∴OE⊥MN,
∵∠ANM=30°,ON=25 cm,∴OD=ON= cm,
∴操作后水面高度下降了-7=(cm).
(3)∵OE⊥MN,∠ANM=30°,
∴∠DOB=60°,∵半圆的中点为Q,∴=,
∴∠QOB=90°,∴∠QOE=∠QOB-∠DOB=30°,
∴EF=OE·tan∠QOE= cm,
的长== cm,
∵-=>0,∴EF的长>的长.
素养探究全练
9.解析 (1)在☉O中,半径OC垂直于弦AB,
∴=,∴∠AOC=∠BOC.
∵∠AOC=60°,∴∠AOB=2∠AOC=120°.
∵∠CEB=∠BOC=∠AOC,∴∠CEB=30°.
(2)连接OE,同(1)得∠CEB=30°.
在△BEF中,∵EF=EB,
∴∠EBF=∠EFB=75°,∴∠AOE=2∠EBA=150°.
又∠AOG=180°-∠AOC=120°,
∴∠GOE=∠AOE-∠AOG=30°.∵GE与☉O相切于点E,∴OE⊥GE,即∠OEG=90°.
在Rt△OEG中,tan∠GOE=,OE=OA=3,
∴EG=3×tan 30°=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
