30.3 由不共线三点的坐标确定二次函数课时练(含解析)
文档属性
| 名称 | 30.3 由不共线三点的坐标确定二次函数课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 514.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024冀教版数学九年级下学期
第三十章 二次函数
30.3 由不共线三点的坐标确定二次函数*
基础过关全练
知识点 用待定系数法求二次函数的表达式
1.【教材变式·P39例题】已知三点(-1,6)、(0,3)、(1,2),由这三点所确定的二次函数表达式是 ( )
A.y=2x2+3x-1 B.y=x2+4x
C.y=x2-2x+3 D.y=2x2+4x+3
2.【一题多解】如图,抛物线的表达式是 ( )
A.y=x2-x+2 B.y=x2+x+2
C.y=-x2-x+2 D.y=-x2+x+2
3.【待定系数法】二次函数y=ax2+bx+c(a≠0)的x,y的部分对应值如下表所示,则下列判断不正确的是 ( )
x -2 -1 0 1 2
y -2.5 0 1.5 2 1.5
A.当x<0时,y随x的增大而增大
B.当x=4时,y=-2
C.其图像的顶点坐标为(1,2)
D.a=-,c=
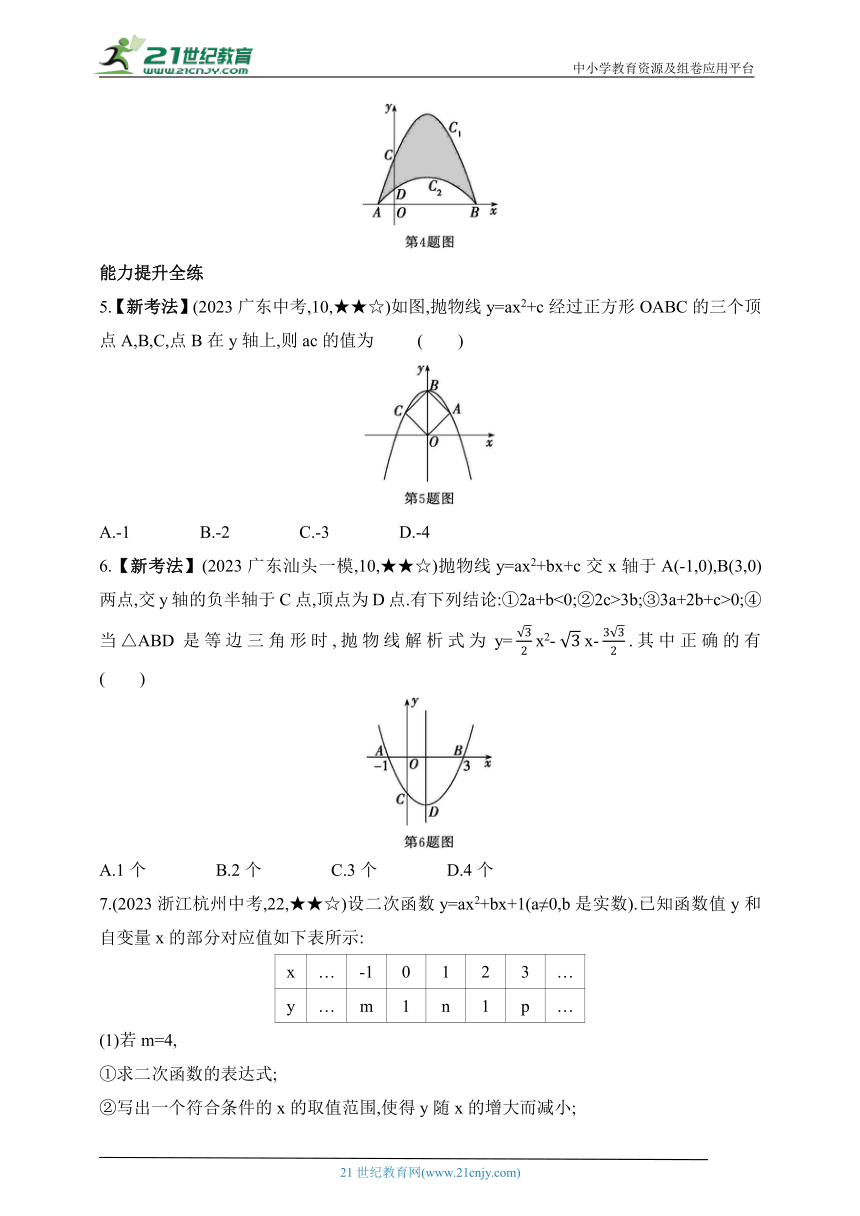
4.【一题多解】【新独家原创】如图,抛物线C1:y=-x2+3x+4与抛物线C2:y=ax2+bx+c组成一个开口向下的“月牙”,抛物线C1和抛物线C2与x轴有着相同的交点A,B(点B在点A右侧),与y轴的交点分别为C,D.如果AD=OD,那么抛物线C2的表达式是 .
能力提升全练
5.【新考法】(2023广东中考,10,★★☆)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为 ( )
A.-1 B.-2 C.-3 D.-4
6.【新考法】(2023广东汕头一模,10,★★☆)抛物线y=ax2+bx+c交x轴于A(-1,0),B(3,0)两点,交y轴的负半轴于C点,顶点为D点.有下列结论:①2a+b<0;②2c>3b;③3a+2b+c>0;④当△ABD是等边三角形时,抛物线解析式为y=x2-x-.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
7.(2023浙江杭州中考,22,★★☆)设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应值如下表所示:
x … -1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小;
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
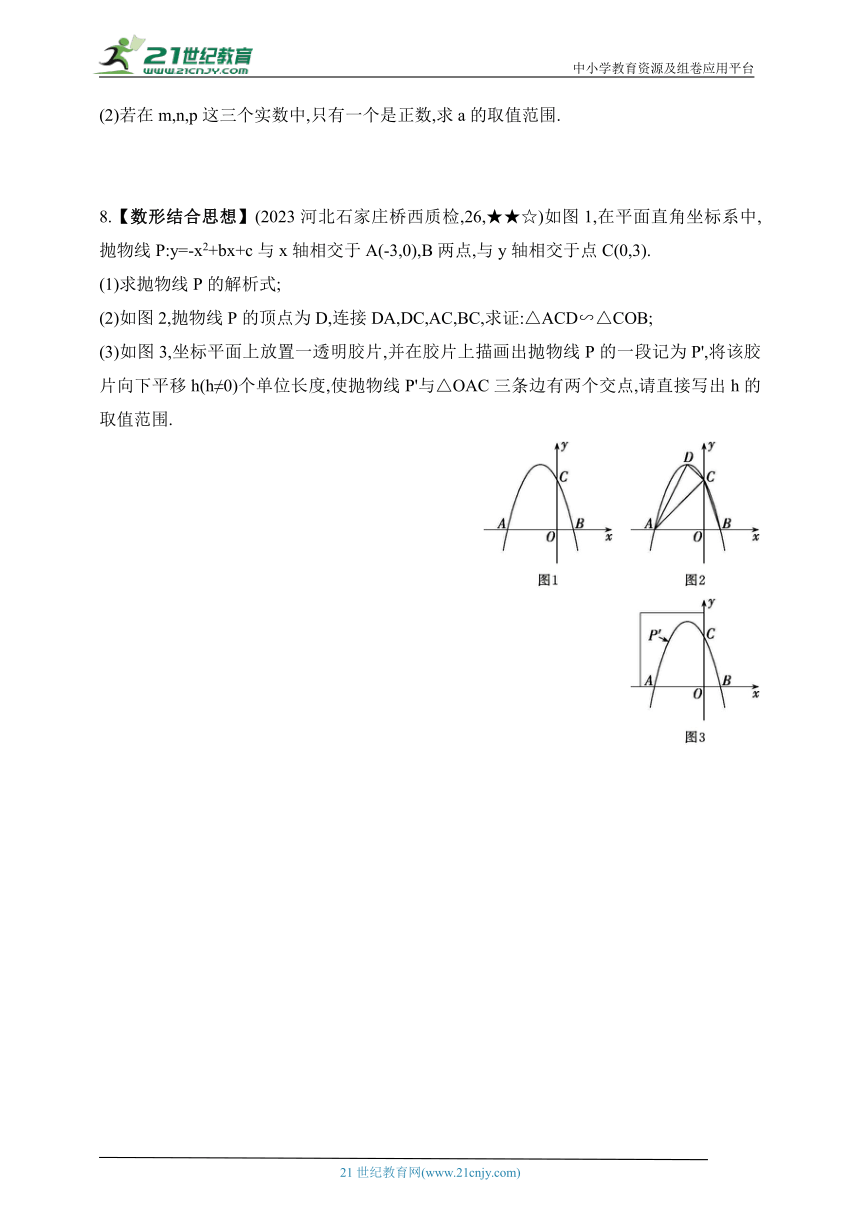
8.【数形结合思想】(2023河北石家庄桥西质检,26,★★☆)如图1,在平面直角坐标系中,抛物线P:y=-x2+bx+c与x轴相交于A(-3,0),B两点,与y轴相交于点C(0,3).
(1)求抛物线P的解析式;
(2)如图2,抛物线P的顶点为D,连接DA,DC,AC,BC,求证:△ACD∽△COB;
(3)如图3,坐标平面上放置一透明胶片,并在胶片上描画出抛物线P的一段记为P',将该胶片向下平移h(h≠0)个单位长度,使抛物线P'与△OAC三条边有两个交点,请直接写出h的取值范围.
素养探究全练
9. 【几何直观】(2022湖南衡阳中考)如图,已知抛物线y=x2-x-2交x轴于A、B两点,将该抛物线位于x轴下方的部分沿x轴翻折,其余部分不变,得到的新图像记为“图像W”,图像W交y轴于点C.
(1)写出图像W位于线段AB上方部分对应的函数关系式;
(2)若直线y=-x+b与图像W有三个交点,请结合图像,直接写出b值;
(3)P为x轴正半轴上一动点,过点P作PM∥y轴交直线BC于点M,交图像W于点N,是否存在这样的点P,使△CMN与△OBC相似 若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
答案全解全析
基础过关全练
1.C 把点(-1,6)、(0,3)、(1,2)的坐标代入y=ax2+bx+c(a≠0),得解得所以y=x2-2x+3,故选C.
方法解读 已知三点求二次函数表达式的方法叫做一般式法.
其步骤如下:①设函数表达式为y=ax2+bx+c(a≠0);
②三点坐标代入后得到一个三元一次方程组;
③解方程组得到a,b,c的值;
④写出函数表达式.
2.D 解法一:根据题意,设抛物线的表达式为y=ax2+bx+c(a≠0),抛物线过点(-1,0),(0,2),(2,0),
所以解得
所以这个抛物线的表达式为y=-x2+x+2.
解法二:根据题意,设抛物线的表达式为y=a(x+1)·(x-2)(a≠0),把(0,2)代入上式,得2=a(0+1)·(0-2),解得a=-1,所以这个抛物线的表达式为y=-(x+1)(x-2)=-x2+x+2.故选D.
3.B 把这三组对应值代入解析式,得解得
∴二次函数y=ax2+bx+c的解析式为y=-x2+x+=-(x-1)2+2,
∴其图像的顶点坐标为(1,2),选项C、D正确,不符合题意;
∵a=-,∴函数图像开口向下,∴x<1时,y随x的增大而增大,∴x<0时,y随x的增大而增大,选项A正确,不符合题意;
当x=4时,y=-×(4-1)2+2=-2.5,选项B不正确,符合题意.故选B.
4. y=-x2+x+1
解析 令-x2+3x+4=0,解得x1=-1,x2=4,
∴A(-1,0),B(4,0),∴OA=1.
在Rt△ADO中,∵AD=OD,∴OD=OA=1,∴c=1.
解法一:将A(-1,0),B(4,0)两点的坐标代入抛物线C2的表达式y=ax2+bx+1中,
得解得
∴抛物线C2的表达式是y=-x2+x+1.
解法二:由抛物线C2过x轴上A,B两点,设抛物线C2的另一个表达式为y=a(x+1)(x-4)=ax2-3ax-4a,∴-4a=c=1,∴a=-,
∴抛物线C2的表达式是y=-x2+x+1.
能力提升全练
5.B 本题综合考查了正方形的性质和求抛物线的系数.连接AC,交y轴于点D,如图所示:
当x=0时,y=c,即OB=c,∵四边形OABC是正方形,∴AC=OB=2AD=2OD=c,AC⊥OB,
∴A,∴=a×+c(*).
由图可知a<0,c>0,化简(*)式得ac=-2,故选B.
6.A 本题结论④结合解直角三角形求点的坐标,将坐标代入解析式,结合a,b,c的关系求抛物线解析式.
∵抛物线y=ax2+bx+c与x轴的交点是A(-1,0),B(3,0),∴抛物线的对称轴为直线x==1,
∴-=1,∴b=-2a,即2a+b=0,故①错误;
∵A(-1,0)在抛物线上,∴a-b+c=0,∴a-(-2a)+c=0,∴c=-3a,∴2c=-6a=3b,故②错误;
3a+2b+c=3a+2(-2a)+(-3a)=-4a,∵抛物线开口向上,∴a>0,∴3a+2b+c=-4a<0,故③错误;
当△ABD是等边三角形时,如图,过D点作DH⊥x轴于H点,
则∠HBD=60°,
又∵HB=AH=2,∴H(1,0),HD=HB·tan∠HBD=2×tan 60°=2,∴D(1,-2).将D点坐标代入二次函数解析式,得a+b+c=-2,又b=-2a,c=-3a,∴a+(-2a)+(-3a)=-2,∴a=,∴b=-,c=,∴抛物线解析式为y=x2-x-,故④正确.综上所述,正确的结论是④,共1个,故选A.
7.解析 (1)①把(-1,4),(2,1)代入y=ax2+bx+1,
得解得
∴y=x2-2x+1.
②∵点(0,1),(2,1)在y=ax2+bx+1的图像上,
∴抛物线的对称轴为直线x==1,
又∵a=1>0,∴当x<1时,y随x的增大而减小,
故此小问答案不唯一,所给范围在x<1范围内即可.
(2)把(2,1)代入y=ax2+bx+1,得1=4a+2b+1,
∴b=-2a,∴y=ax2+bx+1=ax2-2ax+1,
把(-1,m)代入y=ax2-2ax+1,得m=a+2a+1=3a+1,把(1,n)代入y=ax2-2ax+1,得n=a-2a+1=-a+1,把(3,p)代入y=ax2-2ax+1,得p=9a-6a+1=3a+1,∴m=p,
∵在m,n,p这三个实数中,只有一个是正数,
∴解得a≤-.
8.解析 (1)由A,C两点在抛物线上,可得解得
∴抛物线P的解析式为y=-x2-2x+3.
(2)证明:x=-=-1时,y=-1-2×(-1)+3=4,∴D(-1,4),
令-x2-2x+3=0,解得x1=-3,x2=1,∴B(1,0).
由勾股定理得AD=2,CD=,AC=3,BC=,
∴==,==,==,
∴==,
∴△ACD∽△COB.
(3)详解:设直线AC的解析式为y=kx+m(k≠0),
∵A(-3,0),C(0,3),∴解得
∴直线AC的解析式为y=x+3,
根据题意可知:移动前抛物线P'的解析式为y=-x2-2x+3,
向下平移h(h≠0)个单位长度后,解析式为y=-x2-2x+3-h,
当平移后的抛物线P':y=-x2-2x+3-h与直线AC:y=x+3相切时,令-x2-2x+3-h=x+3,
整理,得x2+3x+h=0,
根据相切可知方程有两个相等的解,∴Δ=32-4h=0,∴h=,抛物线P'与y轴交点坐标为,抛物线P'与△OAC三条边有三个交点.
抛物线继续往下移动,当抛物线顶点在OA上时,抛物线P'与△OAC三条边有一个交点.
根据(2)可知:移动前抛物线的顶点坐标为(-1,4),∴抛物线顶点在OA上时,移动的距离h=4,
∴抛物线P'与△OAC三条边有两个交点时,h的取值范围为素养探究全练
9.解析 (1)由题意和翻折的性质可知C(0,2).令x2-x-2=0,解得x1=-1,x2=2,∴A(-1,0),B(2,0),
设图像W中线段AB上方部分对应的解析式为y=a(x+1)(x-2),代入(0,2),解得a=-1,
∴y=-(x+1)(x-2)=-x2+x+2(-1(2)b=2或3.
详解:当直线与(1)中所求部分的图像相切时,有三个交点,联立解析式,得
整理,得x2-2x+b-2=0,由Δ=(-2)2-4(b-2)=0,得b=3,此时方程有两个相等的实数根.
由图像可知,当直线y=-x+b经过点B(2,0)时,直线与图像W有三个交点,此时b=2.
综上,当b=2或b=3时,直线y=-x+b与图像W有三个交点.
(3)存在.由C(0,2),B(2,0)可知△OBC是等腰直角三角形,∴∠OCB=∠OBC=45°.
如图1,当CN∥OB时,△OBC∽△NMC,
此时,N与C关于直线x=-=对称,
∴点N的横坐标为1,∴P(1,0);
如图2,当CN∥OB时,△OBC∽△NMC,此时,N点的纵坐标为2,令x2-x-2=2,解得x1=,x2=(舍),∴点N的横坐标为,
∴P;
如图3,当∠NCM=90°时,△OBC∽△CMN,此时,直线CN的解析式为y=x+2,联立解析式,得解得x1=1+,x2=1-(舍),∴点N的横坐标为1+,∴P(1+,0).
综上所述,P点坐标为(1,0)或或(1+,0).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学九年级下学期
第三十章 二次函数
30.3 由不共线三点的坐标确定二次函数*
基础过关全练
知识点 用待定系数法求二次函数的表达式
1.【教材变式·P39例题】已知三点(-1,6)、(0,3)、(1,2),由这三点所确定的二次函数表达式是 ( )
A.y=2x2+3x-1 B.y=x2+4x
C.y=x2-2x+3 D.y=2x2+4x+3
2.【一题多解】如图,抛物线的表达式是 ( )
A.y=x2-x+2 B.y=x2+x+2
C.y=-x2-x+2 D.y=-x2+x+2
3.【待定系数法】二次函数y=ax2+bx+c(a≠0)的x,y的部分对应值如下表所示,则下列判断不正确的是 ( )
x -2 -1 0 1 2
y -2.5 0 1.5 2 1.5
A.当x<0时,y随x的增大而增大
B.当x=4时,y=-2
C.其图像的顶点坐标为(1,2)
D.a=-,c=
4.【一题多解】【新独家原创】如图,抛物线C1:y=-x2+3x+4与抛物线C2:y=ax2+bx+c组成一个开口向下的“月牙”,抛物线C1和抛物线C2与x轴有着相同的交点A,B(点B在点A右侧),与y轴的交点分别为C,D.如果AD=OD,那么抛物线C2的表达式是 .
能力提升全练
5.【新考法】(2023广东中考,10,★★☆)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为 ( )
A.-1 B.-2 C.-3 D.-4
6.【新考法】(2023广东汕头一模,10,★★☆)抛物线y=ax2+bx+c交x轴于A(-1,0),B(3,0)两点,交y轴的负半轴于C点,顶点为D点.有下列结论:①2a+b<0;②2c>3b;③3a+2b+c>0;④当△ABD是等边三角形时,抛物线解析式为y=x2-x-.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
7.(2023浙江杭州中考,22,★★☆)设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应值如下表所示:
x … -1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小;
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
8.【数形结合思想】(2023河北石家庄桥西质检,26,★★☆)如图1,在平面直角坐标系中,抛物线P:y=-x2+bx+c与x轴相交于A(-3,0),B两点,与y轴相交于点C(0,3).
(1)求抛物线P的解析式;
(2)如图2,抛物线P的顶点为D,连接DA,DC,AC,BC,求证:△ACD∽△COB;
(3)如图3,坐标平面上放置一透明胶片,并在胶片上描画出抛物线P的一段记为P',将该胶片向下平移h(h≠0)个单位长度,使抛物线P'与△OAC三条边有两个交点,请直接写出h的取值范围.
素养探究全练
9. 【几何直观】(2022湖南衡阳中考)如图,已知抛物线y=x2-x-2交x轴于A、B两点,将该抛物线位于x轴下方的部分沿x轴翻折,其余部分不变,得到的新图像记为“图像W”,图像W交y轴于点C.
(1)写出图像W位于线段AB上方部分对应的函数关系式;
(2)若直线y=-x+b与图像W有三个交点,请结合图像,直接写出b值;
(3)P为x轴正半轴上一动点,过点P作PM∥y轴交直线BC于点M,交图像W于点N,是否存在这样的点P,使△CMN与△OBC相似 若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
答案全解全析
基础过关全练
1.C 把点(-1,6)、(0,3)、(1,2)的坐标代入y=ax2+bx+c(a≠0),得解得所以y=x2-2x+3,故选C.
方法解读 已知三点求二次函数表达式的方法叫做一般式法.
其步骤如下:①设函数表达式为y=ax2+bx+c(a≠0);
②三点坐标代入后得到一个三元一次方程组;
③解方程组得到a,b,c的值;
④写出函数表达式.
2.D 解法一:根据题意,设抛物线的表达式为y=ax2+bx+c(a≠0),抛物线过点(-1,0),(0,2),(2,0),
所以解得
所以这个抛物线的表达式为y=-x2+x+2.
解法二:根据题意,设抛物线的表达式为y=a(x+1)·(x-2)(a≠0),把(0,2)代入上式,得2=a(0+1)·(0-2),解得a=-1,所以这个抛物线的表达式为y=-(x+1)(x-2)=-x2+x+2.故选D.
3.B 把这三组对应值代入解析式,得解得
∴二次函数y=ax2+bx+c的解析式为y=-x2+x+=-(x-1)2+2,
∴其图像的顶点坐标为(1,2),选项C、D正确,不符合题意;
∵a=-,∴函数图像开口向下,∴x<1时,y随x的增大而增大,∴x<0时,y随x的增大而增大,选项A正确,不符合题意;
当x=4时,y=-×(4-1)2+2=-2.5,选项B不正确,符合题意.故选B.
4. y=-x2+x+1
解析 令-x2+3x+4=0,解得x1=-1,x2=4,
∴A(-1,0),B(4,0),∴OA=1.
在Rt△ADO中,∵AD=OD,∴OD=OA=1,∴c=1.
解法一:将A(-1,0),B(4,0)两点的坐标代入抛物线C2的表达式y=ax2+bx+1中,
得解得
∴抛物线C2的表达式是y=-x2+x+1.
解法二:由抛物线C2过x轴上A,B两点,设抛物线C2的另一个表达式为y=a(x+1)(x-4)=ax2-3ax-4a,∴-4a=c=1,∴a=-,
∴抛物线C2的表达式是y=-x2+x+1.
能力提升全练
5.B 本题综合考查了正方形的性质和求抛物线的系数.连接AC,交y轴于点D,如图所示:
当x=0时,y=c,即OB=c,∵四边形OABC是正方形,∴AC=OB=2AD=2OD=c,AC⊥OB,
∴A,∴=a×+c(*).
由图可知a<0,c>0,化简(*)式得ac=-2,故选B.
6.A 本题结论④结合解直角三角形求点的坐标,将坐标代入解析式,结合a,b,c的关系求抛物线解析式.
∵抛物线y=ax2+bx+c与x轴的交点是A(-1,0),B(3,0),∴抛物线的对称轴为直线x==1,
∴-=1,∴b=-2a,即2a+b=0,故①错误;
∵A(-1,0)在抛物线上,∴a-b+c=0,∴a-(-2a)+c=0,∴c=-3a,∴2c=-6a=3b,故②错误;
3a+2b+c=3a+2(-2a)+(-3a)=-4a,∵抛物线开口向上,∴a>0,∴3a+2b+c=-4a<0,故③错误;
当△ABD是等边三角形时,如图,过D点作DH⊥x轴于H点,
则∠HBD=60°,
又∵HB=AH=2,∴H(1,0),HD=HB·tan∠HBD=2×tan 60°=2,∴D(1,-2).将D点坐标代入二次函数解析式,得a+b+c=-2,又b=-2a,c=-3a,∴a+(-2a)+(-3a)=-2,∴a=,∴b=-,c=,∴抛物线解析式为y=x2-x-,故④正确.综上所述,正确的结论是④,共1个,故选A.
7.解析 (1)①把(-1,4),(2,1)代入y=ax2+bx+1,
得解得
∴y=x2-2x+1.
②∵点(0,1),(2,1)在y=ax2+bx+1的图像上,
∴抛物线的对称轴为直线x==1,
又∵a=1>0,∴当x<1时,y随x的增大而减小,
故此小问答案不唯一,所给范围在x<1范围内即可.
(2)把(2,1)代入y=ax2+bx+1,得1=4a+2b+1,
∴b=-2a,∴y=ax2+bx+1=ax2-2ax+1,
把(-1,m)代入y=ax2-2ax+1,得m=a+2a+1=3a+1,把(1,n)代入y=ax2-2ax+1,得n=a-2a+1=-a+1,把(3,p)代入y=ax2-2ax+1,得p=9a-6a+1=3a+1,∴m=p,
∵在m,n,p这三个实数中,只有一个是正数,
∴解得a≤-.
8.解析 (1)由A,C两点在抛物线上,可得解得
∴抛物线P的解析式为y=-x2-2x+3.
(2)证明:x=-=-1时,y=-1-2×(-1)+3=4,∴D(-1,4),
令-x2-2x+3=0,解得x1=-3,x2=1,∴B(1,0).
由勾股定理得AD=2,CD=,AC=3,BC=,
∴==,==,==,
∴==,
∴△ACD∽△COB.
(3)
∵A(-3,0),C(0,3),∴解得
∴直线AC的解析式为y=x+3,
根据题意可知:移动前抛物线P'的解析式为y=-x2-2x+3,
向下平移h(h≠0)个单位长度后,解析式为y=-x2-2x+3-h,
当平移后的抛物线P':y=-x2-2x+3-h与直线AC:y=x+3相切时,令-x2-2x+3-h=x+3,
整理,得x2+3x+h=0,
根据相切可知方程有两个相等的解,∴Δ=32-4h=0,∴h=,抛物线P'与y轴交点坐标为,抛物线P'与△OAC三条边有三个交点.
抛物线继续往下移动,当抛物线顶点在OA上时,抛物线P'与△OAC三条边有一个交点.
根据(2)可知:移动前抛物线的顶点坐标为(-1,4),∴抛物线顶点在OA上时,移动的距离h=4,
∴抛物线P'与△OAC三条边有两个交点时,h的取值范围为
9.解析 (1)由题意和翻折的性质可知C(0,2).令x2-x-2=0,解得x1=-1,x2=2,∴A(-1,0),B(2,0),
设图像W中线段AB上方部分对应的解析式为y=a(x+1)(x-2),代入(0,2),解得a=-1,
∴y=-(x+1)(x-2)=-x2+x+2(-1
详解:当直线与(1)中所求部分的图像相切时,有三个交点,联立解析式,得
整理,得x2-2x+b-2=0,由Δ=(-2)2-4(b-2)=0,得b=3,此时方程有两个相等的实数根.
由图像可知,当直线y=-x+b经过点B(2,0)时,直线与图像W有三个交点,此时b=2.
综上,当b=2或b=3时,直线y=-x+b与图像W有三个交点.
(3)存在.由C(0,2),B(2,0)可知△OBC是等腰直角三角形,∴∠OCB=∠OBC=45°.
如图1,当CN∥OB时,△OBC∽△NMC,
此时,N与C关于直线x=-=对称,
∴点N的横坐标为1,∴P(1,0);
如图2,当CN∥OB时,△OBC∽△NMC,此时,N点的纵坐标为2,令x2-x-2=2,解得x1=,x2=(舍),∴点N的横坐标为,
∴P;
如图3,当∠NCM=90°时,△OBC∽△CMN,此时,直线CN的解析式为y=x+2,联立解析式,得解得x1=1+,x2=1-(舍),∴点N的横坐标为1+,∴P(1+,0).
综上所述,P点坐标为(1,0)或或(1+,0).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
