2024鲁教版五四制数学九年级下学期课时练--专项素养综合全练(三)常考辅助圆模型(含解析)
文档属性
| 名称 | 2024鲁教版五四制数学九年级下学期课时练--专项素养综合全练(三)常考辅助圆模型(含解析) | 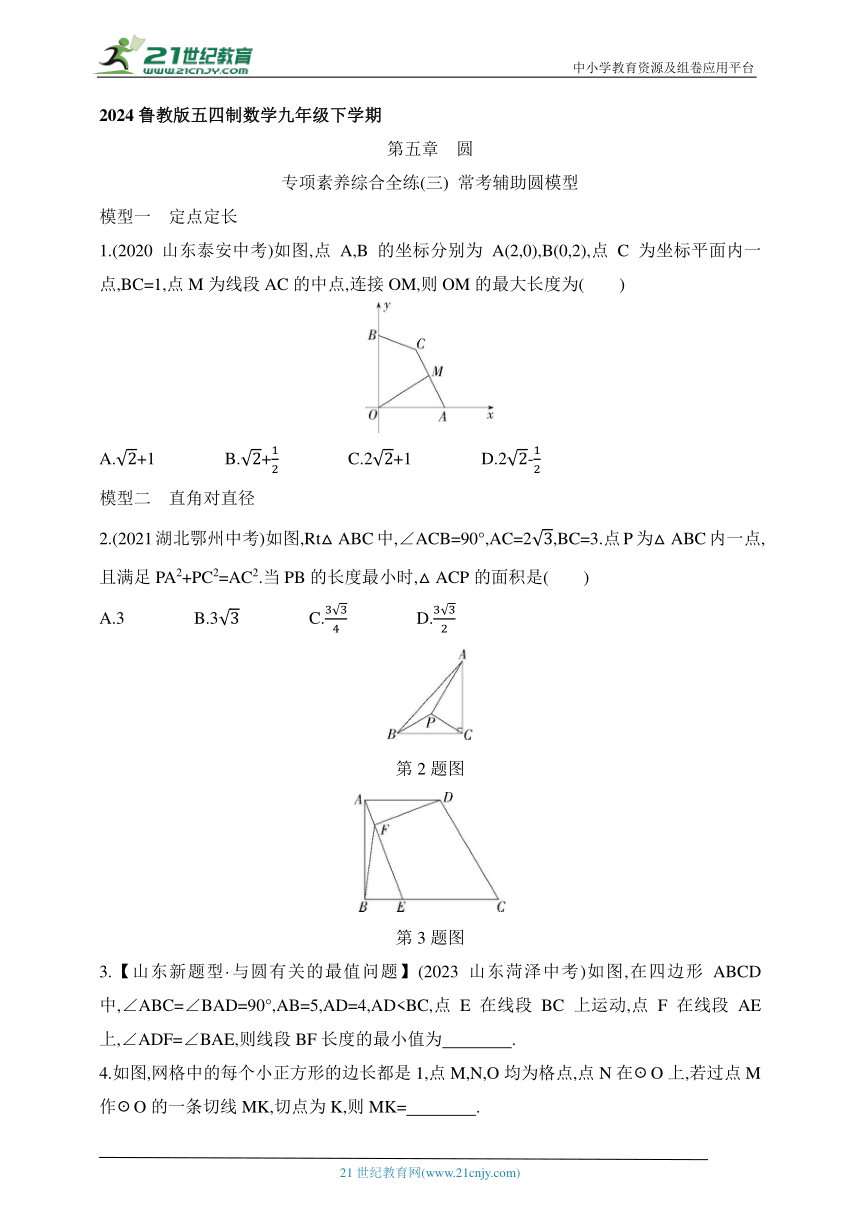 | |
| 格式 | docx | ||
| 文件大小 | 550.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:18:32 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
圆
专项素养综合全练(三) 常考辅助圆模型
模型一 定点定长
1.(2020山东泰安中考)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大长度为( )
A.+1 B.+ C.2+1 D.2-
模型二 直角对直径
2.(2021湖北鄂州中考)如图,Rt△ABC中,∠ACB=90°,AC=2,BC=3.点P为△ABC内一点,且满足PA2+PC2=AC2.当PB的长度最小时,△ACP的面积是( )
A.3 B.3 C. D.
第2题图
第3题图
3.【山东新题型·与圆有关的最值问题】(2023山东菏泽中考)如图,在四边形ABCD中,∠ABC=∠BAD=90°,AB=5,AD=4,AD4.如图,网格中的每个小正方形的边长都是1,点M,N,O均为格点,点N在☉O上,若过点M作☉O的一条切线MK,切点为K,则MK= .
5.【阅读】
辅助线是几何解题中条件与结论的桥梁.在众多类型的辅助线中,辅助圆作为一条曲线型辅助线,显得独特而隐蔽.
性质:如图①,若∠ACB=∠ADB=90°,则点D在经过A,B,C三点的圆上.
【问题解决】
运用上述材料中的信息解决以下问题:
(1)如图②,已知DA=DB=DC.
求证:∠ADB=2∠ACB.
(2)如图③,点A,B位于直线l两侧.用尺规在直线l上作出点C,使得∠ACB=90°.(要求:要有画图痕迹,不用写画法)
(3)如图④,在四边形ABCD中,∠CAD=90°,CB⊥DB,点F在CA的延长线上,连接DF,∠ADF=∠ABD.
求证:DF是△ACD外接圆的切线.
模型三 点圆最值
6.【山东新题型·与圆有关的最值问题】(2023山东泰安泰山期末)如图,点P(3,4),☉P的半径为2,A(2.5,0),B(5,0),点M是☉P上的动点,点C是MB的中点,则AC长的最大值是( )
A. B. C. D.
模型四 线圆最值
7.(2023四川乐山中考)如图,在平面直角坐标系xOy中,直线y=-x-2与x轴,y轴分别交于A,B两点,C,D是半径为1的☉O上两动点,且CD=,P为弦CD的中点.当C,D两点在圆上运动时,△PAB面积的最大值是( )
A.8 B.6 C.4 D.3
第7题图
第8题图
8.(2020山东东营中考)如图,在Rt△AOB中,OB=2,∠A=30°,☉O的半径为1,点P是AB边上的动点,过点P作☉O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 .
模型五 定弦定角
9.(2023北京昌平二模)船航行的海岸附近有暗礁,为了使船不触上暗礁,可以在暗礁的两侧建立两座灯塔.只要留心从船上到两座灯塔间的角度不超过一定的大小,就不用担心触礁.如图所示的网格是正方形网格,点A,B,C,D,P,M,N是网格线交点,当船航行到点P的位置时,P与两座灯塔M,N间的角度(∠MPN的大小)一定无触礁危险.那么,对于A,B,C,D四个位置,船处于 时,一定无触礁危险.( )
A.位置A B.位置B
C.位置C D.位置D
10.(2021广东中考)在△ABC中,∠ABC=90°,AB=2,BC=3.点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为 .
11.(2023四川自贡中考改编)如图,分别经过原点O和点A(4,0)的动直线a,b的夹角∠OBA=30°,点M是OB的中点,连接AM,则当sin∠OAM取最大值时,AM= .
答案全解全析
1.B ∵点C为坐标平面内一点,BC=1,
∴点C在半径为1的☉B上.
在x轴负半轴上取OD=OA=2,连接BD,如图,
∵AM=CM,OA=DO,∴OM=CD.
∴当CD长的值最大时,OM长的值最大.
∴当C在DB的延长线上时,OM长的值最大.
∵OB=OD=2,∠BOD=90°,∴BD=2.
∴CD长的最大值=2+1.
∴OM长的最大值=CD=+.
2.D ∵PA2+PC2=AC2,∴∠APC=90°.
∴点P在以AC为直径的圆上运动.
添加辅助圆(圆O),连接OP,如图所示.
当点P在线段BO上时,PB长有最小值,
此时PO=AO=CO=AC=×2=.
∵tan∠BOC===,∴∠BOC=60°.
过P作PH⊥AC于H,
∴△ACP的面积=AC·PH=AC·OP·sin∠BOC=×2××=.故选D.
3.答案-2
解析如图,设AD的中点为O,以AD为直径画圆,连接OB交☉O于F'.
∵∠ABC+∠BAD=90°+90°=180°,
∴AD∥BC.∴∠DAE=∠AEB.
∵∠ADF=∠BAE,∴∠DFA=∠ABE=90°.
∴点F在以AD为直径的半圆上运动,当点F运动到OB与☉O的交点(F')处时,线段BF的长度取最小值.
∵AD=4,∴AO=OF'=AD=2.
∴BO==,
∴线段BF的长度的最小值为-2.
经典模型 直角对直径模型
在解决一类单或双动点求最值的问题时,若存在某动点为直角的顶点,则往往根据直角对直径构造辅助圆,将该动点转化为半圆上的动点,从而将最值问题转化为点圆的最值问题解决.
4.答案2
解析如图所示,以OM为直径作圆,与☉O的交点即为切点K,连接OK,ON.则OK⊥MK.
由网格特点及勾股定理可得MO=5,OK=ON=,
∴MK==2.
5.解析(1)证明:如图,由DA=DB=DC可知,点A,B,C在以D为圆心,DA的长为半径的圆上,
∴∠ADB=2∠ACB.
(2)如图,点C1,C2就是所要求作的点.
(3)证明:如图,以CD的中点O为圆心,CD为直径作☉O,
∵∠DAC=∠DBC=90°,∴点A,B在☉O上,
即☉O是△ACD的外接圆.
∴∠ACD=∠ABD.∵∠ADF=∠ABD,
∴∠ACD=∠ADF.
∵∠ACD+∠ADC=90°,∴∠ADF+∠ADC=90°.
∴∠CDF=90°.∴CD⊥DF.
∴DF是△ACD外接圆的切线.
6.C 如图,作射线OP,交☉P于M1,M2,连接OM.
由勾股定理得OP==5.
∵A(2.5,0),B(5,0),∴OA=AB,
又CM=CB,∴AC=OM.
∴当OM长最大时,AC长最大.
当M运动到M2时,OM最大,
∴AC长的最大值=OM2=(OP+PM2)=×(5+2)=,故选C.
7.D 如图,作OQ⊥AB于点Q,连接OP,OD,OC,
∵CD=,OC=OD=1,∴OC2+OD2=CD2.
∴△OCD为等腰直角三角形.
由y=-x-2得,点A(-2,0),B(0,-2),
∴OA=OB=2.∴△OAB为等腰直角三角形.
∴AB=2,OQ=.
∵P为CD的中点,∴OP=.
点P的运动轨迹是以O为圆心,以为半径的圆.
当P,O,Q共线,且P,Q在点O两侧时,S△ABP最大,
此时PQ=OP+OQ=,∴S△ABP=AB·PQ=3.故选D.
8.答案2
解析如图,连接OQ,OP.
∵PQ是☉O的切线,∴∠OQP=90°.
∴PQ==.
∴当线段OP的长度最小时,线段PQ的长度最小,当OP⊥AB时,线段OP的长度最小,
此时OP=OB·sin B.
∵在Rt△AOB中,∠B=90°-∠A=90°-30°=60°,
∴线段OP长度的最小值=2×=3.
∴线段PQ长度的最小值==2.
9.B 如图,
由网格特点可知,点O是MN和MP的垂直平分线的交点,即点O是△MNP的外接圆的圆心.
由画图知点B在△MNP的外接圆上.
连接BM,BN,则∠MPN=∠MBN.
∴船处于位置B时,一定无触礁危险,故选B.
10.答案-
解析如图所示,作△ABD的外接圆☉O,连接OA,OB,OC,设OC与☉O交于点D',则CD'的长度即为CD长度的最小值.
∵∠ADB=45°,∴∠AOB=90°.
∵OA=OB,∴△AOB为等腰直角三角形.
∴AO=BO=AB·sin 45°=,∴OD'=.
∵∠OBA=45°,∠ABC=90°,∴∠OBC=45°.
作OE⊥BC于点E,则△OBE为等腰直角三角形.
∴OE=BE=OB·sin 45°=1,∴CE=BC-BE=3-1=2.
在Rt△OCE中,OC===.
∴CD'=OC-OD'=-.
∴线段CD长度的最小值为-.
11.答案2
解析如图,作△AOB的外接圆☉T,连接OT,TA,TB,取OT的中点K,连接KM,AK.
∵∠ATO=2∠ABO,∴∠ATO=60°,∵TO=TA,
∴△OAT是等边三角形.
∵A(4,0),∴TO=TA=TB=4.
∵OK=KT,OM=MB,∴KM=TB=2.
∴点M在以K为圆心,2为半径的圆上运动.
当AM与☉K相切时,∠OAM最大,此时sin∠OAM的值最大.
∵△OTA是等边三角形,OK=KT,∴AK⊥OT.
∴AK===2.
∵AM是☉K的切线,KM是☉K的半径,∴AM⊥KM.
∴AM===2.
经典模型 定弦对定角模型
在同圆或等圆中,同一条弦所对的劣弧(或优弧)上的圆周角都相等.反过来,若某线段所对同一侧的角都相等,则这些角的顶点都在同一圆上,据此常构造辅助圆解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
圆
专项素养综合全练(三) 常考辅助圆模型
模型一 定点定长
1.(2020山东泰安中考)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大长度为( )
A.+1 B.+ C.2+1 D.2-
模型二 直角对直径
2.(2021湖北鄂州中考)如图,Rt△ABC中,∠ACB=90°,AC=2,BC=3.点P为△ABC内一点,且满足PA2+PC2=AC2.当PB的长度最小时,△ACP的面积是( )
A.3 B.3 C. D.
第2题图
第3题图
3.【山东新题型·与圆有关的最值问题】(2023山东菏泽中考)如图,在四边形ABCD中,∠ABC=∠BAD=90°,AB=5,AD=4,AD
5.【阅读】
辅助线是几何解题中条件与结论的桥梁.在众多类型的辅助线中,辅助圆作为一条曲线型辅助线,显得独特而隐蔽.
性质:如图①,若∠ACB=∠ADB=90°,则点D在经过A,B,C三点的圆上.
【问题解决】
运用上述材料中的信息解决以下问题:
(1)如图②,已知DA=DB=DC.
求证:∠ADB=2∠ACB.
(2)如图③,点A,B位于直线l两侧.用尺规在直线l上作出点C,使得∠ACB=90°.(要求:要有画图痕迹,不用写画法)
(3)如图④,在四边形ABCD中,∠CAD=90°,CB⊥DB,点F在CA的延长线上,连接DF,∠ADF=∠ABD.
求证:DF是△ACD外接圆的切线.
模型三 点圆最值
6.【山东新题型·与圆有关的最值问题】(2023山东泰安泰山期末)如图,点P(3,4),☉P的半径为2,A(2.5,0),B(5,0),点M是☉P上的动点,点C是MB的中点,则AC长的最大值是( )
A. B. C. D.
模型四 线圆最值
7.(2023四川乐山中考)如图,在平面直角坐标系xOy中,直线y=-x-2与x轴,y轴分别交于A,B两点,C,D是半径为1的☉O上两动点,且CD=,P为弦CD的中点.当C,D两点在圆上运动时,△PAB面积的最大值是( )
A.8 B.6 C.4 D.3
第7题图
第8题图
8.(2020山东东营中考)如图,在Rt△AOB中,OB=2,∠A=30°,☉O的半径为1,点P是AB边上的动点,过点P作☉O的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为 .
模型五 定弦定角
9.(2023北京昌平二模)船航行的海岸附近有暗礁,为了使船不触上暗礁,可以在暗礁的两侧建立两座灯塔.只要留心从船上到两座灯塔间的角度不超过一定的大小,就不用担心触礁.如图所示的网格是正方形网格,点A,B,C,D,P,M,N是网格线交点,当船航行到点P的位置时,P与两座灯塔M,N间的角度(∠MPN的大小)一定无触礁危险.那么,对于A,B,C,D四个位置,船处于 时,一定无触礁危险.( )
A.位置A B.位置B
C.位置C D.位置D
10.(2021广东中考)在△ABC中,∠ABC=90°,AB=2,BC=3.点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为 .
11.(2023四川自贡中考改编)如图,分别经过原点O和点A(4,0)的动直线a,b的夹角∠OBA=30°,点M是OB的中点,连接AM,则当sin∠OAM取最大值时,AM= .
答案全解全析
1.B ∵点C为坐标平面内一点,BC=1,
∴点C在半径为1的☉B上.
在x轴负半轴上取OD=OA=2,连接BD,如图,
∵AM=CM,OA=DO,∴OM=CD.
∴当CD长的值最大时,OM长的值最大.
∴当C在DB的延长线上时,OM长的值最大.
∵OB=OD=2,∠BOD=90°,∴BD=2.
∴CD长的最大值=2+1.
∴OM长的最大值=CD=+.
2.D ∵PA2+PC2=AC2,∴∠APC=90°.
∴点P在以AC为直径的圆上运动.
添加辅助圆(圆O),连接OP,如图所示.
当点P在线段BO上时,PB长有最小值,
此时PO=AO=CO=AC=×2=.
∵tan∠BOC===,∴∠BOC=60°.
过P作PH⊥AC于H,
∴△ACP的面积=AC·PH=AC·OP·sin∠BOC=×2××=.故选D.
3.答案-2
解析如图,设AD的中点为O,以AD为直径画圆,连接OB交☉O于F'.
∵∠ABC+∠BAD=90°+90°=180°,
∴AD∥BC.∴∠DAE=∠AEB.
∵∠ADF=∠BAE,∴∠DFA=∠ABE=90°.
∴点F在以AD为直径的半圆上运动,当点F运动到OB与☉O的交点(F')处时,线段BF的长度取最小值.
∵AD=4,∴AO=OF'=AD=2.
∴BO==,
∴线段BF的长度的最小值为-2.
经典模型 直角对直径模型
在解决一类单或双动点求最值的问题时,若存在某动点为直角的顶点,则往往根据直角对直径构造辅助圆,将该动点转化为半圆上的动点,从而将最值问题转化为点圆的最值问题解决.
4.答案2
解析如图所示,以OM为直径作圆,与☉O的交点即为切点K,连接OK,ON.则OK⊥MK.
由网格特点及勾股定理可得MO=5,OK=ON=,
∴MK==2.
5.解析(1)证明:如图,由DA=DB=DC可知,点A,B,C在以D为圆心,DA的长为半径的圆上,
∴∠ADB=2∠ACB.
(2)如图,点C1,C2就是所要求作的点.
(3)证明:如图,以CD的中点O为圆心,CD为直径作☉O,
∵∠DAC=∠DBC=90°,∴点A,B在☉O上,
即☉O是△ACD的外接圆.
∴∠ACD=∠ABD.∵∠ADF=∠ABD,
∴∠ACD=∠ADF.
∵∠ACD+∠ADC=90°,∴∠ADF+∠ADC=90°.
∴∠CDF=90°.∴CD⊥DF.
∴DF是△ACD外接圆的切线.
6.C 如图,作射线OP,交☉P于M1,M2,连接OM.
由勾股定理得OP==5.
∵A(2.5,0),B(5,0),∴OA=AB,
又CM=CB,∴AC=OM.
∴当OM长最大时,AC长最大.
当M运动到M2时,OM最大,
∴AC长的最大值=OM2=(OP+PM2)=×(5+2)=,故选C.
7.D 如图,作OQ⊥AB于点Q,连接OP,OD,OC,
∵CD=,OC=OD=1,∴OC2+OD2=CD2.
∴△OCD为等腰直角三角形.
由y=-x-2得,点A(-2,0),B(0,-2),
∴OA=OB=2.∴△OAB为等腰直角三角形.
∴AB=2,OQ=.
∵P为CD的中点,∴OP=.
点P的运动轨迹是以O为圆心,以为半径的圆.
当P,O,Q共线,且P,Q在点O两侧时,S△ABP最大,
此时PQ=OP+OQ=,∴S△ABP=AB·PQ=3.故选D.
8.答案2
解析如图,连接OQ,OP.
∵PQ是☉O的切线,∴∠OQP=90°.
∴PQ==.
∴当线段OP的长度最小时,线段PQ的长度最小,当OP⊥AB时,线段OP的长度最小,
此时OP=OB·sin B.
∵在Rt△AOB中,∠B=90°-∠A=90°-30°=60°,
∴线段OP长度的最小值=2×=3.
∴线段PQ长度的最小值==2.
9.B 如图,
由网格特点可知,点O是MN和MP的垂直平分线的交点,即点O是△MNP的外接圆的圆心.
由画图知点B在△MNP的外接圆上.
连接BM,BN,则∠MPN=∠MBN.
∴船处于位置B时,一定无触礁危险,故选B.
10.答案-
解析如图所示,作△ABD的外接圆☉O,连接OA,OB,OC,设OC与☉O交于点D',则CD'的长度即为CD长度的最小值.
∵∠ADB=45°,∴∠AOB=90°.
∵OA=OB,∴△AOB为等腰直角三角形.
∴AO=BO=AB·sin 45°=,∴OD'=.
∵∠OBA=45°,∠ABC=90°,∴∠OBC=45°.
作OE⊥BC于点E,则△OBE为等腰直角三角形.
∴OE=BE=OB·sin 45°=1,∴CE=BC-BE=3-1=2.
在Rt△OCE中,OC===.
∴CD'=OC-OD'=-.
∴线段CD长度的最小值为-.
11.答案2
解析如图,作△AOB的外接圆☉T,连接OT,TA,TB,取OT的中点K,连接KM,AK.
∵∠ATO=2∠ABO,∴∠ATO=60°,∵TO=TA,
∴△OAT是等边三角形.
∵A(4,0),∴TO=TA=TB=4.
∵OK=KT,OM=MB,∴KM=TB=2.
∴点M在以K为圆心,2为半径的圆上运动.
当AM与☉K相切时,∠OAM最大,此时sin∠OAM的值最大.
∵△OTA是等边三角形,OK=KT,∴AK⊥OT.
∴AK===2.
∵AM是☉K的切线,KM是☉K的半径,∴AM⊥KM.
∴AM===2.
经典模型 定弦对定角模型
在同圆或等圆中,同一条弦所对的劣弧(或优弧)上的圆周角都相等.反过来,若某线段所对同一侧的角都相等,则这些角的顶点都在同一圆上,据此常构造辅助圆解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
