2024鲁教版五四制数学九年级下学期课时练--专项素养综合全练(五)圆的综合探究题(含解析)
文档属性
| 名称 | 2024鲁教版五四制数学九年级下学期课时练--专项素养综合全练(五)圆的综合探究题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 429.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
圆
专项素养综合全练(五) 圆的综合探究题
类型一 圆性质的综合探究题
1.(2023山东威海文登期末)
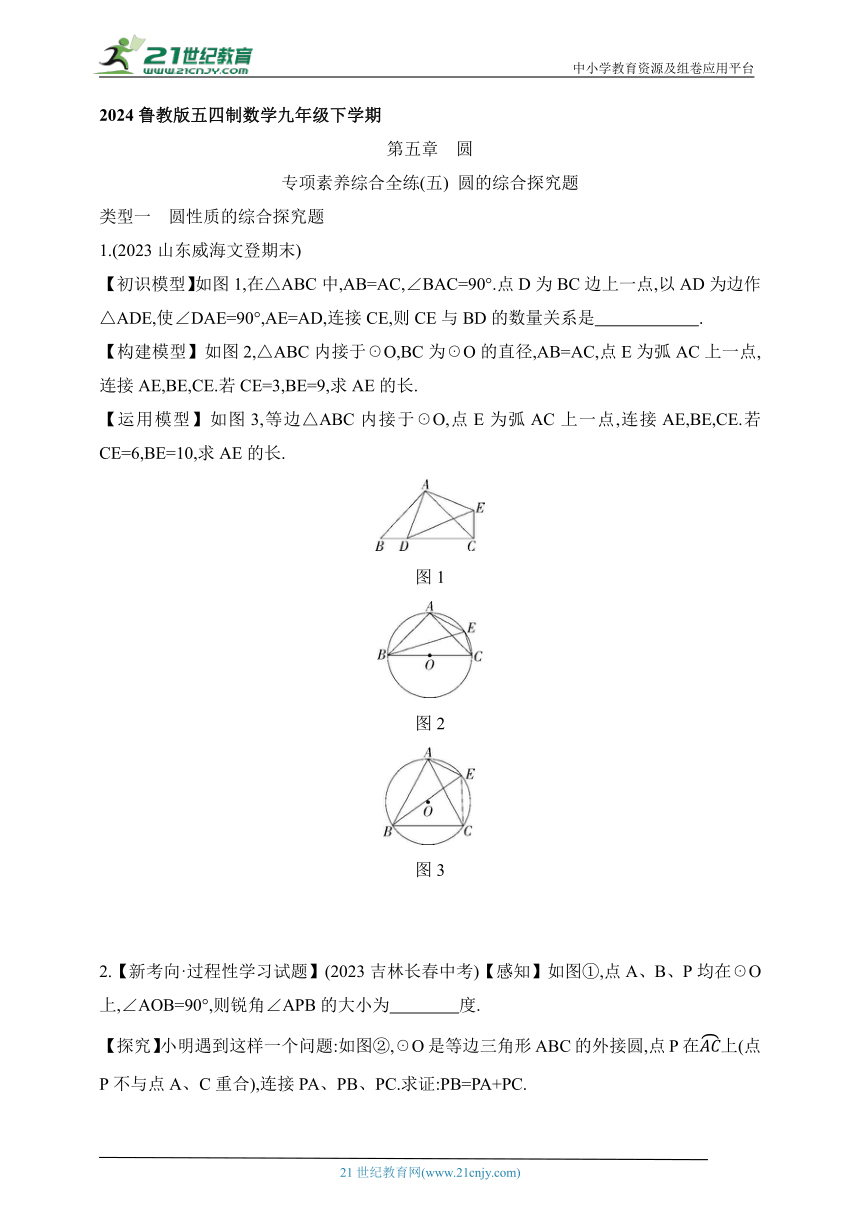
【初识模型】如图1,在△ABC中,AB=AC,∠BAC=90°.点D为BC边上一点,以AD为边作△ADE,使∠DAE=90°,AE=AD,连接CE,则CE与BD的数量关系是 .
【构建模型】如图2,△ABC内接于☉O,BC为☉O的直径,AB=AC,点E为弧AC上一点,连接AE,BE,CE.若CE=3,BE=9,求AE的长.
【运用模型】如图3,等边△ABC内接于☉O,点E为弧AC上一点,连接AE,BE,CE.若CE=6,BE=10,求AE的长.
图1
图2
图3
2.【新考向·过程性学习试题】(2023吉林长春中考)【感知】如图①,点A、B、P均在☉O上,∠AOB=90°,则锐角∠APB的大小为 度.
【探究】小明遇到这样一个问题:如图②,☉O是等边三角形ABC的外接圆,点P在上(点P不与点A、C重合),连接PA、PB、PC.求证:PB=PA+PC.
小明发现,延长PA至点E,使AE=PC,连接BE,通过证明△PBC≌△EBA可推得△PBE是等边三角形,进而得证.下面是小明的部分证明过程:
证明:延长PA至点E,使AE=PC,连接BE.
∵四边形ABCP是☉O的内接四边形,
∴∠BAP+∠BCP=180°,
∵∠BAP+∠BAE=180°,
∴∠BCP=∠BAE,
∵△ABC是等边三角形,
∴BA=BC,
∴△PBC≌△EBA(SAS).
请你补全余下的证明过程.
【应用】如图③,☉O是△ABC的外接圆,∠ABC=90°,AB=BC,点P在☉O上,且点P与点B在AC的两侧,连接PA、PB、PC,若PB=2PA,则的值为 .
图①
图②
图③
类型二 圆位置关系的综合探究题
3.(2023陕西中考A卷)(1)如图①,在△OAB中,OA=OB,∠AOB=120°,AB=24.若☉O的半径为4,点P在☉O上,点M在AB上,连接PM,求线段PM长度的最小值.
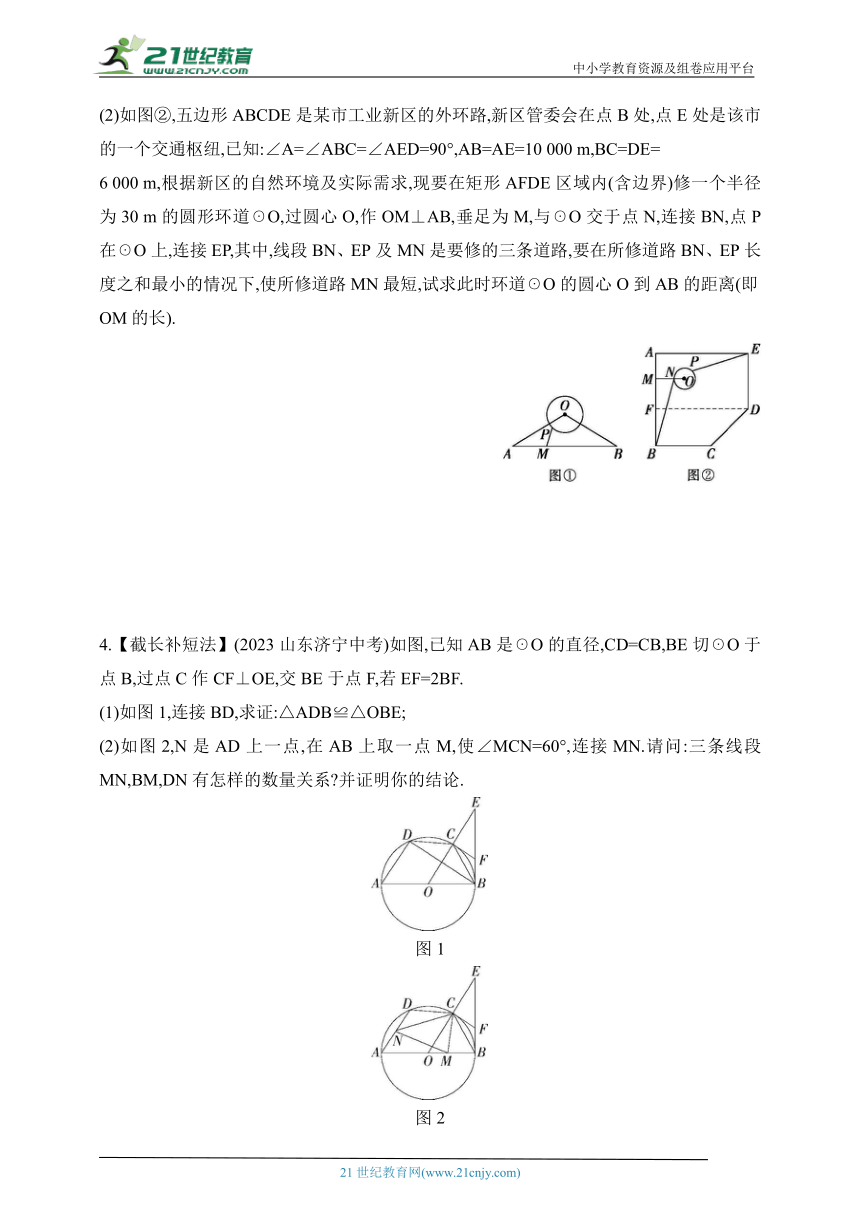
(2)如图②,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的一个交通枢纽,已知:∠A=∠ABC=∠AED=90°,AB=AE=10 000 m,BC=DE=
6 000 m,根据新区的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修一个半径为30 m的圆形环道☉O,过圆心O,作OM⊥AB,垂足为M,与☉O交于点N,连接BN,点P在☉O上,连接EP,其中,线段BN、EP及MN是要修的三条道路,要在所修道路BN、EP长度之和最小的情况下,使所修道路MN最短,试求此时环道☉O的圆心O到AB的距离(即OM的长).
4.【截长补短法】(2023山东济宁中考)如图,已知AB是☉O的直径,CD=CB,BE切☉O于点B,过点C作CF⊥OE,交BE于点F,若EF=2BF.
(1)如图1,连接BD,求证:△ADB≌△OBE;
(2)如图2,N是AD上一点,在AB上取一点M,使∠MCN=60°,连接MN.请问:三条线段MN,BM,DN有怎样的数量关系 并证明你的结论.
图1
图2
答案全解全析
1.解析【初识模型】CE=BD.
详解:∵∠BAC=90°,∠DAE=90°,
∴∠BAD+∠DAC=∠DAC+∠CAE=90°,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),∴CE=BD.
故填CE=BD.
【构建模型】过点A作AF⊥AE,交BE于点F,如图.
∵BC为☉O的直径,∴∠BAC=90°.
∵AB=AC,∴∠ABC=∠ACB=45°.
∵∠AEB=∠ACB,∴∠AEB=45°.
∵AF⊥AE,∴∠AFE=45°.∴AF=AE=EF.
∵∠BAC=∠FAE=90°,
即∠BAF+∠FAC=∠FAC+∠CAE=90°,
∴∠BAF=∠CAE.
在△BAF和△CAE中,,
∴△BAF≌△CAE(SAS).
∴BF=CE=3.∴EF=BE-BF=9-3=6.
∴AE=3.
【运用模型】在BE上取一点F,使AF=AE,如图.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°.
∵∠AEB=∠ACB,∴∠AEB=60°.
∴△AEF为等边三角形.∴∠FAE=60°,AE=EF.
∴∠BAF+∠FAC=∠FAC+∠CAE=60°.
∴∠BAF=∠CAE.
在△BAF和△CAE中,,
∴△BAF≌△CAE(SAS).
∴BF=CE=6.∴EF=BE-BF=10-6=4.
∴AE=EF=4.
2.解析【感知】45.
【探究】补充证明过程如下:
∴PB=EB,∠PBC=∠EBA,
∴∠EBA+∠ABP=∠PBC+∠ABP=∠ABC=60°,
∴△PBE是等边三角形,
∴PB=PE=PA+AE=PA+PC.
【应用】.
详解:如图,延长PA至点E,使AE=PC,连接BE.
∵四边形ABCP是☉O的内接四边形,
∴∠BAP+∠BCP=180°.
又∵∠BAP+∠BAE=180°,∴∠BCP=∠BAE.
又∵PC=EA,BC=BA,∴△PBC≌△EBA(SAS),
∴PB=EB,∠PBC=∠EBA,
∴∠EBA+∠ABP=∠PBC+∠ABP=∠ABC=90°,
∴PE=PB.∵PE=PA+AE=PA+PC,
∴PA+PC=PB,又∵PB=2PA,
∴PA+PC=×2PA=4PA,
∴PC=3PA,∴==.
3.解析(1)如图①,连接OP,OM,过点O作OM'⊥AB,垂足为M',则OP+PM≥OM≥OM'.
图①
∵☉O的半径为4,∴PM≥OM-4≥OM'-4.
∵OA=OB,∠AOB=120°,∴∠A=30°,AM'=AB=12.
∴OM'=AM'·tan 30°=12×tan 30°=4.
∴PM≥OM'-4=4-4,
∴线段PM长度的最小值为4-4.
(2)如图②,分别在BC,AE上截取BB'=AA'=30 m.
连接A'B',B'O、OP、OE、B'E.
图②
∵OM⊥AB,BB'⊥AB,∴OM∥BB'.又ON=BB',
∴四边形BB'ON是平行四边形.∴BN=B'O.
∵B'O+OP+PE≥B'O+OE≥B'E,
∴BN+PE≥B'E-OP.
∴当点O在B'E上时,BN+PE取得最小值.
作☉O',使圆心O'在B'E上,半径=30 m,
作O'M'⊥AB,垂足为M',与☉O'交于点N',与A'B'交于点H.
易证△B'O'H∽△B'EA',∴=.
∵☉O'在矩形AFDE区域内(含边界),
∴当☉O'与FD相切时,B'H最短,即B'H=10 000-6 000+30=4 030(m),
此时O'H也最短,∵M'N'=O'H,∴M'N'也最短.
O'H===4 017.91(m).
∴O'M'=O'H+M'H=4 047.91(m).
∴此时环道☉O的圆心O到AB的距离为4 047.91 m.
4.解析(1)证明:∵CF⊥OE,OC是半径,∴CF与☉O相切.又∵BE与☉O相切,
∴BF=CF,∴EF=2BF=2CF,∴sin E==,∴∠E=30°,∴∠EOB=60°.
连接OD(图略),则OD=OB.又∵CD=CB,∴OC垂直平分BD,∴∠ABD=90°-60°=30°,
∴∠ABD=∠E.∵AB是直径,∴∠ADB=90°=∠EBO,
在Rt△ABD中,∠ABD=30°,∴AD=AB=BO,∴△ADB≌△OBE.
(2)MN=BM+DN.
证明:延长ND至H,使得DH=BM,连接CH,BD,如图所示.
∵∠CBM+∠NDC=180°,∠HDC+∠NDC=180°,∴∠HDC=∠CBM.
又∵CD=CB,DH=BM,∴△HCD≌△MCB,∴∠BCM=∠DCH,CM=CH.
由(1)可得∠ABD=30°,∠ADB=90°,∴∠A=60°,∴∠DCB=180°-∠A=120°.
∵∠MCN=60°,∴∠BCM+∠NCD=60°,∴∠NCH=∠DCH+∠NCD=60°=∠NCM.
又∵NC=NC,CM=CH,∴△CNH≌△CNM,∴NH=MN,∴MN=DH+DN=BM+DN.
方法解读 截长补短法:
①截长法:在长线段上截取一条线段,使其等于其中一条短线段,然后证明剩下的线段等于另一条短线段.②补短法:延长短线段,使其延长部分等于另一条短线段,然后证明延长后的线段等于长线段(或延长短线段,使延长后的线段等于长线段,然后证明延长部分等于另一条短线段).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
圆
专项素养综合全练(五) 圆的综合探究题
类型一 圆性质的综合探究题
1.(2023山东威海文登期末)
【初识模型】如图1,在△ABC中,AB=AC,∠BAC=90°.点D为BC边上一点,以AD为边作△ADE,使∠DAE=90°,AE=AD,连接CE,则CE与BD的数量关系是 .
【构建模型】如图2,△ABC内接于☉O,BC为☉O的直径,AB=AC,点E为弧AC上一点,连接AE,BE,CE.若CE=3,BE=9,求AE的长.
【运用模型】如图3,等边△ABC内接于☉O,点E为弧AC上一点,连接AE,BE,CE.若CE=6,BE=10,求AE的长.
图1
图2
图3
2.【新考向·过程性学习试题】(2023吉林长春中考)【感知】如图①,点A、B、P均在☉O上,∠AOB=90°,则锐角∠APB的大小为 度.
【探究】小明遇到这样一个问题:如图②,☉O是等边三角形ABC的外接圆,点P在上(点P不与点A、C重合),连接PA、PB、PC.求证:PB=PA+PC.
小明发现,延长PA至点E,使AE=PC,连接BE,通过证明△PBC≌△EBA可推得△PBE是等边三角形,进而得证.下面是小明的部分证明过程:
证明:延长PA至点E,使AE=PC,连接BE.
∵四边形ABCP是☉O的内接四边形,
∴∠BAP+∠BCP=180°,
∵∠BAP+∠BAE=180°,
∴∠BCP=∠BAE,
∵△ABC是等边三角形,
∴BA=BC,
∴△PBC≌△EBA(SAS).
请你补全余下的证明过程.
【应用】如图③,☉O是△ABC的外接圆,∠ABC=90°,AB=BC,点P在☉O上,且点P与点B在AC的两侧,连接PA、PB、PC,若PB=2PA,则的值为 .
图①
图②
图③
类型二 圆位置关系的综合探究题
3.(2023陕西中考A卷)(1)如图①,在△OAB中,OA=OB,∠AOB=120°,AB=24.若☉O的半径为4,点P在☉O上,点M在AB上,连接PM,求线段PM长度的最小值.
(2)如图②,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的一个交通枢纽,已知:∠A=∠ABC=∠AED=90°,AB=AE=10 000 m,BC=DE=
6 000 m,根据新区的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修一个半径为30 m的圆形环道☉O,过圆心O,作OM⊥AB,垂足为M,与☉O交于点N,连接BN,点P在☉O上,连接EP,其中,线段BN、EP及MN是要修的三条道路,要在所修道路BN、EP长度之和最小的情况下,使所修道路MN最短,试求此时环道☉O的圆心O到AB的距离(即OM的长).
4.【截长补短法】(2023山东济宁中考)如图,已知AB是☉O的直径,CD=CB,BE切☉O于点B,过点C作CF⊥OE,交BE于点F,若EF=2BF.
(1)如图1,连接BD,求证:△ADB≌△OBE;
(2)如图2,N是AD上一点,在AB上取一点M,使∠MCN=60°,连接MN.请问:三条线段MN,BM,DN有怎样的数量关系 并证明你的结论.
图1
图2
答案全解全析
1.解析【初识模型】CE=BD.
详解:∵∠BAC=90°,∠DAE=90°,
∴∠BAD+∠DAC=∠DAC+∠CAE=90°,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),∴CE=BD.
故填CE=BD.
【构建模型】过点A作AF⊥AE,交BE于点F,如图.
∵BC为☉O的直径,∴∠BAC=90°.
∵AB=AC,∴∠ABC=∠ACB=45°.
∵∠AEB=∠ACB,∴∠AEB=45°.
∵AF⊥AE,∴∠AFE=45°.∴AF=AE=EF.
∵∠BAC=∠FAE=90°,
即∠BAF+∠FAC=∠FAC+∠CAE=90°,
∴∠BAF=∠CAE.
在△BAF和△CAE中,,
∴△BAF≌△CAE(SAS).
∴BF=CE=3.∴EF=BE-BF=9-3=6.
∴AE=3.
【运用模型】在BE上取一点F,使AF=AE,如图.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°.
∵∠AEB=∠ACB,∴∠AEB=60°.
∴△AEF为等边三角形.∴∠FAE=60°,AE=EF.
∴∠BAF+∠FAC=∠FAC+∠CAE=60°.
∴∠BAF=∠CAE.
在△BAF和△CAE中,,
∴△BAF≌△CAE(SAS).
∴BF=CE=6.∴EF=BE-BF=10-6=4.
∴AE=EF=4.
2.解析【感知】45.
【探究】补充证明过程如下:
∴PB=EB,∠PBC=∠EBA,
∴∠EBA+∠ABP=∠PBC+∠ABP=∠ABC=60°,
∴△PBE是等边三角形,
∴PB=PE=PA+AE=PA+PC.
【应用】.
详解:如图,延长PA至点E,使AE=PC,连接BE.
∵四边形ABCP是☉O的内接四边形,
∴∠BAP+∠BCP=180°.
又∵∠BAP+∠BAE=180°,∴∠BCP=∠BAE.
又∵PC=EA,BC=BA,∴△PBC≌△EBA(SAS),
∴PB=EB,∠PBC=∠EBA,
∴∠EBA+∠ABP=∠PBC+∠ABP=∠ABC=90°,
∴PE=PB.∵PE=PA+AE=PA+PC,
∴PA+PC=PB,又∵PB=2PA,
∴PA+PC=×2PA=4PA,
∴PC=3PA,∴==.
3.解析(1)如图①,连接OP,OM,过点O作OM'⊥AB,垂足为M',则OP+PM≥OM≥OM'.
图①
∵☉O的半径为4,∴PM≥OM-4≥OM'-4.
∵OA=OB,∠AOB=120°,∴∠A=30°,AM'=AB=12.
∴OM'=AM'·tan 30°=12×tan 30°=4.
∴PM≥OM'-4=4-4,
∴线段PM长度的最小值为4-4.
(2)如图②,分别在BC,AE上截取BB'=AA'=30 m.
连接A'B',B'O、OP、OE、B'E.
图②
∵OM⊥AB,BB'⊥AB,∴OM∥BB'.又ON=BB',
∴四边形BB'ON是平行四边形.∴BN=B'O.
∵B'O+OP+PE≥B'O+OE≥B'E,
∴BN+PE≥B'E-OP.
∴当点O在B'E上时,BN+PE取得最小值.
作☉O',使圆心O'在B'E上,半径=30 m,
作O'M'⊥AB,垂足为M',与☉O'交于点N',与A'B'交于点H.
易证△B'O'H∽△B'EA',∴=.
∵☉O'在矩形AFDE区域内(含边界),
∴当☉O'与FD相切时,B'H最短,即B'H=10 000-6 000+30=4 030(m),
此时O'H也最短,∵M'N'=O'H,∴M'N'也最短.
O'H===4 017.91(m).
∴O'M'=O'H+M'H=4 047.91(m).
∴此时环道☉O的圆心O到AB的距离为4 047.91 m.
4.解析(1)证明:∵CF⊥OE,OC是半径,∴CF与☉O相切.又∵BE与☉O相切,
∴BF=CF,∴EF=2BF=2CF,∴sin E==,∴∠E=30°,∴∠EOB=60°.
连接OD(图略),则OD=OB.又∵CD=CB,∴OC垂直平分BD,∴∠ABD=90°-60°=30°,
∴∠ABD=∠E.∵AB是直径,∴∠ADB=90°=∠EBO,
在Rt△ABD中,∠ABD=30°,∴AD=AB=BO,∴△ADB≌△OBE.
(2)MN=BM+DN.
证明:延长ND至H,使得DH=BM,连接CH,BD,如图所示.
∵∠CBM+∠NDC=180°,∠HDC+∠NDC=180°,∴∠HDC=∠CBM.
又∵CD=CB,DH=BM,∴△HCD≌△MCB,∴∠BCM=∠DCH,CM=CH.
由(1)可得∠ABD=30°,∠ADB=90°,∴∠A=60°,∴∠DCB=180°-∠A=120°.
∵∠MCN=60°,∴∠BCM+∠NCD=60°,∴∠NCH=∠DCH+∠NCD=60°=∠NCM.
又∵NC=NC,CM=CH,∴△CNH≌△CNM,∴NH=MN,∴MN=DH+DN=BM+DN.
方法解读 截长补短法:
①截长法:在长线段上截取一条线段,使其等于其中一条短线段,然后证明剩下的线段等于另一条短线段.②补短法:延长短线段,使其延长部分等于另一条短线段,然后证明延长后的线段等于长线段(或延长短线段,使延长后的线段等于长线段,然后证明延长部分等于另一条短线段).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
