方程的根与函数零点
图片预览




文档简介
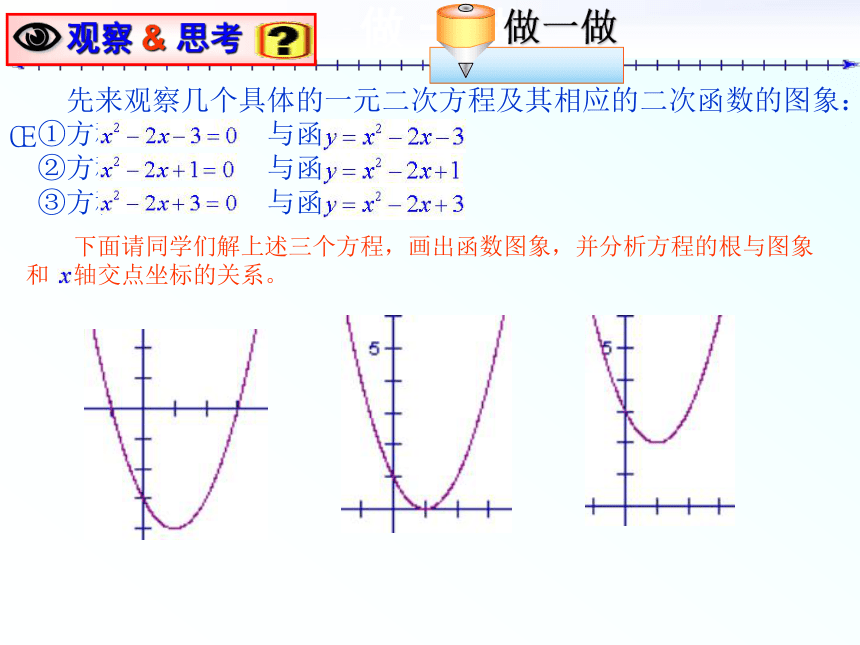
课件12张PPT。方程的根与函数的零点 做 一 做 先来观察几个具体的一元二次方程及其相应的二次函数的图象:
?①方程 与函数 ?②方程 与函数 ?③方程 与函数 下面请同学们解上述三个方程,画出函数图象,并分析方程的根与图象和 轴交点坐标的关系。
函数的零点定义:
对于函数 ,我们把使 的实数 叫做函数的零点。
函数零点与方程根的联系:
函数 的零点就是方程 的实数根,也就是函数 的图像与 轴的交点的横坐标。
即:
方程 有实数根
函数 的图像与 轴有交点
函数 有零点二次函数的零点:
二次函数
(1)?>0,方程 有两个不相等的实数根,二次函数图像与 轴有两个交点,二次函数有两个零点。
(2)?=0,方程 有两个相等的实数根,二次函数图像与 轴有一个交点,二次函数有一个零点。
(3)?<0,方程 无实数根,二次函数图像与 轴没有交点,二次函数没有零点。
你能想到吗?练习 通过以上的学习,你知道怎么求函数的零点了吗?练习:求下列函数的零点:
(1)
(2)
(3)
函数零点的求法:
(1)求方程 的实数根。
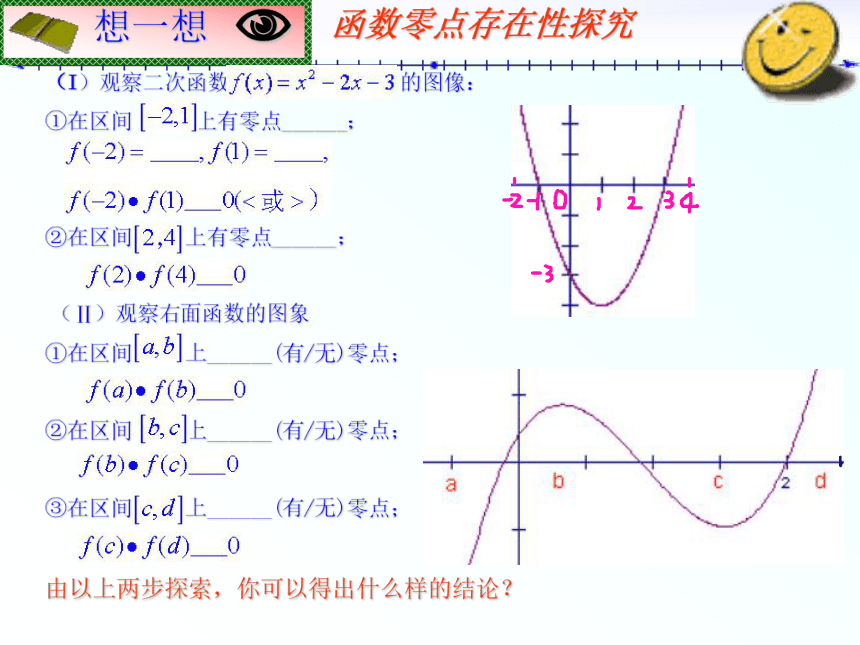
(2)对于不能用公式法求根的方程 来说,我们可以将它与函数 联系起来,利用函数的性质找出零点。想一想(I)观察二次函数 的图像:
①在区间 上有零点______;
②在区间 上有零点______;
(Ⅱ)观察右面函数的图象
①在区间 上______(有/无)零点;
②在区间 上______(有/无)零点;
③在区间 上______(有/无)零点;
由以上两步探索,你可以得出什么样的结论?函数零点存在性探究 如果函数 在区间 上的图像是连续不断的一条曲线,并且有 ,那么,函数 在区间 内有零点,即存在 ,使得 ,这个 也就是方程 的根。总结一下要好好理解上面的结论啊!!!例题学一学例1 求函数 的零点的个数。
解:先作出 、 的对应值表和图像:
由表可知, 则 ,这说明函数 在区间 内有零点。由于函数 在定义域 内是增函数,所以它仅有一个零点。动手做做吧!随堂练习1 利用函数图像判断下列方程有没有根,有几个根?2 作出下列函数的图像,并指出下列函数零点所在的大致区间。P97本节课你的收获是什么?小结本节课你学到了什么?本节课所学知识内容有哪些? 判定函数在某个区间存在零点的基本步骤是什么? 不太明白的地方,请向老师提出 。作业 作业1、预习:教材p98 3.1.2用二分法求方程的近似解 .
2、课堂作业:习题3.1 第2题.谢谢!
函数的零点定义:
对于函数 ,我们把使 的实数 叫做函数的零点。
函数零点与方程根的联系:
函数 的零点就是方程 的实数根,也就是函数 的图像与 轴的交点的横坐标。
即:
方程 有实数根
函数 的图像与 轴有交点
函数 有零点二次函数的零点:
二次函数
(1)?>0,方程 有两个不相等的实数根,二次函数图像与 轴有两个交点,二次函数有两个零点。
(2)?=0,方程 有两个相等的实数根,二次函数图像与 轴有一个交点,二次函数有一个零点。
(3)?<0,方程 无实数根,二次函数图像与 轴没有交点,二次函数没有零点。
你能想到吗?练习 通过以上的学习,你知道怎么求函数的零点了吗?练习:求下列函数的零点:
(1)
(2)
(3)
函数零点的求法:
(1)求方程 的实数根。
(2)对于不能用公式法求根的方程 来说,我们可以将它与函数 联系起来,利用函数的性质找出零点。想一想(I)观察二次函数 的图像:
①在区间 上有零点______;
②在区间 上有零点______;
(Ⅱ)观察右面函数的图象
①在区间 上______(有/无)零点;
②在区间 上______(有/无)零点;
③在区间 上______(有/无)零点;
由以上两步探索,你可以得出什么样的结论?函数零点存在性探究 如果函数 在区间 上的图像是连续不断的一条曲线,并且有 ,那么,函数 在区间 内有零点,即存在 ,使得 ,这个 也就是方程 的根。总结一下要好好理解上面的结论啊!!!例题学一学例1 求函数 的零点的个数。
解:先作出 、 的对应值表和图像:
由表可知, 则 ,这说明函数 在区间 内有零点。由于函数 在定义域 内是增函数,所以它仅有一个零点。动手做做吧!随堂练习1 利用函数图像判断下列方程有没有根,有几个根?2 作出下列函数的图像,并指出下列函数零点所在的大致区间。P97本节课你的收获是什么?小结本节课你学到了什么?本节课所学知识内容有哪些? 判定函数在某个区间存在零点的基本步骤是什么? 不太明白的地方,请向老师提出 。作业 作业1、预习:教材p98 3.1.2用二分法求方程的近似解 .
2、课堂作业:习题3.1 第2题.谢谢!
