5.2 圆的对称性课时练(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
第五章 圆
2 圆的对称性
基础过关全练
知识点1 圆的对称性
1.(2022贵州毕节金沙一模)下列说法中,不正确的是 ( )
A.圆既是轴对称图形又是中心对称图形
B.圆有无数条对称轴
C.圆的每一条直径都是它的对称轴
D.圆的对称中心是它的圆心
2.【新独家原创】如图所示的图案中,若圆的半径为2,则阴影部分的面积为 .
知识点2 圆的有关概念——弦与弧
3.(2023山东临沂郯城期末改编)有下列四种说法:
①长度相等的弧是等弧;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中,错误的说法有( )
A.1种 B.2种 C.3种 D.4种
4.(2021安徽安庆桐城期末)已知AB是☉O的弦,☉O的半径为r,下列关系式一定成立的是( )
A.AB>r B.AB知识点3 圆心角、弧、弦之间的关系
5.在同圆或等圆中,如果圆心角∠BOA等于另一圆心角∠COD的2倍,则下列式子中,一定成立的是( )
A.AB=2CD B.l=2l
C.l<2l D.l=l
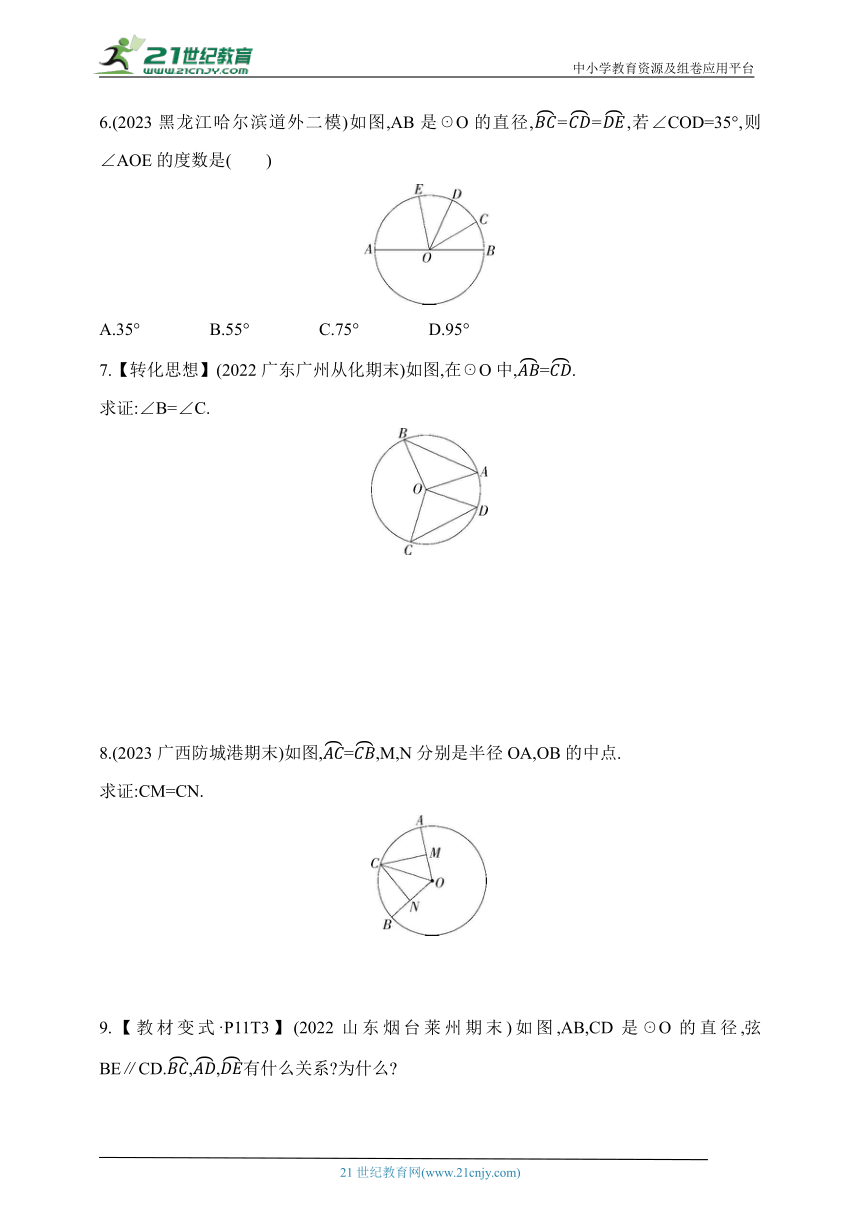
6.(2023黑龙江哈尔滨道外二模)如图,AB是☉O的直径,==,若∠COD=35°,则∠AOE的度数是( )
A.35° B.55° C.75° D.95°
7.【转化思想】(2022广东广州从化期末)如图,在☉O中,=.
求证:∠B=∠C.
8.(2023广西防城港期末)如图,=,M,N分别是半径OA,OB的中点.
求证:CM=CN.
9.【教材变式·P11T3】(2022山东烟台莱州期末)如图,AB,CD是☉O的直径,弦BE∥CD.,,有什么关系 为什么
知识点4 弧的度数
10.下列命题是真命题的是 .(填序号)
①度数相等的弧所对的圆心角相等;
②相等的圆心角所对的两条弦相等;
③直径所对的弧是180°;
④长度相等的弧的度数相等.
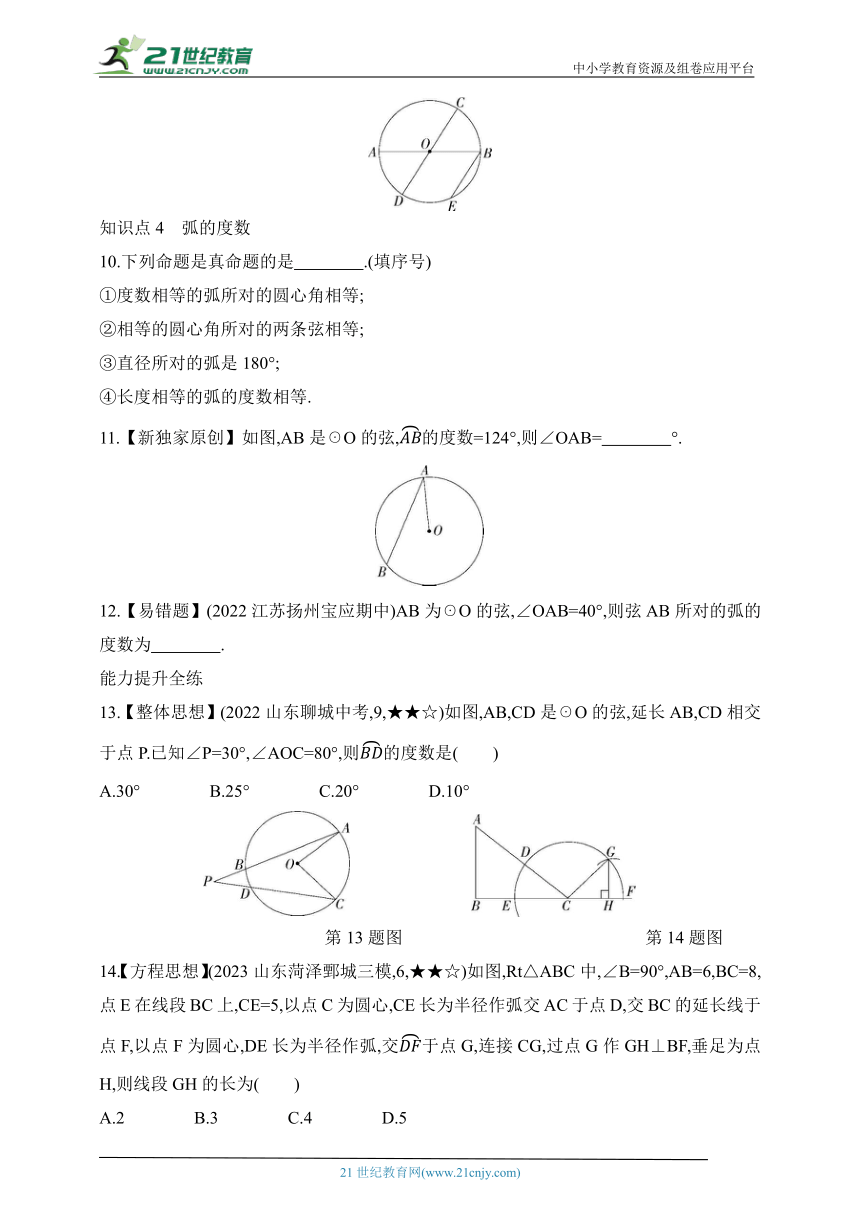
11.【新独家原创】如图,AB是☉O的弦,的度数=124°,则∠OAB= °.
12.【易错题】(2022江苏扬州宝应期中)AB为☉O的弦,∠OAB=40°,则弦AB所对的弧的度数为 .
能力提升全练
13.【整体思想】(2022山东聊城中考,9,★★☆)如图,AB,CD是☉O的弦,延长AB,CD相交于点P.已知∠P=30°,∠AOC=80°,则的度数是( )
A.30° B.25° C.20° D.10°
第13题图 第14题图
14.【方程思想】(2023山东菏泽鄄城三模,6,★★☆)如图,Rt△ABC中,∠B=90°,AB=6,BC=8,点E在线段BC上,CE=5,以点C为圆心,CE长为半径作弧交AC于点D,交BC的延长线于点F,以点F为圆心,DE长为半径作弧,交于点G,连接CG,过点G作GH⊥BF,垂足为点H,则线段GH的长为( )
A.2 B.3 C.4 D.5
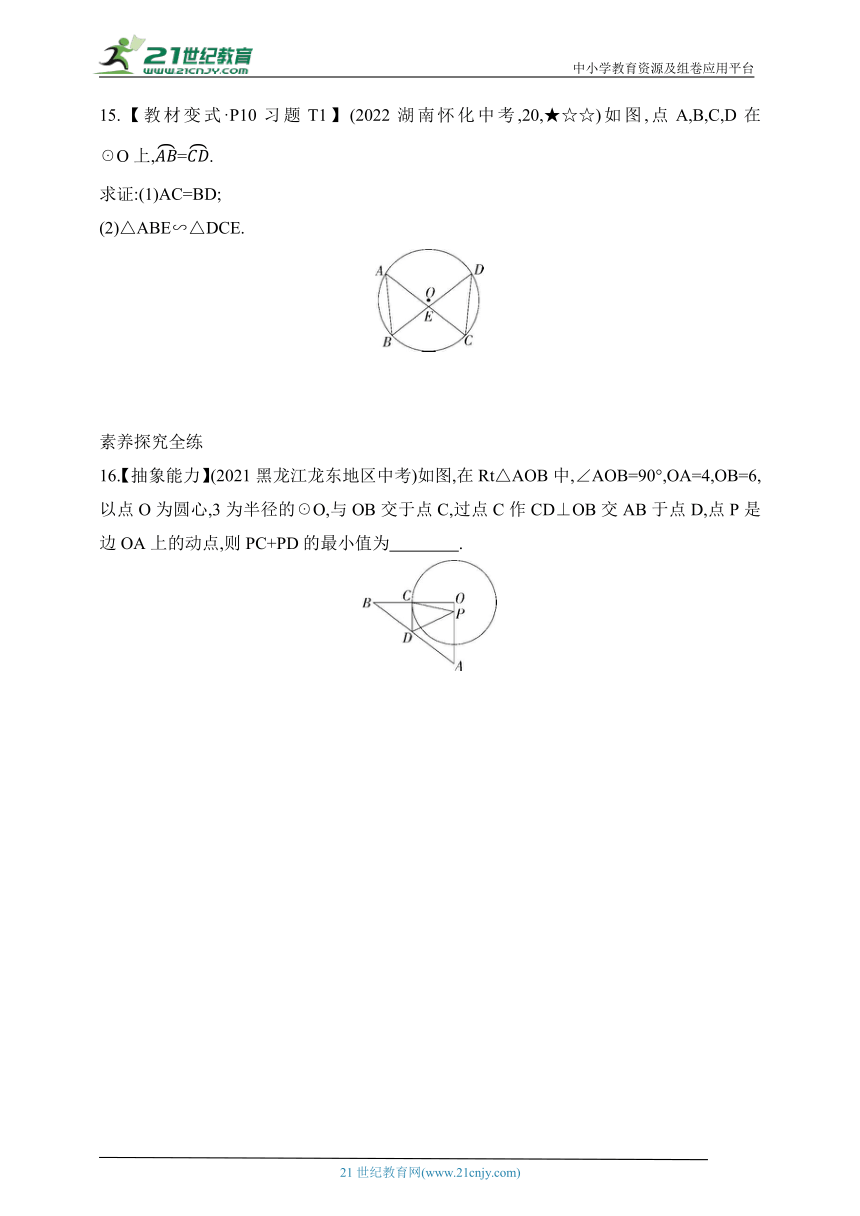
15.【教材变式·P10习题T1】(2022湖南怀化中考,20,★☆☆)如图,点A,B,C,D在☉O上,=.
求证:(1)AC=BD;
(2)△ABE∽△DCE.
素养探究全练
16.【抽象能力】(2021黑龙江龙东地区中考)如图,在Rt△AOB中,∠AOB=90°,OA=4,OB=6,以点O为圆心,3为半径的☉O,与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点,则PC+PD的最小值为 .
第五章 圆
2 圆的对称性
答案全解全析
基础过关全练
1.C A项,圆既是轴对称图形又是中心对称图形,说法正确;B项,圆有无数条对称轴,说法正确;C项,圆的每一条直径所在直线都是它的对称轴,说法错误;D项,圆的对称中心是它的圆心,说法正确.故选C.
2.答案π
解析由圆和正方形的旋转对称性,可知三个小阴影部分若集中到一起,则其面积为圆面积的,所以阴影部分的面积为=π.
3.B ①在同圆或等圆中,能够重合的两条弧叫做等弧,故此说法错误;②直径是弦,且是圆内最长的弦,故此说法正确;③只有过圆心的弦才是直径,故此说法错误;④半圆是弧,但弧不一定是半圆,故此说法正确.所以错误的说法是①③.故选B.
4.D 若AB是☉O的直径,则AB=2r;若AB不是☉O的直径,则AB<2r,∴AB≤2r,故选D.
5.B 如图,作∠AOB的平分线,交☉O于E,连接AE,BE,AB,CD.
∵OE平分∠AOB,∴∠AOE=∠BOE.
又∵∠AOB=2∠COD,∴∠AOE=∠BOE=∠COD.
∴AE=BE=CD,==.∴=2.
在△ABE中,AE+BE>AB,∴AB<2CD.故选B.
6.C ∵==,∠COD=35°,
∴∠BOC=∠EOD=∠COD=35°.
∴∠AOE=180°-∠EOD-∠COD-∠BOC=75°.故选C.
7.证明 ∵在☉O中,=,∴∠AOB=∠COD.
∵OA=OB,OC=OD,∴∠A=∠B,∠C=∠D,
∴∠B=,∠C=.
∴∠B=∠C.
8.证明 在☉O中,∵=,∴∠AOC=∠BOC.
∵OA=OB,M,N分别是半径OA,OB的中点,
∴OM=ON.∴△COM≌△CON(SAS).∴CM=CN.
9.解析==.理由:连接OE(图略).
∵∠BOC=∠AOD,∴=.
∵BE∥CD,∴∠BOC=∠B,∠DOE=∠E.
∵OB=OE,∴∠B=∠E.∴∠BOC=∠DOE.
∴=.∴==.
10.答案①③
解析①度数相等的弧所对的圆心角相等,原命题是真命题;②在同圆或等圆中,相等的圆心角所对的两条弦相等,原命题是假命题;③直径所对的弧是半圆,半圆的度数为180°,原命题是真命题;④在同圆或等圆中,长度相等的弧的度数相等,原命题是假命题.故填①③.
11.答案28
解析连接OB(图略).
∵的度数=124°,∴∠AOB=124°.
∵OA=OB,∴∠OAB=∠OBA==28°.
12.答案100°或260°
解析如图,连接OB.
∵OA=OB,∴∠OAB=∠OBA=40°.
∴∠AOB=180°-40°-40°=100°.
∴弦AB所对的弧的度数为100°或260°.
能力提升全练
13.C 如图,连接AC、OB、OD,
∵∠AOC=80°,∴∠OAC+∠OCA=100°.
∵∠P=30°,∴∠PAC+∠PCA=150°.
∴∠PAO+∠PCO=50°.∵OA=OB,OC=OD,
∴∠OBA=∠OAB,∠OCD=∠ODC.
∴∠OBA+∠ODC=50°.∴∠BOA+∠COD=260°.
∴∠BOD=360°-80°-260°=20°.
∴的度数为20°.故选C.
14.B 连接GF,DE(图略).∵以点F为圆心,DE长为半径作弧,交于点G,
∴FG=DE.∴=.∴∠GCH=∠ACB.∵GH⊥BF,∴∠GHC=90°.
∴∠B=∠GHC=90°.∴△CGH∽△CAB.∴GH∶AB=CG∶AC.
∵AC===10,
∴GH∶6=5∶10,∴GH=3.故选B.
15.证明 (1)∵=,∴+=+,即=.∴AC=BD.
(2)连接AD(图略).∵=,∴AB=CD.
又BD=AC,AD=DA,∴△ABD≌△DCA.
∴∠B=∠C.又∠AEB=∠DEC,∴△ABE∽△DCE.
素养探究全练
16.答案2
解析如图,延长CO交☉O于点E,连接ED,交AO于点P,此时PC+PD的值最小,最小值为线段DE的长.
∵CD⊥OB,∴∠DCB=90°.∵∠AOB=90°,∴∠DCB=∠AOB.∵∠B=∠B,
∴△BCD∽△BOA,∴=,即=,解得CD=2.
在Rt△CDE中,DE===2,
即PC+PD的最小值为2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
第五章 圆
2 圆的对称性
基础过关全练
知识点1 圆的对称性
1.(2022贵州毕节金沙一模)下列说法中,不正确的是 ( )
A.圆既是轴对称图形又是中心对称图形
B.圆有无数条对称轴
C.圆的每一条直径都是它的对称轴
D.圆的对称中心是它的圆心
2.【新独家原创】如图所示的图案中,若圆的半径为2,则阴影部分的面积为 .
知识点2 圆的有关概念——弦与弧
3.(2023山东临沂郯城期末改编)有下列四种说法:
①长度相等的弧是等弧;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中,错误的说法有( )
A.1种 B.2种 C.3种 D.4种
4.(2021安徽安庆桐城期末)已知AB是☉O的弦,☉O的半径为r,下列关系式一定成立的是( )
A.AB>r B.AB
5.在同圆或等圆中,如果圆心角∠BOA等于另一圆心角∠COD的2倍,则下列式子中,一定成立的是( )
A.AB=2CD B.l=2l
C.l<2l D.l=l
6.(2023黑龙江哈尔滨道外二模)如图,AB是☉O的直径,==,若∠COD=35°,则∠AOE的度数是( )
A.35° B.55° C.75° D.95°
7.【转化思想】(2022广东广州从化期末)如图,在☉O中,=.
求证:∠B=∠C.
8.(2023广西防城港期末)如图,=,M,N分别是半径OA,OB的中点.
求证:CM=CN.
9.【教材变式·P11T3】(2022山东烟台莱州期末)如图,AB,CD是☉O的直径,弦BE∥CD.,,有什么关系 为什么
知识点4 弧的度数
10.下列命题是真命题的是 .(填序号)
①度数相等的弧所对的圆心角相等;
②相等的圆心角所对的两条弦相等;
③直径所对的弧是180°;
④长度相等的弧的度数相等.
11.【新独家原创】如图,AB是☉O的弦,的度数=124°,则∠OAB= °.
12.【易错题】(2022江苏扬州宝应期中)AB为☉O的弦,∠OAB=40°,则弦AB所对的弧的度数为 .
能力提升全练
13.【整体思想】(2022山东聊城中考,9,★★☆)如图,AB,CD是☉O的弦,延长AB,CD相交于点P.已知∠P=30°,∠AOC=80°,则的度数是( )
A.30° B.25° C.20° D.10°
第13题图 第14题图
14.【方程思想】(2023山东菏泽鄄城三模,6,★★☆)如图,Rt△ABC中,∠B=90°,AB=6,BC=8,点E在线段BC上,CE=5,以点C为圆心,CE长为半径作弧交AC于点D,交BC的延长线于点F,以点F为圆心,DE长为半径作弧,交于点G,连接CG,过点G作GH⊥BF,垂足为点H,则线段GH的长为( )
A.2 B.3 C.4 D.5
15.【教材变式·P10习题T1】(2022湖南怀化中考,20,★☆☆)如图,点A,B,C,D在☉O上,=.
求证:(1)AC=BD;
(2)△ABE∽△DCE.
素养探究全练
16.【抽象能力】(2021黑龙江龙东地区中考)如图,在Rt△AOB中,∠AOB=90°,OA=4,OB=6,以点O为圆心,3为半径的☉O,与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点,则PC+PD的最小值为 .
第五章 圆
2 圆的对称性
答案全解全析
基础过关全练
1.C A项,圆既是轴对称图形又是中心对称图形,说法正确;B项,圆有无数条对称轴,说法正确;C项,圆的每一条直径所在直线都是它的对称轴,说法错误;D项,圆的对称中心是它的圆心,说法正确.故选C.
2.答案π
解析由圆和正方形的旋转对称性,可知三个小阴影部分若集中到一起,则其面积为圆面积的,所以阴影部分的面积为=π.
3.B ①在同圆或等圆中,能够重合的两条弧叫做等弧,故此说法错误;②直径是弦,且是圆内最长的弦,故此说法正确;③只有过圆心的弦才是直径,故此说法错误;④半圆是弧,但弧不一定是半圆,故此说法正确.所以错误的说法是①③.故选B.
4.D 若AB是☉O的直径,则AB=2r;若AB不是☉O的直径,则AB<2r,∴AB≤2r,故选D.
5.B 如图,作∠AOB的平分线,交☉O于E,连接AE,BE,AB,CD.
∵OE平分∠AOB,∴∠AOE=∠BOE.
又∵∠AOB=2∠COD,∴∠AOE=∠BOE=∠COD.
∴AE=BE=CD,==.∴=2.
在△ABE中,AE+BE>AB,∴AB<2CD.故选B.
6.C ∵==,∠COD=35°,
∴∠BOC=∠EOD=∠COD=35°.
∴∠AOE=180°-∠EOD-∠COD-∠BOC=75°.故选C.
7.证明 ∵在☉O中,=,∴∠AOB=∠COD.
∵OA=OB,OC=OD,∴∠A=∠B,∠C=∠D,
∴∠B=,∠C=.
∴∠B=∠C.
8.证明 在☉O中,∵=,∴∠AOC=∠BOC.
∵OA=OB,M,N分别是半径OA,OB的中点,
∴OM=ON.∴△COM≌△CON(SAS).∴CM=CN.
9.解析==.理由:连接OE(图略).
∵∠BOC=∠AOD,∴=.
∵BE∥CD,∴∠BOC=∠B,∠DOE=∠E.
∵OB=OE,∴∠B=∠E.∴∠BOC=∠DOE.
∴=.∴==.
10.答案①③
解析①度数相等的弧所对的圆心角相等,原命题是真命题;②在同圆或等圆中,相等的圆心角所对的两条弦相等,原命题是假命题;③直径所对的弧是半圆,半圆的度数为180°,原命题是真命题;④在同圆或等圆中,长度相等的弧的度数相等,原命题是假命题.故填①③.
11.答案28
解析连接OB(图略).
∵的度数=124°,∴∠AOB=124°.
∵OA=OB,∴∠OAB=∠OBA==28°.
12.答案100°或260°
解析如图,连接OB.
∵OA=OB,∴∠OAB=∠OBA=40°.
∴∠AOB=180°-40°-40°=100°.
∴弦AB所对的弧的度数为100°或260°.
能力提升全练
13.C 如图,连接AC、OB、OD,
∵∠AOC=80°,∴∠OAC+∠OCA=100°.
∵∠P=30°,∴∠PAC+∠PCA=150°.
∴∠PAO+∠PCO=50°.∵OA=OB,OC=OD,
∴∠OBA=∠OAB,∠OCD=∠ODC.
∴∠OBA+∠ODC=50°.∴∠BOA+∠COD=260°.
∴∠BOD=360°-80°-260°=20°.
∴的度数为20°.故选C.
14.B 连接GF,DE(图略).∵以点F为圆心,DE长为半径作弧,交于点G,
∴FG=DE.∴=.∴∠GCH=∠ACB.∵GH⊥BF,∴∠GHC=90°.
∴∠B=∠GHC=90°.∴△CGH∽△CAB.∴GH∶AB=CG∶AC.
∵AC===10,
∴GH∶6=5∶10,∴GH=3.故选B.
15.证明 (1)∵=,∴+=+,即=.∴AC=BD.
(2)连接AD(图略).∵=,∴AB=CD.
又BD=AC,AD=DA,∴△ABD≌△DCA.
∴∠B=∠C.又∠AEB=∠DEC,∴△ABE∽△DCE.
素养探究全练
16.答案2
解析如图,延长CO交☉O于点E,连接ED,交AO于点P,此时PC+PD的值最小,最小值为线段DE的长.
∵CD⊥OB,∴∠DCB=90°.∵∠AOB=90°,∴∠DCB=∠AOB.∵∠B=∠B,
∴△BCD∽△BOA,∴=,即=,解得CD=2.
在Rt△CDE中,DE===2,
即PC+PD的最小值为2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
