5.4.1 圆周角定理及其推论1、2课时练(含解析)
文档属性
| 名称 | 5.4.1 圆周角定理及其推论1、2课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 451.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:30:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
第五章 圆
4 圆周角和圆心角的关系
第1课时 圆周角定理及其推论1、2
基础过关全练
知识点1 圆周角
1.(2021河南开封期末)下列图形中的角是圆周角的是( )
A B C D
知识点2 圆周角定理
2.(2023河南中考)如图,点A,B,C在☉O上,若∠C=55°,则∠AOB的度数为( )
A.95° B.100° C.105° D.110°
3.(2022贵州铜仁中考)如图,OA,OB是☉O的两条半径,点C在☉O上,若∠AOB=80°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
4.【构造法】(2023四川广安中考)如图,△ABC的三个顶点在☉O上,圆的半径为7,∠BAC=60°,则弦BC的长度为 .
知识点3 圆周角定理的推论1
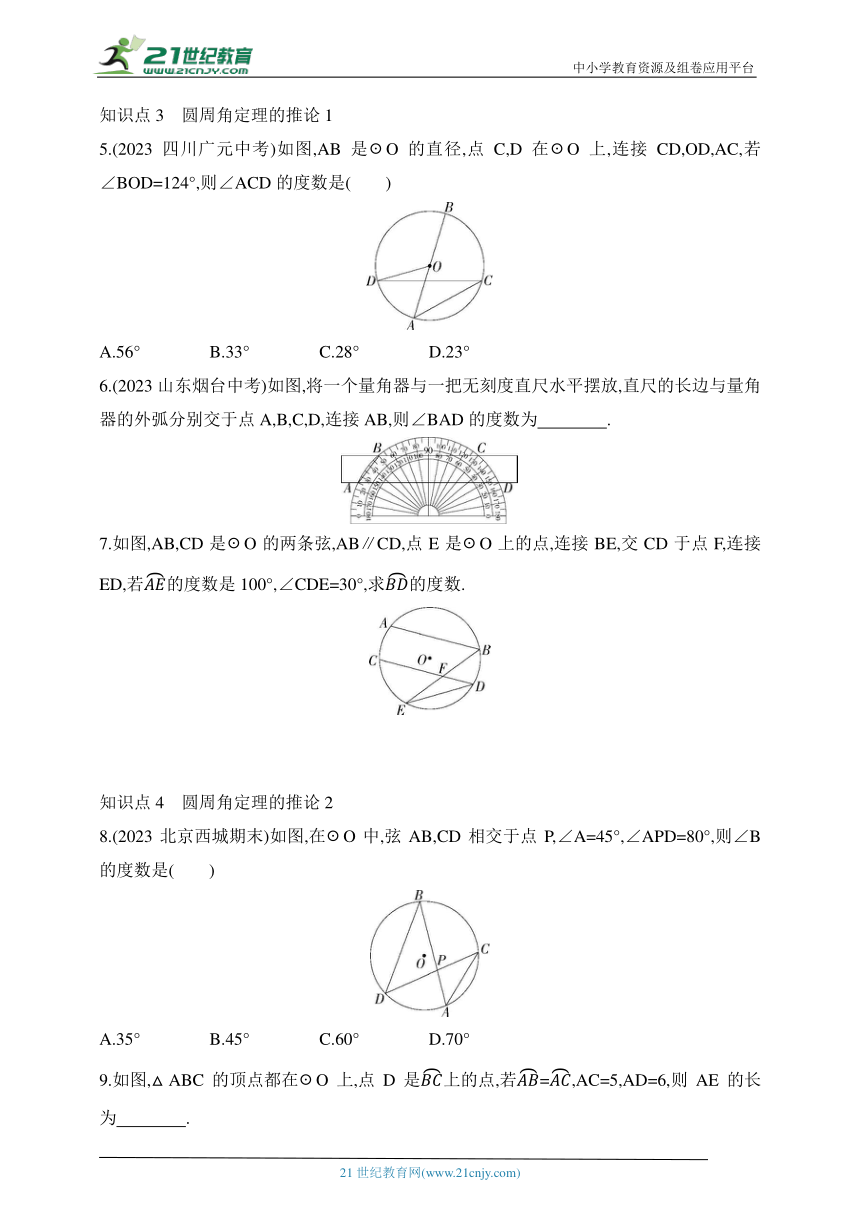
5.(2023四川广元中考)如图,AB是☉O的直径,点C,D在☉O上,连接CD,OD,AC,若∠BOD=124°,则∠ACD的度数是( )
A.56° B.33° C.28° D.23°
6.(2023山东烟台中考)如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接AB,则∠BAD的度数为 .
7.如图,AB,CD是☉O的两条弦,AB∥CD,点E是☉O上的点,连接BE,交CD于点F,连接ED,若的度数是100°,∠CDE=30°,求的度数.
知识点4 圆周角定理的推论2
8.(2023北京西城期末)如图,在☉O中,弦AB,CD相交于点P,∠A=45°,∠APD=80°,则∠B的度数是( )
A.35° B.45° C.60° D.70°
9.如图,△ABC的顶点都在☉O上,点D是上的点,若=,AC=5,AD=6,则AE的长为 .
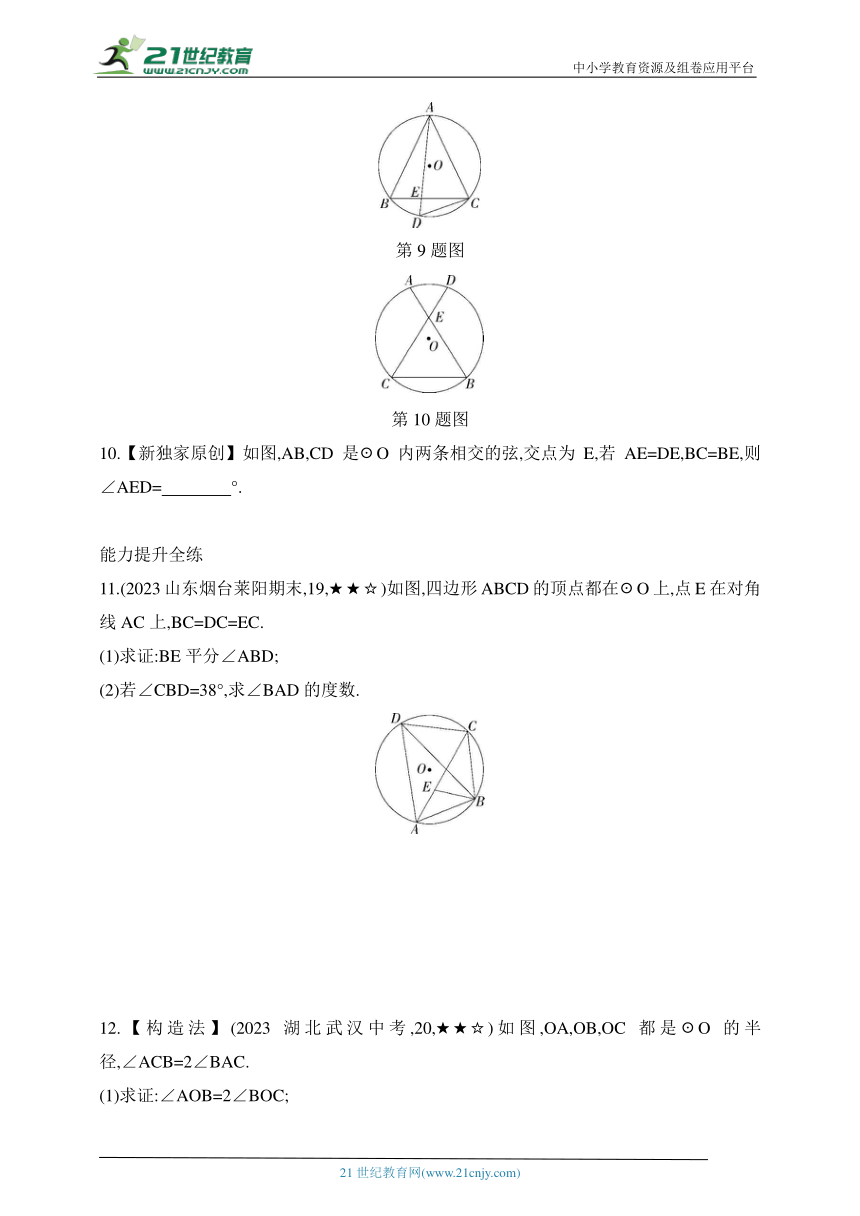
第9题图
第10题图
10.【新独家原创】如图,AB,CD是☉O内两条相交的弦,交点为E,若AE=DE,BC=BE,则∠AED= °.
能力提升全练
11.(2023山东烟台莱阳期末,19,★★☆)如图,四边形ABCD的顶点都在☉O上,点E在对角线AC上,BC=DC=EC.
(1)求证:BE平分∠ABD;
(2)若∠CBD=38°,求∠BAD的度数.
12.【构造法】(2023湖北武汉中考,20,★★☆)如图,OA,OB,OC都是☉O的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若AB=4,BC=,求☉O的半径.
素养探究全练
13.【抽象能力】【定弦对定角模型】(2023山东枣庄滕州模拟)船在航行过程中,船长常常通过测量角度来判断是否有触礁危险.如图,A,B两点表示两个灯塔,暗礁分布在经过A,B两点的一个圆形区域内,优弧ACB是有触礁危险的临界线,∠ACB是“危险角”.当船分别位于D,E,F,G四个位置时,船与两个灯塔的夹角小于“危险角”∠ACB的是( )
A.∠ADB B.∠AEB
C.∠AFB D.∠AGB
第五章 圆
4 圆周角和圆心角的关系
第1课时 圆周角定理及其推论1、2
答案全解全析
基础过关全练
1.A 选项A中的角顶点在圆上,且两边与圆相交,是圆周角,故选A.
2.D ∵∠AOB=2∠C,∠C=55°,∴∠AOB=110°,故选D.
3.B ∵∠AOB=80°,∴∠C=∠AOB=40°.
4.答案7
解析如图,作OD⊥BC于点D,连接OB,OC.
∵∠BAC=60°,∴∠BOC=2∠BAC=120°.
∵OD⊥BC,OB=OC,∴∠BOD=∠BOC=60°,BD=CD.
∴BD=BO·sin∠BOD=7×sin 60°=7×=.∴BC=2BD=7.
5.C ∵∠BOD=124°,∴的度数=124°.
∵AB是☉O的直径,∴的度数=180°-124°=56°.
∴∠ACD=×的度数=28°,故选C.
6.答案52.5°
解析由题图知的度数=155°-50°=105°.
∴∠BAD=×的度数=52.5°.
7.解析∵的度数是100°,∴∠B=50°.
∵AB∥CD,∴∠BFD=∠B=50°.
∵∠CDE=30°,∴∠E=∠BFD-∠CDE=20°.∴的度数=40°.
8.A ∵∠A=∠D=45°,∠APD=∠B+∠D,
∴∠B=∠APD-∠D=80°-45°=35°,故选A.
9.答案
解析∵=,∴∠ACB=∠B=∠D.
又∠DAC=∠CAE,∴△DAC∽△CAE.
∴=,即=.∴AE=.
10.答案60
解析如图,连接AC,BD.
在△AEC和△DEB中,
∴△AEC≌△DEB(ASA).
∴EC=EB.∵BC=BE,∴EC=BC=BE.∴△ECB为等边三角形.∴∠CEB=60°.
∴∠AED=∠CEB=60°.
能力提升全练
11.解析(1)证明:∵BC=DC,∴∠CBD=∠CDB.
∵∠CDB=∠BAC,∴∠CBD=∠BAC.
∵EC=BC,∴∠CEB=∠CBE.
∵∠CEB=∠BAC+∠ABE,∠CBE=∠CBD+∠DBE,
∴∠ABE=∠DBE,即BE平分∠ABD.
(2)∵∠CBD=38°,∠CBD=∠BAC,∠CBD=∠CAD,
∴∠BAD=∠BAC+∠CAD=2∠CBD=2×38°=76°.
12.解析(1)证明:由圆周角定理得,∠ACB=∠AOB,∠BAC=∠BOC.
∵∠ACB=2∠BAC,∴∠AOB=2∠BOC.
(2)如图,过点O作半径OD⊥AB于点E,连接BD,则∠DOB=∠AOB,AE=BE.
∵∠AOB=2∠BOC,
∴∠DOB=∠BOC.∴BD=BC.
∵AB=4,BC=,∴BE=2,DB=.在Rt△BDE中,∵∠DEB=90°,∴DE==1.
在Rt△BOE中,∵∠OEB=90°,∴OB2=OE2+BE2,即OB2=(OB-1)2+22,
∴OB=,即☉O的半径是.
素养探究全练
13.A ∵∠ACB=∠AEB,∠AEB>∠ADB,∴∠ACB>∠ADB,故选A.
经典模型 定弦对定角模型
在同圆或等圆中,同一条弦所对的劣弧(或优弧)上的圆周角都相等.反过来,若某线段所对同一侧的角都相等,则这些角的顶点都在同一圆上,据此常构造辅助圆解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
第五章 圆
4 圆周角和圆心角的关系
第1课时 圆周角定理及其推论1、2
基础过关全练
知识点1 圆周角
1.(2021河南开封期末)下列图形中的角是圆周角的是( )
A B C D
知识点2 圆周角定理
2.(2023河南中考)如图,点A,B,C在☉O上,若∠C=55°,则∠AOB的度数为( )
A.95° B.100° C.105° D.110°
3.(2022贵州铜仁中考)如图,OA,OB是☉O的两条半径,点C在☉O上,若∠AOB=80°,则∠C的度数为( )
A.30° B.40° C.50° D.60°
4.【构造法】(2023四川广安中考)如图,△ABC的三个顶点在☉O上,圆的半径为7,∠BAC=60°,则弦BC的长度为 .
知识点3 圆周角定理的推论1
5.(2023四川广元中考)如图,AB是☉O的直径,点C,D在☉O上,连接CD,OD,AC,若∠BOD=124°,则∠ACD的度数是( )
A.56° B.33° C.28° D.23°
6.(2023山东烟台中考)如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A,B,C,D,连接AB,则∠BAD的度数为 .
7.如图,AB,CD是☉O的两条弦,AB∥CD,点E是☉O上的点,连接BE,交CD于点F,连接ED,若的度数是100°,∠CDE=30°,求的度数.
知识点4 圆周角定理的推论2
8.(2023北京西城期末)如图,在☉O中,弦AB,CD相交于点P,∠A=45°,∠APD=80°,则∠B的度数是( )
A.35° B.45° C.60° D.70°
9.如图,△ABC的顶点都在☉O上,点D是上的点,若=,AC=5,AD=6,则AE的长为 .
第9题图
第10题图
10.【新独家原创】如图,AB,CD是☉O内两条相交的弦,交点为E,若AE=DE,BC=BE,则∠AED= °.
能力提升全练
11.(2023山东烟台莱阳期末,19,★★☆)如图,四边形ABCD的顶点都在☉O上,点E在对角线AC上,BC=DC=EC.
(1)求证:BE平分∠ABD;
(2)若∠CBD=38°,求∠BAD的度数.
12.【构造法】(2023湖北武汉中考,20,★★☆)如图,OA,OB,OC都是☉O的半径,∠ACB=2∠BAC.
(1)求证:∠AOB=2∠BOC;
(2)若AB=4,BC=,求☉O的半径.
素养探究全练
13.【抽象能力】【定弦对定角模型】(2023山东枣庄滕州模拟)船在航行过程中,船长常常通过测量角度来判断是否有触礁危险.如图,A,B两点表示两个灯塔,暗礁分布在经过A,B两点的一个圆形区域内,优弧ACB是有触礁危险的临界线,∠ACB是“危险角”.当船分别位于D,E,F,G四个位置时,船与两个灯塔的夹角小于“危险角”∠ACB的是( )
A.∠ADB B.∠AEB
C.∠AFB D.∠AGB
第五章 圆
4 圆周角和圆心角的关系
第1课时 圆周角定理及其推论1、2
答案全解全析
基础过关全练
1.A 选项A中的角顶点在圆上,且两边与圆相交,是圆周角,故选A.
2.D ∵∠AOB=2∠C,∠C=55°,∴∠AOB=110°,故选D.
3.B ∵∠AOB=80°,∴∠C=∠AOB=40°.
4.答案7
解析如图,作OD⊥BC于点D,连接OB,OC.
∵∠BAC=60°,∴∠BOC=2∠BAC=120°.
∵OD⊥BC,OB=OC,∴∠BOD=∠BOC=60°,BD=CD.
∴BD=BO·sin∠BOD=7×sin 60°=7×=.∴BC=2BD=7.
5.C ∵∠BOD=124°,∴的度数=124°.
∵AB是☉O的直径,∴的度数=180°-124°=56°.
∴∠ACD=×的度数=28°,故选C.
6.答案52.5°
解析由题图知的度数=155°-50°=105°.
∴∠BAD=×的度数=52.5°.
7.解析∵的度数是100°,∴∠B=50°.
∵AB∥CD,∴∠BFD=∠B=50°.
∵∠CDE=30°,∴∠E=∠BFD-∠CDE=20°.∴的度数=40°.
8.A ∵∠A=∠D=45°,∠APD=∠B+∠D,
∴∠B=∠APD-∠D=80°-45°=35°,故选A.
9.答案
解析∵=,∴∠ACB=∠B=∠D.
又∠DAC=∠CAE,∴△DAC∽△CAE.
∴=,即=.∴AE=.
10.答案60
解析如图,连接AC,BD.
在△AEC和△DEB中,
∴△AEC≌△DEB(ASA).
∴EC=EB.∵BC=BE,∴EC=BC=BE.∴△ECB为等边三角形.∴∠CEB=60°.
∴∠AED=∠CEB=60°.
能力提升全练
11.解析(1)证明:∵BC=DC,∴∠CBD=∠CDB.
∵∠CDB=∠BAC,∴∠CBD=∠BAC.
∵EC=BC,∴∠CEB=∠CBE.
∵∠CEB=∠BAC+∠ABE,∠CBE=∠CBD+∠DBE,
∴∠ABE=∠DBE,即BE平分∠ABD.
(2)∵∠CBD=38°,∠CBD=∠BAC,∠CBD=∠CAD,
∴∠BAD=∠BAC+∠CAD=2∠CBD=2×38°=76°.
12.解析(1)证明:由圆周角定理得,∠ACB=∠AOB,∠BAC=∠BOC.
∵∠ACB=2∠BAC,∴∠AOB=2∠BOC.
(2)如图,过点O作半径OD⊥AB于点E,连接BD,则∠DOB=∠AOB,AE=BE.
∵∠AOB=2∠BOC,
∴∠DOB=∠BOC.∴BD=BC.
∵AB=4,BC=,∴BE=2,DB=.在Rt△BDE中,∵∠DEB=90°,∴DE==1.
在Rt△BOE中,∵∠OEB=90°,∴OB2=OE2+BE2,即OB2=(OB-1)2+22,
∴OB=,即☉O的半径是.
素养探究全练
13.A ∵∠ACB=∠AEB,∠AEB>∠ADB,∴∠ACB>∠ADB,故选A.
经典模型 定弦对定角模型
在同圆或等圆中,同一条弦所对的劣弧(或优弧)上的圆周角都相等.反过来,若某线段所对同一侧的角都相等,则这些角的顶点都在同一圆上,据此常构造辅助圆解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
