5.5 确定圆的条件课时练(含解析)
文档属性
| 名称 | 5.5 确定圆的条件课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 544.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:31:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
圆
5 确定圆的条件
基础过关全练
知识点1 确定圆的条件
1.(2023河北石家庄四十四中期末)下列条件中,不能确定一个圆的是( )
A.圆心与半径 B.平面上的三个已知点
C.以已知线段为直径 D.三角形的三个顶点
2.平面直角坐标系内的三个点A(1,-3)、B(0,-3)、C(2,-3) 确定一个圆.(填“能”或“不能”)
3.【山东常考·网格背景题】(2023山东济南历下期末)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立平面直角坐标系.
(1)过A,B,C三点的圆的圆心M的坐标为 ;
(2)求过A,B,C三点的圆的面积(结果保留π).
4.将图中的轮子复原,已知弧上三点A,B,C,连接AB,AC.
(1)画出该轮子的圆心(不写作法,保留作图痕迹);
(2)若△ABC是等腰三角形,底边BC=16 cm,腰AB=10 cm,求该轮子的半径.
知识点2 三角形的外接圆与外心
5.若一个三角形的外心在其内部,则这个三角形一定是( )
A.任意三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
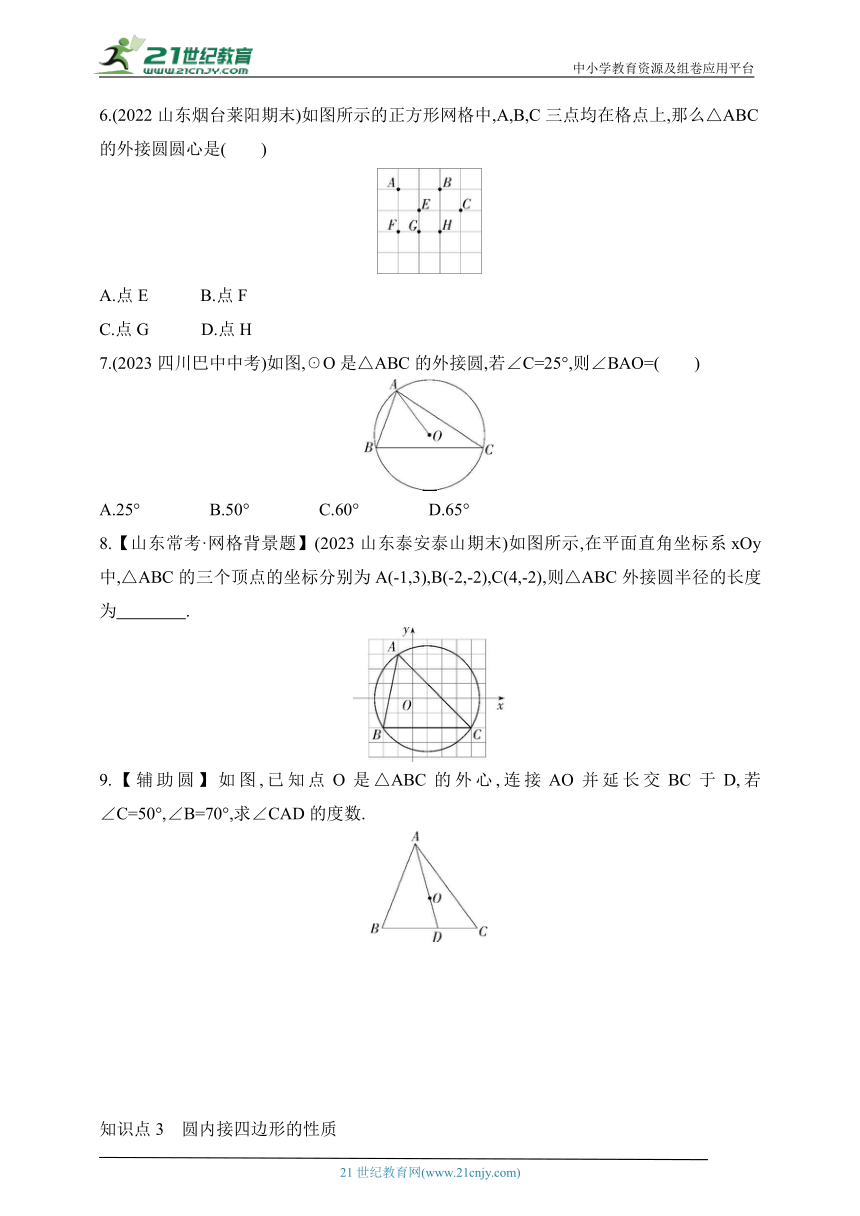
6.(2022山东烟台莱阳期末)如图所示的正方形网格中,A,B,C三点均在格点上,那么△ABC的外接圆圆心是( )
A.点E B.点F
C.点G D.点H
7.(2023四川巴中中考)如图,☉O是△ABC的外接圆,若∠C=25°,则∠BAO=( )
A.25° B.50° C.60° D.65°
8.【山东常考·网格背景题】(2023山东泰安泰山期末)如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(-1,3),B(-2,-2),C(4,-2),则△ABC外接圆半径的长度为 .
9.【辅助圆】如图,已知点O是△ABC的外心,连接AO并延长交BC于D,若∠C=50°,∠B=70°,求∠CAD的度数.
知识点3 圆内接四边形的性质
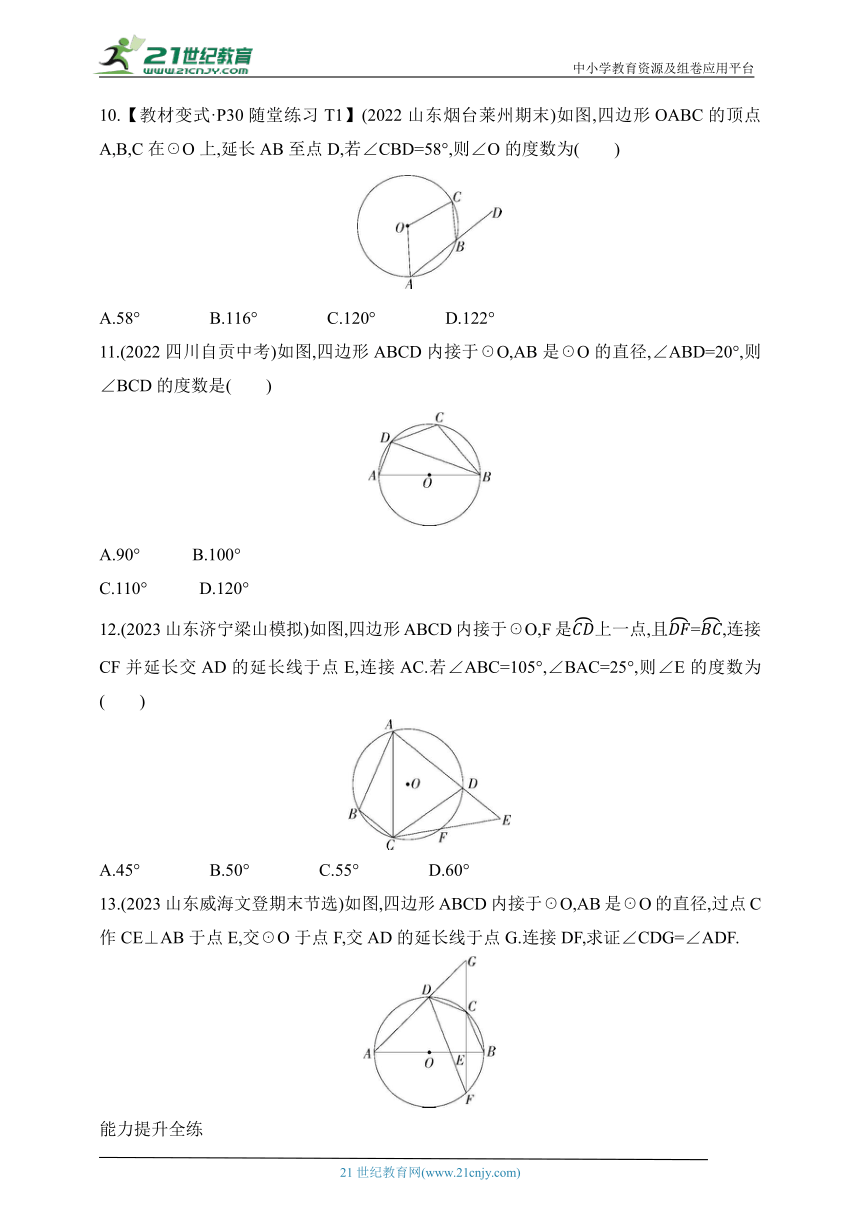
10.【教材变式·P30随堂练习T1】(2022山东烟台莱州期末)如图,四边形OABC的顶点A,B,C在☉O上,延长AB至点D,若∠CBD=58°,则∠O的度数为( )
A.58° B.116° C.120° D.122°
11.(2022四川自贡中考)如图,四边形ABCD内接于☉O,AB是☉O的直径,∠ABD=20°,则∠BCD的度数是( )
A.90° B.100°
C.110° D.120°
12.(2023山东济宁梁山模拟)如图,四边形ABCD内接于☉O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
13.(2023山东威海文登期末节选)如图,四边形ABCD内接于☉O,AB是☉O的直径,过点C作CE⊥AB于点E,交☉O于点F,交AD的延长线于点G.连接DF,求证∠CDG=∠ADF.
能力提升全练
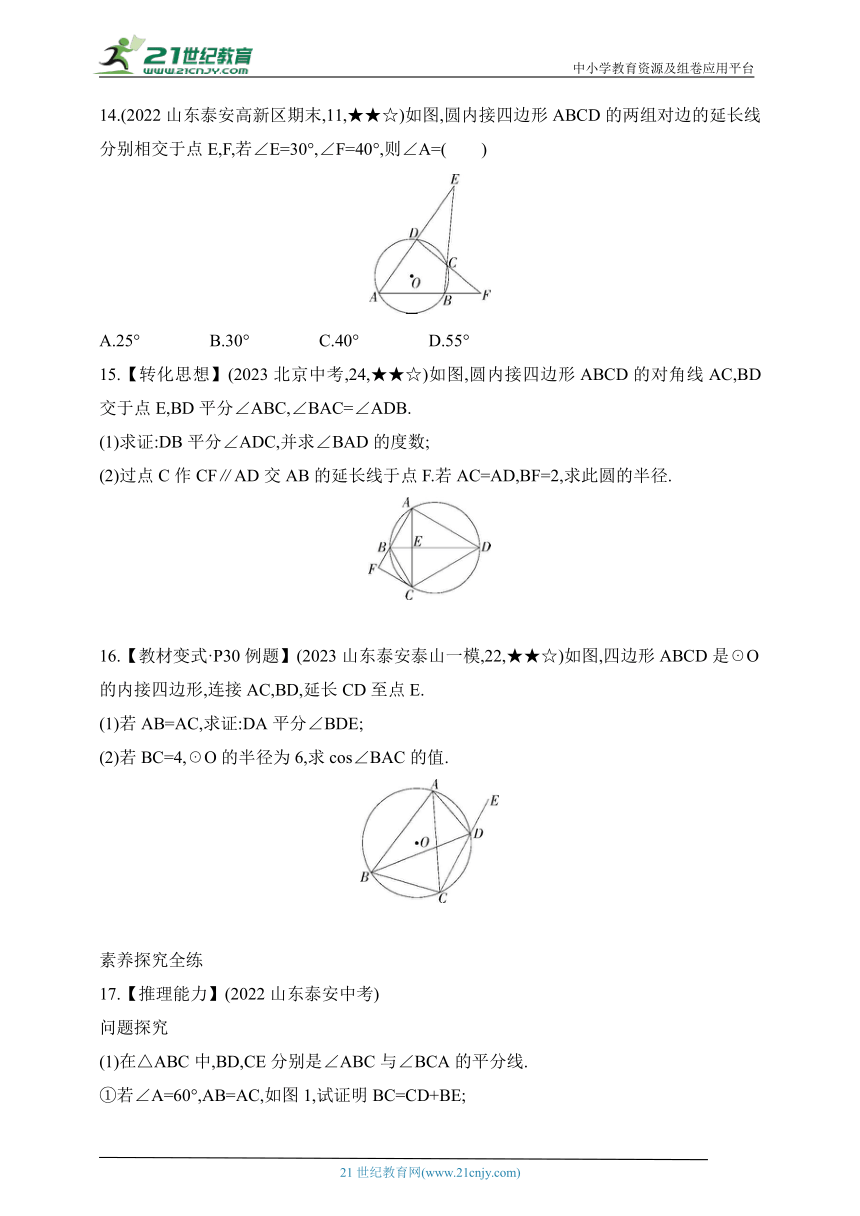
14.(2022山东泰安高新区期末,11,★★☆)如图,圆内接四边形ABCD的两组对边的延长线分别相交于点E,F,若∠E=30°,∠F=40°,则∠A=( )
A.25° B.30° C.40° D.55°
15.【转化思想】(2023北京中考,24,★★☆)如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证:DB平分∠ADC,并求∠BAD的度数;
(2)过点C作CF∥AD交AB的延长线于点F.若AC=AD,BF=2,求此圆的半径.
16.【教材变式·P30例题】(2023山东泰安泰山一模,22,★★☆)如图,四边形ABCD是☉O的内接四边形,连接AC,BD,延长CD至点E.
(1)若AB=AC,求证:DA平分∠BDE;
(2)若BC=4,☉O的半径为6,求cos∠BAC的值.
素养探究全练
17.【推理能力】(2022山东泰安中考)
问题探究
(1)在△ABC中,BD,CE分别是∠ABC与∠BCA的平分线.
①若∠A=60°,AB=AC,如图1,试证明BC=CD+BE;
②将①中的条件“AB=AC”去掉,其他条件不变,如图2,则①中的结论是否成立 并说明理由.
迁移运用
(2)若四边形ABCD是圆的内接四边形,且∠ACB=2∠ACD,∠CAD=2∠CAB,如图3,试探究线段AD,BC,AC之间的等量关系,并证明.
图1
图2
图3
答案全解全析
基础过关全练
1.B A项,已知圆心与半径能确定一个圆;B项,平面上的三个已知点可能在同一直线上,∴不一定能确定一个圆;C项,以已知线段为直径能确定一个圆;D项,已知三角形的三个顶点,能确定一个圆.故选B.
2.答案不能
解析点A(1,-3)、B(0,-3)、C(2,-3)在同一直线上,因此不能确定一个圆.
3.解析此题以带有网格的平面直角坐标系考查圆心的确定方法.
(1)如图所示,连接AB,BD,借助网格特点分别画出AB,BD的垂直平分线,两直线交于点M(1,-2),则点M就是过A,B,C三点的圆的圆心.故填(1,-2).
(2)如图,连接MB,由勾股定理得MB==,故过A,B,C三点的圆的面积为10π.
4.解析(1)如图所示,分别作弦AB和AC的垂直平分线,两直线交于点O,则点O即为所求作的圆心.
(2)如图,连接AO,OB,BC,BC交OA于D.
∵△ABC是等腰三角形,∴AB=AC,∴=,
∴AO⊥BC,∴BD=BC=8 cm.
∵AB=10 cm,∴AD==6 cm.
设该轮子的半径为R cm,
在Rt△BOD中,OB2=BD2+OD2,
即R2=82+(R-6)2,解得R=.
∴该轮子的半径为 cm.
5.C 锐角三角形的外心在其内部.
6.C 利用网格可以判断线段AB和线段BC的垂直平分线交于点G,则△ABC的外接圆圆心是点G,故选C.
7.D 连接OB(图略).
∵∠C=25°,∴∠AOB=2∠C=50°.∵OA=OB,∴∠BAO=∠ABO==65°.故选D.
8.答案
解析设△ABC的外心为点M.∵B(-2,-2),C(4,-2),∴点M必在直线x=1上.
如图,AC的垂直平分线过点(1,0),故M的坐标为(1,0).连接MB.由勾股定理得MB==.
∴△ABC的外接圆半径为.
方法解读 确定圆弧的圆心,只需在圆弧上找到三个点,确定这三个点所构成的三角形的外心即可.此外,由垂径定理的推论可知,圆弧上任意两条弦的垂直平分线的交点即为圆心.特别地,在网格中确定三角形的外接圆圆心,可借助网格特点,快速找到两边的垂直平分线的交点,即圆心.
9.解析如图,作△ABC的外接圆,延长AD交☉O于点E,连接BE,则∠ABE=90°.∵∠ABC=70°,
∴∠CBE=90°-∠ABC=20°.∴∠CAD=∠CBE=20°.
10.B 在优弧AC上任取一点E,连接AE,CE,如图,
∵四边形AECB内接于☉O,∴∠AEC=∠CBD=58°.
∴∠AOC=2∠AEC=2×58°=116°.故选B.
11.C ∵AB是☉O的直径,∴∠ADB=90°.∵∠ABD=20°,∴∠A=70°.∵四边形ABCD是☉O的内接四边形,∴∠A+∠BCD=180°.∴∠BCD=110°.故选C.
12.B ∵四边形ABCD内接于☉O,∠ABC=105°,
∴∠ADC=180°-∠ABC=180°-105°=75°.
∵=,∠BAC=25°,∴∠DCE=∠BAC=25°.
∴∠E=∠ADC-∠DCE=75°-25°=50°.故选B.
13.证明 ∵CE⊥AB,AB是☉O的直径,
∴=.∴∠ADF=∠ABC.
∵四边形ABCD内接于☉O,
∴∠CDG=∠ABC,∴∠CDG=∠ADF.
能力提升全练
14.D ∵四边形ABCD内接于☉O,∴∠ADC=∠FBC.
∵∠ADC=180°-∠A-∠F,∠FBC=∠A+∠E,
∴180°-∠A-∠F=∠A+∠E,
∴2∠A=180°-(∠F+∠E)=180°-(40°+30°)=110°,
∴∠A=55°.故选D.
15.解析(1)证明:∵∠BAC=∠ADB,∠BAC=∠CDB,
∴∠ADB=∠CDB.∴DB平分∠ADC.
∵BD平分∠ABC,∴∠ABD=∠CBD,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
即∠ABD+∠CBD+∠ADB+∠CDB=180°.
∴∠ABD+∠ADB=90°.∴∠BAD=90°.
(2)∵∠BAD=90°,∴BD是圆的直径.
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴=.∴AD=CD.
∵AC=AD,∴AC=AD=CD,
∴△ACD是等边三角形.∴∠ADC=60°.
∴∠BDC=∠ADC=30°.
∵CF∥AD,∴∠F+∠BAD=180°.∴∠F=90°.
∵四边形ABCD是圆内接四边形,
∴∠FBC=∠ADC=60°.∴∠BCF=30°.
∴BC=2BF=4.
∵∠BCD=90°,∠BDC=30°,∴BD=2BC=8.
∴此圆的半径是4.
16.解析(1)证明:∵四边形ABCD是☉O的内接四边形,∴∠ABC=∠ADE.
∵AB=AC,∴∠ABC=∠ACB.
∵∠ADB=∠ACB,∴∠ADB=∠ADE.
∴DA平分∠BDE.
(2)如图,连接CO并延长交☉O于点F,连接BF.
∵CF是☉O的直径,∴∠CBF=90°.
在Rt△BCF中,BC=4,CF=12,
∴BF===8.
∴cos∠BFC===.
∵∠BAC=∠BFC,∴cos∠BAC=cos∠BFC=.
∴cos∠BAC的值为.
素养探究全练
17.解析(1)①证明:∵∠A=60°,AB=AC,
∴△ABC是等边三角形,∴AB=AC=BC,
又∵BD,CE分别是∠ABC,∠BCA的平分线,
∴点D,E分别是AC,AB的中点,
∴BE=AB=BC,CD=AC=BC,
∴BC=CD+BE.
②结论成立.
理由:如图,设BD与CE交于点F,
∵BD,CE分别是∠ABC与∠BCA的平分线,
∴∠1=∠2,∠3=∠4,∵∠A=60°,
∴∠ABC+∠BCA=120°,
∴∠1+∠3=∠ABC+∠BCA=60°,
∴∠BFC=180°-(∠1+∠3)=120°,
∴∠5=∠6=60°,
在BC上截取BG=BE,连接FG,
则△BEF≌△BGF,∴∠7=∠6=60°,
∴∠8=∠BFC-∠7=60°,∴∠8=∠5,
∴△DFC≌△GFC,∴DC=GC,
∴BC=GC+BG=CD+BE.
(2)AC=AD+BC.
证明:∵四边形ABCD是圆的内接四边形,
∴∠DAB+∠BCD=180°.
∵∠DAC=2∠CAB,∠BCA=2∠ACD,
∴∠DAB+∠BCD=(∠DAC+∠CAB)+(∠BCA+∠ACD)=(2∠CAB+∠CAB)+(2∠ACD+∠ACD)=3∠CAB+3∠ACD=180°,
∴∠CAB+∠ACD=60°.
作点B关于AC的对称点E,
连接CE,EA,AE与CD交于点F,如图,
∴∠CAB=∠1,BC=CE,
∴∠1+∠ACD=60°,
∴∠AFC=120°,∴∠2=∠3=60°.
在AC上截取AG=AD,连接FG,
∵∠DAC=2∠CAB,∠CAB=∠1,∴∠DAC=2∠1,
∴∠1=∠DAF,∴△DAF≌△GAF,∴∠4=∠2=60°,
∴∠5=∠AFC-∠4=60°,∴∠3=∠5.
∵∠BCA=2∠ACD,∠BCA=∠ECA,
∴∠ECA=2∠ACD,∴∠ACD=∠6,
∴△CFG≌△CFE,
∴CG=CE,∴AC=AG+CG=AD+CE=AD+BC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
圆
5 确定圆的条件
基础过关全练
知识点1 确定圆的条件
1.(2023河北石家庄四十四中期末)下列条件中,不能确定一个圆的是( )
A.圆心与半径 B.平面上的三个已知点
C.以已知线段为直径 D.三角形的三个顶点
2.平面直角坐标系内的三个点A(1,-3)、B(0,-3)、C(2,-3) 确定一个圆.(填“能”或“不能”)
3.【山东常考·网格背景题】(2023山东济南历下期末)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立平面直角坐标系.
(1)过A,B,C三点的圆的圆心M的坐标为 ;
(2)求过A,B,C三点的圆的面积(结果保留π).
4.将图中的轮子复原,已知弧上三点A,B,C,连接AB,AC.
(1)画出该轮子的圆心(不写作法,保留作图痕迹);
(2)若△ABC是等腰三角形,底边BC=16 cm,腰AB=10 cm,求该轮子的半径.
知识点2 三角形的外接圆与外心
5.若一个三角形的外心在其内部,则这个三角形一定是( )
A.任意三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
6.(2022山东烟台莱阳期末)如图所示的正方形网格中,A,B,C三点均在格点上,那么△ABC的外接圆圆心是( )
A.点E B.点F
C.点G D.点H
7.(2023四川巴中中考)如图,☉O是△ABC的外接圆,若∠C=25°,则∠BAO=( )
A.25° B.50° C.60° D.65°
8.【山东常考·网格背景题】(2023山东泰安泰山期末)如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(-1,3),B(-2,-2),C(4,-2),则△ABC外接圆半径的长度为 .
9.【辅助圆】如图,已知点O是△ABC的外心,连接AO并延长交BC于D,若∠C=50°,∠B=70°,求∠CAD的度数.
知识点3 圆内接四边形的性质
10.【教材变式·P30随堂练习T1】(2022山东烟台莱州期末)如图,四边形OABC的顶点A,B,C在☉O上,延长AB至点D,若∠CBD=58°,则∠O的度数为( )
A.58° B.116° C.120° D.122°
11.(2022四川自贡中考)如图,四边形ABCD内接于☉O,AB是☉O的直径,∠ABD=20°,则∠BCD的度数是( )
A.90° B.100°
C.110° D.120°
12.(2023山东济宁梁山模拟)如图,四边形ABCD内接于☉O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
13.(2023山东威海文登期末节选)如图,四边形ABCD内接于☉O,AB是☉O的直径,过点C作CE⊥AB于点E,交☉O于点F,交AD的延长线于点G.连接DF,求证∠CDG=∠ADF.
能力提升全练
14.(2022山东泰安高新区期末,11,★★☆)如图,圆内接四边形ABCD的两组对边的延长线分别相交于点E,F,若∠E=30°,∠F=40°,则∠A=( )
A.25° B.30° C.40° D.55°
15.【转化思想】(2023北京中考,24,★★☆)如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证:DB平分∠ADC,并求∠BAD的度数;
(2)过点C作CF∥AD交AB的延长线于点F.若AC=AD,BF=2,求此圆的半径.
16.【教材变式·P30例题】(2023山东泰安泰山一模,22,★★☆)如图,四边形ABCD是☉O的内接四边形,连接AC,BD,延长CD至点E.
(1)若AB=AC,求证:DA平分∠BDE;
(2)若BC=4,☉O的半径为6,求cos∠BAC的值.
素养探究全练
17.【推理能力】(2022山东泰安中考)
问题探究
(1)在△ABC中,BD,CE分别是∠ABC与∠BCA的平分线.
①若∠A=60°,AB=AC,如图1,试证明BC=CD+BE;
②将①中的条件“AB=AC”去掉,其他条件不变,如图2,则①中的结论是否成立 并说明理由.
迁移运用
(2)若四边形ABCD是圆的内接四边形,且∠ACB=2∠ACD,∠CAD=2∠CAB,如图3,试探究线段AD,BC,AC之间的等量关系,并证明.
图1
图2
图3
答案全解全析
基础过关全练
1.B A项,已知圆心与半径能确定一个圆;B项,平面上的三个已知点可能在同一直线上,∴不一定能确定一个圆;C项,以已知线段为直径能确定一个圆;D项,已知三角形的三个顶点,能确定一个圆.故选B.
2.答案不能
解析点A(1,-3)、B(0,-3)、C(2,-3)在同一直线上,因此不能确定一个圆.
3.解析此题以带有网格的平面直角坐标系考查圆心的确定方法.
(1)如图所示,连接AB,BD,借助网格特点分别画出AB,BD的垂直平分线,两直线交于点M(1,-2),则点M就是过A,B,C三点的圆的圆心.故填(1,-2).
(2)如图,连接MB,由勾股定理得MB==,故过A,B,C三点的圆的面积为10π.
4.解析(1)如图所示,分别作弦AB和AC的垂直平分线,两直线交于点O,则点O即为所求作的圆心.
(2)如图,连接AO,OB,BC,BC交OA于D.
∵△ABC是等腰三角形,∴AB=AC,∴=,
∴AO⊥BC,∴BD=BC=8 cm.
∵AB=10 cm,∴AD==6 cm.
设该轮子的半径为R cm,
在Rt△BOD中,OB2=BD2+OD2,
即R2=82+(R-6)2,解得R=.
∴该轮子的半径为 cm.
5.C 锐角三角形的外心在其内部.
6.C 利用网格可以判断线段AB和线段BC的垂直平分线交于点G,则△ABC的外接圆圆心是点G,故选C.
7.D 连接OB(图略).
∵∠C=25°,∴∠AOB=2∠C=50°.∵OA=OB,∴∠BAO=∠ABO==65°.故选D.
8.答案
解析设△ABC的外心为点M.∵B(-2,-2),C(4,-2),∴点M必在直线x=1上.
如图,AC的垂直平分线过点(1,0),故M的坐标为(1,0).连接MB.由勾股定理得MB==.
∴△ABC的外接圆半径为.
方法解读 确定圆弧的圆心,只需在圆弧上找到三个点,确定这三个点所构成的三角形的外心即可.此外,由垂径定理的推论可知,圆弧上任意两条弦的垂直平分线的交点即为圆心.特别地,在网格中确定三角形的外接圆圆心,可借助网格特点,快速找到两边的垂直平分线的交点,即圆心.
9.解析如图,作△ABC的外接圆,延长AD交☉O于点E,连接BE,则∠ABE=90°.∵∠ABC=70°,
∴∠CBE=90°-∠ABC=20°.∴∠CAD=∠CBE=20°.
10.B 在优弧AC上任取一点E,连接AE,CE,如图,
∵四边形AECB内接于☉O,∴∠AEC=∠CBD=58°.
∴∠AOC=2∠AEC=2×58°=116°.故选B.
11.C ∵AB是☉O的直径,∴∠ADB=90°.∵∠ABD=20°,∴∠A=70°.∵四边形ABCD是☉O的内接四边形,∴∠A+∠BCD=180°.∴∠BCD=110°.故选C.
12.B ∵四边形ABCD内接于☉O,∠ABC=105°,
∴∠ADC=180°-∠ABC=180°-105°=75°.
∵=,∠BAC=25°,∴∠DCE=∠BAC=25°.
∴∠E=∠ADC-∠DCE=75°-25°=50°.故选B.
13.证明 ∵CE⊥AB,AB是☉O的直径,
∴=.∴∠ADF=∠ABC.
∵四边形ABCD内接于☉O,
∴∠CDG=∠ABC,∴∠CDG=∠ADF.
能力提升全练
14.D ∵四边形ABCD内接于☉O,∴∠ADC=∠FBC.
∵∠ADC=180°-∠A-∠F,∠FBC=∠A+∠E,
∴180°-∠A-∠F=∠A+∠E,
∴2∠A=180°-(∠F+∠E)=180°-(40°+30°)=110°,
∴∠A=55°.故选D.
15.解析(1)证明:∵∠BAC=∠ADB,∠BAC=∠CDB,
∴∠ADB=∠CDB.∴DB平分∠ADC.
∵BD平分∠ABC,∴∠ABD=∠CBD,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
即∠ABD+∠CBD+∠ADB+∠CDB=180°.
∴∠ABD+∠ADB=90°.∴∠BAD=90°.
(2)∵∠BAD=90°,∴BD是圆的直径.
∵BD平分∠ABC,∴∠ABD=∠CBD,
∴=.∴AD=CD.
∵AC=AD,∴AC=AD=CD,
∴△ACD是等边三角形.∴∠ADC=60°.
∴∠BDC=∠ADC=30°.
∵CF∥AD,∴∠F+∠BAD=180°.∴∠F=90°.
∵四边形ABCD是圆内接四边形,
∴∠FBC=∠ADC=60°.∴∠BCF=30°.
∴BC=2BF=4.
∵∠BCD=90°,∠BDC=30°,∴BD=2BC=8.
∴此圆的半径是4.
16.解析(1)证明:∵四边形ABCD是☉O的内接四边形,∴∠ABC=∠ADE.
∵AB=AC,∴∠ABC=∠ACB.
∵∠ADB=∠ACB,∴∠ADB=∠ADE.
∴DA平分∠BDE.
(2)如图,连接CO并延长交☉O于点F,连接BF.
∵CF是☉O的直径,∴∠CBF=90°.
在Rt△BCF中,BC=4,CF=12,
∴BF===8.
∴cos∠BFC===.
∵∠BAC=∠BFC,∴cos∠BAC=cos∠BFC=.
∴cos∠BAC的值为.
素养探究全练
17.解析(1)①证明:∵∠A=60°,AB=AC,
∴△ABC是等边三角形,∴AB=AC=BC,
又∵BD,CE分别是∠ABC,∠BCA的平分线,
∴点D,E分别是AC,AB的中点,
∴BE=AB=BC,CD=AC=BC,
∴BC=CD+BE.
②结论成立.
理由:如图,设BD与CE交于点F,
∵BD,CE分别是∠ABC与∠BCA的平分线,
∴∠1=∠2,∠3=∠4,∵∠A=60°,
∴∠ABC+∠BCA=120°,
∴∠1+∠3=∠ABC+∠BCA=60°,
∴∠BFC=180°-(∠1+∠3)=120°,
∴∠5=∠6=60°,
在BC上截取BG=BE,连接FG,
则△BEF≌△BGF,∴∠7=∠6=60°,
∴∠8=∠BFC-∠7=60°,∴∠8=∠5,
∴△DFC≌△GFC,∴DC=GC,
∴BC=GC+BG=CD+BE.
(2)AC=AD+BC.
证明:∵四边形ABCD是圆的内接四边形,
∴∠DAB+∠BCD=180°.
∵∠DAC=2∠CAB,∠BCA=2∠ACD,
∴∠DAB+∠BCD=(∠DAC+∠CAB)+(∠BCA+∠ACD)=(2∠CAB+∠CAB)+(2∠ACD+∠ACD)=3∠CAB+3∠ACD=180°,
∴∠CAB+∠ACD=60°.
作点B关于AC的对称点E,
连接CE,EA,AE与CD交于点F,如图,
∴∠CAB=∠1,BC=CE,
∴∠1+∠ACD=60°,
∴∠AFC=120°,∴∠2=∠3=60°.
在AC上截取AG=AD,连接FG,
∵∠DAC=2∠CAB,∠CAB=∠1,∴∠DAC=2∠1,
∴∠1=∠DAF,∴△DAF≌△GAF,∴∠4=∠2=60°,
∴∠5=∠AFC-∠4=60°,∴∠3=∠5.
∵∠BCA=2∠ACD,∠BCA=∠ECA,
∴∠ECA=2∠ACD,∴∠ACD=∠6,
∴△CFG≌△CFE,
∴CG=CE,∴AC=AG+CG=AD+CE=AD+BC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
