5.7 切线长定理课时练(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
圆
*7 切线长定理
基础过关全练
知识点 切线长及切线长定理
1.(2023湖南怀化三模)如图,AB,AC,BD是☉O的切线,切点分别是P,C,D.若AB=10,AC=6,则BD的长是(M9205008)( )
A.3 B.4 C.5 D.6
2.【构造法】(2022湖北恩施州中考)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,☉O为Rt△ABC的内切圆,则图中阴影部分的面积为 (结果保留π).(M9205008)
第2题图
第3题图
3.如图,PA、PB是☉O的切线,A、B为切点,点C、D在☉O上.若∠P=102°,则∠A+∠C= °.
4.【一题多变·已知切线长求三角形周长】(2022山东烟台芝罘期末)如图,PA,PB切☉O于点A,B,PA=10,CD切☉O于点E,交PA,PB于C,D两点,则△PCD的周长是 .(M9205008)
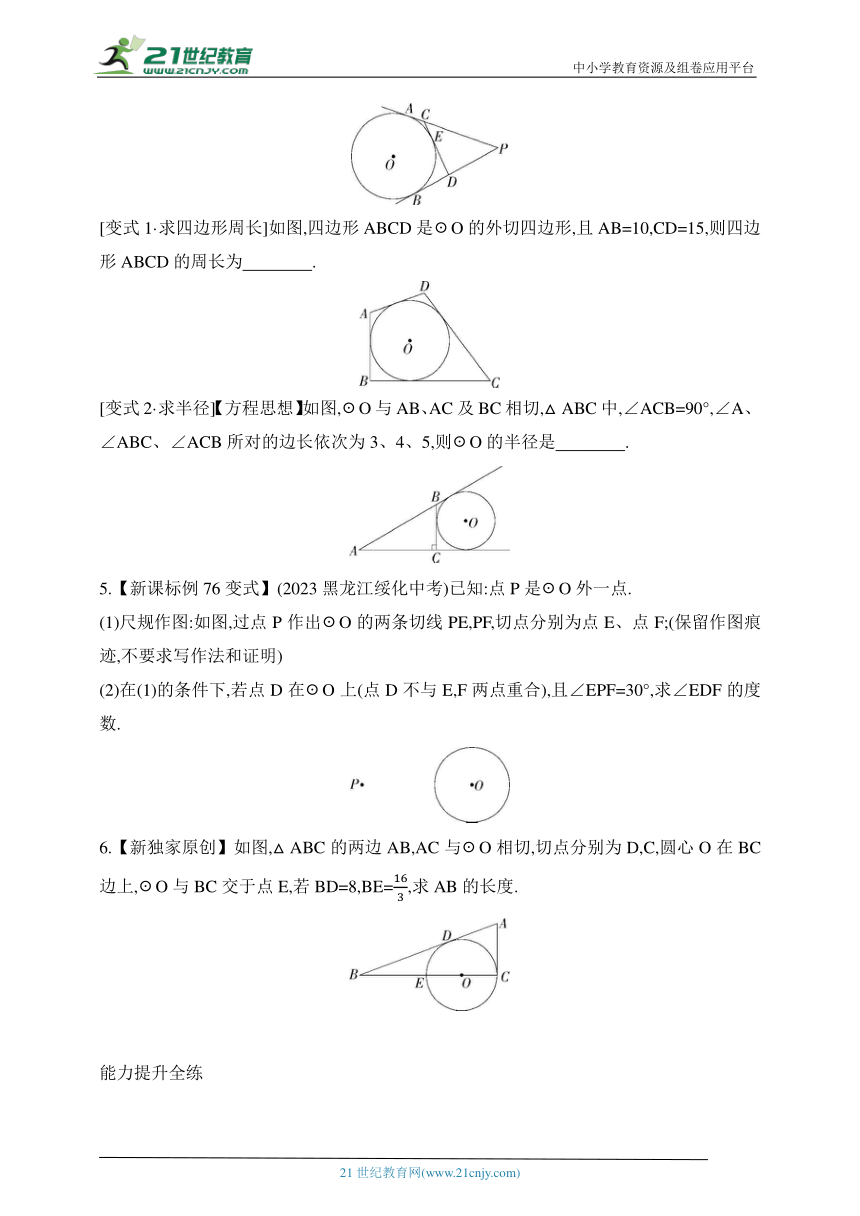
[变式1·求四边形周长]如图,四边形ABCD是☉O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 .
[变式2·求半径]【方程思想】如图,☉O与AB、AC及BC相切,△ABC中,∠ACB=90°,∠A、∠ABC、∠ACB所对的边长依次为3、4、5,则☉O的半径是 .
5.【新课标例76变式】(2023黑龙江绥化中考)已知:点P是☉O外一点.
(1)尺规作图:如图,过点P作出☉O的两条切线PE,PF,切点分别为点E、点F;(保留作图痕迹,不要求写作法和证明)
(2)在(1)的条件下,若点D在☉O上(点D不与E,F两点重合),且∠EPF=30°,求∠EDF的度数.
6.【新独家原创】如图,△ABC的两边AB,AC与☉O相切,切点分别为D,C,圆心O在BC边上,☉O与BC交于点E,若BD=8,BE=,求AB的长度.
能力提升全练
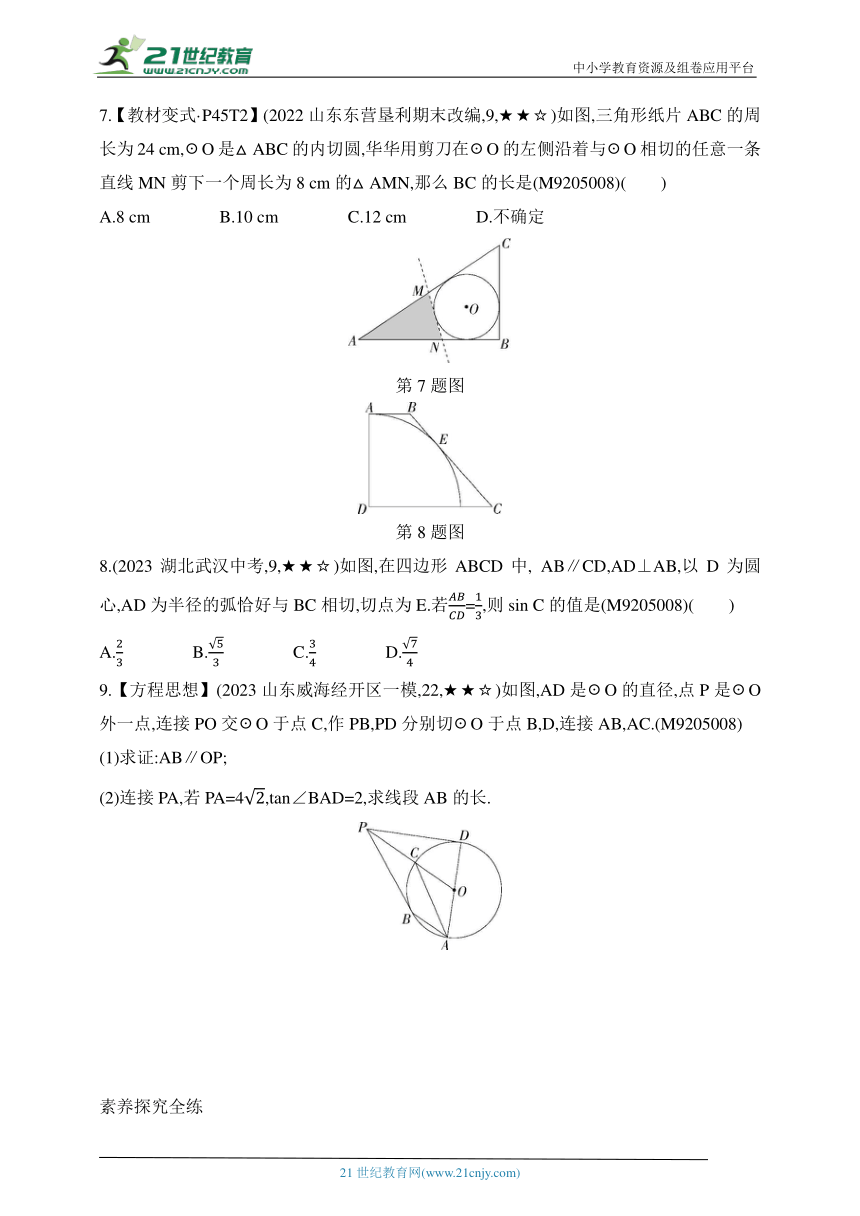
7.【教材变式·P45T2】(2022山东东营垦利期末改编,9,★★☆)如图,三角形纸片ABC的周长为24 cm,☉O是△ABC的内切圆,华华用剪刀在☉O的左侧沿着与☉O相切的任意一条直线MN剪下一个周长为8 cm的△AMN,那么BC的长是(M9205008)( )
A.8 cm B.10 cm C.12 cm D.不确定
第7题图
第8题图
8.(2023湖北武汉中考,9,★★☆)如图,在四边形ABCD中, AB∥CD,AD⊥AB,以D为圆心,AD为半径的弧恰好与BC相切,切点为E.若=,则sin C的值是(M9205008)( )
A. B. C. D.
9.【方程思想】(2023山东威海经开区一模,22,★★☆)如图,AD是☉O的直径,点P是☉O外一点,连接PO交☉O于点C,作PB,PD分别切☉O于点B,D,连接AB,AC.(M9205008)
(1)求证:AB∥OP;
(2)连接PA,若PA=4,tan∠BAD=2,求线段AB的长.
素养探究全练
10.【抽象能力】(2021四川泸州中考改编)如图,☉O的直径AB=8,AM,BN是☉O的两条切线,DE与☉O相切于点E,并与AM,BN分别相交于D,C两点,BD,OC相交于点F,若CD=10,求BF的长.(M9205008)
答案全解全析
基础过关全练
1.B ∵AC,AP为☉O的切线,∴AC=AP=6.
∵BP,BD为☉O的切线,∴BP=BD.
∴BD=PB=AB-AP=10-6=4.故选B.
2.答案5-π
解析作OD⊥AC于点D,作OE⊥CB于点E,作OF⊥AB于点F,如图.
∵AC=4,BC=3,∠C=90°,
∴AB===5.
∵☉O为Rt△ABC的内切圆,
∴AD=AF,CD=CE,BE=BF.
易得四边形ODCE是正方形,OD=1.
∴图中阴影部分的面积为-1×1-π×12×=5-π.
方法解读 若直角三角形的两条直角边长分别为a,b,斜边长为c,则此直角三角形内切圆的半径r=(a+b-c).
3.答案219
解析连接AB(图略).∵PA、PB是☉O的切线,∴PA=PB,
∵∠P=102°,∴∠PAB=∠PBA=×(180°-∠P)=39°,
∵∠DAB+∠C=180°,∴∠PAD+∠C=∠PAB+∠DAB+∠C=39°+180°=219°.
4.答案20
解析∵PA,PB切☉O于点A,B,CD切☉O于点E,∴PA=PB=10,CA=CE,DE=DB.
∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+AC+DB+PD=PA+PB=10+10=20.
方法解读 利用切线长定理可进行等线段长的转化,往往把三角形的周长转化为两线段长的和,在具体解决问题时,要注意整体思想的运用.
[变式1]答案50
解析如图,设四边形ABCD的各边与☉O相切于点E,F,G,H,
则AE=AH,BE=BF,CF=CG,DH=DG,∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50.
[变式2]答案2
解析如图,设☉O分别与AB、AC及BC相切于点F、D、E,连接OD、OE.
由题意知AF=AD,BE=BF,CE=CD,OD⊥AD,OE⊥BC,∵∠ACB=90°,
∴四边形ODCE是正方形.设OD=r,则CD=CE=r,
∵BC=3,∴BE=BF=3-r.∵AB=5,AC=4,∴AF=AB+BF=5+3-r,AD=AC+CD=4+r.∴5+3-r=4+r,解得r=2.∴☉O的半径是2.
5.解析(1)如图,直线PE,PF为所求作的切线.
(2)连接OE、OF,如图.
∵PE,PF为☉O的两条切线,
∴OE⊥PE,OF⊥PF.∴∠OEP=∠OFP=90°.
∴∠EOF=180°-∠EPF=180°-30°=150°.
当点D在优弧EF上时,∠EDF=∠EOF=75°.
当点D'在劣弧EF上时,∠ED'F=180°-∠EOF=180°-75°=105°.
综上所述,∠EDF的度数为75°或105°.
6.解析如图,连接OD,设☉O的半径为r,AC的长为x.
∵AB,AC是☉O的切线,
∴∠ODB=90°,∠ACB=90°,AC=AD=x.
在Rt△ODB中,BD2+OD2=OB2,即82+r2=,
解得r=.∴BC=EC+BE=×2+=12.
∵tan B==,∴=,解得x=5,即AC=5.
∴AB=AD+DB=5+8=13.
能力提升全练
7.A 如图,设D,H,E,G分别是直线AB,MN,AC,BC与☉O的切点.
∵☉O是△ABC的内切圆,
∴BD=BG,CE=CG,MH=ME,NH=ND.
∴△AMN的周长=AM+MN+AN=AM+MH+NH+AN=AM+ME+ND+AN=AE+AD,
△ABC的周长=AD+AE+BD+CE+BC=AD+AE+BG+CG+BC=AD+AE+2BC.
∴2BC=△ABC的周长-△AMN的周长=24-8=16(cm).∴BC=8 cm.故选A.
8.B 如图,连接DB,DE,设AB=m.
∵=,∴CD=3AB=3m.
∵AD是☉D的半径,AD⊥AB,∴AB是☉D的切线.
∵☉D与BC相切于点E,
∴BC⊥DE,EB=AB=m,∠CBD=∠ABD.
∵AB∥CD,∴∠ABD=∠CDB.∴∠CBD=∠CDB.
∴CB=CD=3m.∴CE=CB-EB=3m-m=2m.
∵∠CED=90°,
∴DE===m.
∴sin C===,故选B.
9.解析(1)证明:如图,连接OB.
∵PB,PD分别切☉O于点B,D,
∴PB=PD.∵OB=OD,OP=OP,
∴△OBP≌△ODP.∴∠BOP=∠DOP=∠BOD.
∵∠BAD=∠BOD,∴∠BAD=∠DOP.
∴AB∥OP.
(2)如图,连接BD.
∵∠BAD=∠DOP,∴tan∠BAD=tan∠DOP=2.
在Rt△DOP中,tan∠DOP==2,∴DP=2OD.
∵AD=2OD,∴DP=AD.
∵PD与☉O相切于点D,∴∠ADP=90°.
∴∠DPA=∠DAP=45°.
∵PA=4,∴AD=AP·sin∠DPA=4.
∵AD是☉O的直径,∴∠ABD=90°.
∴tan∠BAD==2,∴BD=2AB.
∵AB2+BD2=AD2,∴AB2+4AB2=16.
∴AB= 或AB=- (舍去).
∴线段AB的长为 .
素养探究全练
10.解析如图,过点D作DG⊥BC于点G,延长CO,交DA的延长线于点H.
∵AM,BN是☉O的两条切线,DE与☉O相切于点E,
∴AD=DE,BC=CE,∠DAB=∠ABC=90°.
∵DG⊥BC,∴四边形ABGD为矩形.
∴AD=BG,AB=DG=8.
在Rt△DGC中,CD=10,
∴GC===6.
∵CD=DE+CE=AD+BC=10,
∴AD+BG+GC=10,∴AD=BG=2,∴BC=CG+BG=8.
∵∠DAB+∠ABC=180°,∴AD∥BC.
∴∠AHO=∠BCO,∠HAO=∠CBO.
∵OA=OB,∴△HAO≌△CBO.∴AH=BC=8.
∵AD=2,∴DH=AH+AD=10.
在Rt△ABD中,AD=2,AB=8,
∴BD===2,
∵AD∥BC,∴△DHF∽△BCF.∴=,
即=,解得BF=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
圆
*7 切线长定理
基础过关全练
知识点 切线长及切线长定理
1.(2023湖南怀化三模)如图,AB,AC,BD是☉O的切线,切点分别是P,C,D.若AB=10,AC=6,则BD的长是(M9205008)( )
A.3 B.4 C.5 D.6
2.【构造法】(2022湖北恩施州中考)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,☉O为Rt△ABC的内切圆,则图中阴影部分的面积为 (结果保留π).(M9205008)
第2题图
第3题图
3.如图,PA、PB是☉O的切线,A、B为切点,点C、D在☉O上.若∠P=102°,则∠A+∠C= °.
4.【一题多变·已知切线长求三角形周长】(2022山东烟台芝罘期末)如图,PA,PB切☉O于点A,B,PA=10,CD切☉O于点E,交PA,PB于C,D两点,则△PCD的周长是 .(M9205008)
[变式1·求四边形周长]如图,四边形ABCD是☉O的外切四边形,且AB=10,CD=15,则四边形ABCD的周长为 .
[变式2·求半径]【方程思想】如图,☉O与AB、AC及BC相切,△ABC中,∠ACB=90°,∠A、∠ABC、∠ACB所对的边长依次为3、4、5,则☉O的半径是 .
5.【新课标例76变式】(2023黑龙江绥化中考)已知:点P是☉O外一点.
(1)尺规作图:如图,过点P作出☉O的两条切线PE,PF,切点分别为点E、点F;(保留作图痕迹,不要求写作法和证明)
(2)在(1)的条件下,若点D在☉O上(点D不与E,F两点重合),且∠EPF=30°,求∠EDF的度数.
6.【新独家原创】如图,△ABC的两边AB,AC与☉O相切,切点分别为D,C,圆心O在BC边上,☉O与BC交于点E,若BD=8,BE=,求AB的长度.
能力提升全练
7.【教材变式·P45T2】(2022山东东营垦利期末改编,9,★★☆)如图,三角形纸片ABC的周长为24 cm,☉O是△ABC的内切圆,华华用剪刀在☉O的左侧沿着与☉O相切的任意一条直线MN剪下一个周长为8 cm的△AMN,那么BC的长是(M9205008)( )
A.8 cm B.10 cm C.12 cm D.不确定
第7题图
第8题图
8.(2023湖北武汉中考,9,★★☆)如图,在四边形ABCD中, AB∥CD,AD⊥AB,以D为圆心,AD为半径的弧恰好与BC相切,切点为E.若=,则sin C的值是(M9205008)( )
A. B. C. D.
9.【方程思想】(2023山东威海经开区一模,22,★★☆)如图,AD是☉O的直径,点P是☉O外一点,连接PO交☉O于点C,作PB,PD分别切☉O于点B,D,连接AB,AC.(M9205008)
(1)求证:AB∥OP;
(2)连接PA,若PA=4,tan∠BAD=2,求线段AB的长.
素养探究全练
10.【抽象能力】(2021四川泸州中考改编)如图,☉O的直径AB=8,AM,BN是☉O的两条切线,DE与☉O相切于点E,并与AM,BN分别相交于D,C两点,BD,OC相交于点F,若CD=10,求BF的长.(M9205008)
答案全解全析
基础过关全练
1.B ∵AC,AP为☉O的切线,∴AC=AP=6.
∵BP,BD为☉O的切线,∴BP=BD.
∴BD=PB=AB-AP=10-6=4.故选B.
2.答案5-π
解析作OD⊥AC于点D,作OE⊥CB于点E,作OF⊥AB于点F,如图.
∵AC=4,BC=3,∠C=90°,
∴AB===5.
∵☉O为Rt△ABC的内切圆,
∴AD=AF,CD=CE,BE=BF.
易得四边形ODCE是正方形,OD=1.
∴图中阴影部分的面积为-1×1-π×12×=5-π.
方法解读 若直角三角形的两条直角边长分别为a,b,斜边长为c,则此直角三角形内切圆的半径r=(a+b-c).
3.答案219
解析连接AB(图略).∵PA、PB是☉O的切线,∴PA=PB,
∵∠P=102°,∴∠PAB=∠PBA=×(180°-∠P)=39°,
∵∠DAB+∠C=180°,∴∠PAD+∠C=∠PAB+∠DAB+∠C=39°+180°=219°.
4.答案20
解析∵PA,PB切☉O于点A,B,CD切☉O于点E,∴PA=PB=10,CA=CE,DE=DB.
∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+AC+DB+PD=PA+PB=10+10=20.
方法解读 利用切线长定理可进行等线段长的转化,往往把三角形的周长转化为两线段长的和,在具体解决问题时,要注意整体思想的运用.
[变式1]答案50
解析如图,设四边形ABCD的各边与☉O相切于点E,F,G,H,
则AE=AH,BE=BF,CF=CG,DH=DG,∴AD+BC=AB+CD=25,
∴四边形ABCD的周长=AD+BC+AB+CD=25+25=50.
[变式2]答案2
解析如图,设☉O分别与AB、AC及BC相切于点F、D、E,连接OD、OE.
由题意知AF=AD,BE=BF,CE=CD,OD⊥AD,OE⊥BC,∵∠ACB=90°,
∴四边形ODCE是正方形.设OD=r,则CD=CE=r,
∵BC=3,∴BE=BF=3-r.∵AB=5,AC=4,∴AF=AB+BF=5+3-r,AD=AC+CD=4+r.∴5+3-r=4+r,解得r=2.∴☉O的半径是2.
5.解析(1)如图,直线PE,PF为所求作的切线.
(2)连接OE、OF,如图.
∵PE,PF为☉O的两条切线,
∴OE⊥PE,OF⊥PF.∴∠OEP=∠OFP=90°.
∴∠EOF=180°-∠EPF=180°-30°=150°.
当点D在优弧EF上时,∠EDF=∠EOF=75°.
当点D'在劣弧EF上时,∠ED'F=180°-∠EOF=180°-75°=105°.
综上所述,∠EDF的度数为75°或105°.
6.解析如图,连接OD,设☉O的半径为r,AC的长为x.
∵AB,AC是☉O的切线,
∴∠ODB=90°,∠ACB=90°,AC=AD=x.
在Rt△ODB中,BD2+OD2=OB2,即82+r2=,
解得r=.∴BC=EC+BE=×2+=12.
∵tan B==,∴=,解得x=5,即AC=5.
∴AB=AD+DB=5+8=13.
能力提升全练
7.A 如图,设D,H,E,G分别是直线AB,MN,AC,BC与☉O的切点.
∵☉O是△ABC的内切圆,
∴BD=BG,CE=CG,MH=ME,NH=ND.
∴△AMN的周长=AM+MN+AN=AM+MH+NH+AN=AM+ME+ND+AN=AE+AD,
△ABC的周长=AD+AE+BD+CE+BC=AD+AE+BG+CG+BC=AD+AE+2BC.
∴2BC=△ABC的周长-△AMN的周长=24-8=16(cm).∴BC=8 cm.故选A.
8.B 如图,连接DB,DE,设AB=m.
∵=,∴CD=3AB=3m.
∵AD是☉D的半径,AD⊥AB,∴AB是☉D的切线.
∵☉D与BC相切于点E,
∴BC⊥DE,EB=AB=m,∠CBD=∠ABD.
∵AB∥CD,∴∠ABD=∠CDB.∴∠CBD=∠CDB.
∴CB=CD=3m.∴CE=CB-EB=3m-m=2m.
∵∠CED=90°,
∴DE===m.
∴sin C===,故选B.
9.解析(1)证明:如图,连接OB.
∵PB,PD分别切☉O于点B,D,
∴PB=PD.∵OB=OD,OP=OP,
∴△OBP≌△ODP.∴∠BOP=∠DOP=∠BOD.
∵∠BAD=∠BOD,∴∠BAD=∠DOP.
∴AB∥OP.
(2)如图,连接BD.
∵∠BAD=∠DOP,∴tan∠BAD=tan∠DOP=2.
在Rt△DOP中,tan∠DOP==2,∴DP=2OD.
∵AD=2OD,∴DP=AD.
∵PD与☉O相切于点D,∴∠ADP=90°.
∴∠DPA=∠DAP=45°.
∵PA=4,∴AD=AP·sin∠DPA=4.
∵AD是☉O的直径,∴∠ABD=90°.
∴tan∠BAD==2,∴BD=2AB.
∵AB2+BD2=AD2,∴AB2+4AB2=16.
∴AB= 或AB=- (舍去).
∴线段AB的长为 .
素养探究全练
10.解析如图,过点D作DG⊥BC于点G,延长CO,交DA的延长线于点H.
∵AM,BN是☉O的两条切线,DE与☉O相切于点E,
∴AD=DE,BC=CE,∠DAB=∠ABC=90°.
∵DG⊥BC,∴四边形ABGD为矩形.
∴AD=BG,AB=DG=8.
在Rt△DGC中,CD=10,
∴GC===6.
∵CD=DE+CE=AD+BC=10,
∴AD+BG+GC=10,∴AD=BG=2,∴BC=CG+BG=8.
∵∠DAB+∠ABC=180°,∴AD∥BC.
∴∠AHO=∠BCO,∠HAO=∠CBO.
∵OA=OB,∴△HAO≌△CBO.∴AH=BC=8.
∵AD=2,∴DH=AH+AD=10.
在Rt△ABD中,AD=2,AB=8,
∴BD===2,
∵AD∥BC,∴△DHF∽△BCF.∴=,
即=,解得BF=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
