5.8 正多边形和圆课时练(含解析)
文档属性
| 名称 | 5.8 正多边形和圆课时练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 555.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:36:54 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
圆
8 正多边形和圆
基础过关全练
知识点1 正多边形的画法
1.尺规作图具有特殊的魅力.传说拿破仑通过下列尺规作图考他的大臣(如图所示):
①将半径为r的☉O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC的长为半径画弧,G是两弧的一个交点;
③连接OG.
问:OG的长是多少 大臣给出的正确答案应是( )
A.r B.r C.r D.r
2.【数学文化】(2023甘肃武威中考)1672年,丹麦数学家莫尔在他的著作《欧几里得作图》中指出:只用圆规可以完成一切尺规作图.1797年,意大利数学家马斯凯罗尼又独立发现此结论,并写在他的著作《圆规的几何学》中.请你利用数学家们发现的结论,完成下面的作图题:
如图,已知☉O,A是☉O上一点,只用圆规将☉O的圆周四等分.(按如下步骤完成,保留作图痕迹)
①以点A为圆心,OA长为半径,自点A起,在☉O上逆时针方向顺次截取==;
②分别以点A,点D为圆心,AC长为半径作弧,两弧交于☉O上方点E;
③以点A为圆心,OE长为半径作弧交☉O于G,H两点.则点A,G,D,H将☉O的圆周四等分.
3.如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
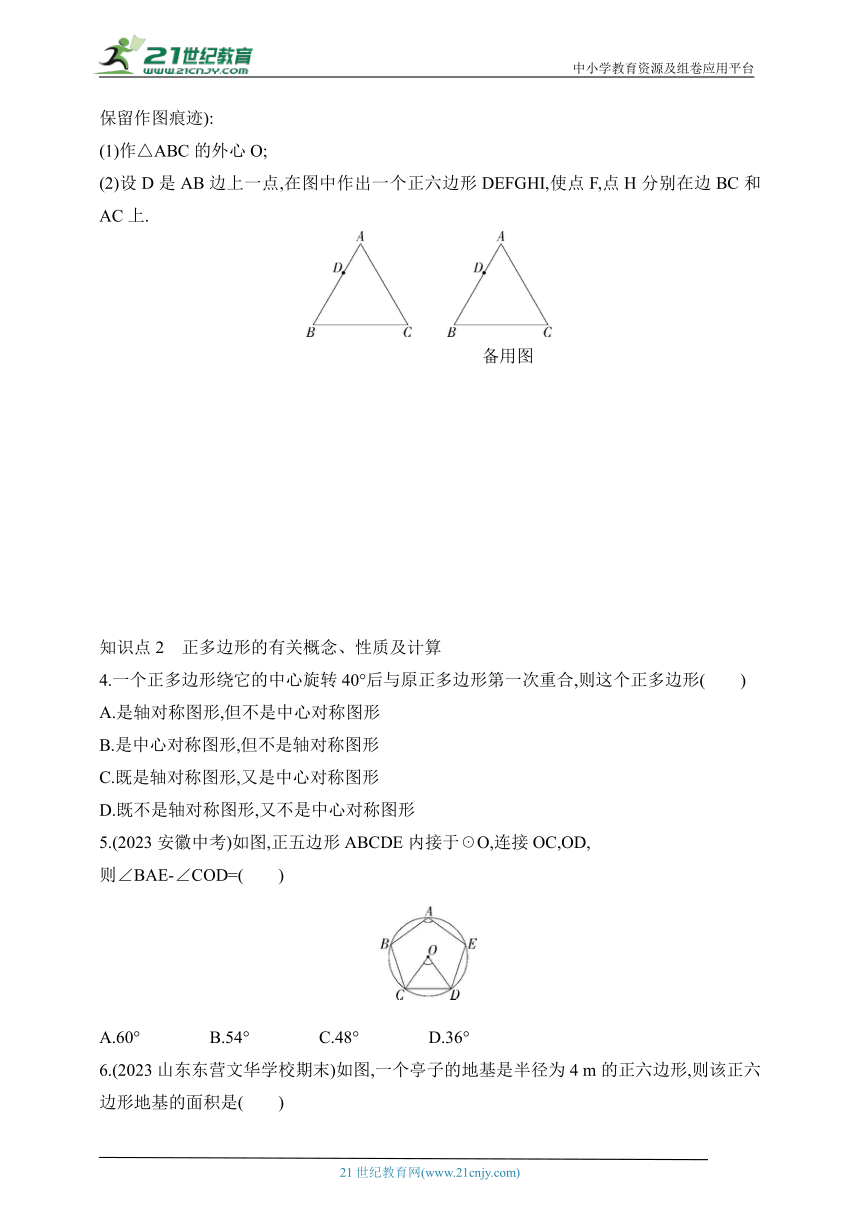
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.
备用图
知识点2 正多边形的有关概念、性质及计算
4.一个正多边形绕它的中心旋转40°后与原正多边形第一次重合,则这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
5.(2023安徽中考)如图,正五边形ABCDE内接于☉O,连接OC,OD,
则∠BAE-∠COD=( )
A.60° B.54° C.48° D.36°
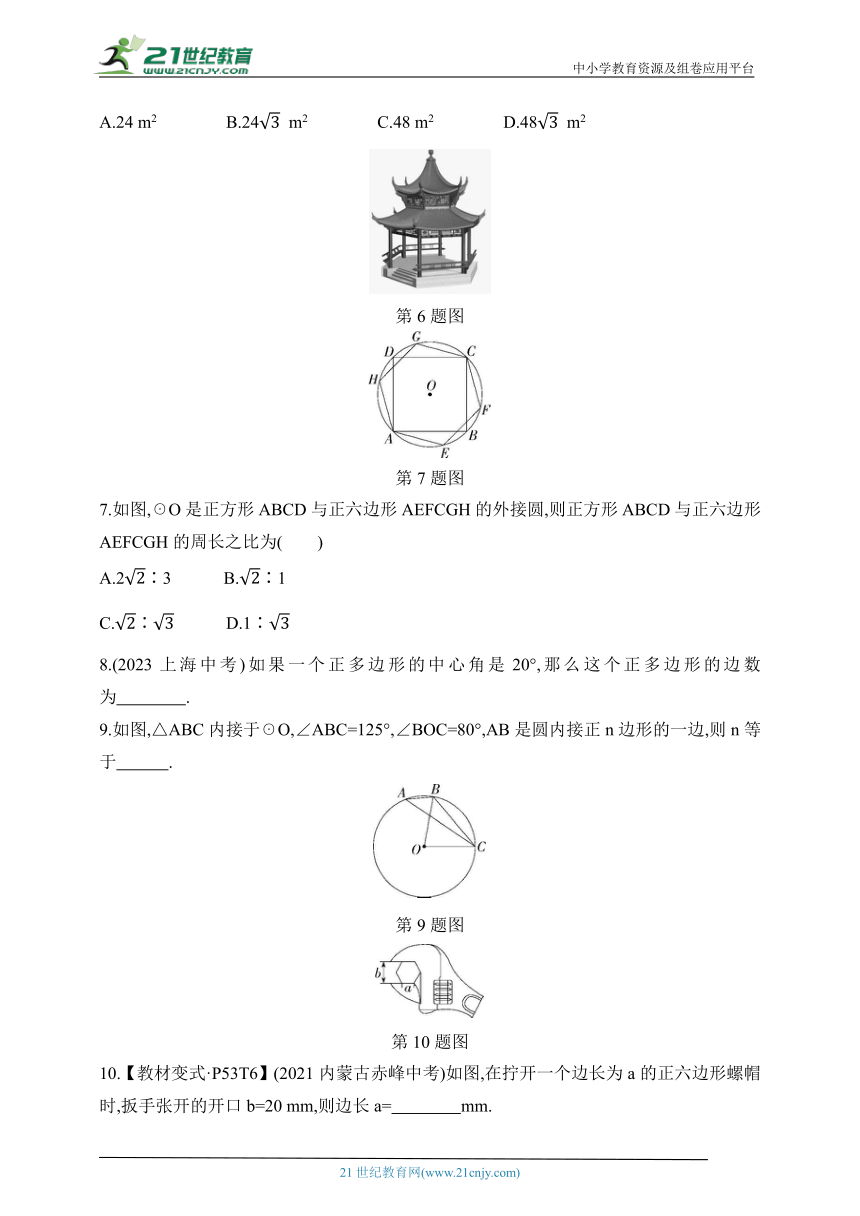
6.(2023山东东营文华学校期末)如图,一个亭子的地基是半径为4 m的正六边形,则该正六边形地基的面积是( )
A.24 m2 B.24 m2 C.48 m2 D.48 m2
第6题图
第7题图
7.如图,☉O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2∶3 B.∶1
C.∶ D.1∶
8.(2023上海中考)如果一个正多边形的中心角是20°,那么这个正多边形的边数为 .
9.如图,△ABC内接于☉O,∠ABC=125°,∠BOC=80°,AB是圆内接正n边形的一边,则n等于 .
第9题图
第10题图
10.【教材变式·P53T6】(2021内蒙古赤峰中考)如图,在拧开一个边长为a的正六边形螺帽时,扳手张开的开口b=20 mm,则边长a= mm.
11.(2021河北中考)如图,☉O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1~12的整数),过点A7作☉O的切线交A1A11的延长线于点P.
(1)连接A7A11,则A7A11和PA1有什么特殊位置关系 请简要说明理由;
(2)求PA7的长.
能力提升全练
12.【数学文化】(2023福建中考,10,★★☆)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,☉O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计☉O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为( )
A. B.2 C.3 D.2
13.【构造法】(2020四川凉山州中考,11,★★☆)如图,等边三角形ABC和正方形ADEF都内接于☉O,则AD∶AB=( )
A.2∶ B.∶ C.∶ D.∶2
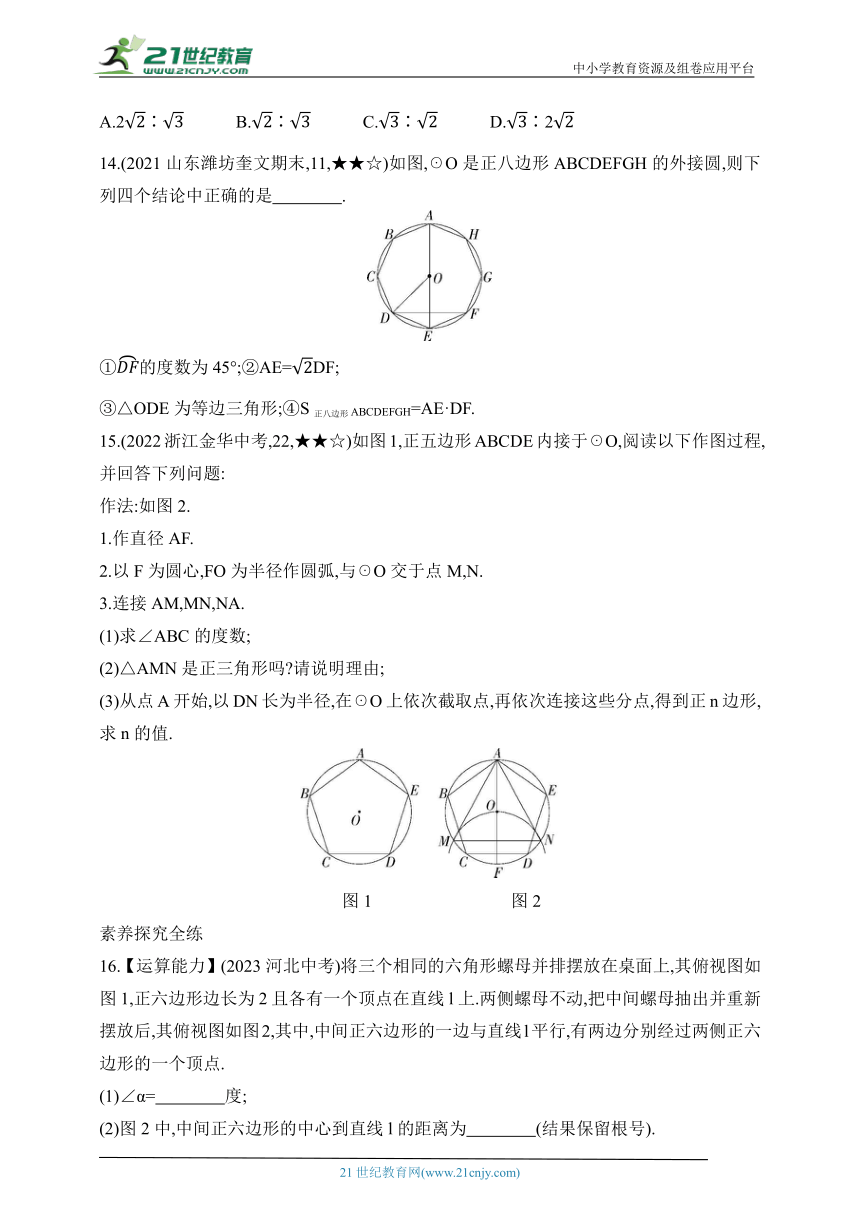
14.(2021山东潍坊奎文期末,11,★★☆)如图,☉O是正八边形ABCDEFGH的外接圆,则下列四个结论中正确的是 .
①的度数为45°;②AE=DF;
③△ODE为等边三角形;④S正八边形ABCDEFGH=AE·DF.
15.(2022浙江金华中考,22,★★☆)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:
作法:如图2.
1.作直径AF.
2.以F为圆心,FO为半径作圆弧,与☉O交于点M,N.
3.连接AM,MN,NA.
(1)求∠ABC的度数;
(2)△AMN是正三角形吗 请说明理由;
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
素养探究全练
16.【运算能力】(2023河北中考)将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.
(1)∠α= 度;
(2)图2中,中间正六边形的中心到直线l的距离为 (结果保留根号).
图1 图2
答案全解全析
基础过关全练
1.D 如图,连接CD,AC,DG,AG.
∵AD是☉O的直径,∴∠ACD=90°.
在Rt△ACD中,AD=2r,∠DAC=30°,∴AC=r.
由题意得直线OG为线段AD的垂直平分线,且DG=AG=AC=r,OD=OA=r,
∴OG⊥AD.∴∠GOA=90°.∴OG===r.故选D.
2.解析如图,
点A,G,D,H将☉O的圆周四等分.
3.解析(1)如图所示,点O即为所求.
(2)分别在△ABC的三边上截取BF=CH=AD,得等边△DFH;再作△DFH三边的垂直平分线,确定△DFH的外心O;最后作△DFH的外接圆,与△DFH三边的垂直平分线分别交于点E、G、I,顺次连接D、E、F、G、H、I、D.如图所示,六边形DEFGHI即为所求作的正六边形.(作图方法不唯一)
4.A ∵=9,∴这个正多边形是正九边形,它是轴对称图形,但不是中心对称图形.
5.D ∵五边形ABCDE是正五边形,
∴∠BAE==108°,∠COD==72°.
∴∠BAE-∠COD=108°-72°=36°,故选D.
6.B 下图是正六边形地基的草图,点O是中心,连接OB,OC,过O作OM⊥BC于M,则OB=OC=4 m.
∵六边形ABCDEF是正六边形,
∴∠BOC==60°.
∵OB=OC,∴△OBC是等边三角形.
∴∠BCO=60°,BC=CO=BO=4 m,
∴OM=OC·sin∠BCO=4×sin 60°=2(m).
∴S△OBC=BC·OM=×4×2=4(m2).
∴S正六边形ABCDEF=6S△OBC=24 m2.故选B.
7.A 设☉O的半径为r,则正方形ABCD的边长为r,正六边形AEFCGH的边长为r,所以正方形ABCD的周长与正六边形AEFCGH的周长之比为4r∶6r=2∶3.故选A.
8.答案18
解析360°÷20°=18,故这个正多边形的边数为18.
9.答案12
解析如图,连接AO.
∵∠BAC=∠BOC,∠BOC=80°,∴∠BAC=×80°=40°.
∵∠ABC=125°,∴∠ACB=180°-∠BAC-∠ABC=15°.∴∠AOB=30°.
∵AB是圆内接正n边形的一边,∴n==12.
10.答案
解析如图,设点O为正六边形ABCDEF的中心,连接OC,OD,过O作OH⊥CD于H.
则∠COD==60°,
∵OC=OD,∴∠COH=∠COD=30°,CH=DH=CD,∵OH=b=×20=10(mm),
∴CH=10×tan 30°=(mm),
∴a=2CH= mm.
11.解析(1)PA1⊥A7A11.理由:如图,连接A1A7,
易知A1A7是☉O的直径,∴∠A7A11A1=90°.
∴PA1⊥A7A11.
(2)∵直线PA7是☉O的切线,∴PA7⊥A1A7.∴∠PA7A1=90°.如图,连接OA11,由题意知∠PA1A7=∠A7OA11=60°,A1A7=12,∴PA7=A1A7·tan 60°=12.
能力提升全练
12.C 如图,AB是正十二边形的一条边,点O是正十二边形的中心,OA、OB是正十二边形的半径,设OA=OB=1,过A作AM⊥OB于M.
在正十二边形中,∠AOB=360°÷12=30°,
∴AM=OA=.∴S△AOB=OB·AM=×1×=.
∴正十二边形的面积为12×=3.
∴3≈12×π,∴π≈3.
∴π的近似值为3,故选C.
13.B 如图,连接OA,OB,OD,过O作OH⊥AB于H,则AH=BH=AB.
∵正方形ADEF和等边三角形ABC都内接于☉O,
∴∠AOB=120°,∠AOD=90°.
∵OA=OD=OB,∴△AOD是等腰直角三角形,
∠AOH=∠BOH=×120°=60°.
∴AD=OA,AH=OA·sin 60°=OA.
∴AB=2AH=2×OA=OA.
∴==.故选B.
14.答案②④
解析连接OF(图略).∵∠DOE=∠EOF==45°,∴∠DOF=90°.∴的度数为90°.故①错误.
∵∠DOF=90°,OD=OF,∴OD=DF.∵AE=2OD,
∴AE=DF.故②正确.∵∠DOE=45°,∴△ODE不可能为等边三角形,故③错误.
∵S四边形ODEF=DF·OE,∴S正八边形ABCDEFGH=4S四边形ODEF=2DF·OE.∵OE=AE,
∴S正八边形ABCDEFGH=AE·DF,故④正确.
15.解析(1)∵五边形ABCDE为正五边形,
∴∠ABC==108°.
(2)△AMN是正三角形.理由如下:
如图,连接ON,FN,由作图知FN=FO.
∵ON=OF,∴ON=OF=FN,
∴△OFN是正三角形,
∴∠OFN=60°,∴∠AMN=∠OFN=60°.
同理可得,∠ANM=60°,
∴∠MAN=60°,∴△AMN是正三角形.
(3)∵的度数=2∠AMN=120°,
的度数=2的度数=2×=144°,
∴的度数=的度数-的度数=144°-120°=24°,
∴n==15.
素养探究全练
16.答案(1)30 (2)2
解析(1)如图所示,
∵多边形是正六边形,∴∠ACB==60°.
∵BC∥直线l,∴∠ABC=90°.∴∠α=90°-60°=30°.
(2)设中间正六边形的中心为O,如图所示.
由题意得BC=FH.
在Rt△PDE中, ∠PDE=∠ACB=60°,
∴∠DPE=30°,∴DE=1,PE=.
由题图1知AG=BF=2PE=2,OM=PE=.
∴BC=(BF-CH)=×(2-2)=-1,
∴AB===3-.
∴BD=2-AB=-1.∴BE=BD+DE=.
∴ON=OM+MN=OM+BE=2.
∴中间正六边形的中心到直线l的距离为2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
圆
8 正多边形和圆
基础过关全练
知识点1 正多边形的画法
1.尺规作图具有特殊的魅力.传说拿破仑通过下列尺规作图考他的大臣(如图所示):
①将半径为r的☉O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC的长为半径画弧,G是两弧的一个交点;
③连接OG.
问:OG的长是多少 大臣给出的正确答案应是( )
A.r B.r C.r D.r
2.【数学文化】(2023甘肃武威中考)1672年,丹麦数学家莫尔在他的著作《欧几里得作图》中指出:只用圆规可以完成一切尺规作图.1797年,意大利数学家马斯凯罗尼又独立发现此结论,并写在他的著作《圆规的几何学》中.请你利用数学家们发现的结论,完成下面的作图题:
如图,已知☉O,A是☉O上一点,只用圆规将☉O的圆周四等分.(按如下步骤完成,保留作图痕迹)
①以点A为圆心,OA长为半径,自点A起,在☉O上逆时针方向顺次截取==;
②分别以点A,点D为圆心,AC长为半径作弧,两弧交于☉O上方点E;
③以点A为圆心,OE长为半径作弧交☉O于G,H两点.则点A,G,D,H将☉O的圆周四等分.
3.如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.
备用图
知识点2 正多边形的有关概念、性质及计算
4.一个正多边形绕它的中心旋转40°后与原正多边形第一次重合,则这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
5.(2023安徽中考)如图,正五边形ABCDE内接于☉O,连接OC,OD,
则∠BAE-∠COD=( )
A.60° B.54° C.48° D.36°
6.(2023山东东营文华学校期末)如图,一个亭子的地基是半径为4 m的正六边形,则该正六边形地基的面积是( )
A.24 m2 B.24 m2 C.48 m2 D.48 m2
第6题图
第7题图
7.如图,☉O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2∶3 B.∶1
C.∶ D.1∶
8.(2023上海中考)如果一个正多边形的中心角是20°,那么这个正多边形的边数为 .
9.如图,△ABC内接于☉O,∠ABC=125°,∠BOC=80°,AB是圆内接正n边形的一边,则n等于 .
第9题图
第10题图
10.【教材变式·P53T6】(2021内蒙古赤峰中考)如图,在拧开一个边长为a的正六边形螺帽时,扳手张开的开口b=20 mm,则边长a= mm.
11.(2021河北中考)如图,☉O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1~12的整数),过点A7作☉O的切线交A1A11的延长线于点P.
(1)连接A7A11,则A7A11和PA1有什么特殊位置关系 请简要说明理由;
(2)求PA7的长.
能力提升全练
12.【数学文化】(2023福建中考,10,★★☆)我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.141 6.如图,☉O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计☉O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为( )
A. B.2 C.3 D.2
13.【构造法】(2020四川凉山州中考,11,★★☆)如图,等边三角形ABC和正方形ADEF都内接于☉O,则AD∶AB=( )
A.2∶ B.∶ C.∶ D.∶2
14.(2021山东潍坊奎文期末,11,★★☆)如图,☉O是正八边形ABCDEFGH的外接圆,则下列四个结论中正确的是 .
①的度数为45°;②AE=DF;
③△ODE为等边三角形;④S正八边形ABCDEFGH=AE·DF.
15.(2022浙江金华中考,22,★★☆)如图1,正五边形ABCDE内接于☉O,阅读以下作图过程,并回答下列问题:
作法:如图2.
1.作直径AF.
2.以F为圆心,FO为半径作圆弧,与☉O交于点M,N.
3.连接AM,MN,NA.
(1)求∠ABC的度数;
(2)△AMN是正三角形吗 请说明理由;
(3)从点A开始,以DN长为半径,在☉O上依次截取点,再依次连接这些分点,得到正n边形,求n的值.
图1 图2
素养探究全练
16.【运算能力】(2023河北中考)将三个相同的六角形螺母并排摆放在桌面上,其俯视图如图1,正六边形边长为2且各有一个顶点在直线l上.两侧螺母不动,把中间螺母抽出并重新摆放后,其俯视图如图2,其中,中间正六边形的一边与直线l平行,有两边分别经过两侧正六边形的一个顶点.
(1)∠α= 度;
(2)图2中,中间正六边形的中心到直线l的距离为 (结果保留根号).
图1 图2
答案全解全析
基础过关全练
1.D 如图,连接CD,AC,DG,AG.
∵AD是☉O的直径,∴∠ACD=90°.
在Rt△ACD中,AD=2r,∠DAC=30°,∴AC=r.
由题意得直线OG为线段AD的垂直平分线,且DG=AG=AC=r,OD=OA=r,
∴OG⊥AD.∴∠GOA=90°.∴OG===r.故选D.
2.解析如图,
点A,G,D,H将☉O的圆周四等分.
3.解析(1)如图所示,点O即为所求.
(2)分别在△ABC的三边上截取BF=CH=AD,得等边△DFH;再作△DFH三边的垂直平分线,确定△DFH的外心O;最后作△DFH的外接圆,与△DFH三边的垂直平分线分别交于点E、G、I,顺次连接D、E、F、G、H、I、D.如图所示,六边形DEFGHI即为所求作的正六边形.(作图方法不唯一)
4.A ∵=9,∴这个正多边形是正九边形,它是轴对称图形,但不是中心对称图形.
5.D ∵五边形ABCDE是正五边形,
∴∠BAE==108°,∠COD==72°.
∴∠BAE-∠COD=108°-72°=36°,故选D.
6.B 下图是正六边形地基的草图,点O是中心,连接OB,OC,过O作OM⊥BC于M,则OB=OC=4 m.
∵六边形ABCDEF是正六边形,
∴∠BOC==60°.
∵OB=OC,∴△OBC是等边三角形.
∴∠BCO=60°,BC=CO=BO=4 m,
∴OM=OC·sin∠BCO=4×sin 60°=2(m).
∴S△OBC=BC·OM=×4×2=4(m2).
∴S正六边形ABCDEF=6S△OBC=24 m2.故选B.
7.A 设☉O的半径为r,则正方形ABCD的边长为r,正六边形AEFCGH的边长为r,所以正方形ABCD的周长与正六边形AEFCGH的周长之比为4r∶6r=2∶3.故选A.
8.答案18
解析360°÷20°=18,故这个正多边形的边数为18.
9.答案12
解析如图,连接AO.
∵∠BAC=∠BOC,∠BOC=80°,∴∠BAC=×80°=40°.
∵∠ABC=125°,∴∠ACB=180°-∠BAC-∠ABC=15°.∴∠AOB=30°.
∵AB是圆内接正n边形的一边,∴n==12.
10.答案
解析如图,设点O为正六边形ABCDEF的中心,连接OC,OD,过O作OH⊥CD于H.
则∠COD==60°,
∵OC=OD,∴∠COH=∠COD=30°,CH=DH=CD,∵OH=b=×20=10(mm),
∴CH=10×tan 30°=(mm),
∴a=2CH= mm.
11.解析(1)PA1⊥A7A11.理由:如图,连接A1A7,
易知A1A7是☉O的直径,∴∠A7A11A1=90°.
∴PA1⊥A7A11.
(2)∵直线PA7是☉O的切线,∴PA7⊥A1A7.∴∠PA7A1=90°.如图,连接OA11,由题意知∠PA1A7=∠A7OA11=60°,A1A7=12,∴PA7=A1A7·tan 60°=12.
能力提升全练
12.C 如图,AB是正十二边形的一条边,点O是正十二边形的中心,OA、OB是正十二边形的半径,设OA=OB=1,过A作AM⊥OB于M.
在正十二边形中,∠AOB=360°÷12=30°,
∴AM=OA=.∴S△AOB=OB·AM=×1×=.
∴正十二边形的面积为12×=3.
∴3≈12×π,∴π≈3.
∴π的近似值为3,故选C.
13.B 如图,连接OA,OB,OD,过O作OH⊥AB于H,则AH=BH=AB.
∵正方形ADEF和等边三角形ABC都内接于☉O,
∴∠AOB=120°,∠AOD=90°.
∵OA=OD=OB,∴△AOD是等腰直角三角形,
∠AOH=∠BOH=×120°=60°.
∴AD=OA,AH=OA·sin 60°=OA.
∴AB=2AH=2×OA=OA.
∴==.故选B.
14.答案②④
解析连接OF(图略).∵∠DOE=∠EOF==45°,∴∠DOF=90°.∴的度数为90°.故①错误.
∵∠DOF=90°,OD=OF,∴OD=DF.∵AE=2OD,
∴AE=DF.故②正确.∵∠DOE=45°,∴△ODE不可能为等边三角形,故③错误.
∵S四边形ODEF=DF·OE,∴S正八边形ABCDEFGH=4S四边形ODEF=2DF·OE.∵OE=AE,
∴S正八边形ABCDEFGH=AE·DF,故④正确.
15.解析(1)∵五边形ABCDE为正五边形,
∴∠ABC==108°.
(2)△AMN是正三角形.理由如下:
如图,连接ON,FN,由作图知FN=FO.
∵ON=OF,∴ON=OF=FN,
∴△OFN是正三角形,
∴∠OFN=60°,∴∠AMN=∠OFN=60°.
同理可得,∠ANM=60°,
∴∠MAN=60°,∴△AMN是正三角形.
(3)∵的度数=2∠AMN=120°,
的度数=2的度数=2×=144°,
∴的度数=的度数-的度数=144°-120°=24°,
∴n==15.
素养探究全练
16.答案(1)30 (2)2
解析(1)如图所示,
∵多边形是正六边形,∴∠ACB==60°.
∵BC∥直线l,∴∠ABC=90°.∴∠α=90°-60°=30°.
(2)设中间正六边形的中心为O,如图所示.
由题意得BC=FH.
在Rt△PDE中, ∠PDE=∠ACB=60°,
∴∠DPE=30°,∴DE=1,PE=.
由题图1知AG=BF=2PE=2,OM=PE=.
∴BC=(BF-CH)=×(2-2)=-1,
∴AB===3-.
∴BD=2-AB=-1.∴BE=BD+DE=.
∴ON=OM+MN=OM+BE=2.
∴中间正六边形的中心到直线l的距离为2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
