5.10 圆锥的侧面积课时练(含解析)
文档属性
| 名称 | 5.10 圆锥的侧面积课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 387.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:38:34 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
圆
10 圆锥的侧面积
基础过关全练
知识点 圆锥的侧面积、全面积
1.(2022四川德阳中考)一个圆锥的底面直径是8,母线长是9,则圆锥侧面展开图的面积是( )
A.16π B.52π C.36π D.72π
2.(2022四川广安中考)蒙古包可以近似地看做由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2 m,圆锥的高AC=1.5 m,圆柱的高CD=2.5 m,则下列说法错误的是( )
A.圆柱的底面积为4π m2
B.圆柱的侧面积为10π m2
C.圆锥的母线长AB为2.25 m
D.圆锥的侧面积为5π m2
3.【方程思想】(2023山东东营中考)如果圆锥侧面展开图的面积是15π,母线长是5,那么这个圆锥的底面半径是( )
A.3 B.4 C.5 D.6
4.如图所示的是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,已知AB=12 cm,BC=8 cm,则这个零件的表面积是( )
A.192π cm2 B.196π cm2
C.228π cm2 D.232π cm2
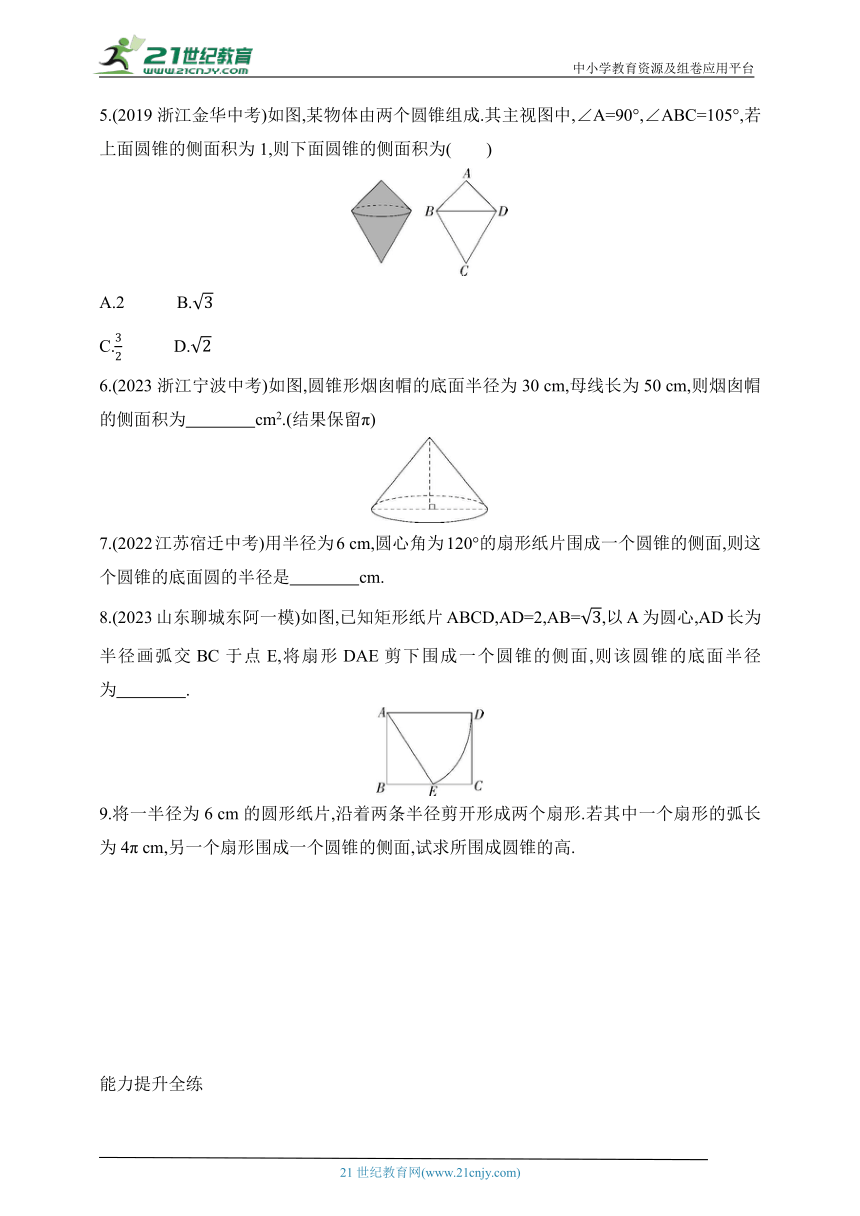
5.(2019浙江金华中考)如图,某物体由两个圆锥组成.其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B.
C. D.
6.(2023浙江宁波中考)如图,圆锥形烟囱帽的底面半径为30 cm,母线长为50 cm,则烟囱帽的侧面积为 cm2.(结果保留π)
7.(2022江苏宿迁中考)用半径为6 cm,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径是 cm.
8.(2023山东聊城东阿一模)如图,已知矩形纸片ABCD,AD=2,AB=,以A为圆心,AD长为半径画弧交BC于点E,将扇形DAE剪下围成一个圆锥的侧面,则该圆锥的底面半径为 .
9.将一半径为6 cm的圆形纸片,沿着两条半径剪开形成两个扇形.若其中一个扇形的弧长为4π cm,另一个扇形围成一个圆锥的侧面,试求所围成圆锥的高.
能力提升全练
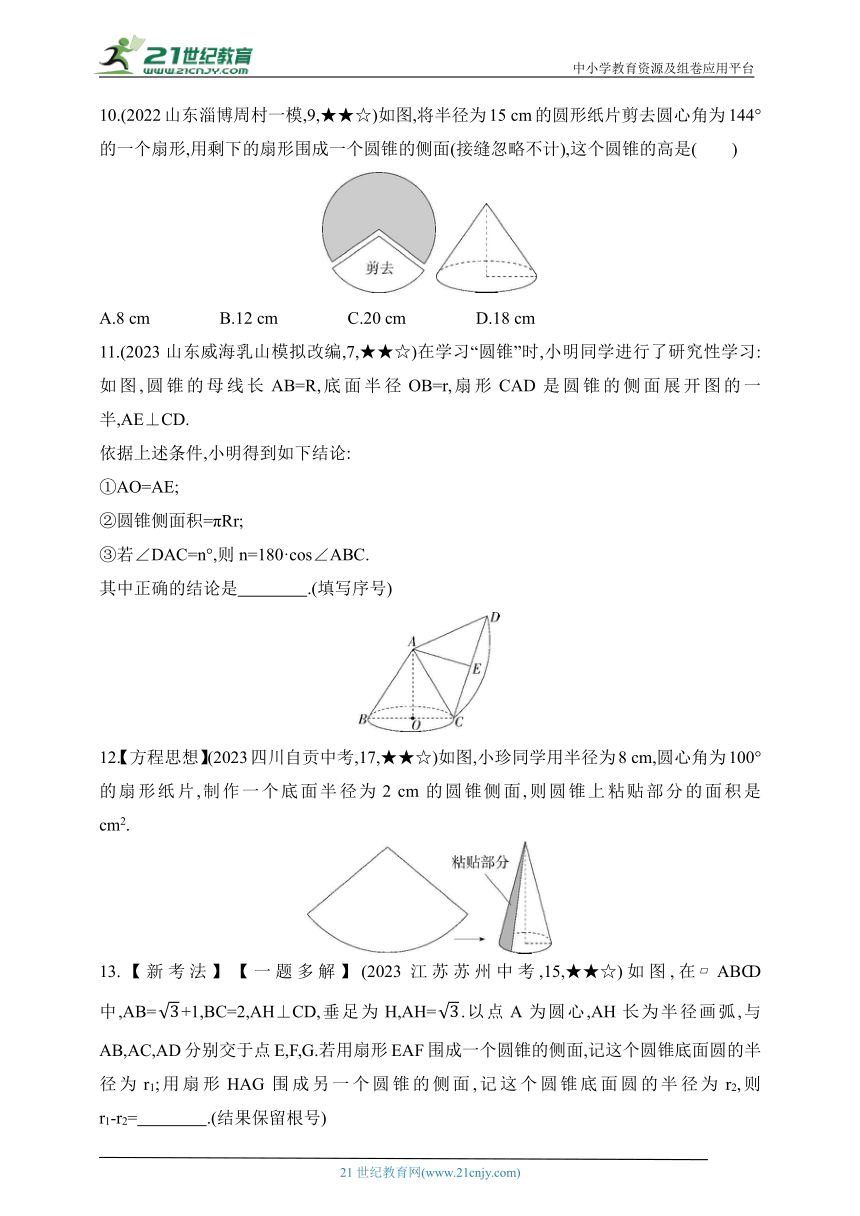
10.(2022山东淄博周村一模,9,★★☆)如图,将半径为15 cm的圆形纸片剪去圆心角为144°的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
A.8 cm B.12 cm C.20 cm D.18 cm
11.(2023山东威海乳山模拟改编,7,★★☆)在学习“圆锥”时,小明同学进行了研究性学习:如图,圆锥的母线长AB=R,底面半径OB=r,扇形CAD是圆锥的侧面展开图的一半,AE⊥CD.
依据上述条件,小明得到如下结论:
①AO=AE;
②圆锥侧面积=πRr;
③若∠DAC=n°,则n=180·cos∠ABC.
其中正确的结论是 .(填写序号)
12.【方程思想】(2023四川自贡中考,17,★★☆)如图,小珍同学用半径为8 cm,圆心角为100°的扇形纸片,制作一个底面半径为2 cm的圆锥侧面,则圆锥上粘贴部分的面积是 cm2.
13.【新考法】【一题多解】(2023江苏苏州中考,15,★★☆)如图,在 ABCD中,AB=+1,BC=2,AH⊥CD,垂足为H,AH=.以点A为圆心,AH长为半径画弧,与AB,AC,AD分别交于点E,F,G.若用扇形EAF围成一个圆锥的侧面,记这个圆锥底面圆的半径为r1;用扇形HAG围成另一个圆锥的侧面,记这个圆锥底面圆的半径为r2,则r1-r2= .(结果保留根号)
素养探究全练
14.【教材变式·P59T5】(2023湖北十堰中考)如图,已知点C为圆锥母线SB的中点,AB为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为( )
A.5 B.3 C.3 D.6
第五章 圆
10 圆锥的侧面积
答案全解全析
基础过关全练
1.C 圆锥侧面展开图的面积为π××8×9=36π,故选C.
2.C A项,∵底面圆半径DE=2 m,∴圆柱的底面积为4π m2,
∴A选项正确,不符合题意;
B项,∵圆柱的高CD=2.5 m,
∴圆柱的侧面积=2π×2×2.5=10π(m2),∴B选项正确,不符合题意;
C项,∵底面圆半径DE=2 m,∴BC=2 m,∵圆锥的高AC=1.5 m,
∴圆锥的母线长AB==2.5(m),∴C选项错误,符合题意;
D项,圆锥的侧面积=π×2×2.5=5π(m2),∴D选项正确,不符合题意.故选C.
3.A 设底面半径为r,则πr×5=15π,∴r=3.故选A.
4.A 由题意得圆锥的底面半径为6 cm,高为8 cm,
∴圆锥的母线长为10 cm,∴圆锥的侧面积=π×6×10=60π(cm2),
∵圆柱的侧面积=12π×8=96π(cm2),圆柱的底面积=π×62=36π(cm2),
∴零件的表面积=60π+96π+36π=192π(cm2).故选A.
5.D ∵∠A=90°,AB=AD,
∴△ABD为等腰直角三角形,
∴∠ABD=45°,BD=AB,
∵∠ABC=105°,∴∠CBD=60°,
∵CB=CD,∴△CBD为等边三角形,
∴BC=BD=AB,
∵上面圆锥与下面圆锥的底面相同,
∴上面圆锥的侧面积∶下面圆锥的侧面积=AB∶CB,
∴下面圆锥的侧面积=×1=.故选D.
6.答案1 500π
解析烟囱帽的侧面积为π×30×50=1 500π(cm2).
7.答案2
解析设这个圆锥的底面圆的半径为r cm,由题意得2πr=,解得r=2.
∴这个圆锥的底面圆的半径为2 cm.
8.答案
解析由题意得cos∠BAE==,
∴∠BAE=30°.∴∠DAE=60°.
∴圆锥的侧面展开图的弧长为=π.
∴圆锥的底面半径为π÷2π=.
9.解析∵半径为6 cm的圆的周长为12π cm,
∴另一个扇形的弧长为12π-4π=8π(cm).
∴所围成圆锥的底面圆半径为8π÷2π=4(cm).
∴所围成圆锥的高为=2(cm).
能力提升全练
10.B 设圆锥的底面圆的半径为r cm,
根据题意得2πr=,解得r=9.
∴圆锥的高==12(cm).故选B.
11.答案②③
解析①易知∠BAC<∠CAD,∴∠OAC<∠CAE,在Rt△AOC和Rt△ACE中,
AO=AC·cos∠OAC,AE=AC·cos∠CAE,∵cos∠OAC>cos∠CAE,∴AO>AE,∴①不正确;
②由圆锥的侧面积公式知②正确;
③∵2πr=,∴n=×180.
在Rt△ABO中,cos∠ABO==,
∴n=180·cos∠ABO,∴③正确.
故填②③.
12.答案
解析设圆锥侧面展开图的圆心角为n°,
则2π×2=,解得n=90.
∴粘贴部分所对应的圆心角为100°-90°=10°.
∴圆锥上粘贴部分的面积是=(cm2).
13.答案
解析此题综合平行四边形的知识考查圆锥的计算,设题新颖.
解法一:在 ABCD中,AB=+1,BC=2,
∴AD=BC=2,CD=AB=+1,AB∥CD.
∵AH⊥CD,AH=,∴sin D==.∴∠D=60°.
∴∠DAH=90°-∠D=30°.∴DH=AD=1.
∴CH=CD-DH=+1-1=.
∴CH=AH.∵AH⊥CD,∴△ACH是等腰直角三角形.
∴∠ACH=∠CAH=45°.
∵AB∥CD,∴∠BAC=∠ACH=45°.
∴=2πr1,解得r1=,
=2πr2,解得r2=.
∴r1-r2=-=.
解法二(整体求解):
由解法一知∠BAC=45°,∠DAH=30°,
∴πr1·-πr2·=-=,∴r1-r2=.
素养探究全练
14.B 将圆锥的侧面展开,如图,连接AB,AC.
易知线段AC的长度为蚂蚁爬行的最短路程.
由题意知,底面圆的直径=4,∴底面周长=4π.
设圆锥的侧面展开图的圆心角为n°,
则4π=,解得n=120.
∴展开图中∠ASB=120°÷2=60°.
又∵SA=SB,∴△SAB为等边三角形.
又∵C为SB的中点,∴AC⊥SB.
∴AC=AS·sin∠ASB=6·sin 60°=3.
∴蚂蚁爬行的最短路程为3.故选B.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
圆
10 圆锥的侧面积
基础过关全练
知识点 圆锥的侧面积、全面积
1.(2022四川德阳中考)一个圆锥的底面直径是8,母线长是9,则圆锥侧面展开图的面积是( )
A.16π B.52π C.36π D.72π
2.(2022四川广安中考)蒙古包可以近似地看做由圆锥和圆柱组成.下图是一个蒙古包的示意图,底面圆半径DE=2 m,圆锥的高AC=1.5 m,圆柱的高CD=2.5 m,则下列说法错误的是( )
A.圆柱的底面积为4π m2
B.圆柱的侧面积为10π m2
C.圆锥的母线长AB为2.25 m
D.圆锥的侧面积为5π m2
3.【方程思想】(2023山东东营中考)如果圆锥侧面展开图的面积是15π,母线长是5,那么这个圆锥的底面半径是( )
A.3 B.4 C.5 D.6
4.如图所示的是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,已知AB=12 cm,BC=8 cm,则这个零件的表面积是( )
A.192π cm2 B.196π cm2
C.228π cm2 D.232π cm2
5.(2019浙江金华中考)如图,某物体由两个圆锥组成.其主视图中,∠A=90°,∠ABC=105°,若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B.
C. D.
6.(2023浙江宁波中考)如图,圆锥形烟囱帽的底面半径为30 cm,母线长为50 cm,则烟囱帽的侧面积为 cm2.(结果保留π)
7.(2022江苏宿迁中考)用半径为6 cm,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径是 cm.
8.(2023山东聊城东阿一模)如图,已知矩形纸片ABCD,AD=2,AB=,以A为圆心,AD长为半径画弧交BC于点E,将扇形DAE剪下围成一个圆锥的侧面,则该圆锥的底面半径为 .
9.将一半径为6 cm的圆形纸片,沿着两条半径剪开形成两个扇形.若其中一个扇形的弧长为4π cm,另一个扇形围成一个圆锥的侧面,试求所围成圆锥的高.
能力提升全练
10.(2022山东淄博周村一模,9,★★☆)如图,将半径为15 cm的圆形纸片剪去圆心角为144°的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
A.8 cm B.12 cm C.20 cm D.18 cm
11.(2023山东威海乳山模拟改编,7,★★☆)在学习“圆锥”时,小明同学进行了研究性学习:如图,圆锥的母线长AB=R,底面半径OB=r,扇形CAD是圆锥的侧面展开图的一半,AE⊥CD.
依据上述条件,小明得到如下结论:
①AO=AE;
②圆锥侧面积=πRr;
③若∠DAC=n°,则n=180·cos∠ABC.
其中正确的结论是 .(填写序号)
12.【方程思想】(2023四川自贡中考,17,★★☆)如图,小珍同学用半径为8 cm,圆心角为100°的扇形纸片,制作一个底面半径为2 cm的圆锥侧面,则圆锥上粘贴部分的面积是 cm2.
13.【新考法】【一题多解】(2023江苏苏州中考,15,★★☆)如图,在 ABCD中,AB=+1,BC=2,AH⊥CD,垂足为H,AH=.以点A为圆心,AH长为半径画弧,与AB,AC,AD分别交于点E,F,G.若用扇形EAF围成一个圆锥的侧面,记这个圆锥底面圆的半径为r1;用扇形HAG围成另一个圆锥的侧面,记这个圆锥底面圆的半径为r2,则r1-r2= .(结果保留根号)
素养探究全练
14.【教材变式·P59T5】(2023湖北十堰中考)如图,已知点C为圆锥母线SB的中点,AB为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为( )
A.5 B.3 C.3 D.6
第五章 圆
10 圆锥的侧面积
答案全解全析
基础过关全练
1.C 圆锥侧面展开图的面积为π××8×9=36π,故选C.
2.C A项,∵底面圆半径DE=2 m,∴圆柱的底面积为4π m2,
∴A选项正确,不符合题意;
B项,∵圆柱的高CD=2.5 m,
∴圆柱的侧面积=2π×2×2.5=10π(m2),∴B选项正确,不符合题意;
C项,∵底面圆半径DE=2 m,∴BC=2 m,∵圆锥的高AC=1.5 m,
∴圆锥的母线长AB==2.5(m),∴C选项错误,符合题意;
D项,圆锥的侧面积=π×2×2.5=5π(m2),∴D选项正确,不符合题意.故选C.
3.A 设底面半径为r,则πr×5=15π,∴r=3.故选A.
4.A 由题意得圆锥的底面半径为6 cm,高为8 cm,
∴圆锥的母线长为10 cm,∴圆锥的侧面积=π×6×10=60π(cm2),
∵圆柱的侧面积=12π×8=96π(cm2),圆柱的底面积=π×62=36π(cm2),
∴零件的表面积=60π+96π+36π=192π(cm2).故选A.
5.D ∵∠A=90°,AB=AD,
∴△ABD为等腰直角三角形,
∴∠ABD=45°,BD=AB,
∵∠ABC=105°,∴∠CBD=60°,
∵CB=CD,∴△CBD为等边三角形,
∴BC=BD=AB,
∵上面圆锥与下面圆锥的底面相同,
∴上面圆锥的侧面积∶下面圆锥的侧面积=AB∶CB,
∴下面圆锥的侧面积=×1=.故选D.
6.答案1 500π
解析烟囱帽的侧面积为π×30×50=1 500π(cm2).
7.答案2
解析设这个圆锥的底面圆的半径为r cm,由题意得2πr=,解得r=2.
∴这个圆锥的底面圆的半径为2 cm.
8.答案
解析由题意得cos∠BAE==,
∴∠BAE=30°.∴∠DAE=60°.
∴圆锥的侧面展开图的弧长为=π.
∴圆锥的底面半径为π÷2π=.
9.解析∵半径为6 cm的圆的周长为12π cm,
∴另一个扇形的弧长为12π-4π=8π(cm).
∴所围成圆锥的底面圆半径为8π÷2π=4(cm).
∴所围成圆锥的高为=2(cm).
能力提升全练
10.B 设圆锥的底面圆的半径为r cm,
根据题意得2πr=,解得r=9.
∴圆锥的高==12(cm).故选B.
11.答案②③
解析①易知∠BAC<∠CAD,∴∠OAC<∠CAE,在Rt△AOC和Rt△ACE中,
AO=AC·cos∠OAC,AE=AC·cos∠CAE,∵cos∠OAC>cos∠CAE,∴AO>AE,∴①不正确;
②由圆锥的侧面积公式知②正确;
③∵2πr=,∴n=×180.
在Rt△ABO中,cos∠ABO==,
∴n=180·cos∠ABO,∴③正确.
故填②③.
12.答案
解析设圆锥侧面展开图的圆心角为n°,
则2π×2=,解得n=90.
∴粘贴部分所对应的圆心角为100°-90°=10°.
∴圆锥上粘贴部分的面积是=(cm2).
13.答案
解析此题综合平行四边形的知识考查圆锥的计算,设题新颖.
解法一:在 ABCD中,AB=+1,BC=2,
∴AD=BC=2,CD=AB=+1,AB∥CD.
∵AH⊥CD,AH=,∴sin D==.∴∠D=60°.
∴∠DAH=90°-∠D=30°.∴DH=AD=1.
∴CH=CD-DH=+1-1=.
∴CH=AH.∵AH⊥CD,∴△ACH是等腰直角三角形.
∴∠ACH=∠CAH=45°.
∵AB∥CD,∴∠BAC=∠ACH=45°.
∴=2πr1,解得r1=,
=2πr2,解得r2=.
∴r1-r2=-=.
解法二(整体求解):
由解法一知∠BAC=45°,∠DAH=30°,
∴πr1·-πr2·=-=,∴r1-r2=.
素养探究全练
14.B 将圆锥的侧面展开,如图,连接AB,AC.
易知线段AC的长度为蚂蚁爬行的最短路程.
由题意知,底面圆的直径=4,∴底面周长=4π.
设圆锥的侧面展开图的圆心角为n°,
则4π=,解得n=120.
∴展开图中∠ASB=120°÷2=60°.
又∵SA=SB,∴△SAB为等边三角形.
又∵C为SB的中点,∴AC⊥SB.
∴AC=AS·sin∠ASB=6·sin 60°=3.
∴蚂蚁爬行的最短路程为3.故选B.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
