第六章 对概率的进一步认识素养综合检测试题(含解析)
文档属性
| 名称 | 第六章 对概率的进一步认识素养综合检测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 542.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:39:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
第六章 对概率的进一步认识
第六章 素养综合检测
满分100分,限时60分钟
一、选择题(每小题4分,共32分)
1.(2021湖南郴州中考)下列说法正确的是( )
A.“明天下雨的概率为80%”,意味着明天有80%的时间下雨
B.经过有信号灯的十字路口时,可能遇到红灯,也可能遇到绿灯
C.“某彩票中奖概率是1%”,表示买100张这种彩票一定会有1张中奖
D.因为小明前几次的数学测试成绩都在90分以上,所以这次数学测试成绩也一定在90分以上
2.【中华优秀传统文化】(2023山东东营中考)剪纸是中国最古老的民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.小文购买了以“剪纸图案”为主题的5张书签(如图),他想送给好朋友小乐一张.小文将书签背面朝上(背面完全相同),让小乐从中随机抽取一张,则小乐抽到的书签图案既是轴对称图形又是中心对称图形的概率是( )
A. B.
C. D.
3.(2023山东济南莱芜模拟)某校举行“中国品牌”运动会,小军和小雪分别从甲、乙、丙三种品牌中选一种做运动会“班牌”,他们都选到同一品牌的概率是( )
A. B.
C. D.
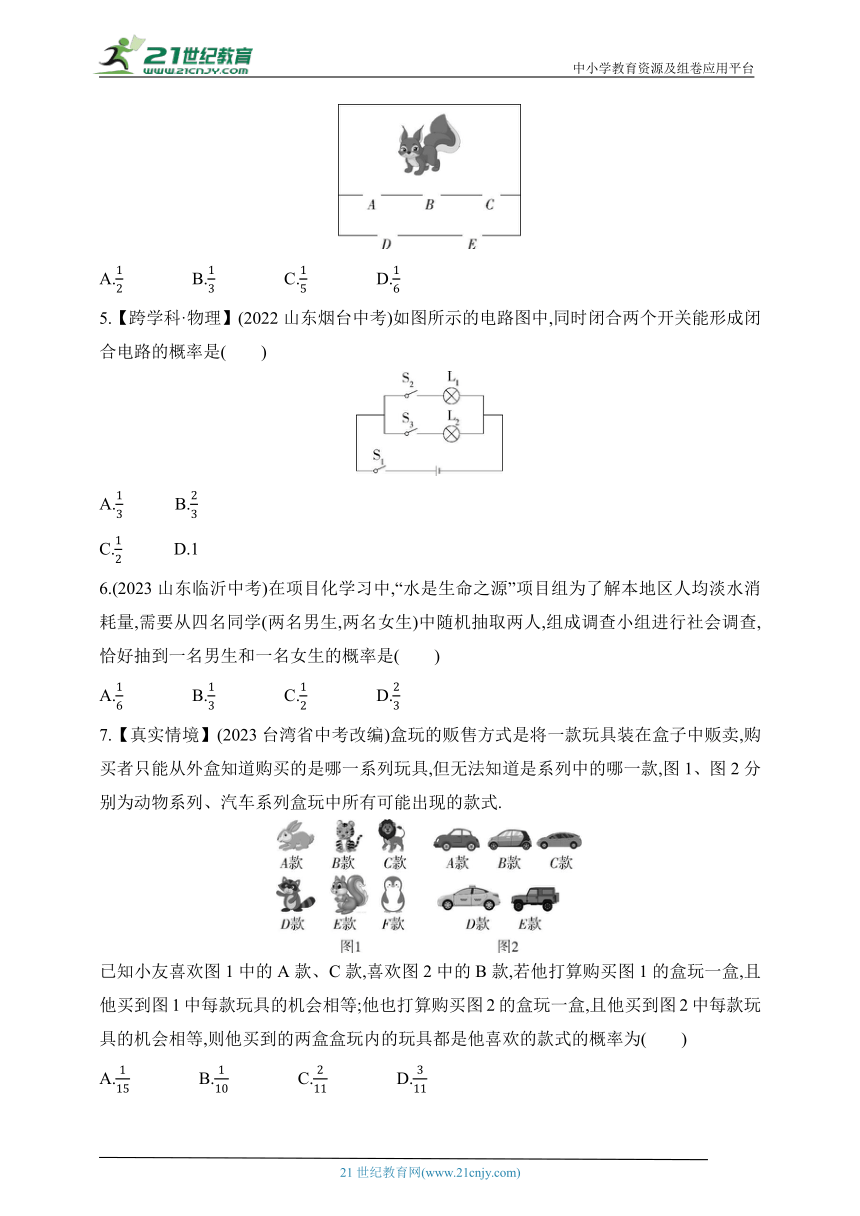
4.【新考法】(2023山东临沂罗庄二模)如图,一只松鼠先经过第一道门(A,B或C),再经过第二道门(D或E)出去,则松鼠走出笼子的路线是“先经过A门,再经过E门”的概率是( )
A. B. C. D.
5.【跨学科·物理】(2022山东烟台中考)如图所示的电路图中,同时闭合两个开关能形成闭合电路的概率是( )
A. B.
C. D.1
6.(2023山东临沂中考)在项目化学习中,“水是生命之源”项目组为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是( )
A. B. C. D.
7.【真实情境】(2023台湾省中考改编)盒玩的贩售方式是将一款玩具装在盒子中贩卖,购买者只能从外盒知道购买的是哪一系列玩具,但无法知道是系列中的哪一款,图1、图2分别为动物系列、汽车系列盒玩中所有可能出现的款式.
已知小友喜欢图1中的A款、C款,喜欢图2中的B款,若他打算购买图1的盒玩一盒,且他买到图1中每款玩具的机会相等;他也打算购买图2的盒玩一盒,且他买到图2中每款玩具的机会相等,则他买到的两盒盒玩内的玩具都是他喜欢的款式的概率为( )
A. B. C. D.
8.(2021山东烟台中考)连接正六边形不相邻的两个顶点,并将中间的六边形涂成灰色,制成如图所示的镖盘,将一枚飞镖任意投掷到镖盘上,飞镖落在阴影区域的概率为( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9.(2022山东青岛市南一模)林业部门要考察某种幼树在一定条件下的移植成活率,表格中是这种幼树在移植过程中的一组数据:
移植的棵数n 1 000 1 500 2 500 4 000
成活的棵数m 853 1 356 2 220 3 500
成活的频率 0.853 0.904 0.888 0.875
移植的棵数n 8 000 15 000 20 000 30 000
成活的棵数m 7 056 13 170 17 580 26 400
成活的频率 0.882 0.878 0.879 0.880
根据以上数据,该林业部门估计在此条件下移植的55 000棵该种幼树成活的棵数为 .
10.如图所示的是两个质地均匀的转盘,现转动转盘①和转盘②各一次,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,就能配成紫色,则能配成紫色的概率为 .
转盘①
转盘②
11.小颖从某大型商场的东门进入后,开始自由购物,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同,则经过两个十字道口后小颖向 方向参观的概率大.(填“东”“南”“西”“北”中的一个)
12.(2021内蒙古呼和浩特中考)动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此,若设刚出生的这种动物共有a只,则20年后存活的有 只,现年20岁的这种动物活到25岁的概率是 .
13.【新考法】(2023山东聊城中考)在一个不透明的袋子中,装有五个分别标有数
-,,0,2,π的小球,这些小球除标的数外其他完全相同.从袋子中随机摸出两个小球,两球上的数之积恰好是有理数的概率为 .
三、解答题(共48分)
14.[含评分细则]【真实情境】(2023山东烟台一模)(8分)如图所示的是一个迷宫示意图,小明和小亮分别从入口进入,沿着虚线所示的路线行走,两人根据自己的选择随机进入A,B,C三个房间中的某一个.
(1)小明进入A房间的概率是多少
(2)利用树状图或表格,求出两人在走迷宫结束后,B房间至少有1个人的概率.
15.[含评分细则]【新素材】(2023四川南充中考)(8分)为培养学生劳动习惯,提升学生劳动技能,某校在五月第二周开展了劳动教育实践周活动.七(1)班提供了四类活动:A.物品整理,B.环境美化,C.植物栽培,D.工具制作.要求每个学生选择其中一项活动参加,该班数学科代表对全班学生参与四类活动情况进行了统计,并绘制成统计图(如图).
(1)已知该班有15人参加A类活动,则参加C类活动的有多少人
(2)该班参加D类活动的学生中有2名女生和2名男生获得一等奖,其中一名女生叫王丽,若从获得一等奖的学生中随机抽取两人参加学校“工具制作”比赛,求刚好抽中王丽和1名男生的概率.
16.[含评分细则](10分)甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,则经过三次传球后,球传回到甲手中的概率是多少
(2)若乙想使球经过三次传递后,落在自己手中的概率最大,则乙应让球开始时在谁手中 请说明理由.
17.[含评分细则]【新独家原创】(10分)某超市在元旦期间进行购物促销活动,购物满88元即有一次抽奖机会.抽奖规则如下:一个不透明的箱子里装有若干个红色小球和1个白色小球(除颜色不同外,其他均相同),从箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球.若两次摸出的球都是白球,则中一等奖;若两次摸出的球只有一个白球,则中二等奖;若两次摸出的球没有白球,则不中奖.
(1)聪明的小卓通过观察发现每次摸到白色小球的频率稳定在0.25左右,请你估计箱子里红色小球的个数;
(2)在(1)的条件下,若小卓的妈妈有一次抽奖机会,试求小卓的妈妈中奖的概率.
18.[含评分细则]【真实情境】(2021陕西西安灞桥模拟)(12分)小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至3层的任意一层出电梯.
(1)请你用“画树状图”或“列表”的方法求甲、乙二人在同一层出电梯的概率;
(2)小亮和小芳做游戏,规则如下:若甲、乙在同一层或相邻层出电梯,则小亮胜,否则小芳胜.该游戏是否公平 请说明理由.
3层
2层
1层
地下车库
答案全解全析
1.B A项,明天下雨的概率为80%,只是说明明天下雨的可能性大,与时间无关,故本选项说法错误;B项说法正确;C项,某彩票中奖概率是1%,买100张这种彩票中奖是随机事件,不一定会有1张中奖,故本选项说法错误;D项,小明前几次的数学测试成绩都在90分以上,这次数学测试成绩不一定在90分以上,故本选项说法错误.故选B.
2.D ∵只有第二个图形既是轴对称图形又是中心对称图形,
∴小乐抽到的书签图案既是轴对称图形又是中心对称图形的概率=.
故选D.
3.B 将甲、乙、丙三种品牌分别记作A、B、C,列表如下:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
由表知,共有9种等可能的结果,其中他们都选到同一品牌的有3种结果,
所以他们都选到同一品牌的概率为=,故选B.
4.D 本题以松鼠走出笼子的路线为情境考查用列表法或画树状图法求概率.
画树状图如下:
共有6种等可能的结果,其中松鼠走出笼子的路线是“先经过A门,再经过E门”的只有1种结果,
所以松鼠走出笼子的路线是“先经过A门,再经过E门”的概率为.故选D.
5.B 把S1、S2、S3分别记为A、B、C,画树状图如下:
共有6种等可能的结果,其中同时闭合两个开关能形成闭合电路的结果有4种,即AB、AC、BA、CA,
∴同时闭合两个开关能形成闭合电路的概率为=,故选B.
6.D 画树状图如下:
共有12种等可能的结果,其中恰好抽到一名男生和一名女生的结果数为8,
所以恰好抽到一名男生和一名女生的概率==.故选D.
7.A 列表如下:
动物
系列 汽车
系列 A B C D E F
A (A,A) (B,A) (C,A) (D,A) (E,A) (F,A)
B (A,B) (B,B) (C,B) (D,B) (E,B) (F,B)
C (A,C) (B,C) (C,C) (D,C) (E,C) (F,C)
D (A,D) (B,D) (C,D) (D,D) (E,D) (F,D)
E (A,E) (B,E) (C,E) (D,E) (E,E) (F,E)
由表知,共有30种等可能的结果,其中小友买到的两盒盒玩内的玩具都是他喜欢的款式的结果有2种,
所以他买到的两盒盒玩内的玩具都是他喜欢的款式的概率为=,故选A.
8.B 添加辅助线如图所示,令S△ABC=a,
由题意可知,阴影区域为正六边形,则S阴影=6a,S大正六边形=18a,∴飞镖落在阴影区域的概率为=.故选B.
9.答案48 400
解析由题表中数据,可知幼树在移植过程中,成活的频率稳定在0.88附近,
所以估计这种幼树移植成活的概率为0.88,
则该林业部门估计在此条件下移植的55 000棵该种幼树成活的棵数为
55 000×0.88=48 400.
10.答案
解析将转盘①中红色部分等分成3部分,
画树状图如下:
由树状图可知,共有16种等可能的结果,其中能配成紫色的结果有8种,
所以能配成紫色的概率为=.
11.答案西
解析画树状图如图所示.
经过两个十字道口后,共有9种等可能的结果,其中向西的结果有3种,向东、北、南的结果都分别有2种,因此向西的概率为=,其他三个方向的概率都为,所以经过两个十字道口后小颖向西方向参观的概率大.
12.答案0.8a;
解析若刚出生的这种动物共有a只,则20年后存活的有0.8a只.设共有这种动物x只,则活到20岁的只数为0.8x,活到25岁的只数为0.5x,故现年20岁的这种动物活到25岁的概率为=.
13.答案
解析本题综合考查概率计算与实数运算.
根据题意画树状图如下:
共有20种等可能的结果,其中两球上的数之积恰好是有理数的结果有8种,
∴两球上的数字之积恰好是有理数的概率为=.
14.解析(1)共有3个房间,小明进入A房间的概率为. 2分
(2)列表如下:
小亮 小明 A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,共有9种等可能的结果,其中B房间至少有1个人的结果共有5种,
所以B房间至少有1个人的概率为. 8分
15.解析(1)该班总人数为15÷30%=50,
∴参加C类活动的有50×(1-30%-28%-22%)=50×20%=10(人). 3分
(2)把2名女生分别记为甲、乙(其中甲为王丽),2名男生分别记为丙、丁,
画树状图如下:
共有12种等可能的结果,其中刚好抽中王丽和1名男生的结果有4种,
∴刚好抽中王丽和1名男生的概率为=. 8分
16.解析(1)画树状图,如图所示:
由树状图可知,共有8种等可能的结果,经过三次传球后,球传回到甲手中的结果有2种,所以所求概率为=. 4分
(2)乙应让球开始时在甲手中或丙手中.
理由:由(1)可知,从甲开始传球,经过三次传球后,球传到甲手中的概率为,球传到乙、丙手中的概率均为,所以经过三次传球后,球回到乙手中的概率的最大值为,所以乙应让球开始时在甲手中或丙手中. 10分
17.解析(1)设红色小球有x个,
根据题意,得=0.25,解得x=3.
经检验,x=3是分式方程的解,且符合题意.
∴估计箱子里红色小球的个数为3. 3分
(2)列表如下:
红1 红2 红3 白
红1 (红1,红1) (红1,红2) (红1,红3) (红1,白)
红2 (红2,红1) (红2,红2) (红2,红3) (红2,白)
红3 (红3,红1) (红3,红2) (红3,红3) (红3,白)
白 (白,红1) (白,红2) (白,红3) (白,白)
共有16种等可能的结果,其中两次摸出的球含有白球的结果为7种,
∴小卓的妈妈中奖的概率为. 10分
18.解析(1)根据题意画树状图如下:
共有9种等可能的情况,其中甲、乙二人在同一层出电梯的情况有3种,
∴甲、乙二人在同一层出电梯的概率是=. 5分
(2)该游戏不公平.理由:9种等可能的情况中,甲、乙两人在相邻层出电梯的情况有4种,
∴小亮获胜的概率为=.
∴小芳获胜的概率为1-=.
∵>,∴该游戏不公平. 12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
第六章 对概率的进一步认识
第六章 素养综合检测
满分100分,限时60分钟
一、选择题(每小题4分,共32分)
1.(2021湖南郴州中考)下列说法正确的是( )
A.“明天下雨的概率为80%”,意味着明天有80%的时间下雨
B.经过有信号灯的十字路口时,可能遇到红灯,也可能遇到绿灯
C.“某彩票中奖概率是1%”,表示买100张这种彩票一定会有1张中奖
D.因为小明前几次的数学测试成绩都在90分以上,所以这次数学测试成绩也一定在90分以上
2.【中华优秀传统文化】(2023山东东营中考)剪纸是中国最古老的民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.小文购买了以“剪纸图案”为主题的5张书签(如图),他想送给好朋友小乐一张.小文将书签背面朝上(背面完全相同),让小乐从中随机抽取一张,则小乐抽到的书签图案既是轴对称图形又是中心对称图形的概率是( )
A. B.
C. D.
3.(2023山东济南莱芜模拟)某校举行“中国品牌”运动会,小军和小雪分别从甲、乙、丙三种品牌中选一种做运动会“班牌”,他们都选到同一品牌的概率是( )
A. B.
C. D.
4.【新考法】(2023山东临沂罗庄二模)如图,一只松鼠先经过第一道门(A,B或C),再经过第二道门(D或E)出去,则松鼠走出笼子的路线是“先经过A门,再经过E门”的概率是( )
A. B. C. D.
5.【跨学科·物理】(2022山东烟台中考)如图所示的电路图中,同时闭合两个开关能形成闭合电路的概率是( )
A. B.
C. D.1
6.(2023山东临沂中考)在项目化学习中,“水是生命之源”项目组为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是( )
A. B. C. D.
7.【真实情境】(2023台湾省中考改编)盒玩的贩售方式是将一款玩具装在盒子中贩卖,购买者只能从外盒知道购买的是哪一系列玩具,但无法知道是系列中的哪一款,图1、图2分别为动物系列、汽车系列盒玩中所有可能出现的款式.
已知小友喜欢图1中的A款、C款,喜欢图2中的B款,若他打算购买图1的盒玩一盒,且他买到图1中每款玩具的机会相等;他也打算购买图2的盒玩一盒,且他买到图2中每款玩具的机会相等,则他买到的两盒盒玩内的玩具都是他喜欢的款式的概率为( )
A. B. C. D.
8.(2021山东烟台中考)连接正六边形不相邻的两个顶点,并将中间的六边形涂成灰色,制成如图所示的镖盘,将一枚飞镖任意投掷到镖盘上,飞镖落在阴影区域的概率为( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9.(2022山东青岛市南一模)林业部门要考察某种幼树在一定条件下的移植成活率,表格中是这种幼树在移植过程中的一组数据:
移植的棵数n 1 000 1 500 2 500 4 000
成活的棵数m 853 1 356 2 220 3 500
成活的频率 0.853 0.904 0.888 0.875
移植的棵数n 8 000 15 000 20 000 30 000
成活的棵数m 7 056 13 170 17 580 26 400
成活的频率 0.882 0.878 0.879 0.880
根据以上数据,该林业部门估计在此条件下移植的55 000棵该种幼树成活的棵数为 .
10.如图所示的是两个质地均匀的转盘,现转动转盘①和转盘②各一次,如果其中一个转盘转出了红色,另一个转盘转出了蓝色,就能配成紫色,则能配成紫色的概率为 .
转盘①
转盘②
11.小颖从某大型商场的东门进入后,开始自由购物,每走到一个十字道口,她自己可能直行,也可能向左转或向右转,且这三种可能性均相同,则经过两个十字道口后小颖向 方向参观的概率大.(填“东”“南”“西”“北”中的一个)
12.(2021内蒙古呼和浩特中考)动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此,若设刚出生的这种动物共有a只,则20年后存活的有 只,现年20岁的这种动物活到25岁的概率是 .
13.【新考法】(2023山东聊城中考)在一个不透明的袋子中,装有五个分别标有数
-,,0,2,π的小球,这些小球除标的数外其他完全相同.从袋子中随机摸出两个小球,两球上的数之积恰好是有理数的概率为 .
三、解答题(共48分)
14.[含评分细则]【真实情境】(2023山东烟台一模)(8分)如图所示的是一个迷宫示意图,小明和小亮分别从入口进入,沿着虚线所示的路线行走,两人根据自己的选择随机进入A,B,C三个房间中的某一个.
(1)小明进入A房间的概率是多少
(2)利用树状图或表格,求出两人在走迷宫结束后,B房间至少有1个人的概率.
15.[含评分细则]【新素材】(2023四川南充中考)(8分)为培养学生劳动习惯,提升学生劳动技能,某校在五月第二周开展了劳动教育实践周活动.七(1)班提供了四类活动:A.物品整理,B.环境美化,C.植物栽培,D.工具制作.要求每个学生选择其中一项活动参加,该班数学科代表对全班学生参与四类活动情况进行了统计,并绘制成统计图(如图).
(1)已知该班有15人参加A类活动,则参加C类活动的有多少人
(2)该班参加D类活动的学生中有2名女生和2名男生获得一等奖,其中一名女生叫王丽,若从获得一等奖的学生中随机抽取两人参加学校“工具制作”比赛,求刚好抽中王丽和1名男生的概率.
16.[含评分细则](10分)甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.
(1)若开始时球在甲手中,则经过三次传球后,球传回到甲手中的概率是多少
(2)若乙想使球经过三次传递后,落在自己手中的概率最大,则乙应让球开始时在谁手中 请说明理由.
17.[含评分细则]【新独家原创】(10分)某超市在元旦期间进行购物促销活动,购物满88元即有一次抽奖机会.抽奖规则如下:一个不透明的箱子里装有若干个红色小球和1个白色小球(除颜色不同外,其他均相同),从箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球.若两次摸出的球都是白球,则中一等奖;若两次摸出的球只有一个白球,则中二等奖;若两次摸出的球没有白球,则不中奖.
(1)聪明的小卓通过观察发现每次摸到白色小球的频率稳定在0.25左右,请你估计箱子里红色小球的个数;
(2)在(1)的条件下,若小卓的妈妈有一次抽奖机会,试求小卓的妈妈中奖的概率.
18.[含评分细则]【真实情境】(2021陕西西安灞桥模拟)(12分)小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至3层的任意一层出电梯.
(1)请你用“画树状图”或“列表”的方法求甲、乙二人在同一层出电梯的概率;
(2)小亮和小芳做游戏,规则如下:若甲、乙在同一层或相邻层出电梯,则小亮胜,否则小芳胜.该游戏是否公平 请说明理由.
3层
2层
1层
地下车库
答案全解全析
1.B A项,明天下雨的概率为80%,只是说明明天下雨的可能性大,与时间无关,故本选项说法错误;B项说法正确;C项,某彩票中奖概率是1%,买100张这种彩票中奖是随机事件,不一定会有1张中奖,故本选项说法错误;D项,小明前几次的数学测试成绩都在90分以上,这次数学测试成绩不一定在90分以上,故本选项说法错误.故选B.
2.D ∵只有第二个图形既是轴对称图形又是中心对称图形,
∴小乐抽到的书签图案既是轴对称图形又是中心对称图形的概率=.
故选D.
3.B 将甲、乙、丙三种品牌分别记作A、B、C,列表如下:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
由表知,共有9种等可能的结果,其中他们都选到同一品牌的有3种结果,
所以他们都选到同一品牌的概率为=,故选B.
4.D 本题以松鼠走出笼子的路线为情境考查用列表法或画树状图法求概率.
画树状图如下:
共有6种等可能的结果,其中松鼠走出笼子的路线是“先经过A门,再经过E门”的只有1种结果,
所以松鼠走出笼子的路线是“先经过A门,再经过E门”的概率为.故选D.
5.B 把S1、S2、S3分别记为A、B、C,画树状图如下:
共有6种等可能的结果,其中同时闭合两个开关能形成闭合电路的结果有4种,即AB、AC、BA、CA,
∴同时闭合两个开关能形成闭合电路的概率为=,故选B.
6.D 画树状图如下:
共有12种等可能的结果,其中恰好抽到一名男生和一名女生的结果数为8,
所以恰好抽到一名男生和一名女生的概率==.故选D.
7.A 列表如下:
动物
系列 汽车
系列 A B C D E F
A (A,A) (B,A) (C,A) (D,A) (E,A) (F,A)
B (A,B) (B,B) (C,B) (D,B) (E,B) (F,B)
C (A,C) (B,C) (C,C) (D,C) (E,C) (F,C)
D (A,D) (B,D) (C,D) (D,D) (E,D) (F,D)
E (A,E) (B,E) (C,E) (D,E) (E,E) (F,E)
由表知,共有30种等可能的结果,其中小友买到的两盒盒玩内的玩具都是他喜欢的款式的结果有2种,
所以他买到的两盒盒玩内的玩具都是他喜欢的款式的概率为=,故选A.
8.B 添加辅助线如图所示,令S△ABC=a,
由题意可知,阴影区域为正六边形,则S阴影=6a,S大正六边形=18a,∴飞镖落在阴影区域的概率为=.故选B.
9.答案48 400
解析由题表中数据,可知幼树在移植过程中,成活的频率稳定在0.88附近,
所以估计这种幼树移植成活的概率为0.88,
则该林业部门估计在此条件下移植的55 000棵该种幼树成活的棵数为
55 000×0.88=48 400.
10.答案
解析将转盘①中红色部分等分成3部分,
画树状图如下:
由树状图可知,共有16种等可能的结果,其中能配成紫色的结果有8种,
所以能配成紫色的概率为=.
11.答案西
解析画树状图如图所示.
经过两个十字道口后,共有9种等可能的结果,其中向西的结果有3种,向东、北、南的结果都分别有2种,因此向西的概率为=,其他三个方向的概率都为,所以经过两个十字道口后小颖向西方向参观的概率大.
12.答案0.8a;
解析若刚出生的这种动物共有a只,则20年后存活的有0.8a只.设共有这种动物x只,则活到20岁的只数为0.8x,活到25岁的只数为0.5x,故现年20岁的这种动物活到25岁的概率为=.
13.答案
解析本题综合考查概率计算与实数运算.
根据题意画树状图如下:
共有20种等可能的结果,其中两球上的数之积恰好是有理数的结果有8种,
∴两球上的数字之积恰好是有理数的概率为=.
14.解析(1)共有3个房间,小明进入A房间的概率为. 2分
(2)列表如下:
小亮 小明 A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,共有9种等可能的结果,其中B房间至少有1个人的结果共有5种,
所以B房间至少有1个人的概率为. 8分
15.解析(1)该班总人数为15÷30%=50,
∴参加C类活动的有50×(1-30%-28%-22%)=50×20%=10(人). 3分
(2)把2名女生分别记为甲、乙(其中甲为王丽),2名男生分别记为丙、丁,
画树状图如下:
共有12种等可能的结果,其中刚好抽中王丽和1名男生的结果有4种,
∴刚好抽中王丽和1名男生的概率为=. 8分
16.解析(1)画树状图,如图所示:
由树状图可知,共有8种等可能的结果,经过三次传球后,球传回到甲手中的结果有2种,所以所求概率为=. 4分
(2)乙应让球开始时在甲手中或丙手中.
理由:由(1)可知,从甲开始传球,经过三次传球后,球传到甲手中的概率为,球传到乙、丙手中的概率均为,所以经过三次传球后,球回到乙手中的概率的最大值为,所以乙应让球开始时在甲手中或丙手中. 10分
17.解析(1)设红色小球有x个,
根据题意,得=0.25,解得x=3.
经检验,x=3是分式方程的解,且符合题意.
∴估计箱子里红色小球的个数为3. 3分
(2)列表如下:
红1 红2 红3 白
红1 (红1,红1) (红1,红2) (红1,红3) (红1,白)
红2 (红2,红1) (红2,红2) (红2,红3) (红2,白)
红3 (红3,红1) (红3,红2) (红3,红3) (红3,白)
白 (白,红1) (白,红2) (白,红3) (白,白)
共有16种等可能的结果,其中两次摸出的球含有白球的结果为7种,
∴小卓的妈妈中奖的概率为. 10分
18.解析(1)根据题意画树状图如下:
共有9种等可能的情况,其中甲、乙二人在同一层出电梯的情况有3种,
∴甲、乙二人在同一层出电梯的概率是=. 5分
(2)该游戏不公平.理由:9种等可能的情况中,甲、乙两人在相邻层出电梯的情况有4种,
∴小亮获胜的概率为=.
∴小芳获胜的概率为1-=.
∵>,∴该游戏不公平. 12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
