2024鲁教版五四制数学九年级下学期课时练--期末素养综合测试(一)(含解析)
文档属性
| 名称 | 2024鲁教版五四制数学九年级下学期课时练--期末素养综合测试(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 738.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 19:41:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024鲁教版五四制数学九年级下学期
期末素养综合测试(一)
第五章至第六章
满分120分,限时100分钟
一、选择题(每小题3分,共36分)
1.(2022河南郑州期末)下列说法正确的是( )
A.概率很小的事情不可能发生
B.投掷一枚质地均匀的硬币1 000次,正面朝上的次数一定是500次
C.13名同学中,至少有两人的出生月份相同是必然事件
D.从1,2,3,4,5中任取一个数是偶数的可能性比较大
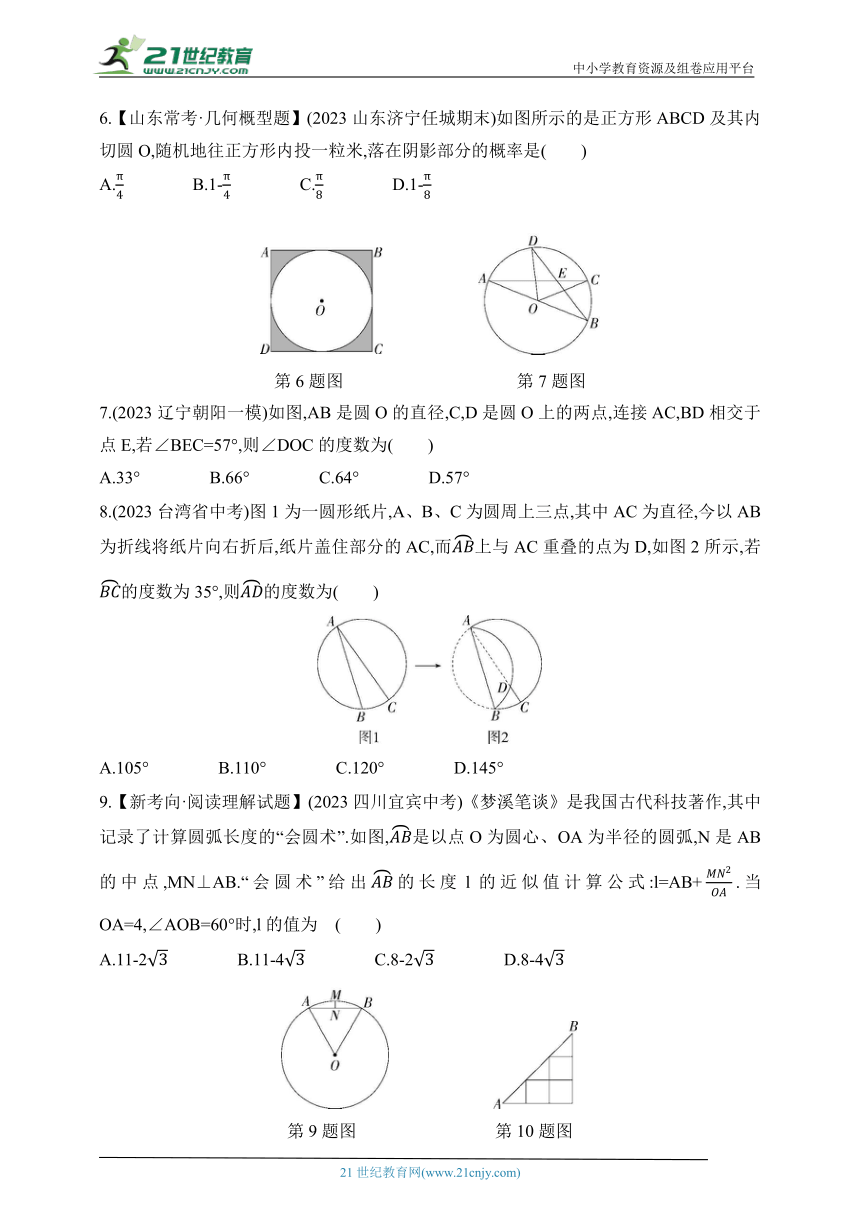
2.(2021山东临沂沂南期中)如图,☉O的半径OC=5,直线l⊥OC,垂足为H,且l交☉O于A、B两点,AB=8,若l沿OC所在直线平移后与☉O相切,则平移的距离是( )
A.1 B.2 C.8 D.2或8
3.(2023山东青岛莱西二模改编)如图,OA、OB、OC都是☉O的半径,若∠AOB是钝角,且∠AOB=2∠BOC,则下列结论正确的个数是( )
①AB=2BC;②=2;③∠ACB=2∠CAB;④∠ACB=∠BOC.
A.1 B.2 C.3 D.4
第3题图 第5题图
4.(2021山东东营中考)经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两辆汽车经过该路口,恰好有一辆汽车直行,另一辆汽车左拐的概率为(M9206001)( )
A. B. C. D.
5.(2023广东中考)如图,AB是☉O的直径,∠BAC=50°,则∠D=( )
A.20° B.40° C.50° D.80°
6.【山东常考·几何概型题】(2023山东济宁任城期末)如图所示的是正方形ABCD及其内切圆O,随机地往正方形内投一粒米,落在阴影部分的概率是( )
A. B.1- C. D.1-
第6题图 第7题图
7.(2023辽宁朝阳一模)如图,AB是圆O的直径,C,D是圆O上的两点,连接AC,BD相交于点E,若∠BEC=57°,则∠DOC的度数为( )
A.33° B.66° C.64° D.57°
8.(2023台湾省中考)图1为一圆形纸片,A、B、C为圆周上三点,其中AC为直径,今以AB为折线将纸片向右折后,纸片盖住部分的AC,而上与AC重叠的点为D,如图2所示,若的度数为35°,则的度数为( )
A.105° B.110° C.120° D.145°
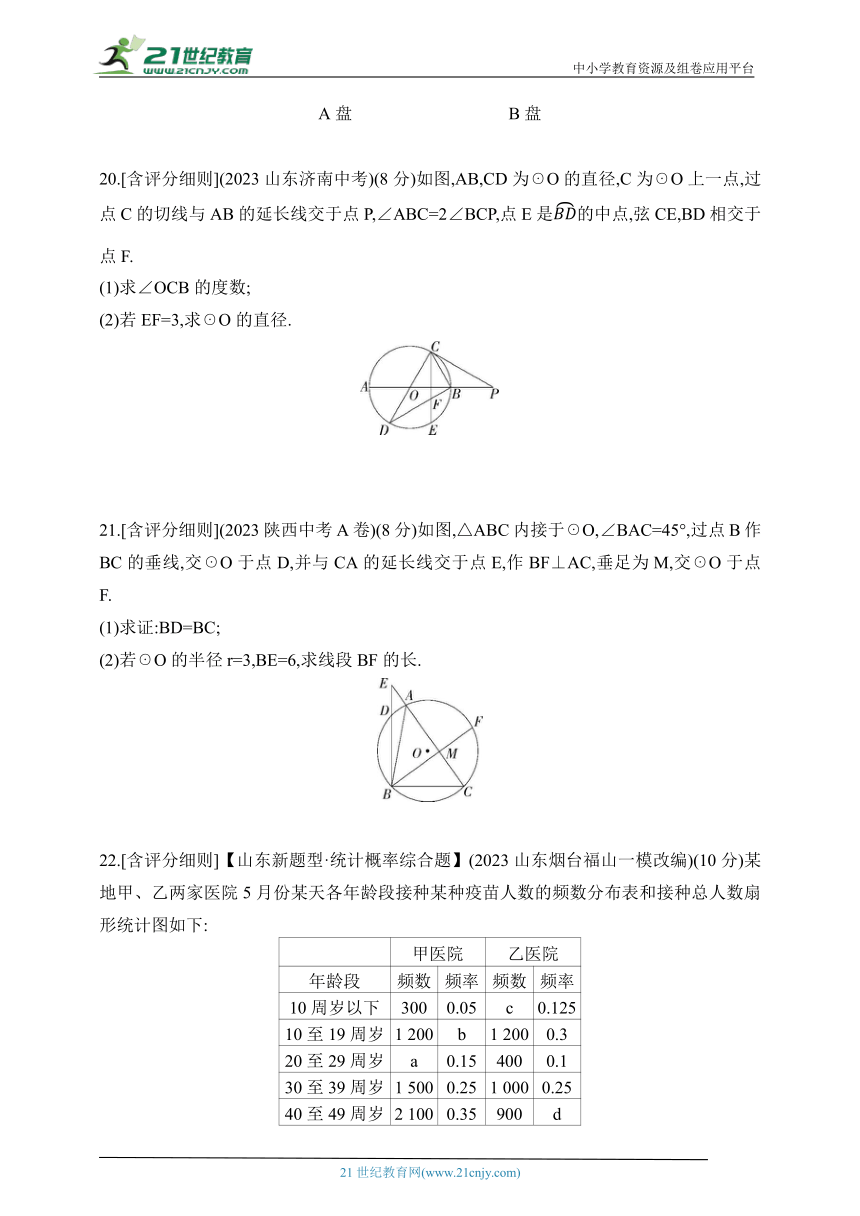
9.【新考向·阅读理解试题】(2023四川宜宾中考)《梦溪笔谈》是我国古代科技著作,其中记录了计算圆弧长度的“会圆术”.如图,是以点O为圆心、OA为半径的圆弧,N是AB的中点,MN⊥AB.“会圆术”给出的长度l的近似值计算公式:l=AB+.当OA=4,∠AOB=60°时,l的值为 ( )
A.11-2 B.11-4 C.8-2 D.8-4
第9题图 第10题图
10.如图所示的是一个沿3×3的正方形网格纸的对角线AB剪下的图形,一动点P由A点出发,沿格线每次向右或向上运动1个单位长度,则点P由A点运动到B点的不同路径共有( )
A.4条 B.5条 C.6条 D.7条
11.(2021山东烟台模拟)如图,已知所在圆的半径为5,所对的弦AB的长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,线段PB扫过的面积是( )
A.8π B.9π C.10π D.11π
12.(2023山东济宁任城期末)如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B,点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则给出结论正确的有( )
①PB=PD;②的长为π;③∠DBE=45°;④△BCF∽△PCB;⑤CF·CP为定值.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共18分)
13.【新独家原创】利用计算器进行模拟试验,12个人中有两个人同日过生日(以31天计,只考虑日期,不考虑月份)的频率稳定于0.914左右,据此估计12个人中有两个人同日过生日的概率为 .(精确到小数点后两位)
14.(2023湖南邵阳中考)如图,AD是☉O的直径,AB是☉O的弦,BC与☉O相切于点B,连接OB,若∠ABC=65°,则∠BOD的大小为 .
第14题图 第16题图
15.(2023黑龙江龙东地区中考)一个不透明的袋子中装有3个红球和2个白球,这些小球除颜色外完全相同,随机摸出两个小球,恰好是一红一白的概率是 .
16.(2023四川成都中考B卷)为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出.该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳 名观众同时观看演出.(π≈3.14,≈1.73)
17.(2022山东淄博博山二模)如图,在△ABC中,AB=AC=,∠B=30°,点O为BC上一点,以点O为圆心的圆与△ABC交于A,B,D三点,点E为直径BD下方半圆上一动点,连接AE,DE,AD,则图中阴影部分面积的最大值为 .
18.(2023四川广元中考)如图,∠ACB=45°,半径为2的☉O与角的两边相切,点P是☉O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设t=PE+PF,则t的取值范围是 .
三、解答题(本大题共7小题,共66分)
19.[含评分细则](2022山东青岛崂山一模)(8分)小明与小华用如图所示的A,B两个转盘进行配色游戏,A盘是四等分,B盘是三等分,其中一个转出红色一个转出蓝色即可配成紫色,分别转动两个转盘(指针指向分界线重新转动转盘),配成紫色时小明胜,否则小华胜,请用列表或画树状图的方法说明这个游戏是否公平.
A盘 B盘
20.[含评分细则](2023山东济南中考)(8分)如图,AB,CD为☉O的直径,C为☉O上一点,过点C的切线与AB的延长线交于点P,∠ABC=2∠BCP,点E是的中点,弦CE,BD相交于点F.
(1)求∠OCB的度数;
(2)若EF=3,求☉O的直径.
21.[含评分细则](2023陕西中考A卷)(8分)如图,△ABC内接于☉O,∠BAC=45°,过点B作BC的垂线,交☉O于点D,并与CA的延长线交于点E,作BF⊥AC,垂足为M,交☉O于点F.
(1)求证:BD=BC;
(2)若☉O的半径r=3,BE=6,求线段BF的长.
22.[含评分细则]【山东新题型·统计概率综合题】(2023山东烟台福山一模改编)(10分)某地甲、乙两家医院5月份某天各年龄段接种某种疫苗人数的频数分布表和接种总人数扇形统计图如下:
甲医院 乙医院
年龄段 频数 频率 频数 频率
10周岁以下 300 0.05 c 0.125
10至19周岁 1 200 b 1 200 0.3
20至29周岁 a 0.15 400 0.1
30至39周岁 1 500 0.25 1 000 0.25
40至49周岁 2 100 0.35 900 d
(1)根据上面图表信息,回答下列问题:
①填空:a= ,b= ,c= ,d= ;
②在甲、乙两医院当天接种疫苗的所有人员中,10至19周岁年龄段人数在扇形统计图中所占圆心角为 .
(2)若A、B、C三人都于当天随机到这两家医院接种疫苗,画树状图展示所有等可能的结果,并求这三人同时在乙医院接种的概率.
23.[含评分细则](2023黑龙江齐齐哈尔中考)(10分)如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E是斜边AC上一点,以AE为直径的☉O经过点D,交AB于点F,连接DF.
(1)求证:BC是☉O的切线;
(2)若BD=5,tan∠ADB=,求图中阴影部分的面积.(结果保留π)
24.[含评分细则]【操作探究问题】(2023河北中考)(10分)装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50 cm,如图1和图2所示,MN为水面截线,GH为台面截线,MN∥GH.
计算 在图1中,已知MN=48 cm,作OC⊥MN于点C.
(1)求OC的长.
操作 将图1中的水槽沿GH向右作无滑动的滚动,使水流出一部分,当∠ANM=30°时停止滚动,如图2.其中,半圆的中点为Q,GH与半圆的切点为E.连接OE交MN于点D.
探究 在图2中.
(2)操作后水面高度下降了多少
(3)连接OQ并延长交GH于点F,求线段EF与的长度,并比较大小.
图1
图2
25.[含评分细则](2023山东菏泽中考)(12分)如图,AB为☉O的直径,C是圆上一点,D是的中点,弦DE⊥AB,垂足为点F.
(1)求证:BC=DE;
(2)P是上一点,AC=6,BF=2,求tan∠BPC;
(3)在(2)的条件下,当CP是∠ACB的平分线时,求CP的长.
答案全解全解
1.C A项,概率很小的事情也可能发生,故本选项说法错误;
B项,投掷一枚质地均匀的硬币1 000次,正面朝上的次数不一定是500次,故本选项说法错误;
C项,13名同学中,至少有两人的出生月份相同是必然事件,故本选项说法正确;
D项,从1,2,3,4,5中任取一个数是奇数的可能性比较大,故本选项说法错误.故选C.
2.D 如图,连接OB.
∵AB⊥OC,∴AH=BH.∴BH=AB=×8=4.
∵OB=OC=5,∴在Rt△BOH中,OH==3.
∴当向下平移时,直线l平移的距离为5-3=2;
当向上平移时,直线l平移的距离为5+3=8.故选D.
3.C 如图,取的中点D,连接AD,BD.
①∵∠AOB=2∠BOC,∴=2.∴==.∴AD=BD=BC.
∵AB②由①知,=2,故②正确.
③∵∠AOB=2∠BOC,∠BOC=2∠CAB,∴∠AOB=4∠CAB.
∵∠AOB=2∠ACB,∴∠ACB=2∠CAB,故③正确.
④∵∠BOC=2∠CAB,∠ACB=2∠CAB,∴∠ACB=∠BOC,故④正确.故选C.
4.A 画树状图如下:
共有9种等可能的结果,其中恰好有一辆汽车直行,另一辆汽车左拐的结果有2种,∴恰好有一辆汽车直行,另一辆汽车左拐的概率为,故选A.
5.B ∵AB是☉O的直径,∴∠ACB=90°.∴∠BAC+∠ABC=90°.
∵∠BAC=50°,∴∠ABC=40°.∴∠D=∠ABC=40°,故选B.
6.B 设圆的半径为a,则圆的面积为πa2,正方形面积为4a2,
故随机地往正方形内投一粒米,落在阴影部分的概率为=1-.故选B.
7.B 如图,连接BC.
∵AB是圆O的直径,∴∠ACB=90°.
∵∠BEC=57°,∴∠CBD=90°-∠BEC=90°-57°=33°.∴∠DOC=2∠CBD=2×33°=66°,故选B.
8.B ∵∠BAD=的度数=的度数,∴=.∵的度数=35°,AC是圆的直径,
∴的度数=的度数-的度数=的度数-的度数-的度数=180°-35°-35°=110°.故选B.
9.B 连接ON,如图.
∵N是AB的中点,∴ON⊥AB.又MN⊥AB,∴M,N,O共线.
∵OA=OB=4,∠AOB=60°,∴△AOB是等边三角形.∴AB=OA=4,∠OAN=60°.
∴ON=OA·sin A=4·sin 60°=2.∴MN=OM-ON=4-2.
∴l=AB+=4+=11-4.故选B.
10.B 如图,将各格点分别记为1、2、3、4、5、6、7、8.
画树状图如下:
由树状图可知,共有5种结果,即点P由A点运动到B点的不同路径共有5条.故选B.
11.D 设所在圆的圆心为O,连接OP,OA,AP,AP',AB',OP与AB交于点M,如图所示.
∵所在圆的半径为5,弦AB的长为8,点P是的中点,
∴OP⊥AB,AM=BM=AB=4.∴OM==3.∴PM=5-3=2.
∴PA==2.
∴线段PB扫过的面积=S扇形BAB'-S扇形PAP'=-=16π-5π=11π.故选D.
12.C ①解法一(动态想象):∵点P为上一动点,
∴∠PBD与∠PDB的度数随点P的运动而变化,它们的变化趋势相反.
∴PB不一定等于PD,故①错误.
解法二(推理论证):连接AC并延长,与BD的延长线交于点H,如图.
∵M,C是半圆上的三等分点,
∴∠BOC=×180°=60°.∴∠BAH=∠BOC=30°.
∵BD与半圆O相切于点B,∴∠ABD=90°.∴∠PBD=90°-∠ABP,∠H=60°.
∵∠ACP=∠ABP,∠ACP=∠DCH,∴∠PDB=∠H+∠DCH=∠ABP+60°.
若∠PDB=∠PBD,则∠ABP+60°=90°-∠ABP,∴∠ABP=15°.
易知此时点P为的中点,这与P为上的一动点不完全吻合,
∴∠PDB不一定等于∠PBD.∴PB不一定等于PD,故①错误.
②由①知∠BOC=60°.∵AB=8,∴OB=OC=4.
∴的长度==π,故②正确.
③∵∠BOC=60°,OB=OC,∴△BOC是等边三角形.
∴∠ABC=60°.∵BE⊥OC,∴∠OBE=∠CBE=30°.
∵∠ABD=90°,∴∠DBE=60°,故③错误.
④∵∠BPC=∠BOC=30°,∠CBF=30°,∴∠CBF=∠BPC.
又∠BCF=∠PCB,∴△BCF∽△PCB,故④正确.
⑤∵△BCF∽△PCB,∴=.∴CF·CP=CB2.
∵CB=OB=4,∴CF·CP=16,故⑤正确.
综上所述,正确结论有②④⑤,共3个.故选C.
13.答案0.91
解析由频率估计概率知,12个人中有两个人同日过生日的概率约为0.91.
14.答案50°
解析∵BC与☉O相切于点B,∴OB⊥BC.∴∠OBC=90°.∵∠ABC=65°,
∴∠OBA=∠OBC-∠ABC=25°.∵OB=OA,∴∠OAB=∠OBA=25°.∴∠BOD=2∠OAB=50°.
15.答案
解析画树状图如下:
共有20种等可能的结果,其中恰好是一红一白的结果有12种,
∴恰好是一红一白的概率是=.
16.答案184
解析如图,过O作OD⊥AB,垂足为D.
则AD=BD,OD=5米.∵OA=OB,∴∠AOB=2∠AOD.
∵cos∠AOD===,∴∠AOD=60°.
∴AD=OA·sin∠AOD=5米,∠AOB=120°.∴AB=10米.
∴S阴影=S扇形AOB-S△OAB
=-×10×5=π-25≈61.4(平方米).
∵61.4×3≈184(名),∴最多可容纳184名观众同时观看演出.
17.答案+
解析如图,过O作OM⊥AD,垂足为M,延长MO交圆O于F,连接AF,DF,OA.
∵弓形AD的面积是定值,∴要使阴影部分的面积最大,则使△ADE的面积最大即可.
当E,F重合时,△ADE的面积最大,此时阴影部分的面积最大.
∵∠B=30°,∴∠AOD=60°.∵BD是圆O的直径,
∴∠BAD=90°.∴AD=AB·tan B=·tan 30°=1.∴BD=2.
∴阴影部分面积的最大值=S扇形AOD+S△OAF+S△ODF=+×1×(FM-OM) =+×1×1=+.
18.答案2≤t≤4+2
解析设半径为2的☉O与∠ACB的两边相切于M,N,连接OM,ON,延长NO交CB于D,∴∠CND=∠OMD=90°.
∵∠ACB=45°,∴△CND是等腰直角三角形.
∴∠CDN=45°.∵ON=OM=2,∴OD=2.
∴CN=DN=2+2,
延长EP交BC于Q,同理可得CE=EQ,PQ=PF,
∴t=PE+PF=PE+PQ=EQ.
如图1,当EQ与☉O相切且点P在圆心的右侧时,t有最大值.
图1
连接OP,则四边形ENOP是正方形.∴EN=OP=2.∴t=EQ=CE=CN+EN=2+2+2=4+2.
如图2,当EQ与☉O相切且点P在圆心的左侧时,t有最小值.
图2
同理可得t=2.
故t的取值范围是2≤t≤4+2.
19.解析列表如下:
红 红 红 蓝
红 (红,红) (红,红) (红,红) (蓝,红)
蓝 (红,蓝) (红,蓝) (红,蓝) (蓝,蓝)
蓝 (红,蓝) (红,蓝) (红,蓝) (蓝,蓝)
由表知,共有12种等可能的结果,其中可配成紫色的结果有7种, 5分
∴小明胜的概率为,∴小华胜的概率为1-=, 7分
∵≠,∴这个游戏不公平. 8分
20.解析(1)∵PC与☉O相切于点C,
∴OC⊥PC. 1分
∴∠OCB+∠BCP=90°.∵OB=OC,∴∠OCB=∠OBC. 2分
∵∠ABC=2∠BCP,∴∠OCB=2∠BCP.
∴3∠BCP=90°.∴∠BCP=30°.∴∠OCB=60°. 3分
(2)如图, 连接DE. 4分
∵CD是☉O的直径,∴∠DEC=90°. 5分
∵点E是的中点,∴=.
∴∠DCE=∠ECB=∠FDE=∠DCB=30°. 6分
在Rt△FDE中,EF=3,∠FDE=30°,
∴DE==3. 7分
在Rt△DEC中,∠DCE=30°,∴CD=2DE=6.
∴☉O的直径为6. 8分
21.解析(1)证明:如图,连接DC,则∠BDC=∠BAC=45°. 1分
∵BD⊥BC,∴∠DBC=90°.∴∠BCD=90°-∠BDC=45°.
∴∠BCD=∠BDC.∴BD=BC. 3分
(2)∵∠DBC=90°,∴CD为☉O的直径,∴CD=2r=6.
∴BC=CD·sin∠BDC=6·sin 45°=3. 4分
∴EC===3.
∵∠BMC=∠EBC=90°,∠BCM=∠ECB,∴△BCM∽△ECB.∴==.
∴BM===2,CM===. 6分
如图,连接CF,则∠F=∠BAC=45°,∴∠MCF=45°.
∴MF=MC=. 7分
∴BF=BM+MF=2+. 8分
22.解析(1)①在甲医院接种人数为300÷0.05=6 000,∴a=6 000×0.15=900,b=1 200÷6 000=0.2.
在乙医院接种人数为1 200÷0.3=4 000,∴c=4 000×0.125=500,d=900÷4 000=0.225,
故答案为900;0.2;500;0.225. 4分
②在甲、乙两医院当天接种疫苗的所有人员中,10至19周岁年龄段人数为1 200+1 200=2 400,
∴10至19周岁年龄段人数在扇形统计图中所占圆心角为360°×=86.4°.
故答案为86.4°. 6分
(2)画树状图如下:
共有8种等可能的结果,其中A、B、C三人同时在乙医院接种的结果只有1种,
∴这三人同时在乙医院接种的概率为. 10分
23.解析(1)证明:如图,连接OD.
∵OA=OD,∴∠OAD=∠ODA.∵AD平分∠BAC,∴∠OAD=∠BAD.
∴∠ODA=∠BAD.∴OD∥AB.∴∠ODC=∠B=90°.∴半径OD⊥BC于点D.
∴BC是☉O的切线. 4分
(2)如图,连接OF,DE.
∵∠B=90°,tan∠ADB=,∴∠ADB=60°.∴∠BAD=30°.
∵BD=5,∴AD=2BD=10.∵AE是☉O的直径,∴∠ADE=90°.
∵AD平分∠BAC,∴∠DAE=∠BAD=30°.
在Rt△ADE中,AD=10,
∵cos∠DAE==,∴AE=.∴OA=AE=.
∵∠BAC=∠DAE+∠BAD=60°,OA=OF,∴△AOF是等边三角形.
∴∠AOF=60°.∵OD∥AB,∴S△ADF=S△AOF.
∴S阴影=S扇形AOF==. 10分
24.解析(1)如图,连接OM.
∵O为圆心,OC⊥MN于点C,MN=48 cm,
∴MC=MN=24 cm.∵AB=50 cm,∴OM=AB=25 cm.
在Rt△OMC中,OC===7(cm). 3分
(2)∵GH与半圆的切点为E,∴OE⊥GH.∵MN∥GH,∴OE⊥MN.
∵∠ANM=30°,ON=25 cm,∴OD=ON= cm.
∴操作后水面高度下降-7=(cm). 6分
(3)∵OE⊥MN于点D,∠ANM=30°,∴∠DOB=60°.
∵半圆的中点为Q,∴=.∴∠QOB=90°.
∴∠QOE=30°,∴EF=OE·tan∠QOE=(cm),
的长为=(cm). 9分
∵-π==>0,
∴>.
∴EF的长度>的长度. 10分
25.解析(1)证明:∵D是的中点,∴=.
∵DE⊥AB且AB为☉O的直径,∴=.
∴=.∴BC=DE. 2分
(2)如图,连接OD.
∵=,∴∠CAB=的度数=∠DOB.
∵AB为☉O的直径,∴∠ACB=90°.
∵DE⊥AB,∴∠DFO=90°.∴∠ACB=∠DFO.∴△ACB∽△OFD.
∴=.
设☉O的半径为r,则OF=OB-BF=r-2.
∴=,解得r=5.
经检验,r=5是分式方程的根,且符合题意.
∴AB=2r=10.∴BC==8.
∴tan∠CAB===.
∵∠BPC=∠CAB,∴tan∠BPC=. 7分
(3)如图,过点B作BG⊥CP于点G.
∴∠BGC=∠BGP=90°.∵∠ACB=90°,CP平分∠ACB,
∴∠ACP=∠BCP=45°.∴∠CBG=45°.
∴CG=BG=BC·sin∠BCP=8·sin 45°=4.
∵tan∠BPC==,∴GP=3.
∴CP=CG+GP=4+3=7. 12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版五四制数学九年级下学期
期末素养综合测试(一)
第五章至第六章
满分120分,限时100分钟
一、选择题(每小题3分,共36分)
1.(2022河南郑州期末)下列说法正确的是( )
A.概率很小的事情不可能发生
B.投掷一枚质地均匀的硬币1 000次,正面朝上的次数一定是500次
C.13名同学中,至少有两人的出生月份相同是必然事件
D.从1,2,3,4,5中任取一个数是偶数的可能性比较大
2.(2021山东临沂沂南期中)如图,☉O的半径OC=5,直线l⊥OC,垂足为H,且l交☉O于A、B两点,AB=8,若l沿OC所在直线平移后与☉O相切,则平移的距离是( )
A.1 B.2 C.8 D.2或8
3.(2023山东青岛莱西二模改编)如图,OA、OB、OC都是☉O的半径,若∠AOB是钝角,且∠AOB=2∠BOC,则下列结论正确的个数是( )
①AB=2BC;②=2;③∠ACB=2∠CAB;④∠ACB=∠BOC.
A.1 B.2 C.3 D.4
第3题图 第5题图
4.(2021山东东营中考)经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两辆汽车经过该路口,恰好有一辆汽车直行,另一辆汽车左拐的概率为(M9206001)( )
A. B. C. D.
5.(2023广东中考)如图,AB是☉O的直径,∠BAC=50°,则∠D=( )
A.20° B.40° C.50° D.80°
6.【山东常考·几何概型题】(2023山东济宁任城期末)如图所示的是正方形ABCD及其内切圆O,随机地往正方形内投一粒米,落在阴影部分的概率是( )
A. B.1- C. D.1-
第6题图 第7题图
7.(2023辽宁朝阳一模)如图,AB是圆O的直径,C,D是圆O上的两点,连接AC,BD相交于点E,若∠BEC=57°,则∠DOC的度数为( )
A.33° B.66° C.64° D.57°
8.(2023台湾省中考)图1为一圆形纸片,A、B、C为圆周上三点,其中AC为直径,今以AB为折线将纸片向右折后,纸片盖住部分的AC,而上与AC重叠的点为D,如图2所示,若的度数为35°,则的度数为( )
A.105° B.110° C.120° D.145°
9.【新考向·阅读理解试题】(2023四川宜宾中考)《梦溪笔谈》是我国古代科技著作,其中记录了计算圆弧长度的“会圆术”.如图,是以点O为圆心、OA为半径的圆弧,N是AB的中点,MN⊥AB.“会圆术”给出的长度l的近似值计算公式:l=AB+.当OA=4,∠AOB=60°时,l的值为 ( )
A.11-2 B.11-4 C.8-2 D.8-4
第9题图 第10题图
10.如图所示的是一个沿3×3的正方形网格纸的对角线AB剪下的图形,一动点P由A点出发,沿格线每次向右或向上运动1个单位长度,则点P由A点运动到B点的不同路径共有( )
A.4条 B.5条 C.6条 D.7条
11.(2021山东烟台模拟)如图,已知所在圆的半径为5,所对的弦AB的长为8,点P是的中点,将绕点A逆时针旋转90°后得到,则在该旋转过程中,线段PB扫过的面积是( )
A.8π B.9π C.10π D.11π
12.(2023山东济宁任城期末)如图,AB为半圆O的直径,M,C是半圆上的三等分点,AB=8,BD与半圆O相切于点B,点P为上一动点(不与点A,M重合),直线PC交BD于点D,BE⊥OC于点E,延长BE交PC于点F,则给出结论正确的有( )
①PB=PD;②的长为π;③∠DBE=45°;④△BCF∽△PCB;⑤CF·CP为定值.
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分,共18分)
13.【新独家原创】利用计算器进行模拟试验,12个人中有两个人同日过生日(以31天计,只考虑日期,不考虑月份)的频率稳定于0.914左右,据此估计12个人中有两个人同日过生日的概率为 .(精确到小数点后两位)
14.(2023湖南邵阳中考)如图,AD是☉O的直径,AB是☉O的弦,BC与☉O相切于点B,连接OB,若∠ABC=65°,则∠BOD的大小为 .
第14题图 第16题图
15.(2023黑龙江龙东地区中考)一个不透明的袋子中装有3个红球和2个白球,这些小球除颜色外完全相同,随机摸出两个小球,恰好是一红一白的概率是 .
16.(2023四川成都中考B卷)为传承非遗文化,讲好中国故事,某地准备在一个场馆进行川剧演出.该场馆底面为一个圆形,如图所示,其半径是10米,从A到B有一笔直的栏杆,圆心O到栏杆AB的距离是5米,观众在阴影区域里观看演出,如果每平方米可以坐3名观众,那么最多可容纳 名观众同时观看演出.(π≈3.14,≈1.73)
17.(2022山东淄博博山二模)如图,在△ABC中,AB=AC=,∠B=30°,点O为BC上一点,以点O为圆心的圆与△ABC交于A,B,D三点,点E为直径BD下方半圆上一动点,连接AE,DE,AD,则图中阴影部分面积的最大值为 .
18.(2023四川广元中考)如图,∠ACB=45°,半径为2的☉O与角的两边相切,点P是☉O上任意一点,过点P向角的两边作垂线,垂足分别为E,F,设t=PE+PF,则t的取值范围是 .
三、解答题(本大题共7小题,共66分)
19.[含评分细则](2022山东青岛崂山一模)(8分)小明与小华用如图所示的A,B两个转盘进行配色游戏,A盘是四等分,B盘是三等分,其中一个转出红色一个转出蓝色即可配成紫色,分别转动两个转盘(指针指向分界线重新转动转盘),配成紫色时小明胜,否则小华胜,请用列表或画树状图的方法说明这个游戏是否公平.
A盘 B盘
20.[含评分细则](2023山东济南中考)(8分)如图,AB,CD为☉O的直径,C为☉O上一点,过点C的切线与AB的延长线交于点P,∠ABC=2∠BCP,点E是的中点,弦CE,BD相交于点F.
(1)求∠OCB的度数;
(2)若EF=3,求☉O的直径.
21.[含评分细则](2023陕西中考A卷)(8分)如图,△ABC内接于☉O,∠BAC=45°,过点B作BC的垂线,交☉O于点D,并与CA的延长线交于点E,作BF⊥AC,垂足为M,交☉O于点F.
(1)求证:BD=BC;
(2)若☉O的半径r=3,BE=6,求线段BF的长.
22.[含评分细则]【山东新题型·统计概率综合题】(2023山东烟台福山一模改编)(10分)某地甲、乙两家医院5月份某天各年龄段接种某种疫苗人数的频数分布表和接种总人数扇形统计图如下:
甲医院 乙医院
年龄段 频数 频率 频数 频率
10周岁以下 300 0.05 c 0.125
10至19周岁 1 200 b 1 200 0.3
20至29周岁 a 0.15 400 0.1
30至39周岁 1 500 0.25 1 000 0.25
40至49周岁 2 100 0.35 900 d
(1)根据上面图表信息,回答下列问题:
①填空:a= ,b= ,c= ,d= ;
②在甲、乙两医院当天接种疫苗的所有人员中,10至19周岁年龄段人数在扇形统计图中所占圆心角为 .
(2)若A、B、C三人都于当天随机到这两家医院接种疫苗,画树状图展示所有等可能的结果,并求这三人同时在乙医院接种的概率.
23.[含评分细则](2023黑龙江齐齐哈尔中考)(10分)如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E是斜边AC上一点,以AE为直径的☉O经过点D,交AB于点F,连接DF.
(1)求证:BC是☉O的切线;
(2)若BD=5,tan∠ADB=,求图中阴影部分的面积.(结果保留π)
24.[含评分细则]【操作探究问题】(2023河北中考)(10分)装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50 cm,如图1和图2所示,MN为水面截线,GH为台面截线,MN∥GH.
计算 在图1中,已知MN=48 cm,作OC⊥MN于点C.
(1)求OC的长.
操作 将图1中的水槽沿GH向右作无滑动的滚动,使水流出一部分,当∠ANM=30°时停止滚动,如图2.其中,半圆的中点为Q,GH与半圆的切点为E.连接OE交MN于点D.
探究 在图2中.
(2)操作后水面高度下降了多少
(3)连接OQ并延长交GH于点F,求线段EF与的长度,并比较大小.
图1
图2
25.[含评分细则](2023山东菏泽中考)(12分)如图,AB为☉O的直径,C是圆上一点,D是的中点,弦DE⊥AB,垂足为点F.
(1)求证:BC=DE;
(2)P是上一点,AC=6,BF=2,求tan∠BPC;
(3)在(2)的条件下,当CP是∠ACB的平分线时,求CP的长.
答案全解全解
1.C A项,概率很小的事情也可能发生,故本选项说法错误;
B项,投掷一枚质地均匀的硬币1 000次,正面朝上的次数不一定是500次,故本选项说法错误;
C项,13名同学中,至少有两人的出生月份相同是必然事件,故本选项说法正确;
D项,从1,2,3,4,5中任取一个数是奇数的可能性比较大,故本选项说法错误.故选C.
2.D 如图,连接OB.
∵AB⊥OC,∴AH=BH.∴BH=AB=×8=4.
∵OB=OC=5,∴在Rt△BOH中,OH==3.
∴当向下平移时,直线l平移的距离为5-3=2;
当向上平移时,直线l平移的距离为5+3=8.故选D.
3.C 如图,取的中点D,连接AD,BD.
①∵∠AOB=2∠BOC,∴=2.∴==.∴AD=BD=BC.
∵AB
③∵∠AOB=2∠BOC,∠BOC=2∠CAB,∴∠AOB=4∠CAB.
∵∠AOB=2∠ACB,∴∠ACB=2∠CAB,故③正确.
④∵∠BOC=2∠CAB,∠ACB=2∠CAB,∴∠ACB=∠BOC,故④正确.故选C.
4.A 画树状图如下:
共有9种等可能的结果,其中恰好有一辆汽车直行,另一辆汽车左拐的结果有2种,∴恰好有一辆汽车直行,另一辆汽车左拐的概率为,故选A.
5.B ∵AB是☉O的直径,∴∠ACB=90°.∴∠BAC+∠ABC=90°.
∵∠BAC=50°,∴∠ABC=40°.∴∠D=∠ABC=40°,故选B.
6.B 设圆的半径为a,则圆的面积为πa2,正方形面积为4a2,
故随机地往正方形内投一粒米,落在阴影部分的概率为=1-.故选B.
7.B 如图,连接BC.
∵AB是圆O的直径,∴∠ACB=90°.
∵∠BEC=57°,∴∠CBD=90°-∠BEC=90°-57°=33°.∴∠DOC=2∠CBD=2×33°=66°,故选B.
8.B ∵∠BAD=的度数=的度数,∴=.∵的度数=35°,AC是圆的直径,
∴的度数=的度数-的度数=的度数-的度数-的度数=180°-35°-35°=110°.故选B.
9.B 连接ON,如图.
∵N是AB的中点,∴ON⊥AB.又MN⊥AB,∴M,N,O共线.
∵OA=OB=4,∠AOB=60°,∴△AOB是等边三角形.∴AB=OA=4,∠OAN=60°.
∴ON=OA·sin A=4·sin 60°=2.∴MN=OM-ON=4-2.
∴l=AB+=4+=11-4.故选B.
10.B 如图,将各格点分别记为1、2、3、4、5、6、7、8.
画树状图如下:
由树状图可知,共有5种结果,即点P由A点运动到B点的不同路径共有5条.故选B.
11.D 设所在圆的圆心为O,连接OP,OA,AP,AP',AB',OP与AB交于点M,如图所示.
∵所在圆的半径为5,弦AB的长为8,点P是的中点,
∴OP⊥AB,AM=BM=AB=4.∴OM==3.∴PM=5-3=2.
∴PA==2.
∴线段PB扫过的面积=S扇形BAB'-S扇形PAP'=-=16π-5π=11π.故选D.
12.C ①解法一(动态想象):∵点P为上一动点,
∴∠PBD与∠PDB的度数随点P的运动而变化,它们的变化趋势相反.
∴PB不一定等于PD,故①错误.
解法二(推理论证):连接AC并延长,与BD的延长线交于点H,如图.
∵M,C是半圆上的三等分点,
∴∠BOC=×180°=60°.∴∠BAH=∠BOC=30°.
∵BD与半圆O相切于点B,∴∠ABD=90°.∴∠PBD=90°-∠ABP,∠H=60°.
∵∠ACP=∠ABP,∠ACP=∠DCH,∴∠PDB=∠H+∠DCH=∠ABP+60°.
若∠PDB=∠PBD,则∠ABP+60°=90°-∠ABP,∴∠ABP=15°.
易知此时点P为的中点,这与P为上的一动点不完全吻合,
∴∠PDB不一定等于∠PBD.∴PB不一定等于PD,故①错误.
②由①知∠BOC=60°.∵AB=8,∴OB=OC=4.
∴的长度==π,故②正确.
③∵∠BOC=60°,OB=OC,∴△BOC是等边三角形.
∴∠ABC=60°.∵BE⊥OC,∴∠OBE=∠CBE=30°.
∵∠ABD=90°,∴∠DBE=60°,故③错误.
④∵∠BPC=∠BOC=30°,∠CBF=30°,∴∠CBF=∠BPC.
又∠BCF=∠PCB,∴△BCF∽△PCB,故④正确.
⑤∵△BCF∽△PCB,∴=.∴CF·CP=CB2.
∵CB=OB=4,∴CF·CP=16,故⑤正确.
综上所述,正确结论有②④⑤,共3个.故选C.
13.答案0.91
解析由频率估计概率知,12个人中有两个人同日过生日的概率约为0.91.
14.答案50°
解析∵BC与☉O相切于点B,∴OB⊥BC.∴∠OBC=90°.∵∠ABC=65°,
∴∠OBA=∠OBC-∠ABC=25°.∵OB=OA,∴∠OAB=∠OBA=25°.∴∠BOD=2∠OAB=50°.
15.答案
解析画树状图如下:
共有20种等可能的结果,其中恰好是一红一白的结果有12种,
∴恰好是一红一白的概率是=.
16.答案184
解析如图,过O作OD⊥AB,垂足为D.
则AD=BD,OD=5米.∵OA=OB,∴∠AOB=2∠AOD.
∵cos∠AOD===,∴∠AOD=60°.
∴AD=OA·sin∠AOD=5米,∠AOB=120°.∴AB=10米.
∴S阴影=S扇形AOB-S△OAB
=-×10×5=π-25≈61.4(平方米).
∵61.4×3≈184(名),∴最多可容纳184名观众同时观看演出.
17.答案+
解析如图,过O作OM⊥AD,垂足为M,延长MO交圆O于F,连接AF,DF,OA.
∵弓形AD的面积是定值,∴要使阴影部分的面积最大,则使△ADE的面积最大即可.
当E,F重合时,△ADE的面积最大,此时阴影部分的面积最大.
∵∠B=30°,∴∠AOD=60°.∵BD是圆O的直径,
∴∠BAD=90°.∴AD=AB·tan B=·tan 30°=1.∴BD=2.
∴阴影部分面积的最大值=S扇形AOD+S△OAF+S△ODF=+×1×(FM-OM) =+×1×1=+.
18.答案2≤t≤4+2
解析设半径为2的☉O与∠ACB的两边相切于M,N,连接OM,ON,延长NO交CB于D,∴∠CND=∠OMD=90°.
∵∠ACB=45°,∴△CND是等腰直角三角形.
∴∠CDN=45°.∵ON=OM=2,∴OD=2.
∴CN=DN=2+2,
延长EP交BC于Q,同理可得CE=EQ,PQ=PF,
∴t=PE+PF=PE+PQ=EQ.
如图1,当EQ与☉O相切且点P在圆心的右侧时,t有最大值.
图1
连接OP,则四边形ENOP是正方形.∴EN=OP=2.∴t=EQ=CE=CN+EN=2+2+2=4+2.
如图2,当EQ与☉O相切且点P在圆心的左侧时,t有最小值.
图2
同理可得t=2.
故t的取值范围是2≤t≤4+2.
19.解析列表如下:
红 红 红 蓝
红 (红,红) (红,红) (红,红) (蓝,红)
蓝 (红,蓝) (红,蓝) (红,蓝) (蓝,蓝)
蓝 (红,蓝) (红,蓝) (红,蓝) (蓝,蓝)
由表知,共有12种等可能的结果,其中可配成紫色的结果有7种, 5分
∴小明胜的概率为,∴小华胜的概率为1-=, 7分
∵≠,∴这个游戏不公平. 8分
20.解析(1)∵PC与☉O相切于点C,
∴OC⊥PC. 1分
∴∠OCB+∠BCP=90°.∵OB=OC,∴∠OCB=∠OBC. 2分
∵∠ABC=2∠BCP,∴∠OCB=2∠BCP.
∴3∠BCP=90°.∴∠BCP=30°.∴∠OCB=60°. 3分
(2)如图, 连接DE. 4分
∵CD是☉O的直径,∴∠DEC=90°. 5分
∵点E是的中点,∴=.
∴∠DCE=∠ECB=∠FDE=∠DCB=30°. 6分
在Rt△FDE中,EF=3,∠FDE=30°,
∴DE==3. 7分
在Rt△DEC中,∠DCE=30°,∴CD=2DE=6.
∴☉O的直径为6. 8分
21.解析(1)证明:如图,连接DC,则∠BDC=∠BAC=45°. 1分
∵BD⊥BC,∴∠DBC=90°.∴∠BCD=90°-∠BDC=45°.
∴∠BCD=∠BDC.∴BD=BC. 3分
(2)∵∠DBC=90°,∴CD为☉O的直径,∴CD=2r=6.
∴BC=CD·sin∠BDC=6·sin 45°=3. 4分
∴EC===3.
∵∠BMC=∠EBC=90°,∠BCM=∠ECB,∴△BCM∽△ECB.∴==.
∴BM===2,CM===. 6分
如图,连接CF,则∠F=∠BAC=45°,∴∠MCF=45°.
∴MF=MC=. 7分
∴BF=BM+MF=2+. 8分
22.解析(1)①在甲医院接种人数为300÷0.05=6 000,∴a=6 000×0.15=900,b=1 200÷6 000=0.2.
在乙医院接种人数为1 200÷0.3=4 000,∴c=4 000×0.125=500,d=900÷4 000=0.225,
故答案为900;0.2;500;0.225. 4分
②在甲、乙两医院当天接种疫苗的所有人员中,10至19周岁年龄段人数为1 200+1 200=2 400,
∴10至19周岁年龄段人数在扇形统计图中所占圆心角为360°×=86.4°.
故答案为86.4°. 6分
(2)画树状图如下:
共有8种等可能的结果,其中A、B、C三人同时在乙医院接种的结果只有1种,
∴这三人同时在乙医院接种的概率为. 10分
23.解析(1)证明:如图,连接OD.
∵OA=OD,∴∠OAD=∠ODA.∵AD平分∠BAC,∴∠OAD=∠BAD.
∴∠ODA=∠BAD.∴OD∥AB.∴∠ODC=∠B=90°.∴半径OD⊥BC于点D.
∴BC是☉O的切线. 4分
(2)如图,连接OF,DE.
∵∠B=90°,tan∠ADB=,∴∠ADB=60°.∴∠BAD=30°.
∵BD=5,∴AD=2BD=10.∵AE是☉O的直径,∴∠ADE=90°.
∵AD平分∠BAC,∴∠DAE=∠BAD=30°.
在Rt△ADE中,AD=10,
∵cos∠DAE==,∴AE=.∴OA=AE=.
∵∠BAC=∠DAE+∠BAD=60°,OA=OF,∴△AOF是等边三角形.
∴∠AOF=60°.∵OD∥AB,∴S△ADF=S△AOF.
∴S阴影=S扇形AOF==. 10分
24.解析(1)如图,连接OM.
∵O为圆心,OC⊥MN于点C,MN=48 cm,
∴MC=MN=24 cm.∵AB=50 cm,∴OM=AB=25 cm.
在Rt△OMC中,OC===7(cm). 3分
(2)∵GH与半圆的切点为E,∴OE⊥GH.∵MN∥GH,∴OE⊥MN.
∵∠ANM=30°,ON=25 cm,∴OD=ON= cm.
∴操作后水面高度下降-7=(cm). 6分
(3)∵OE⊥MN于点D,∠ANM=30°,∴∠DOB=60°.
∵半圆的中点为Q,∴=.∴∠QOB=90°.
∴∠QOE=30°,∴EF=OE·tan∠QOE=(cm),
的长为=(cm). 9分
∵-π==>0,
∴>.
∴EF的长度>的长度. 10分
25.解析(1)证明:∵D是的中点,∴=.
∵DE⊥AB且AB为☉O的直径,∴=.
∴=.∴BC=DE. 2分
(2)如图,连接OD.
∵=,∴∠CAB=的度数=∠DOB.
∵AB为☉O的直径,∴∠ACB=90°.
∵DE⊥AB,∴∠DFO=90°.∴∠ACB=∠DFO.∴△ACB∽△OFD.
∴=.
设☉O的半径为r,则OF=OB-BF=r-2.
∴=,解得r=5.
经检验,r=5是分式方程的根,且符合题意.
∴AB=2r=10.∴BC==8.
∴tan∠CAB===.
∵∠BPC=∠CAB,∴tan∠BPC=. 7分
(3)如图,过点B作BG⊥CP于点G.
∴∠BGC=∠BGP=90°.∵∠ACB=90°,CP平分∠ACB,
∴∠ACP=∠BCP=45°.∴∠CBG=45°.
∴CG=BG=BC·sin∠BCP=8·sin 45°=4.
∵tan∠BPC==,∴GP=3.
∴CP=CG+GP=4+3=7. 12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
