2024青岛版数学九年级下学期课时练--专项素养综合全练(八)求立体图形上两点间的最短路径问题(含解析)
文档属性
| 名称 | 2024青岛版数学九年级下学期课时练--专项素养综合全练(八)求立体图形上两点间的最短路径问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 439.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:30:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
专项素养综合全练(八)
求立体图形上两点间的最短路径问题
类型一 正方体问题
1.(2022陕西中考)如图所示的是一个棱长为1的正方体纸盒.若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是 ( )
A. B.2 C. D.3
2.(2022山东德州期中)如图,点A是正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是 .
3.如图1所示的正方体木块的棱长为6 cm,沿其相邻三个面的对角线(图1中虚线)切掉一角,得到如图2所示的几何体,一只蚂蚁沿着图2的几何体表面从顶点A爬行到顶点B的最短路程为 cm.
类型二 长方体问题
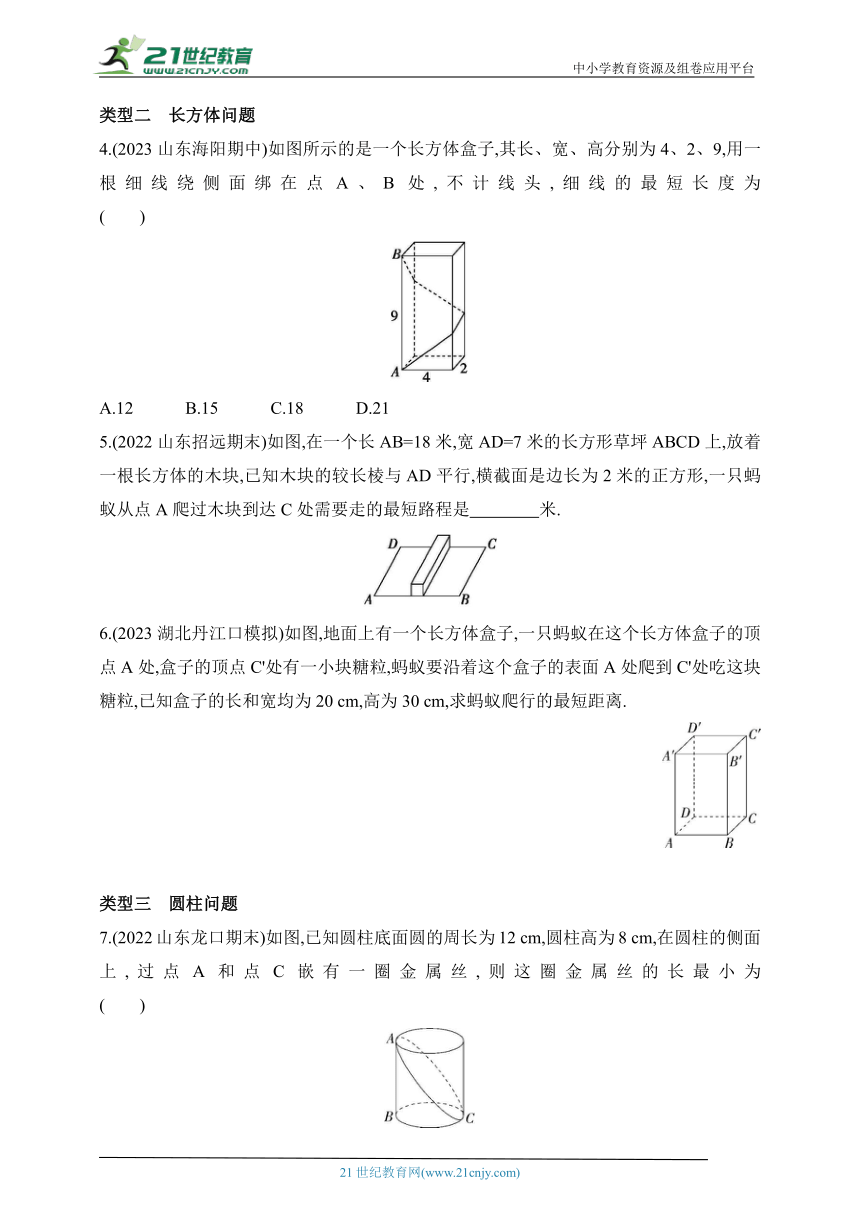
4.(2023山东海阳期中)如图所示的是一个长方体盒子,其长、宽、高分别为4、2、9,用一根细线绕侧面绑在点A、B处,不计线头,细线的最短长度为 ( )
A.12 B.15 C.18 D.21
5.(2022山东招远期末)如图,在一个长AB=18米,宽AD=7米的长方形草坪ABCD上,放着一根长方体的木块,已知木块的较长棱与AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A爬过木块到达C处需要走的最短路程是 米.
6.(2023湖北丹江口模拟)如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点C'处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到C'处吃这块糖粒,已知盒子的长和宽均为20 cm,高为30 cm,求蚂蚁爬行的最短距离.
类型三 圆柱问题
7.(2022山东龙口期末)如图,已知圆柱底面圆的周长为12 cm,圆柱高为8 cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长最小为 ( )
A.10 cm B.20 cm
C.4 cm D.100 cm
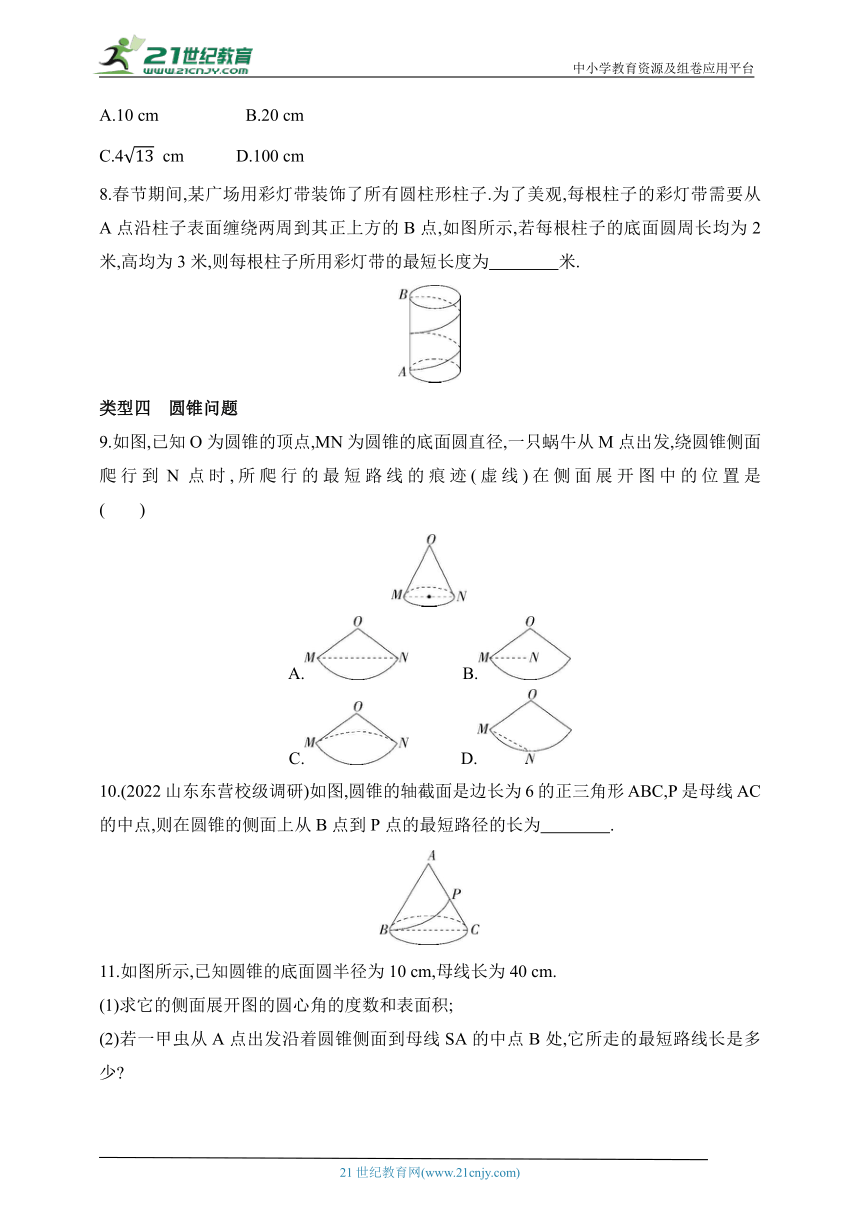
8.春节期间,某广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面圆周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为 米.
类型四 圆锥问题
9.如图,已知O为圆锥的顶点,MN为圆锥的底面圆直径,一只蜗牛从M点出发,绕圆锥侧面爬行到N点时,所爬行的最短路线的痕迹(虚线)在侧面展开图中的位置是 ( )
A. B.
C. D.
10.(2022山东东营校级调研)如图,圆锥的轴截面是边长为6的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路径的长为 .
11.如图所示,已知圆锥的底面圆半径为10 cm,母线长为40 cm.
(1)求它的侧面展开图的圆心角的度数和表面积;
(2)若一甲虫从A点出发沿着圆锥侧面到母线SA的中点B处,它所走的最短路线长是多少
答案全解全析
1.C 如图,将正方体的两个面展开,需要爬行的最短路程即为线段AB的长,
∵正方体的棱长为1,
∴BC=1,AC=2,
∴AB===,
∴需要爬行的最短路程为,故选C.
2.答案
解析 正方体的部分展开图如图.
过A作AE⊥CD于E,连接AB,则AB的长为蚂蚁爬行的最短路程,由题易知EC=1,BC=2,AE=1,∴BE=3,在Rt△ABE中,由勾股定理得AB==.
3.答案 (3+3)
解析 如图所示.连接AB交CD于E.
由题意知,△BCD是等腰直角三角形,△ACD是等边三角形,AB⊥CD,
在Rt△BCD中,CD==6 cm,
∴BE=CE=CD=3 cm,AC=6 cm,
在Rt△ACE中,AE==3 cm,
∴AB=BE+AE=(3+3)cm.
故蚂蚁从顶点A爬行到顶点B的最短路程为(3+3)cm.
4.B 将长方体的侧面沿AB展开,如图所示,连接AB',则AB'的长即为所用的细线的最短长度,
∵AA'=4+2+4+2=12,A'B'=AB=9,
∴AB'===15,故选B.
5.答案
解析 如图所示,连接AC,AC的长为蚂蚁需要走的最短路程.
由题意知AB=18+2×2=22米,BC=7米,在Rt△ABC中,AC===米.
6.解析 分两种情况:
①如图1,连接AC',
在Rt△ACC'中,AC=20+20=40(cm),CC'=30 cm,
根据勾股定理得,AC'===50(cm);
②如图2,连接AC',
在Rt△ABC'中,BC'=BB'+B'C'=30+20=50(cm),AB=20 cm,根据勾股定理得,AC'===10(cm).
∵10>50,
∴蚂蚁爬行的最短距离为50 cm.
7.B 如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的长最小为2AC的长度.
∵圆柱底面圆的周长为12 cm,高为8 cm,∴AB=8 cm,BC=BC'=6 cm,
在Rt△ABC中,AC===10 cm,
∴这圈金属丝的长最小为2AC=20 cm,故选B.
8.答案 5
解析 如图,连接AB,AB的长即为彩灯带的最短长度,
∵圆柱的高为3米,底面圆周长为2米,
∴AB==5(米),
∴每根柱子所用彩灯带的最短长度为5米.
9.D 因为MN为圆锥的底面圆直径,所以点N为侧面展开图中扇形弧的中点,只有D选项符合题意,故选D.
10.答案 3
解析 圆锥底面是以BC为直径的圆,圆的周长是6π,则以AB为一边,将圆锥的侧面展开,就得到一个以A为圆心,以AB的长为半径的扇形,弧长是6π.设展开后扇形的圆心角是n°,则=6π,解得n=180,∴展开后的扇形中∠BAC=×180°=90°,AP=AC=3,AB=6,∴在圆锥的侧面上从B点到P点的最短路径的长就是展开后扇形中线段BP的长,为=3.故答案为3.
11.解析 (1)设侧面展开图的圆心角为n°,
则=2π×10,∴n=90.
故侧面展开图的圆心角的度数为90°.
由题意知圆锥的表面积=π×102+π×10×40=500π(cm2).
(2)画出圆锥的侧面展开图如图,
由图可知,甲虫从A点出发沿着圆锥侧面到母线SA的中点B处,所走的最短路线是线段AB.
在Rt△ASB中,SA=40 cm,SB=20 cm,
∴AB==20(cm).
∴甲虫走的最短路线长是20 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
专项素养综合全练(八)
求立体图形上两点间的最短路径问题
类型一 正方体问题
1.(2022陕西中考)如图所示的是一个棱长为1的正方体纸盒.若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是 ( )
A. B.2 C. D.3
2.(2022山东德州期中)如图,点A是正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B的最短路程是 .
3.如图1所示的正方体木块的棱长为6 cm,沿其相邻三个面的对角线(图1中虚线)切掉一角,得到如图2所示的几何体,一只蚂蚁沿着图2的几何体表面从顶点A爬行到顶点B的最短路程为 cm.
类型二 长方体问题
4.(2023山东海阳期中)如图所示的是一个长方体盒子,其长、宽、高分别为4、2、9,用一根细线绕侧面绑在点A、B处,不计线头,细线的最短长度为 ( )
A.12 B.15 C.18 D.21
5.(2022山东招远期末)如图,在一个长AB=18米,宽AD=7米的长方形草坪ABCD上,放着一根长方体的木块,已知木块的较长棱与AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A爬过木块到达C处需要走的最短路程是 米.
6.(2023湖北丹江口模拟)如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点C'处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到C'处吃这块糖粒,已知盒子的长和宽均为20 cm,高为30 cm,求蚂蚁爬行的最短距离.
类型三 圆柱问题
7.(2022山东龙口期末)如图,已知圆柱底面圆的周长为12 cm,圆柱高为8 cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长最小为 ( )
A.10 cm B.20 cm
C.4 cm D.100 cm
8.春节期间,某广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面圆周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为 米.
类型四 圆锥问题
9.如图,已知O为圆锥的顶点,MN为圆锥的底面圆直径,一只蜗牛从M点出发,绕圆锥侧面爬行到N点时,所爬行的最短路线的痕迹(虚线)在侧面展开图中的位置是 ( )
A. B.
C. D.
10.(2022山东东营校级调研)如图,圆锥的轴截面是边长为6的正三角形ABC,P是母线AC的中点,则在圆锥的侧面上从B点到P点的最短路径的长为 .
11.如图所示,已知圆锥的底面圆半径为10 cm,母线长为40 cm.
(1)求它的侧面展开图的圆心角的度数和表面积;
(2)若一甲虫从A点出发沿着圆锥侧面到母线SA的中点B处,它所走的最短路线长是多少
答案全解全析
1.C 如图,将正方体的两个面展开,需要爬行的最短路程即为线段AB的长,
∵正方体的棱长为1,
∴BC=1,AC=2,
∴AB===,
∴需要爬行的最短路程为,故选C.
2.答案
解析 正方体的部分展开图如图.
过A作AE⊥CD于E,连接AB,则AB的长为蚂蚁爬行的最短路程,由题易知EC=1,BC=2,AE=1,∴BE=3,在Rt△ABE中,由勾股定理得AB==.
3.答案 (3+3)
解析 如图所示.连接AB交CD于E.
由题意知,△BCD是等腰直角三角形,△ACD是等边三角形,AB⊥CD,
在Rt△BCD中,CD==6 cm,
∴BE=CE=CD=3 cm,AC=6 cm,
在Rt△ACE中,AE==3 cm,
∴AB=BE+AE=(3+3)cm.
故蚂蚁从顶点A爬行到顶点B的最短路程为(3+3)cm.
4.B 将长方体的侧面沿AB展开,如图所示,连接AB',则AB'的长即为所用的细线的最短长度,
∵AA'=4+2+4+2=12,A'B'=AB=9,
∴AB'===15,故选B.
5.答案
解析 如图所示,连接AC,AC的长为蚂蚁需要走的最短路程.
由题意知AB=18+2×2=22米,BC=7米,在Rt△ABC中,AC===米.
6.解析 分两种情况:
①如图1,连接AC',
在Rt△ACC'中,AC=20+20=40(cm),CC'=30 cm,
根据勾股定理得,AC'===50(cm);
②如图2,连接AC',
在Rt△ABC'中,BC'=BB'+B'C'=30+20=50(cm),AB=20 cm,根据勾股定理得,AC'===10(cm).
∵10>50,
∴蚂蚁爬行的最短距离为50 cm.
7.B 如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的长最小为2AC的长度.
∵圆柱底面圆的周长为12 cm,高为8 cm,∴AB=8 cm,BC=BC'=6 cm,
在Rt△ABC中,AC===10 cm,
∴这圈金属丝的长最小为2AC=20 cm,故选B.
8.答案 5
解析 如图,连接AB,AB的长即为彩灯带的最短长度,
∵圆柱的高为3米,底面圆周长为2米,
∴AB==5(米),
∴每根柱子所用彩灯带的最短长度为5米.
9.D 因为MN为圆锥的底面圆直径,所以点N为侧面展开图中扇形弧的中点,只有D选项符合题意,故选D.
10.答案 3
解析 圆锥底面是以BC为直径的圆,圆的周长是6π,则以AB为一边,将圆锥的侧面展开,就得到一个以A为圆心,以AB的长为半径的扇形,弧长是6π.设展开后扇形的圆心角是n°,则=6π,解得n=180,∴展开后的扇形中∠BAC=×180°=90°,AP=AC=3,AB=6,∴在圆锥的侧面上从B点到P点的最短路径的长就是展开后扇形中线段BP的长,为=3.故答案为3.
11.解析 (1)设侧面展开图的圆心角为n°,
则=2π×10,∴n=90.
故侧面展开图的圆心角的度数为90°.
由题意知圆锥的表面积=π×102+π×10×40=500π(cm2).
(2)画出圆锥的侧面展开图如图,
由图可知,甲虫从A点出发沿着圆锥侧面到母线SA的中点B处,所走的最短路线是线段AB.
在Rt△ASB中,SA=40 cm,SB=20 cm,
∴AB==20(cm).
∴甲虫走的最短路线长是20 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
