2024青岛版数学九年级下学期课时练--专项素养综合全练(一)反比例函数中的面积问题(含解析)
文档属性
| 名称 | 2024青岛版数学九年级下学期课时练--专项素养综合全练(一)反比例函数中的面积问题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 425.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:35:49 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
专项素养综合全练(一)
反比例函数中的面积问题
类型一 一点一垂线
专题解读
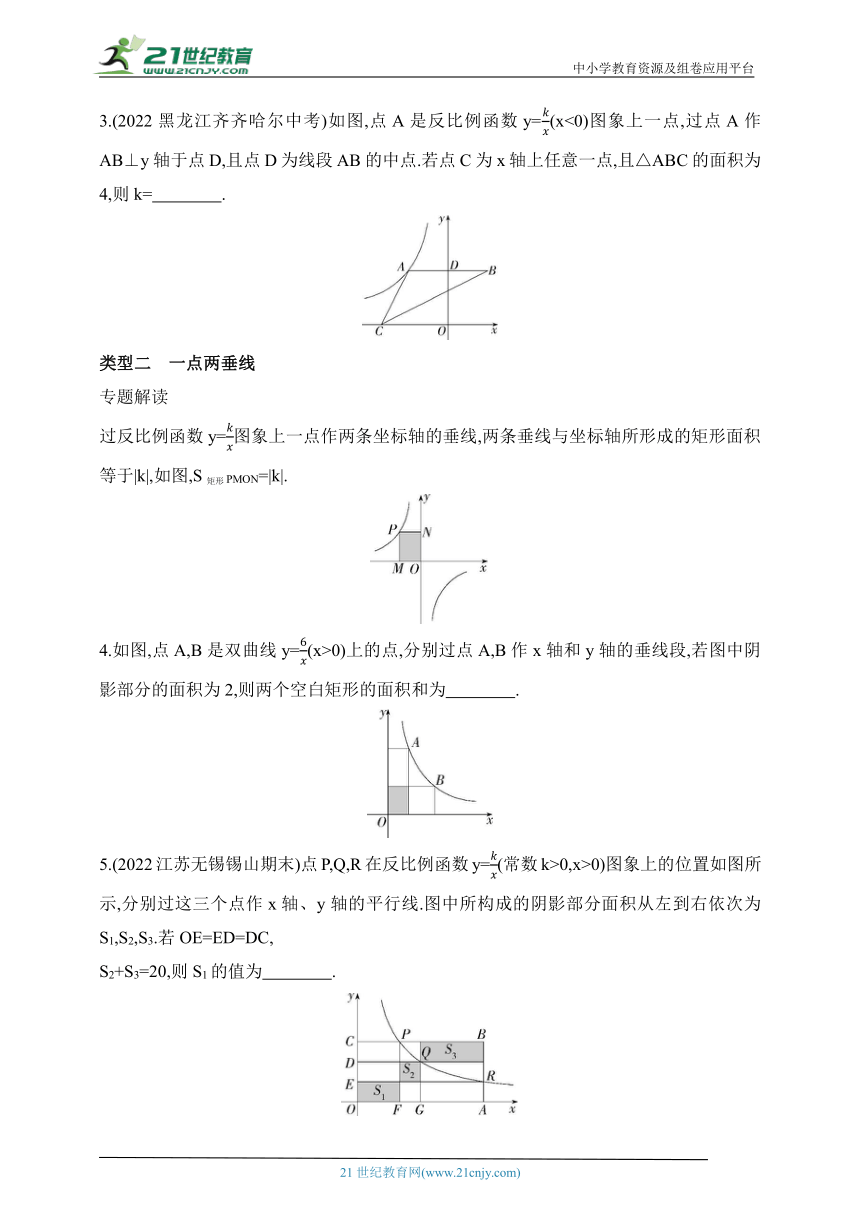
过反比例函数y=图象上一点作关于坐标轴的一条垂线,这一点和垂足及另一坐标轴上的任意一点所围成的三角形面积都等于,如图1,
PA⊥x轴,则S△PAB'=S△PAB″=S△POA=,如图2,PB⊥y轴,则S△POB=
S△PA'B=S△PA″B=.
1.(2023北京平谷期末)如图,若点A是反比例函数y=(x>0)的图象上一点,过点A作x轴的垂线交x轴于点B,点C是y轴上任意一点,则△ABC的面积为 ( )
A.1 B.2 C.3 D.4
2.(2022山东诸城期末)如图,点A在反比例函数y=的图象上,直角△OAB的面积为2,则k= .
3.(2022黑龙江齐齐哈尔中考)如图,点A是反比例函数y=(x<0)图象上一点,过点A作AB⊥y轴于点D,且点D为线段AB的中点.若点C为x轴上任意一点,且△ABC的面积为4,则k= .
类型二 一点两垂线
专题解读
过反比例函数y=图象上一点作两条坐标轴的垂线,两条垂线与坐标轴所形成的矩形面积等于|k|,如图,S矩形PMON=|k|.
4.如图,点A,B是双曲线y=(x>0)上的点,分别过点A,B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形的面积和为 .
5.(2022江苏无锡锡山期末)点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OE=ED=DC,
S2+S3=20,则S1的值为 .
类型三 两点一垂线
专题解读
反比例函数y=的图象与正比例函数图象的交点及由交点向坐标轴作垂线围成的三角形面积等于|k|,如图,S△AMB=S△ANB=|k|.
6.如图,反比例函数y=(k≠0)的图象与直线y=-3x相交于A、B两点,过点A作x轴的垂线,垂足为C,且点C的横坐标为-1,连接BC,则S△ABC= ( )
A.2 B.3 C.4 D.6
7.如图,在平面直角坐标系中,过原点O的直线交反比例函数y=(k≠0)的图象于A,B两点,BC⊥y轴于点C,△ABC的面积为6,则k的值为 .
类型四 两点两垂线
专题解读
反比例函数y=的图象与正比例函数图象的交点及由交点向坐标轴所作两条垂线所形成的图形面积等于2|k|,如图,S△APB=S四边形AMBN=2|k|.
8.如图,反比例函数y=的图象与直线y=kx(k>0)相交于A,B两点,AC∥y轴,BC∥x轴,则△ABC的面积为 .
9.如图,正比例函数y=-x与反比例函数y=(k≠0)的图象相交于A,B两点,分别过A,B两点作y轴的垂线,垂足分别为C,D,连接AD,BC,若四边形ACBD的面积为4,求反比例函数的表达式.
答案全解全析
1.A 连接OA,图略,∵AB⊥x轴,∴OC∥AB,
∴S△CAB=S△OAB===1,故选A.
2.答案 -4
解析 ∵S△AOB=2,∴=2,∴|k|=4,由图象可知k<0,∴k=-4.
3.答案 -4
解析 连接AO,如图,
∵D为AB的中点,∴AD=AB.
∵S△ABC=AB·OD,S△AOD=AD·OD,
∴S△AOD=S△ABC=2.∴=2,∴|k|=4,由图象可知k<0,∴k=-4.
4.答案 8
解析 标注字母如图所示,
∵点A、B是双曲线y=(x>0)上的点,
∴S矩形ACOG=S矩形BEOF=6,
∵S阴影=2,∴S矩形ACFD=S矩形BDGE=6-2=4,
∴S矩形ACFD+=4+4=8.
5.答案 10
解析 ∵OE=ED=DC,
∴S1=S矩形OFPC=k.
S1+S2+S3=S矩形OABC=S矩形OARE=k.
∵S2+S3=20,∴k+20=k,解得k=30,
∴S1=k=10.
6.B 将x=-1代入y=-3x,得y=3,∴A(-1,3).
把A(-1,3)代入y=,得k=-3.
∴反比例函数解析式为y=-.
∴S△AOC==.
∵点A与点B关于原点对称,∴OA=OB,
∴S△ABC=2S△AOC=2×=3.
7.答案 -6
解析 由对称性可知,OA=OB,
∴S△AOC=S△BOC=S△ABC=×6=3,
∵BC⊥y轴,∴=3,∴|k|=6,
由图象可知k<0,∴k=-6.
8.答案 10
解析 设A,则B,
∴BC=2a,AC=2×=.
∵AC∥y轴,BC∥x轴,∴AC⊥BC,
∴S△ABC=×2a×=10.
9.解析 ∵点A和点B关于原点对称,
∴OA=OB,OC=OD,AC=BD,
∴S四边形ACBD=4S△AOC=4,∴S△AOC=1.
∵S△AOC=,∴=1,∴|k|=2.
由图象可知k<0,∴k=-2,
∴反比例函数的表达式为y=-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
专项素养综合全练(一)
反比例函数中的面积问题
类型一 一点一垂线
专题解读
过反比例函数y=图象上一点作关于坐标轴的一条垂线,这一点和垂足及另一坐标轴上的任意一点所围成的三角形面积都等于,如图1,
PA⊥x轴,则S△PAB'=S△PAB″=S△POA=,如图2,PB⊥y轴,则S△POB=
S△PA'B=S△PA″B=.
1.(2023北京平谷期末)如图,若点A是反比例函数y=(x>0)的图象上一点,过点A作x轴的垂线交x轴于点B,点C是y轴上任意一点,则△ABC的面积为 ( )
A.1 B.2 C.3 D.4
2.(2022山东诸城期末)如图,点A在反比例函数y=的图象上,直角△OAB的面积为2,则k= .
3.(2022黑龙江齐齐哈尔中考)如图,点A是反比例函数y=(x<0)图象上一点,过点A作AB⊥y轴于点D,且点D为线段AB的中点.若点C为x轴上任意一点,且△ABC的面积为4,则k= .
类型二 一点两垂线
专题解读
过反比例函数y=图象上一点作两条坐标轴的垂线,两条垂线与坐标轴所形成的矩形面积等于|k|,如图,S矩形PMON=|k|.
4.如图,点A,B是双曲线y=(x>0)上的点,分别过点A,B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形的面积和为 .
5.(2022江苏无锡锡山期末)点P,Q,R在反比例函数y=(常数k>0,x>0)图象上的位置如图所示,分别过这三个点作x轴、y轴的平行线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3.若OE=ED=DC,
S2+S3=20,则S1的值为 .
类型三 两点一垂线
专题解读
反比例函数y=的图象与正比例函数图象的交点及由交点向坐标轴作垂线围成的三角形面积等于|k|,如图,S△AMB=S△ANB=|k|.
6.如图,反比例函数y=(k≠0)的图象与直线y=-3x相交于A、B两点,过点A作x轴的垂线,垂足为C,且点C的横坐标为-1,连接BC,则S△ABC= ( )
A.2 B.3 C.4 D.6
7.如图,在平面直角坐标系中,过原点O的直线交反比例函数y=(k≠0)的图象于A,B两点,BC⊥y轴于点C,△ABC的面积为6,则k的值为 .
类型四 两点两垂线
专题解读
反比例函数y=的图象与正比例函数图象的交点及由交点向坐标轴所作两条垂线所形成的图形面积等于2|k|,如图,S△APB=S四边形AMBN=2|k|.
8.如图,反比例函数y=的图象与直线y=kx(k>0)相交于A,B两点,AC∥y轴,BC∥x轴,则△ABC的面积为 .
9.如图,正比例函数y=-x与反比例函数y=(k≠0)的图象相交于A,B两点,分别过A,B两点作y轴的垂线,垂足分别为C,D,连接AD,BC,若四边形ACBD的面积为4,求反比例函数的表达式.
答案全解全析
1.A 连接OA,图略,∵AB⊥x轴,∴OC∥AB,
∴S△CAB=S△OAB===1,故选A.
2.答案 -4
解析 ∵S△AOB=2,∴=2,∴|k|=4,由图象可知k<0,∴k=-4.
3.答案 -4
解析 连接AO,如图,
∵D为AB的中点,∴AD=AB.
∵S△ABC=AB·OD,S△AOD=AD·OD,
∴S△AOD=S△ABC=2.∴=2,∴|k|=4,由图象可知k<0,∴k=-4.
4.答案 8
解析 标注字母如图所示,
∵点A、B是双曲线y=(x>0)上的点,
∴S矩形ACOG=S矩形BEOF=6,
∵S阴影=2,∴S矩形ACFD=S矩形BDGE=6-2=4,
∴S矩形ACFD+=4+4=8.
5.答案 10
解析 ∵OE=ED=DC,
∴S1=S矩形OFPC=k.
S1+S2+S3=S矩形OABC=S矩形OARE=k.
∵S2+S3=20,∴k+20=k,解得k=30,
∴S1=k=10.
6.B 将x=-1代入y=-3x,得y=3,∴A(-1,3).
把A(-1,3)代入y=,得k=-3.
∴反比例函数解析式为y=-.
∴S△AOC==.
∵点A与点B关于原点对称,∴OA=OB,
∴S△ABC=2S△AOC=2×=3.
7.答案 -6
解析 由对称性可知,OA=OB,
∴S△AOC=S△BOC=S△ABC=×6=3,
∵BC⊥y轴,∴=3,∴|k|=6,
由图象可知k<0,∴k=-6.
8.答案 10
解析 设A,则B,
∴BC=2a,AC=2×=.
∵AC∥y轴,BC∥x轴,∴AC⊥BC,
∴S△ABC=×2a×=10.
9.解析 ∵点A和点B关于原点对称,
∴OA=OB,OC=OD,AC=BD,
∴S四边形ACBD=4S△AOC=4,∴S△AOC=1.
∵S△AOC=,∴=1,∴|k|=2.
由图象可知k<0,∴k=-2,
∴反比例函数的表达式为y=-.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
