5.1 函数与它的表示法课时练(含解析)
文档属性
| 名称 | 5.1 函数与它的表示法课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 479.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第5章 对函数的再探索
5.1 函数与它的表示法
基础过关全练
知识点1 函数的表示法
1.(2023山东济南市中期中)在实验课上,小亮利用同一块木板测得小车从不同高度下滑的时间,支撑物高度h(cm)与下滑时间t(s)的关系如表:
支撑物高度h(cm) 10 20 30 40 50 …
下滑时间t(s) 3.25 3.01 2.81 2.66 2.56 …
以下结论错误的是 ( )
A.当h=40时,t=2.66
B.随支撑物高度的增加,下滑时间越来越短
C.估计当h=80时,t的值一定小于2.56
D.支撑物高度每增加10 cm,下滑时间就会减少0.24 s
2.某地海拔高度h与温度T之间的关系可用T=21-6h(温度单位:℃,海拔高度单位:km)来表示,则该地区海拔高度为2 km的山顶上的温度为
( )
A.15 ℃ B.9 ℃ C.3 ℃ D.7 ℃
【跨学科·化学】(2023山东沂水一模)张老师在化学实验室做实验时,将一杯100 ℃的水放在石棉网上自然冷却,如图所示的是这杯水冷却时的温度变化图,根据图中所显示的信息,下列说法不正确的是 ( )
A.水温从100 ℃逐渐下降到35 ℃时用了6分钟
B.从开始冷却后14分钟时的水温是15 ℃
C.实验室的室内温度是15 ℃
D.水被自然冷却到了10 ℃
知识点2 函数概念的再认识
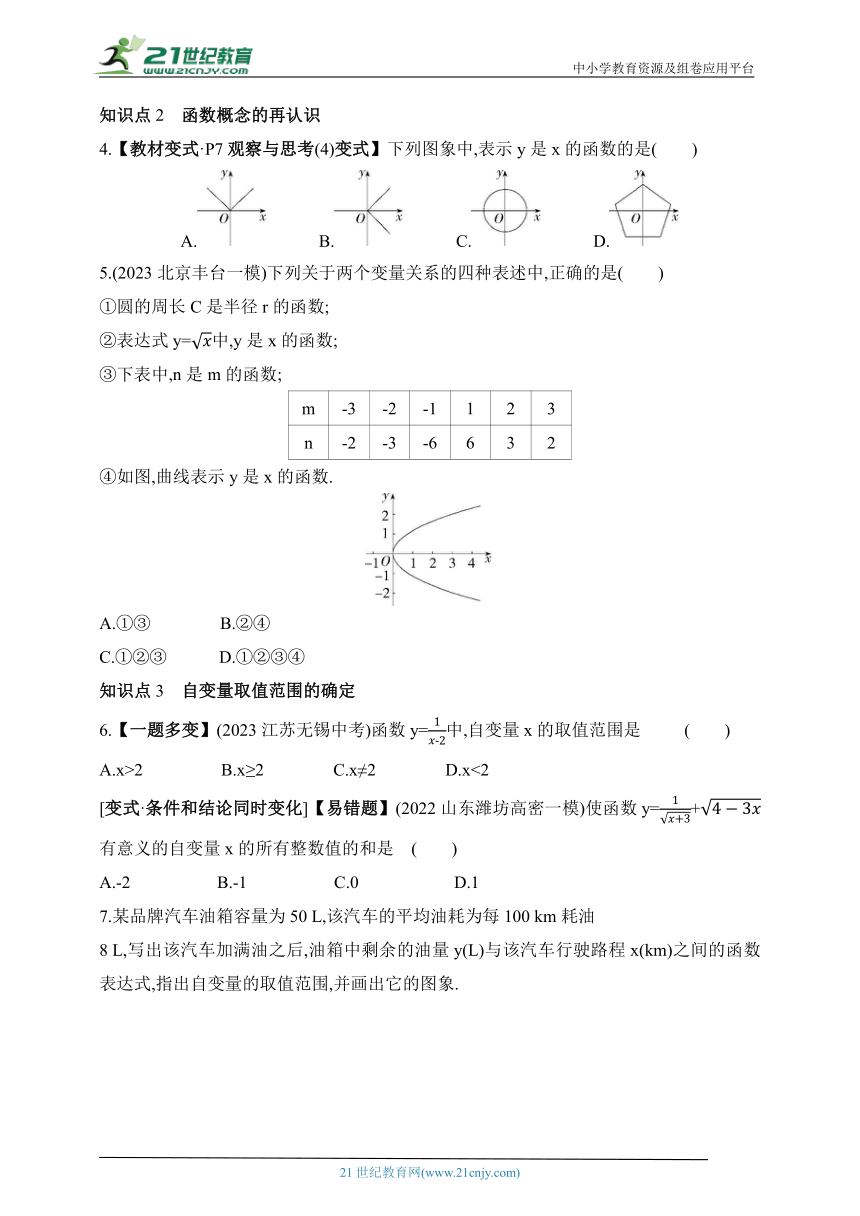
4.【教材变式·P7观察与思考(4)变式】下列图象中,表示y是x的函数的是( )
A. B. C. D.
5.(2023北京丰台一模)下列关于两个变量关系的四种表述中,正确的是( )
①圆的周长C是半径r的函数;
②表达式y=中,y是x的函数;
③下表中,n是m的函数;
m -3 -2 -1 1 2 3
n -2 -3 -6 6 3 2
④如图,曲线表示y是x的函数.
A.①③ B.②④
C.①②③ D.①②③④
知识点3 自变量取值范围的确定
6.【一题多变】(2023江苏无锡中考)函数y=中,自变量x的取值范围是 ( )
A.x>2 B.x≥2 C.x≠2 D.x<2
[变式·条件和结论同时变化]【易错题】(2022山东潍坊高密一模)使函数y=+有意义的自变量x的所有整数值的和是 ( )
A.-2 B.-1 C.0 D.1
7.某品牌汽车油箱容量为50 L,该汽车的平均油耗为每100 km耗油
8 L,写出该汽车加满油之后,油箱中剩余的油量y(L)与该汽车行驶路程x(km)之间的函数表达式,指出自变量的取值范围,并画出它的图象.
知识点4 分段函数
8.【新课标例68变式】【新独家原创】请你根据如图所示的图象编写一个符合图象所表示的函数关系的情境.
9.【中华优秀传统文化】(2023陕西榆林神木一模)9月28日为我国的“全国读书节”,以此唤醒3 000年来国民读书的热情,进一步推动中华文化在全球范围的传播,某学校为更好地创设阅读环境,营造读书氛围,拟购进一批阅读书籍,经了解,从“好学书店”购进某种书籍的本数x(本)与所需的总价钱y(元)之间的关系如图所示,根据图中的信息,解答下列问题:
(1)从“好学书店”购进该种书籍10本时,所需的总价钱为 元;
(2)当x>20时,求y与x之间的函数关系式;
(3)当购买该种书籍不超过20本时,全部按原价购买,当购买该种书籍超过20本时,超过部分是按原价的几折购买
能力提升全练
10.(2022江西中考,6,★★☆)甲、乙两种物质的溶解度y(g)与温度t(℃)之间的对应关系如图所示,则下列说法中错误的是 ( )
A.甲、乙两种物质的溶解度均随着温度的升高而增大
B.当温度升高至t2℃时,甲的溶解度比乙的溶解度大
C.当温度为0 ℃时,甲、乙的溶解度都小于20 g
D.当温度为30 ℃时,甲、乙的溶解度相等
11.【分类讨论思想】(2021山东潍坊中考,8,★★☆)记实数x1,x2,…,xn中的最小数为min|x1,x2,…,xn|,例如:min|-1,1,2|=-1,则函数y=min|2x-1,x,4-x|的图象大致为 ( )
A. B.
C. D.
12.【山东潍坊常考·多选题】(2022山东潍坊期末,12,★★☆)(多选题)荡秋千时,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图所示,下列结论正确的是 ( )
A.根据函数的定义,变量h不是关于t的函数
B.当t=0.7(s)时,h=0.5(m),表示此时秋千离地面的高度是0.5 m
C.秋千摆动第一个来回需2.8 s
D.秋千静止时离地面的高度是1 m
13.(2023重庆中考A卷,23,★★☆)如图,△ABC是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线A→B→C方向运动,点F沿折线A→C→B方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.
(1)请直接写出y关于t的函数表达式并注明自变量t的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,写出点E,F相距3个单位长度时t的值.
素养探究全练
14.【模型观念】(2023山东东阿二模)甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
(1)求a和b的值;
(2)求两车在途中相遇时t的值;
(3)当两车相距60千米时,请直接写出t的值.
答案全解全析
基础过关全练
1.D A.由题表得,当h=40时,下滑时间t=2.66,故选项A正确;B.由题表中下滑时间随支撑物高度的变化情况可知,随支撑物高度的增加,下滑时间越来越短,故选项B正确;C.结合B选项可知,当h=80时,t的值一定小于2.56,故选项C正确;D.由题表中下滑时间和支撑物高度的对应值可知,支撑物高度每增加10 cm,下滑时间不都减少0.24 s,故选项D错误,符合题意.故选D.
2.B 把h=2代入T=21-6h,得T=21-6×2=9.故选B.
3.C A.由题图可知,当t=6时,T=35,故水温从100 ℃逐渐下降到35 ℃时用了6分钟,选项A正确;B.由题图可得,从开始冷却后14分钟时的水温是15 ℃,选项B正确;C.水被自然冷却到了15 ℃时,水温继续下降,则室温肯定低于15 ℃,选项C错误,符合题意;D.水被自然冷却到了10 ℃时,水温不再下降,选项D正确.故选C.
4.A
5.C 根据函数的定义可知,①②③的表述都正确,④中当x取一个正数时,y有两个不同的值与它相对应,故④的表述错误,故选C.
6.C 由题意得x-2≠0,解得x≠2,故选C.
[变式] A 由题意得x+3>0,4-3x≥0,解得-3易错警示 易忽视分母不为0,还要注意结果是求所有整数值的和.
7.解析 8÷100=0.08(L/km),
∴油箱中剩余的油量y(L)与汽车行驶路程x(km)之间的函数表达式是y=50-0.08x.
令y=0,解得x=625.
∴y=50-0.08x(0≤x≤625),
画出图象如下:
8.解析 答案不唯一,如张老师每天上班前都到公园锻炼身体,他从家出发步行20分钟后,到达离家900米的公园,在公园锻炼了30分钟,然后他加快了速度用10分钟时间到达离家2 000米的学校.
9.解析 (1)由题图可知,购进该种书籍20本时,所需总价钱为400元,
∴购进该种书籍不超过20本时,单价为400÷20=20(元),
∴从“好学书店”购进该种书籍10本时,所需的总价钱为20×10=200(元),故答案为200.
(2)当x>20时,设y与x之间的函数关系式为y=kx+b(k≠0),易知(20,400)也满足此关系式,
把(20,400)和(50,880)代入,
得解得
∴当x>20时,y与x之间的函数关系式为y=16x+80.
(3)当x≤20时,单价为400÷20=20(元),
当x>20时,单价为(880-400)÷(50-20)=16(元),
16÷20=0.8,
∴购买该种书籍超过20本时,超过部分是按原价的八折购买.
能力提升全练
10.D A.两个函数图象从左往右都是上升的,即甲、乙两种物质的溶解度均随着温度的升高而增大,故选项A正确;B.由图象可知,当温度升高至t2℃时,甲的图象在乙的上方,故甲的溶解度比乙的溶解度大,故选项B正确;C.当t=0时,两个函数图象与y轴的交点都在20的下方,故选项C正确;D.图象上没有标出t=30的坐标,故当温度为30 ℃时,甲、乙的溶解度的大小无法判断,故选项D错误,故选D.
11.B 分别画出函数y=2x-1,y=x,y=4-x的图象,如图所示.
则函数y=min|2x-1,x,4-x|的图象大致为B.
12.BC 由图象可知,A.对于每一个摆动的时间t,h都有唯一确定的值与其对应,故变量h是关于t的函数,故选项A结论错误;B.当t=0.7(s)时,h=0.5(m),表示此时秋千离地面的高度是0.5 m,故选项B结论正确;C.秋千摆动第一个来回需要2.8 s,故选项C结论正确;D.秋千静止时离地面的高度是0.5 m,故选项D结论错误.故选BC.
13.解析 (1)y=
(2)函数图象如图.
根据函数图象可知,函数的性质为(写出其中一条即可):
①当0≤t≤4时,y随t的增大而增大;
当4②该函数在自变量的取值范围内,有最大值和最小值,
当t=4时,函数取得最大值4;
当t=0或t=6时,函数取得最小值0.
(3)当t=3或t=4.5时,点E,F相距3个单位长度.
提示:结合图象和(1)中所求表达式可知,当0≤t≤4时,若y=3,则t=3;
当4素养探究全练
14.解析 (1)a==50,b=5.5-=4.
(2)设乙车与A地的路程s与甲车离开A地的时间t之间的函数关系式为s乙=kt+m(k≠0),
将(2,0)、(5,300)代入s乙=kt+m,
得解得
∴s乙=100t-200(2≤t≤5).
当s乙=100t-200=150时,t=3.5.
故两车在途中相遇时t的值为3.5.
(3)当0≤t≤3时,s甲=50t;
当3≤t≤4时,s甲=150;
当4≤t≤5.5时,s甲=150+2×50(t-4)=100t-250.
∴s甲=
①当0≤t≤2时,令s甲=50t=60,解得t=;
②当2解得t=;
③当3≤t≤4时,s甲=150,
当t=3时,s乙=100×3-200=100,
∴s甲-s乙=150-100=50,
当t=4时,s乙=100×4-200=200,
∴s乙-s甲=200-150=50,
∴当3≤t≤4时,两车之间的最大距离为50千米;
④当4⑤当5综上所述,当两车相距60千米时,t=或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第5章 对函数的再探索
5.1 函数与它的表示法
基础过关全练
知识点1 函数的表示法
1.(2023山东济南市中期中)在实验课上,小亮利用同一块木板测得小车从不同高度下滑的时间,支撑物高度h(cm)与下滑时间t(s)的关系如表:
支撑物高度h(cm) 10 20 30 40 50 …
下滑时间t(s) 3.25 3.01 2.81 2.66 2.56 …
以下结论错误的是 ( )
A.当h=40时,t=2.66
B.随支撑物高度的增加,下滑时间越来越短
C.估计当h=80时,t的值一定小于2.56
D.支撑物高度每增加10 cm,下滑时间就会减少0.24 s
2.某地海拔高度h与温度T之间的关系可用T=21-6h(温度单位:℃,海拔高度单位:km)来表示,则该地区海拔高度为2 km的山顶上的温度为
( )
A.15 ℃ B.9 ℃ C.3 ℃ D.7 ℃
【跨学科·化学】(2023山东沂水一模)张老师在化学实验室做实验时,将一杯100 ℃的水放在石棉网上自然冷却,如图所示的是这杯水冷却时的温度变化图,根据图中所显示的信息,下列说法不正确的是 ( )
A.水温从100 ℃逐渐下降到35 ℃时用了6分钟
B.从开始冷却后14分钟时的水温是15 ℃
C.实验室的室内温度是15 ℃
D.水被自然冷却到了10 ℃
知识点2 函数概念的再认识
4.【教材变式·P7观察与思考(4)变式】下列图象中,表示y是x的函数的是( )
A. B. C. D.
5.(2023北京丰台一模)下列关于两个变量关系的四种表述中,正确的是( )
①圆的周长C是半径r的函数;
②表达式y=中,y是x的函数;
③下表中,n是m的函数;
m -3 -2 -1 1 2 3
n -2 -3 -6 6 3 2
④如图,曲线表示y是x的函数.
A.①③ B.②④
C.①②③ D.①②③④
知识点3 自变量取值范围的确定
6.【一题多变】(2023江苏无锡中考)函数y=中,自变量x的取值范围是 ( )
A.x>2 B.x≥2 C.x≠2 D.x<2
[变式·条件和结论同时变化]【易错题】(2022山东潍坊高密一模)使函数y=+有意义的自变量x的所有整数值的和是 ( )
A.-2 B.-1 C.0 D.1
7.某品牌汽车油箱容量为50 L,该汽车的平均油耗为每100 km耗油
8 L,写出该汽车加满油之后,油箱中剩余的油量y(L)与该汽车行驶路程x(km)之间的函数表达式,指出自变量的取值范围,并画出它的图象.
知识点4 分段函数
8.【新课标例68变式】【新独家原创】请你根据如图所示的图象编写一个符合图象所表示的函数关系的情境.
9.【中华优秀传统文化】(2023陕西榆林神木一模)9月28日为我国的“全国读书节”,以此唤醒3 000年来国民读书的热情,进一步推动中华文化在全球范围的传播,某学校为更好地创设阅读环境,营造读书氛围,拟购进一批阅读书籍,经了解,从“好学书店”购进某种书籍的本数x(本)与所需的总价钱y(元)之间的关系如图所示,根据图中的信息,解答下列问题:
(1)从“好学书店”购进该种书籍10本时,所需的总价钱为 元;
(2)当x>20时,求y与x之间的函数关系式;
(3)当购买该种书籍不超过20本时,全部按原价购买,当购买该种书籍超过20本时,超过部分是按原价的几折购买
能力提升全练
10.(2022江西中考,6,★★☆)甲、乙两种物质的溶解度y(g)与温度t(℃)之间的对应关系如图所示,则下列说法中错误的是 ( )
A.甲、乙两种物质的溶解度均随着温度的升高而增大
B.当温度升高至t2℃时,甲的溶解度比乙的溶解度大
C.当温度为0 ℃时,甲、乙的溶解度都小于20 g
D.当温度为30 ℃时,甲、乙的溶解度相等
11.【分类讨论思想】(2021山东潍坊中考,8,★★☆)记实数x1,x2,…,xn中的最小数为min|x1,x2,…,xn|,例如:min|-1,1,2|=-1,则函数y=min|2x-1,x,4-x|的图象大致为 ( )
A. B.
C. D.
12.【山东潍坊常考·多选题】(2022山东潍坊期末,12,★★☆)(多选题)荡秋千时,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图所示,下列结论正确的是 ( )
A.根据函数的定义,变量h不是关于t的函数
B.当t=0.7(s)时,h=0.5(m),表示此时秋千离地面的高度是0.5 m
C.秋千摆动第一个来回需2.8 s
D.秋千静止时离地面的高度是1 m
13.(2023重庆中考A卷,23,★★☆)如图,△ABC是边长为4的等边三角形,动点E,F分别以每秒1个单位长度的速度同时从点A出发,点E沿折线A→B→C方向运动,点F沿折线A→C→B方向运动,当两者相遇时停止运动.设运动时间为t秒,点E,F的距离为y.
(1)请直接写出y关于t的函数表达式并注明自变量t的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合函数图象,写出点E,F相距3个单位长度时t的值.
素养探究全练
14.【模型观念】(2023山东东阿二模)甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
(1)求a和b的值;
(2)求两车在途中相遇时t的值;
(3)当两车相距60千米时,请直接写出t的值.
答案全解全析
基础过关全练
1.D A.由题表得,当h=40时,下滑时间t=2.66,故选项A正确;B.由题表中下滑时间随支撑物高度的变化情况可知,随支撑物高度的增加,下滑时间越来越短,故选项B正确;C.结合B选项可知,当h=80时,t的值一定小于2.56,故选项C正确;D.由题表中下滑时间和支撑物高度的对应值可知,支撑物高度每增加10 cm,下滑时间不都减少0.24 s,故选项D错误,符合题意.故选D.
2.B 把h=2代入T=21-6h,得T=21-6×2=9.故选B.
3.C A.由题图可知,当t=6时,T=35,故水温从100 ℃逐渐下降到35 ℃时用了6分钟,选项A正确;B.由题图可得,从开始冷却后14分钟时的水温是15 ℃,选项B正确;C.水被自然冷却到了15 ℃时,水温继续下降,则室温肯定低于15 ℃,选项C错误,符合题意;D.水被自然冷却到了10 ℃时,水温不再下降,选项D正确.故选C.
4.A
5.C 根据函数的定义可知,①②③的表述都正确,④中当x取一个正数时,y有两个不同的值与它相对应,故④的表述错误,故选C.
6.C 由题意得x-2≠0,解得x≠2,故选C.
[变式] A 由题意得x+3>0,4-3x≥0,解得-3
7.解析 8÷100=0.08(L/km),
∴油箱中剩余的油量y(L)与汽车行驶路程x(km)之间的函数表达式是y=50-0.08x.
令y=0,解得x=625.
∴y=50-0.08x(0≤x≤625),
画出图象如下:
8.解析 答案不唯一,如张老师每天上班前都到公园锻炼身体,他从家出发步行20分钟后,到达离家900米的公园,在公园锻炼了30分钟,然后他加快了速度用10分钟时间到达离家2 000米的学校.
9.解析 (1)由题图可知,购进该种书籍20本时,所需总价钱为400元,
∴购进该种书籍不超过20本时,单价为400÷20=20(元),
∴从“好学书店”购进该种书籍10本时,所需的总价钱为20×10=200(元),故答案为200.
(2)当x>20时,设y与x之间的函数关系式为y=kx+b(k≠0),易知(20,400)也满足此关系式,
把(20,400)和(50,880)代入,
得解得
∴当x>20时,y与x之间的函数关系式为y=16x+80.
(3)当x≤20时,单价为400÷20=20(元),
当x>20时,单价为(880-400)÷(50-20)=16(元),
16÷20=0.8,
∴购买该种书籍超过20本时,超过部分是按原价的八折购买.
能力提升全练
10.D A.两个函数图象从左往右都是上升的,即甲、乙两种物质的溶解度均随着温度的升高而增大,故选项A正确;B.由图象可知,当温度升高至t2℃时,甲的图象在乙的上方,故甲的溶解度比乙的溶解度大,故选项B正确;C.当t=0时,两个函数图象与y轴的交点都在20的下方,故选项C正确;D.图象上没有标出t=30的坐标,故当温度为30 ℃时,甲、乙的溶解度的大小无法判断,故选项D错误,故选D.
11.B 分别画出函数y=2x-1,y=x,y=4-x的图象,如图所示.
则函数y=min|2x-1,x,4-x|的图象大致为B.
12.BC 由图象可知,A.对于每一个摆动的时间t,h都有唯一确定的值与其对应,故变量h是关于t的函数,故选项A结论错误;B.当t=0.7(s)时,h=0.5(m),表示此时秋千离地面的高度是0.5 m,故选项B结论正确;C.秋千摆动第一个来回需要2.8 s,故选项C结论正确;D.秋千静止时离地面的高度是0.5 m,故选项D结论错误.故选BC.
13.解析 (1)y=
(2)函数图象如图.
根据函数图象可知,函数的性质为(写出其中一条即可):
①当0≤t≤4时,y随t的增大而增大;
当4
当t=4时,函数取得最大值4;
当t=0或t=6时,函数取得最小值0.
(3)当t=3或t=4.5时,点E,F相距3个单位长度.
提示:结合图象和(1)中所求表达式可知,当0≤t≤4时,若y=3,则t=3;
当4
14.解析 (1)a==50,b=5.5-=4.
(2)设乙车与A地的路程s与甲车离开A地的时间t之间的函数关系式为s乙=kt+m(k≠0),
将(2,0)、(5,300)代入s乙=kt+m,
得解得
∴s乙=100t-200(2≤t≤5).
当s乙=100t-200=150时,t=3.5.
故两车在途中相遇时t的值为3.5.
(3)当0≤t≤3时,s甲=50t;
当3≤t≤4时,s甲=150;
当4≤t≤5.5时,s甲=150+2×50(t-4)=100t-250.
∴s甲=
①当0≤t≤2时,令s甲=50t=60,解得t=;
②当2
③当3≤t≤4时,s甲=150,
当t=3时,s乙=100×3-200=100,
∴s甲-s乙=150-100=50,
当t=4时,s乙=100×4-200=200,
∴s乙-s甲=200-150=50,
∴当3≤t≤4时,两车之间的最大距离为50千米;
④当4
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
