5.2.4 反比例函数课时练(含解析)
文档属性
| 名称 | 5.2.4 反比例函数课时练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 436.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 20:36:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第5章 对函数的再探索
5.2 反比例函数
第4课时 反比例函数的应用
基础过关全练
知识点6 反比例函数在实际问题中的应用
22.【跨学科·物理】(2023山东菏泽牡丹二模)由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值R(始终保持R>0),发现通过滑动变阻器的电流I与滑动变阻器的电阻R成反比例函数关系,它的图象如图所示,若使得通过滑动变阻器的电流不超过4 A,则滑动变阻器阻值的范围是 .
23.(2023江苏扬州中考)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=3(m3)时,p=8 000(Pa).当气球内的气体压强大于40 000 Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 m3.
24.【教材变式·P23例6】(2023山东青岛莱西二模)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(h)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象求出血液中药物浓度下降阶段y关于x的函数表达式;
(2)血液中药物浓度不低于5微克/毫升的持续时间为多少小时
能力提升全练
25.(2023山东泰安中考,8,★★☆)一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是 ( )
A. B. C. D.
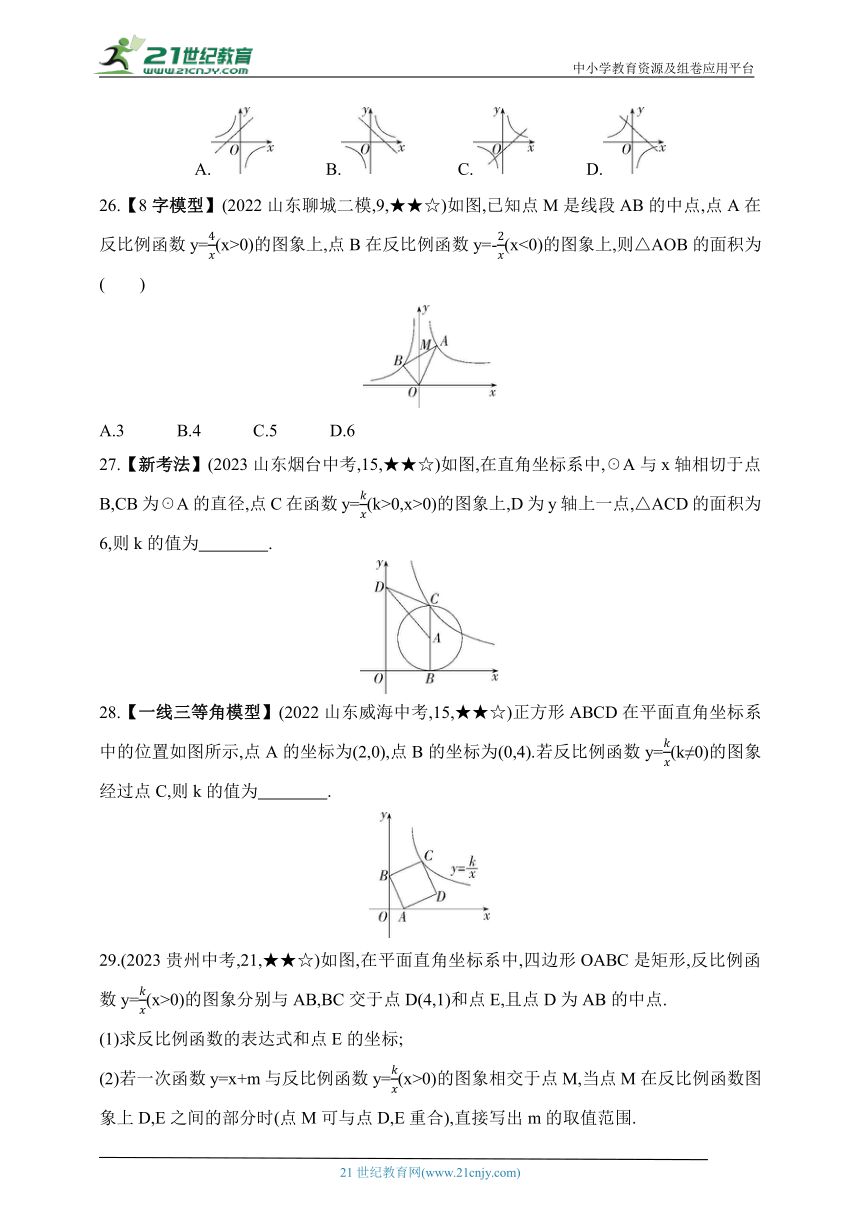
26.【8字模型】(2022山东聊城二模,9,★★☆)如图,已知点M是线段AB的中点,点A在反比例函数y=(x>0)的图象上,点B在反比例函数y=-(x<0)的图象上,则△AOB的面积为 ( )
A.3 B.4 C.5 D.6
27.【新考法】(2023山东烟台中考,15,★★☆)如图,在直角坐标系中,☉A与x轴相切于点B,CB为☉A的直径,点C在函数y=(k>0,x>0)的图象上,D为y轴上一点,△ACD的面积为6,则k的值为 .
28.【一线三等角模型】(2022山东威海中考,15,★★☆)正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 .
29.(2023贵州中考,21,★★☆)如图,在平面直角坐标系中,四边形OABC是矩形,反比例函数y=(x>0)的图象分别与AB,BC交于点D(4,1)和点E,且点D为AB的中点.
(1)求反比例函数的表达式和点E的坐标;
(2)若一次函数y=x+m与反比例函数y=(x>0)的图象相交于点M,当点M在反比例函数图象上D,E之间的部分时(点M可与点D,E重合),直接写出m的取值范围.
30.【和差法求面积】(2023山东聊城中考,23,★★☆)如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(-1,4),B(a,-1)两点.
(1)求反比例函数和一次函数的表达式;
(2)点P(n,0)在x轴负半轴上,连接AP,过点B作BQ∥AP,交y=的图象于点Q,连接PQ.当BQ=AP时,若四边形APQB的面积为36,求n的值.
31.【新考法】(2023河南中考,19,★★☆)小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数y=图象上的点A(,1)和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作,连接BF.
(1)求k的值;
(2)求扇形AOC的半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
素养探究全练
32.【模型观念】(2023山东菏泽中考)如图,已知坐标轴上两点A(0,4),B(2,0),连接AB,过点B作BC⊥AB,交反比例函数y=在第一象限的图象于点C(a,1).
(1)求反比例函数y=和直线OC的表达式;
(2)将直线OC向上平移个单位,得到直线l,求直线l与反比例函数图象的交点坐标.
答案全解全析
基础过关全练
22.答案 R≥2
解析 由图象可知,当电流I=4(A)时,电阻R=2(Ω),∴当I≤4时,R≥2.
23.答案 0.6
解析 设气球内气体的压强p(Pa)与气球体积V(m3)之间的函数解析式为p=(k≠0),
∵当V=3(m3)时,p=8 000(Pa),∴k=Vp=24 000,∴p=,
当p=40 000(Pa)时,V==0.6(m3),
∵气球内的气压大于40 000 Pa时,气球将爆炸,且p随V的增大而减小,∴为确保气球不爆炸,气球的体积应不小于0.6 m3.
24.解析 (1)当4≤x≤10时,设反比例函数表达式为y=(k≠0),将(4,10)代入得10=,解得k=40,
∴血液中药物浓度下降阶段y关于x的函数表达式为y=(4≤x≤10).
(2)当0≤x<4时,设直线表达式为y=ax(a≠0),
易知(4,10)也满足此表达式,
将(4,10)代入得10=4a,解得a=,
∴当0≤x<4时,y=x,
将y=5代入得5=x,解得x=2,
将y=5代入y=,得5=,解得x=8,
∵8-2=6(小时),
∴血液中药物浓度不低于5微克/毫升的持续时间为6小时.
能力提升全练
25.D 选项A:一次函数图象经过第一、二、三象限,则a>0,b>0,所以ab>0,则反比例函数的图象应该位于第一、三象限,选项A错误;选项B和D:一次函数的图象经过第一、二、四象限,则a<0,b>0,所以ab<0,则反比例函数的图象应该位于第二、四象限,选项B错误,选项D正确;选项C:一次函数的图象经过第一、三、四象限,则a>0,b<0,所以ab<0,则反比例函数的图象应该位于第二、四象限,选项C错误.故选D.
26.A 如图,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,
则AC∥BD,∠BDM=∠ACM=90°,∴∠MAC=∠MBD,
∵M是线段AB的中点,∴AM=BM,∴△ACM≌△BDM,
∴S△AOB=S△BOD+S△AOC=+=1+2=3.故选A.
方法解读 本题属于“8”字模型,分别过点A、B作y轴的垂线,构造一组“8”字形全等三角形,从而转化为求两个直角三角形的面积和.
27.答案 24
解析 如图,连接BD、OC,
∵BC为☉A的直径,∴BC=2AC,
∴S△BDC=2S△ACD=2×6=12.
∵☉A与x轴相切于点B,CB为直径,
∴CB⊥x轴,∴CB∥y轴,∴△BDC和△OBC同底等高,
∴S△OBC=S△BDC=12.∴=12,∴|k|=24,
∵k>0,∴k=24.
28.答案 24
解析 如图,过C作CE⊥y轴于E,
∵B(0,4),A(2,0),∴OB=4,OA=2,
∵四边形ABCD为正方形,∴∠CBA=90°,AB=BC,
∴∠CBE+∠ABO=90°,
∵∠BAO+∠ABO=90°,∴∠CBE=∠BAO,
又∵∠CEB=∠BOA=90°,∴△ABO≌△BCE.
∴OA=BE=2,OB=CE=4,∴OE=OB+BE=6,
∴C(4,6),将C(4,6)代入y=可得,k=24.
方法解读 本题属于同侧一线三等角模型,过点C作CE⊥y轴,构造△BCE≌△ABO,从而求出点C的坐标.
29.解析 (1)把(4,1)代入y=,得1=,解得k=4,
∴反比例函数的表达式为y=.
∵点A在x轴上,点D的纵坐标为1,D为AB的中点,
∴点B的纵坐标为2.
又BE∥x轴,∴点E的纵坐标为2.
设点E的横坐标为a,则2a=4,解得a=2,
∴点E的坐标为(2,2).
(2)-3≤m≤0.
详解:当点M与点D重合时,
把(4,1)代入y=x+m,得1=4+m,解得m=-3.
当点M与点E重合时,
把(2,2)代入y=x+m,得2=2+m,解得m=0.
∴m的取值范围为-3≤m≤0.
30.解析 (1)将A(-1,4)代入y=得,4=,
解得m=-4,∴反比例函数的表达式为y=-.
将B(a,-1)代入y=-得,a=4,∴B(4,-1).
将A、B两点坐标代入y=kx+b得,
解得
∴一次函数的表达式为y=-x+3.
(2)连接PB,设AB与x轴交于点M,如图,
y=-x+3中,令y=0,得x=3,
∴M(3,0),∴PM=3-n.
∵BQ∥AP,BQ=AP,
∴四边形APQB是平行四边形.
∴S△APB=S APQB=×36=18.
又S△APB=S△APM+S△BPM,
∴×(3-n)×4+×(3-n)×1=18,解得n=-.
31.解析 本题将菱形、扇形的知识融合到反比例函数中进行考查.
(1)将A(,1)代入到y=中,
得1=,解得k=.
(2)如图,连接AC交x轴于点G,
∵四边形AOCD为菱形,∴AC⊥OD,OD平分∠AOC.
在Rt△AOG中,
OA==2,tan∠AOD==,
∴∠AOD=30°,∴∠AOC=2×30°=60°.
∴扇形AOC的半径为2,圆心角的度数为60°.
(3)3-π.
详解:如图,设OE与BF交于点H,则S△OHB=,
∴S△OFB=2×=.
∵S△OAG=,∴S菱形AOCD=4×=2.
∵==π,
∴S阴影=S△OBF+S菱形AOCD-S扇形AOC
=+2-π=3-π.
素养探究全练
32.解析 (1)如图,过点C作CD⊥x轴于点D,
∵∠AOB=90°,
∴∠BDC=∠AOB=90°,
∵BC⊥AB,
∴∠ABO+∠CBD=90°,
∵∠ABO+∠BAO=90°,
∴∠CBD=∠BAO,
∴△CBD∽△BAO,∴=,
∵A(0,4),B(2,0),C(a,1),
∴AO=4,BO=2,CD=1,BD=a-2.∴=,
解得a=4,∴点C的坐标是(4,1),
把C(4,1)代入y=中,得1=,∴k=4,
∴反比例函数的表达式为y=.
设直线OC的表达式为y=mx(m≠0),
∵直线OC经过点C(4,1),∴4m=1,解得m=,
∴直线OC的表达式为y=x.
(2)将直线OC向上平移个单位,得到直线l,
∴直线l的表达式为y=x+,
联立解得
∴直线l与反比例函数图象的交点坐标为,(2,2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第5章 对函数的再探索
5.2 反比例函数
第4课时 反比例函数的应用
基础过关全练
知识点6 反比例函数在实际问题中的应用
22.【跨学科·物理】(2023山东菏泽牡丹二模)由电源、开关、滑动变阻器及若干导线组成的串联电路中,已知电源电压为定值,闭合开关后,改变滑动变阻器的阻值R(始终保持R>0),发现通过滑动变阻器的电流I与滑动变阻器的电阻R成反比例函数关系,它的图象如图所示,若使得通过滑动变阻器的电流不超过4 A,则滑动变阻器阻值的范围是 .
23.(2023江苏扬州中考)某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=3(m3)时,p=8 000(Pa).当气球内的气体压强大于40 000 Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于 m3.
24.【教材变式·P23例6】(2023山东青岛莱西二模)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x(h)之间的函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象求出血液中药物浓度下降阶段y关于x的函数表达式;
(2)血液中药物浓度不低于5微克/毫升的持续时间为多少小时
能力提升全练
25.(2023山东泰安中考,8,★★☆)一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是 ( )
A. B. C. D.
26.【8字模型】(2022山东聊城二模,9,★★☆)如图,已知点M是线段AB的中点,点A在反比例函数y=(x>0)的图象上,点B在反比例函数y=-(x<0)的图象上,则△AOB的面积为 ( )
A.3 B.4 C.5 D.6
27.【新考法】(2023山东烟台中考,15,★★☆)如图,在直角坐标系中,☉A与x轴相切于点B,CB为☉A的直径,点C在函数y=(k>0,x>0)的图象上,D为y轴上一点,△ACD的面积为6,则k的值为 .
28.【一线三等角模型】(2022山东威海中考,15,★★☆)正方形ABCD在平面直角坐标系中的位置如图所示,点A的坐标为(2,0),点B的坐标为(0,4).若反比例函数y=(k≠0)的图象经过点C,则k的值为 .
29.(2023贵州中考,21,★★☆)如图,在平面直角坐标系中,四边形OABC是矩形,反比例函数y=(x>0)的图象分别与AB,BC交于点D(4,1)和点E,且点D为AB的中点.
(1)求反比例函数的表达式和点E的坐标;
(2)若一次函数y=x+m与反比例函数y=(x>0)的图象相交于点M,当点M在反比例函数图象上D,E之间的部分时(点M可与点D,E重合),直接写出m的取值范围.
30.【和差法求面积】(2023山东聊城中考,23,★★☆)如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(-1,4),B(a,-1)两点.
(1)求反比例函数和一次函数的表达式;
(2)点P(n,0)在x轴负半轴上,连接AP,过点B作BQ∥AP,交y=的图象于点Q,连接PQ.当BQ=AP时,若四边形APQB的面积为36,求n的值.
31.【新考法】(2023河南中考,19,★★☆)小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数y=图象上的点A(,1)和点B为顶点,分别作菱形AOCD和菱形OBEF,点D,E在x轴上,以点O为圆心,OA长为半径作,连接BF.
(1)求k的值;
(2)求扇形AOC的半径及圆心角的度数;
(3)请直接写出图中阴影部分面积之和.
素养探究全练
32.【模型观念】(2023山东菏泽中考)如图,已知坐标轴上两点A(0,4),B(2,0),连接AB,过点B作BC⊥AB,交反比例函数y=在第一象限的图象于点C(a,1).
(1)求反比例函数y=和直线OC的表达式;
(2)将直线OC向上平移个单位,得到直线l,求直线l与反比例函数图象的交点坐标.
答案全解全析
基础过关全练
22.答案 R≥2
解析 由图象可知,当电流I=4(A)时,电阻R=2(Ω),∴当I≤4时,R≥2.
23.答案 0.6
解析 设气球内气体的压强p(Pa)与气球体积V(m3)之间的函数解析式为p=(k≠0),
∵当V=3(m3)时,p=8 000(Pa),∴k=Vp=24 000,∴p=,
当p=40 000(Pa)时,V==0.6(m3),
∵气球内的气压大于40 000 Pa时,气球将爆炸,且p随V的增大而减小,∴为确保气球不爆炸,气球的体积应不小于0.6 m3.
24.解析 (1)当4≤x≤10时,设反比例函数表达式为y=(k≠0),将(4,10)代入得10=,解得k=40,
∴血液中药物浓度下降阶段y关于x的函数表达式为y=(4≤x≤10).
(2)当0≤x<4时,设直线表达式为y=ax(a≠0),
易知(4,10)也满足此表达式,
将(4,10)代入得10=4a,解得a=,
∴当0≤x<4时,y=x,
将y=5代入得5=x,解得x=2,
将y=5代入y=,得5=,解得x=8,
∵8-2=6(小时),
∴血液中药物浓度不低于5微克/毫升的持续时间为6小时.
能力提升全练
25.D 选项A:一次函数图象经过第一、二、三象限,则a>0,b>0,所以ab>0,则反比例函数的图象应该位于第一、三象限,选项A错误;选项B和D:一次函数的图象经过第一、二、四象限,则a<0,b>0,所以ab<0,则反比例函数的图象应该位于第二、四象限,选项B错误,选项D正确;选项C:一次函数的图象经过第一、三、四象限,则a>0,b<0,所以ab<0,则反比例函数的图象应该位于第二、四象限,选项C错误.故选D.
26.A 如图,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,
则AC∥BD,∠BDM=∠ACM=90°,∴∠MAC=∠MBD,
∵M是线段AB的中点,∴AM=BM,∴△ACM≌△BDM,
∴S△AOB=S△BOD+S△AOC=+=1+2=3.故选A.
方法解读 本题属于“8”字模型,分别过点A、B作y轴的垂线,构造一组“8”字形全等三角形,从而转化为求两个直角三角形的面积和.
27.答案 24
解析 如图,连接BD、OC,
∵BC为☉A的直径,∴BC=2AC,
∴S△BDC=2S△ACD=2×6=12.
∵☉A与x轴相切于点B,CB为直径,
∴CB⊥x轴,∴CB∥y轴,∴△BDC和△OBC同底等高,
∴S△OBC=S△BDC=12.∴=12,∴|k|=24,
∵k>0,∴k=24.
28.答案 24
解析 如图,过C作CE⊥y轴于E,
∵B(0,4),A(2,0),∴OB=4,OA=2,
∵四边形ABCD为正方形,∴∠CBA=90°,AB=BC,
∴∠CBE+∠ABO=90°,
∵∠BAO+∠ABO=90°,∴∠CBE=∠BAO,
又∵∠CEB=∠BOA=90°,∴△ABO≌△BCE.
∴OA=BE=2,OB=CE=4,∴OE=OB+BE=6,
∴C(4,6),将C(4,6)代入y=可得,k=24.
方法解读 本题属于同侧一线三等角模型,过点C作CE⊥y轴,构造△BCE≌△ABO,从而求出点C的坐标.
29.解析 (1)把(4,1)代入y=,得1=,解得k=4,
∴反比例函数的表达式为y=.
∵点A在x轴上,点D的纵坐标为1,D为AB的中点,
∴点B的纵坐标为2.
又BE∥x轴,∴点E的纵坐标为2.
设点E的横坐标为a,则2a=4,解得a=2,
∴点E的坐标为(2,2).
(2)-3≤m≤0.
详解:当点M与点D重合时,
把(4,1)代入y=x+m,得1=4+m,解得m=-3.
当点M与点E重合时,
把(2,2)代入y=x+m,得2=2+m,解得m=0.
∴m的取值范围为-3≤m≤0.
30.解析 (1)将A(-1,4)代入y=得,4=,
解得m=-4,∴反比例函数的表达式为y=-.
将B(a,-1)代入y=-得,a=4,∴B(4,-1).
将A、B两点坐标代入y=kx+b得,
解得
∴一次函数的表达式为y=-x+3.
(2)连接PB,设AB与x轴交于点M,如图,
y=-x+3中,令y=0,得x=3,
∴M(3,0),∴PM=3-n.
∵BQ∥AP,BQ=AP,
∴四边形APQB是平行四边形.
∴S△APB=S APQB=×36=18.
又S△APB=S△APM+S△BPM,
∴×(3-n)×4+×(3-n)×1=18,解得n=-.
31.解析 本题将菱形、扇形的知识融合到反比例函数中进行考查.
(1)将A(,1)代入到y=中,
得1=,解得k=.
(2)如图,连接AC交x轴于点G,
∵四边形AOCD为菱形,∴AC⊥OD,OD平分∠AOC.
在Rt△AOG中,
OA==2,tan∠AOD==,
∴∠AOD=30°,∴∠AOC=2×30°=60°.
∴扇形AOC的半径为2,圆心角的度数为60°.
(3)3-π.
详解:如图,设OE与BF交于点H,则S△OHB=,
∴S△OFB=2×=.
∵S△OAG=,∴S菱形AOCD=4×=2.
∵==π,
∴S阴影=S△OBF+S菱形AOCD-S扇形AOC
=+2-π=3-π.
素养探究全练
32.解析 (1)如图,过点C作CD⊥x轴于点D,
∵∠AOB=90°,
∴∠BDC=∠AOB=90°,
∵BC⊥AB,
∴∠ABO+∠CBD=90°,
∵∠ABO+∠BAO=90°,
∴∠CBD=∠BAO,
∴△CBD∽△BAO,∴=,
∵A(0,4),B(2,0),C(a,1),
∴AO=4,BO=2,CD=1,BD=a-2.∴=,
解得a=4,∴点C的坐标是(4,1),
把C(4,1)代入y=中,得1=,∴k=4,
∴反比例函数的表达式为y=.
设直线OC的表达式为y=mx(m≠0),
∵直线OC经过点C(4,1),∴4m=1,解得m=,
∴直线OC的表达式为y=x.
(2)将直线OC向上平移个单位,得到直线l,
∴直线l的表达式为y=x+,
联立解得
∴直线l与反比例函数图象的交点坐标为,(2,2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
