5.4.3 二次函数的图象和性质课时练(含解析)
文档属性
| 名称 | 5.4.3 二次函数的图象和性质课时练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 390.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 20:40:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第5章 对函数的再探索
5.4 二次函数的图象和性质
第3课时 二次函数y=a(x-h)2+k和y=ax2+bx+c的图象和性质
基础过关全练
知识点4 二次函数y=a(x-h)2+k的图象和性质及图象的平移规律
18.(2023甘肃兰州中考)已知二次函数y=-3(x-2)2-3,下列说法正确的是( )
A.图象的对称轴为直线x=-2 B.图象的顶点坐标为(2,3)
C.函数的最大值是-3 D.函数的最小值是-3
19.(2023江苏徐州中考)在平面直角坐标系中,将二次函数y=(x+1)2+3的图象向右平移2个单位长度,再向下平移1个单位长度,所得抛物线对应的函数表达式为 ( )
A.y=(x+3)2+2 B.y=(x-1)2+2
C.y=(x-1)2+4 D.y=(x+3)2+4
20.(2020江苏南京中考)下列关于二次函数y=-(x-m)2+m2+1(m为常数)的结论:①该函数的图象与函数y=-x2的图象形状相同;②该函数的图象一定经过点(0,1);③当x>0时,y随x的增大而减小;④该函数的图象的顶点在函数y=x2+1的图象上.其中所有正确结论的序号是 .
知识点5 二次函数y=ax2+bx+c的图象和性质
21.(2022山东淄博临淄期末)二次函数y=-x2-(k-4)x+6中,当x>-2时,y随着x的增大而减小,当x<-2时,y随着x的增大而增大,则k的值为 ( )
A.-8 B.-4 C.4 D.8
22.(2023山东青州期末)对于二次函数y=x2+4x+5的图象,下列说法不正确的是( )
A.开口向上 B.对称轴是直线x=2
C.顶点坐标是(-2,1) D.与x轴没有交点
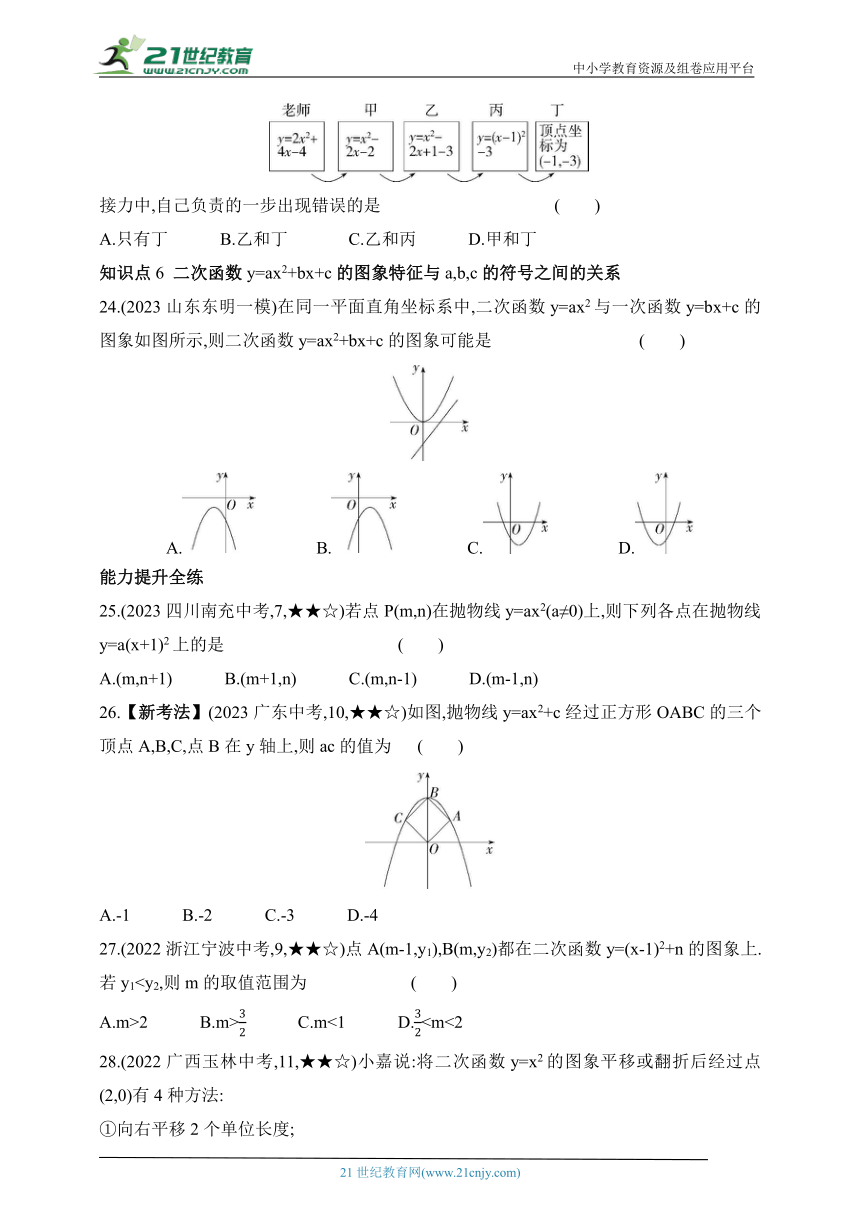
23.【新考法】(2022山东菏泽牡丹一模)老师设计了接力游戏,用合作的方式完成“求抛物线y=2x2+4x-4的顶点坐标”,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
接力中,自己负责的一步出现错误的是 ( )
A.只有丁 B.乙和丁 C.乙和丙 D.甲和丁
知识点6 二次函数y=ax2+bx+c的图象特征与a,b,c的符号之间的关系
24.(2023山东东明一模)在同一平面直角坐标系中,二次函数y=ax2与一次函数y=bx+c的图象如图所示,则二次函数y=ax2+bx+c的图象可能是 ( )
A. B. C. D.
能力提升全练
25.(2023四川南充中考,7,★★☆)若点P(m,n)在抛物线y=ax2(a≠0)上,则下列各点在抛物线y=a(x+1)2上的是 ( )
A.(m,n+1) B.(m+1,n) C.(m,n-1) D.(m-1,n)
26.【新考法】(2023广东中考,10,★★☆)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为 ( )
A.-1 B.-2 C.-3 D.-4
27.(2022浙江宁波中考,9,★★☆)点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上.若y1A.m>2 B.m> C.m<1 D.28.(2022广西玉林中考,11,★★☆)小嘉说:将二次函数y=x2的图象平移或翻折后经过点(2,0)有4种方法:
①向右平移2个单位长度;
②向右平移1个单位长度,再向下平移1个单位长度;
③向下平移4个单位长度;
④沿x轴翻折,再向上平移4个单位长度.
你认为小嘉说的方法中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
29.(2023江苏扬州中考,8,★★☆)已知二次函数y=ax2-2x+(a为常数,且a>0),下列结论:①函数图象一定经过第一、二、四象限;②函数图象一定不经过第三象限;③当x<0时,y随x的增大而减小;④当x>0时,y随x的增大而增大.其中所有正确结论的序号是 ( )
A.①② B.②③ C.② D.③④
30.(2023浙江台州中考,10,★★☆)抛物线y=ax2-a(a≠0)与直线y=kx交于A(x1,y1),B(x2,y2)两点,若x1+x2<0,则直线y=ax+k一定经过 ( )
A.第一、二象限 B.第二、三象限
C.第三、四象限 D.第一、四象限
31.【排除法】(2022湖南株洲中考,10,★★☆)已知二次函数y=ax2+bx-c(a≠0),其中b>0,c>0,则该函数的图象可能为( )
A. B.
C. D.
32.(2023山东济南莱芜二模,10,★★☆)在平面直角坐标系中,若点M(x1,y1),N(x2,y2)(x10)上的两点,且满足x1+x2=4时,都有y1>y2,则m的取值范围是( )
A.0C.m> D.33.【山东潍坊常考·多选题】(2023山东青州二模,9,★★☆)(多选题)已知二次函数的表达式为y=-x2-2x+3,将其图象向右平移k(k>0)个单位,得到新的二次函数y1的图象,使得当-1A.4 B.5 C.6 D.7
34.【山东潍坊常考·多选题】(2023山东潍坊三模,9,★★☆)(多选题)如图,抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,则下列结论正确的是 ( )
A.abc>0 B.a+b+c>0 C.3b<2c D.b>a+c
35.(2023福建中考,16,★★☆)已知抛物线y=ax2-2ax+b(a>0)经过A(2n+3,y1),B(n-1,y2)两点,若A,B分别位于抛物线对称轴的两侧,且y136.【将军饮马模型】(2019山东潍坊中考,17,★★☆)如图,直线y=x+1与抛物线y=x2-4x+5交于A,B两点,点P是y轴上的一个动点,当△PAB的周长最小时,S△PAB= .
素养探究全练
37.【模型观念】(2022河北中考)如图,点P(a,3)在抛物线C:y=4-(6-x)2上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上画出点P及C的一段,分别记为P',C'.平移该胶片,使C'所在抛物线对应的函数解析式恰为y=-x2+6x-9.求点P'移动的最短路程.
答案全解全析
基础过关全练
18.C 二次函数y=-3(x-2)2-3的图象的开口向下,对称轴为直线x=2,顶点坐标为(2,-3),当x=2时,y有最大值,为-3,故选C.
19.B 将二次函数y=(x+1)2+3的图象向右平移2个单位长度,再向下平移1个单位长度,所得抛物线对应的函数表达式为y=(x+1-2)2+3-1,即y=(x-1)2+2.故选B.
20.答案 ①②④
解析 ∵二次函数y=-(x-m)2+m2+1(m为常数)与函数y=-x2的二次项系数都为-1,∴两函数图象的形状相同,故结论①正确;在函数y=-(x-m)2+m2+1中,令x=0,得y=-m2+m2+1=1,∴该函数的图象一定经过点(0,1),故结论②正确;由解析式可得抛物线开口向下,对称轴为直线x=m,当x>m时,y随x的增大而减小,故结论③错误;∵抛物线开口向下,∴当x=m时,函数y有最大值,为m2+1,∴该函数图象的顶点在函数y=x2+1的图象上,故结论④正确.综上,正确的结论为①②④.
21.D 由题意可知,抛物线对称轴为直线x=-2,
∴-=-2,解得k=8.
22.B ∵y=x2+4x+5=(x+2)2+1,∴抛物线开口向上,对称轴是直线x=-2,顶点坐标是(-2,1),故A,C选项正确,B选项错误,∵顶点在第二象限,抛物线开口向上,∴抛物线与x轴没有交点,故D选项正确.故选B.
23.D 本题通过接力游戏的方式让学生学会将二次函数的一般式化为顶点式,题目中同时呈现了错例,增强学习效果.甲的运算应为y=2x2+4x-4=2(x2+2x-2);乙和丙的运算正确;由丙的结果可知顶点坐标为(1,-3),所以出现错误的是甲和丁.故选D.
24.D 观察函数图象可知,a>0,b>0,c<0,∴-<0,∴二次函数y=ax2+bx+c的图象开口向上,对称轴在y轴左侧,与y轴的交点在y轴负半轴上.故选D.
能力提升全练
25.D ∵点P(m,n)在抛物线y=ax2(a≠0)上,
∴n=am2,∴二次函数y=a(x+1)2(a≠0)中,当x+1=m时,y=n,此时x=m-1,即当x=m-1时,y=n,
∴点(m-1,n)在抛物线y=a(x+1)2上,故选D.
26.B 本题结合正方形的性质考查字母系数之间的关系.
如图,连接AC,交OB于点E,
∵四边形OABC是正方形,∴OE=AE=OB.
由题意可知B(0,c),∴A.
将A点坐标代入y=ax2+c得=a·+c.
化简得ac2=-2c.∵c≠0,∴ac=-2,故选B.
27.B ∵点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上,
∴y1=(m-1-1)2+n=(m-2)2+n,y2=(m-1)2+n,
∵y1∴(m-2)2-(m-1)2<0,即-2m+3<0,
∴m>,故选B.
28.D 此类题目一般考查平移后函数的图象,本题考查通过四种不同的平移方法看图象是否经过点(2,0).①将二次函数y=x2的图象向右平移2个单位长度得到y=(x-2)2的图象,当x=2时,y=(2-2)2=0,故①正确;
②将二次函数y=x2的图象向右平移1个单位长度,再向下平移1个单位长度得到y=(x-1)2-1的图象,当x=2时,y=(2-1)2-1=0,故②正确;
③将二次函数y=x2的图象向下平移4个单位长度得到y=x2-4的图象,当x=2时,y=22-4=0,故③正确;
④将二次函数y=x2的图象沿x轴翻折,再向上平移4个单位长度得到y=-x2+4的图象,当x=2时,y=-22+4=0,故④正确.
综上所述,正确的个数为4.故选D.
29.B ∵a>0,b=-2<0,c=>0,
∴抛物线开口向上,对称轴在y轴右侧,与y轴的交点在y轴正半轴上.
∴图象一定经过第一、二象限,一定不经过第三象限,可能经过第四象限,故①错误,②正确.
∵抛物线开口向上,对称轴在y轴右侧,
∴当x<0时,y随x的增大而减小,故③正确;当x>0时,图象先下降后上升,故④错误.综上,正确结论的序号是②③,故选B.
30.D ∵抛物线y=ax2-a(a≠0)与直线y=kx交于A(x1,y1),B(x2,y2)两点,∴kx=ax2-a,
∴ax2-kx-a=0,∴x1+x2=,∵x1+x2<0,
∴<0,∴a,k异号.
①当a>0,k<0时,直线y=ax+k经过第一、三、四象限,
②当a<0,k>0时,直线y=ax+k经过第一、二、四象限,
综上,直线y=ax+k一定经过第一、四象限.故选D.
31.C 对于二次函数y=ax2+bx-c(a≠0),
令x=0,则y=-c,
∴抛物线与y轴的交点坐标为(0,-c),
∵c>0,∴-c<0,
∴抛物线与y轴的交点在y轴的负半轴上,
可以排除A选项和D选项;
B选项和C选项中,抛物线的对称轴为直线x=->0,∵b>0,∴a<0,
∴抛物线开口向下,可以排除B选项.故选C.
方法解读 本题需用排除法找出符合条件的函数图象,先根据c的符号确定抛物线与y轴的交点可排除两个选项,再根据对称轴的位置排除一个错误选项,剩余的即为可能的函数图象.
32.A 由y1>y2可得,(m-2x1+m)-(m-2x2+m)>0,
整理,得(x1-x2)[m(x1+x2)-2]>0,
∵x1+x2=4,∴(x1-x2)(4m-2)>0,
∵x1解得m<,∴033.AB ∵y=-x2-2x+3=-(x+1)2+4,
∴二次函数y=-x2-2x+3的图象向右平移k(k>0)个单位得到y1=-(x+1-k)2+4的图象,
∴函数y1的图象的对称轴为直线x=k-1,
∵当-1∴3≤k-1≤4,解得4≤k≤5,
故A、B选项符合题意,故选AB.
34.AC 由图象得a>0,c<0,-=1,∴b=-2a<0,
∴abc>0,故A正确;
由图象可知,当x=1时,y<0,∴a+b+c<0,故B错误;
由图象可知当x=-1时,y>0,∴a-b+c>0,∴b∵b=-2a,∴a=-,∴--b+c>0,∴c>,∴2c>3b,故C正确.故选AC.
35.答案 -1解析 抛物线的对称轴为直线x=-=1,
∵a>0,∴抛物线开口向上.
①若点A在对称轴直线x=1的左侧,点B在对称轴直线x=1的右侧,
则不等式组无解;
②若点B在对称轴直线x=1的左侧,点A在对称轴直线x=1的右侧,则
解得-136.答案
解析 解得
∴A(1,2),B(4,5).
如图,作点A关于y轴对称的点A',连接A'B交y轴于点P,此时△PAB的周长最小,则A'(-1,2).
设直线A'B的解析式为y=kx+b(k≠0),把A'(-1,2),B(4,5)代入,
得解得
∴直线A'B的解析式为y=x+.
当x=0时,y=,
∴当△PAB的周长最小时,点P的坐标为.
设直线AB与y轴交于点C,则C(0,1),
∴S△PAB=S△PCB-S△PCA=××4-××1=.
方法解读 本题属于将军饮马模型,要使△PAB的周长最小,需作点A关于y轴的对称点A',连接A'B交y轴于点P,此时△PAB的周长最小,求出点P的坐标即可求出面积.
素养探究全练
37.解析 (1)y=4-(6-x)2=-(x-6)2+4,
∴抛物线对称轴为直线x=6,∵-1<0,
∴抛物线开口向下,y有最大值,y的最大值为4.
把P(a,3)代入y=4-(6-x)2中,得4-(6-a)2=3,
解得a=5或a=7,
∵点P(a,3)在C的对称轴右侧,∴a=7.
(2)y=-x2+6x-9=-(x-3)2,
抛物线y=-(x-3)2是由抛物线y=-(x-6)2+4向左平移3个单位长度,再向下平移4个单位长度得到的,∴平移的距离为=5,
∴点P'移动的最短路程为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第5章 对函数的再探索
5.4 二次函数的图象和性质
第3课时 二次函数y=a(x-h)2+k和y=ax2+bx+c的图象和性质
基础过关全练
知识点4 二次函数y=a(x-h)2+k的图象和性质及图象的平移规律
18.(2023甘肃兰州中考)已知二次函数y=-3(x-2)2-3,下列说法正确的是( )
A.图象的对称轴为直线x=-2 B.图象的顶点坐标为(2,3)
C.函数的最大值是-3 D.函数的最小值是-3
19.(2023江苏徐州中考)在平面直角坐标系中,将二次函数y=(x+1)2+3的图象向右平移2个单位长度,再向下平移1个单位长度,所得抛物线对应的函数表达式为 ( )
A.y=(x+3)2+2 B.y=(x-1)2+2
C.y=(x-1)2+4 D.y=(x+3)2+4
20.(2020江苏南京中考)下列关于二次函数y=-(x-m)2+m2+1(m为常数)的结论:①该函数的图象与函数y=-x2的图象形状相同;②该函数的图象一定经过点(0,1);③当x>0时,y随x的增大而减小;④该函数的图象的顶点在函数y=x2+1的图象上.其中所有正确结论的序号是 .
知识点5 二次函数y=ax2+bx+c的图象和性质
21.(2022山东淄博临淄期末)二次函数y=-x2-(k-4)x+6中,当x>-2时,y随着x的增大而减小,当x<-2时,y随着x的增大而增大,则k的值为 ( )
A.-8 B.-4 C.4 D.8
22.(2023山东青州期末)对于二次函数y=x2+4x+5的图象,下列说法不正确的是( )
A.开口向上 B.对称轴是直线x=2
C.顶点坐标是(-2,1) D.与x轴没有交点
23.【新考法】(2022山东菏泽牡丹一模)老师设计了接力游戏,用合作的方式完成“求抛物线y=2x2+4x-4的顶点坐标”,规则如下:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成解答.过程如图所示:
接力中,自己负责的一步出现错误的是 ( )
A.只有丁 B.乙和丁 C.乙和丙 D.甲和丁
知识点6 二次函数y=ax2+bx+c的图象特征与a,b,c的符号之间的关系
24.(2023山东东明一模)在同一平面直角坐标系中,二次函数y=ax2与一次函数y=bx+c的图象如图所示,则二次函数y=ax2+bx+c的图象可能是 ( )
A. B. C. D.
能力提升全练
25.(2023四川南充中考,7,★★☆)若点P(m,n)在抛物线y=ax2(a≠0)上,则下列各点在抛物线y=a(x+1)2上的是 ( )
A.(m,n+1) B.(m+1,n) C.(m,n-1) D.(m-1,n)
26.【新考法】(2023广东中考,10,★★☆)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为 ( )
A.-1 B.-2 C.-3 D.-4
27.(2022浙江宁波中考,9,★★☆)点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上.若y1
①向右平移2个单位长度;
②向右平移1个单位长度,再向下平移1个单位长度;
③向下平移4个单位长度;
④沿x轴翻折,再向上平移4个单位长度.
你认为小嘉说的方法中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
29.(2023江苏扬州中考,8,★★☆)已知二次函数y=ax2-2x+(a为常数,且a>0),下列结论:①函数图象一定经过第一、二、四象限;②函数图象一定不经过第三象限;③当x<0时,y随x的增大而减小;④当x>0时,y随x的增大而增大.其中所有正确结论的序号是 ( )
A.①② B.②③ C.② D.③④
30.(2023浙江台州中考,10,★★☆)抛物线y=ax2-a(a≠0)与直线y=kx交于A(x1,y1),B(x2,y2)两点,若x1+x2<0,则直线y=ax+k一定经过 ( )
A.第一、二象限 B.第二、三象限
C.第三、四象限 D.第一、四象限
31.【排除法】(2022湖南株洲中考,10,★★☆)已知二次函数y=ax2+bx-c(a≠0),其中b>0,c>0,则该函数的图象可能为( )
A. B.
C. D.
32.(2023山东济南莱芜二模,10,★★☆)在平面直角坐标系中,若点M(x1,y1),N(x2,y2)(x1
A.0
34.【山东潍坊常考·多选题】(2023山东潍坊三模,9,★★☆)(多选题)如图,抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,则下列结论正确的是 ( )
A.abc>0 B.a+b+c>0 C.3b<2c D.b>a+c
35.(2023福建中考,16,★★☆)已知抛物线y=ax2-2ax+b(a>0)经过A(2n+3,y1),B(n-1,y2)两点,若A,B分别位于抛物线对称轴的两侧,且y1
素养探究全练
37.【模型观念】(2022河北中考)如图,点P(a,3)在抛物线C:y=4-(6-x)2上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上画出点P及C的一段,分别记为P',C'.平移该胶片,使C'所在抛物线对应的函数解析式恰为y=-x2+6x-9.求点P'移动的最短路程.
答案全解全析
基础过关全练
18.C 二次函数y=-3(x-2)2-3的图象的开口向下,对称轴为直线x=2,顶点坐标为(2,-3),当x=2时,y有最大值,为-3,故选C.
19.B 将二次函数y=(x+1)2+3的图象向右平移2个单位长度,再向下平移1个单位长度,所得抛物线对应的函数表达式为y=(x+1-2)2+3-1,即y=(x-1)2+2.故选B.
20.答案 ①②④
解析 ∵二次函数y=-(x-m)2+m2+1(m为常数)与函数y=-x2的二次项系数都为-1,∴两函数图象的形状相同,故结论①正确;在函数y=-(x-m)2+m2+1中,令x=0,得y=-m2+m2+1=1,∴该函数的图象一定经过点(0,1),故结论②正确;由解析式可得抛物线开口向下,对称轴为直线x=m,当x>m时,y随x的增大而减小,故结论③错误;∵抛物线开口向下,∴当x=m时,函数y有最大值,为m2+1,∴该函数图象的顶点在函数y=x2+1的图象上,故结论④正确.综上,正确的结论为①②④.
21.D 由题意可知,抛物线对称轴为直线x=-2,
∴-=-2,解得k=8.
22.B ∵y=x2+4x+5=(x+2)2+1,∴抛物线开口向上,对称轴是直线x=-2,顶点坐标是(-2,1),故A,C选项正确,B选项错误,∵顶点在第二象限,抛物线开口向上,∴抛物线与x轴没有交点,故D选项正确.故选B.
23.D 本题通过接力游戏的方式让学生学会将二次函数的一般式化为顶点式,题目中同时呈现了错例,增强学习效果.甲的运算应为y=2x2+4x-4=2(x2+2x-2);乙和丙的运算正确;由丙的结果可知顶点坐标为(1,-3),所以出现错误的是甲和丁.故选D.
24.D 观察函数图象可知,a>0,b>0,c<0,∴-<0,∴二次函数y=ax2+bx+c的图象开口向上,对称轴在y轴左侧,与y轴的交点在y轴负半轴上.故选D.
能力提升全练
25.D ∵点P(m,n)在抛物线y=ax2(a≠0)上,
∴n=am2,∴二次函数y=a(x+1)2(a≠0)中,当x+1=m时,y=n,此时x=m-1,即当x=m-1时,y=n,
∴点(m-1,n)在抛物线y=a(x+1)2上,故选D.
26.B 本题结合正方形的性质考查字母系数之间的关系.
如图,连接AC,交OB于点E,
∵四边形OABC是正方形,∴OE=AE=OB.
由题意可知B(0,c),∴A.
将A点坐标代入y=ax2+c得=a·+c.
化简得ac2=-2c.∵c≠0,∴ac=-2,故选B.
27.B ∵点A(m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上,
∴y1=(m-1-1)2+n=(m-2)2+n,y2=(m-1)2+n,
∵y1
∴m>,故选B.
28.D 此类题目一般考查平移后函数的图象,本题考查通过四种不同的平移方法看图象是否经过点(2,0).①将二次函数y=x2的图象向右平移2个单位长度得到y=(x-2)2的图象,当x=2时,y=(2-2)2=0,故①正确;
②将二次函数y=x2的图象向右平移1个单位长度,再向下平移1个单位长度得到y=(x-1)2-1的图象,当x=2时,y=(2-1)2-1=0,故②正确;
③将二次函数y=x2的图象向下平移4个单位长度得到y=x2-4的图象,当x=2时,y=22-4=0,故③正确;
④将二次函数y=x2的图象沿x轴翻折,再向上平移4个单位长度得到y=-x2+4的图象,当x=2时,y=-22+4=0,故④正确.
综上所述,正确的个数为4.故选D.
29.B ∵a>0,b=-2<0,c=>0,
∴抛物线开口向上,对称轴在y轴右侧,与y轴的交点在y轴正半轴上.
∴图象一定经过第一、二象限,一定不经过第三象限,可能经过第四象限,故①错误,②正确.
∵抛物线开口向上,对称轴在y轴右侧,
∴当x<0时,y随x的增大而减小,故③正确;当x>0时,图象先下降后上升,故④错误.综上,正确结论的序号是②③,故选B.
30.D ∵抛物线y=ax2-a(a≠0)与直线y=kx交于A(x1,y1),B(x2,y2)两点,∴kx=ax2-a,
∴ax2-kx-a=0,∴x1+x2=,∵x1+x2<0,
∴<0,∴a,k异号.
①当a>0,k<0时,直线y=ax+k经过第一、三、四象限,
②当a<0,k>0时,直线y=ax+k经过第一、二、四象限,
综上,直线y=ax+k一定经过第一、四象限.故选D.
31.C 对于二次函数y=ax2+bx-c(a≠0),
令x=0,则y=-c,
∴抛物线与y轴的交点坐标为(0,-c),
∵c>0,∴-c<0,
∴抛物线与y轴的交点在y轴的负半轴上,
可以排除A选项和D选项;
B选项和C选项中,抛物线的对称轴为直线x=->0,∵b>0,∴a<0,
∴抛物线开口向下,可以排除B选项.故选C.
方法解读 本题需用排除法找出符合条件的函数图象,先根据c的符号确定抛物线与y轴的交点可排除两个选项,再根据对称轴的位置排除一个错误选项,剩余的即为可能的函数图象.
32.A 由y1>y2可得,(m-2x1+m)-(m-2x2+m)>0,
整理,得(x1-x2)[m(x1+x2)-2]>0,
∵x1+x2=4,∴(x1-x2)(4m-2)>0,
∵x1
∴二次函数y=-x2-2x+3的图象向右平移k(k>0)个单位得到y1=-(x+1-k)2+4的图象,
∴函数y1的图象的对称轴为直线x=k-1,
∵当-1
故A、B选项符合题意,故选AB.
34.AC 由图象得a>0,c<0,-=1,∴b=-2a<0,
∴abc>0,故A正确;
由图象可知,当x=1时,y<0,∴a+b+c<0,故B错误;
由图象可知当x=-1时,y>0,∴a-b+c>0,∴b
35.答案 -1
∵a>0,∴抛物线开口向上.
①若点A在对称轴直线x=1的左侧,点B在对称轴直线x=1的右侧,
则不等式组无解;
②若点B在对称轴直线x=1的左侧,点A在对称轴直线x=1的右侧,则
解得-1
解析 解得
∴A(1,2),B(4,5).
如图,作点A关于y轴对称的点A',连接A'B交y轴于点P,此时△PAB的周长最小,则A'(-1,2).
设直线A'B的解析式为y=kx+b(k≠0),把A'(-1,2),B(4,5)代入,
得解得
∴直线A'B的解析式为y=x+.
当x=0时,y=,
∴当△PAB的周长最小时,点P的坐标为.
设直线AB与y轴交于点C,则C(0,1),
∴S△PAB=S△PCB-S△PCA=××4-××1=.
方法解读 本题属于将军饮马模型,要使△PAB的周长最小,需作点A关于y轴的对称点A',连接A'B交y轴于点P,此时△PAB的周长最小,求出点P的坐标即可求出面积.
素养探究全练
37.解析 (1)y=4-(6-x)2=-(x-6)2+4,
∴抛物线对称轴为直线x=6,∵-1<0,
∴抛物线开口向下,y有最大值,y的最大值为4.
把P(a,3)代入y=4-(6-x)2中,得4-(6-a)2=3,
解得a=5或a=7,
∵点P(a,3)在C的对称轴右侧,∴a=7.
(2)y=-x2+6x-9=-(x-3)2,
抛物线y=-(x-3)2是由抛物线y=-(x-6)2+4向左平移3个单位长度,再向下平移4个单位长度得到的,∴平移的距离为=5,
∴点P'移动的最短路程为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
