7.2 直棱柱的侧面展开图课时练(含解析)
文档属性
| 名称 | 7.2 直棱柱的侧面展开图课时练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 430.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 20:55:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第7章 空间图形的初步认识
7.2 直棱柱的侧面展开图
基础过关全练
知识点 直棱柱的概念、直棱柱的侧面展开图及其面积
1.(2023山东莱阳期末)若一个棱柱有7个面,则它是 ( )
A.七棱柱 B.六棱柱 C.五棱柱 D.四棱柱
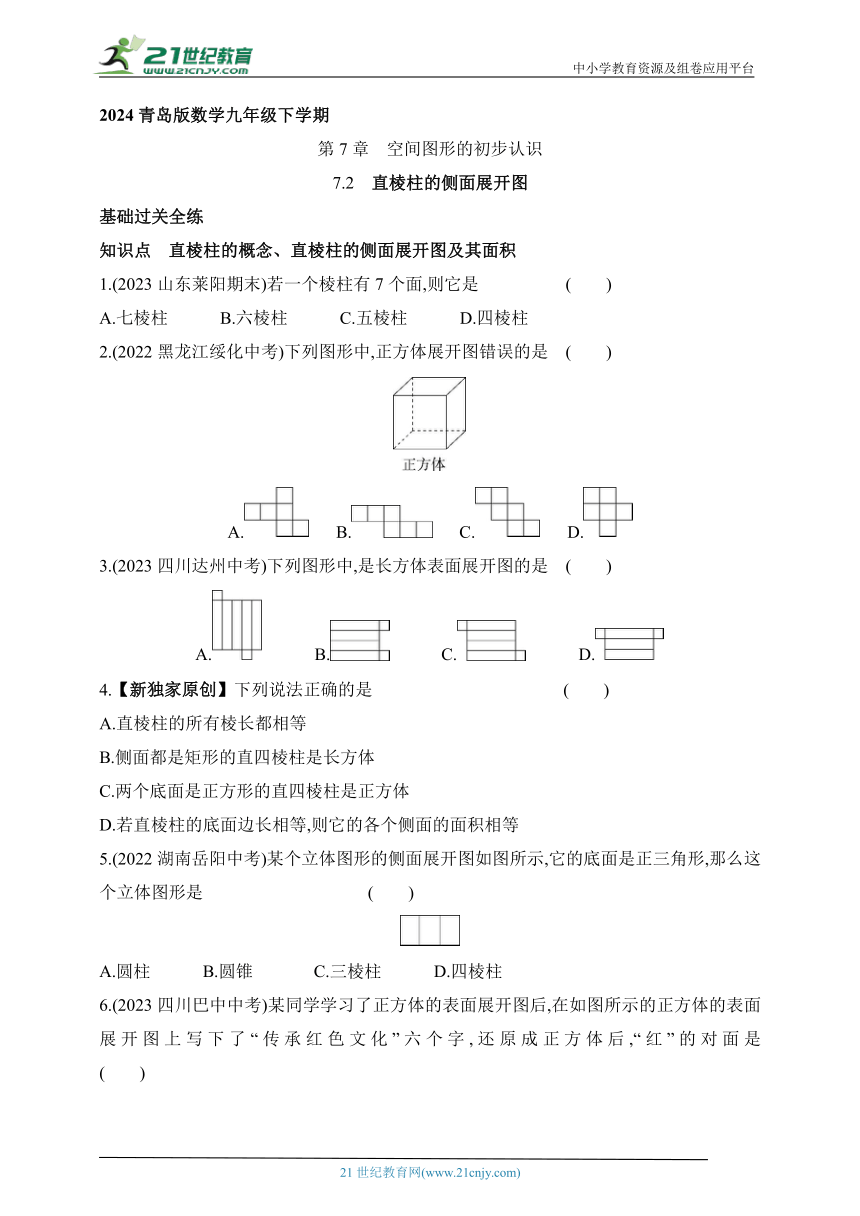
2.(2022黑龙江绥化中考)下列图形中,正方体展开图错误的是 ( )
A. B. C. D.
3.(2023四川达州中考)下列图形中,是长方体表面展开图的是 ( )
A. B. C. D.
4.【新独家原创】下列说法正确的是 ( )
A.直棱柱的所有棱长都相等
B.侧面都是矩形的直四棱柱是长方体
C.两个底面是正方形的直四棱柱是正方体
D.若直棱柱的底面边长相等,则它的各个侧面的面积相等
5.(2022湖南岳阳中考)某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是 ( )
A.圆柱 B.圆锥 C.三棱柱 D.四棱柱
6.(2023四川巴中中考)某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是 ( )
A.传 B.承 C.文 D.化
7.(2022山东莘县期中)从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
8.如图所示的是一个底面是直角三角形的直三棱柱和它的侧面展开图,其中线段AB=EF=MN=CD=8 cm,若AC=12 cm,底面三角形的斜边AE=5 cm,求这个直三棱柱的表面积.
能力提升全练
9.【规律探究题】(2023山东临朐期末,8,★★☆)有一个正方体骰子放在桌面上,将骰子按如图所示的方式顺时针滚动,每滚动90°算一次,则滚动第2 022次后,骰子朝下一面的点数是 ( )
A.5 B.3 C.4 D.2
10.【实践探究题】(2023山东单县期中,9,★★☆)如图,有10个无阴影的小正方形,现从中选取1个,使它与图中阴影部分能折叠成封闭的一个正方体的纸盒,则选取的方法一共有 ( )
A.2种 B.3种 C.4种 D.5种
11.【最短距离问题】(2023山东鄄城期中,7,★★☆)如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,则它所爬行的最短路线的长是 ( )
A.10 B.14 C. D.8
12.【新考法】(2022江苏南京中考,6,★★☆)直三棱柱的表面展开图如图所示,AC=3,BC=4,AB=5,四边形AMNB是正方形,将其折叠成直三棱柱后,下列各点中,与点C距离最大的是 ( )
A.点M B.点N C.点P D.点Q
13.(2022山东泰安肥城期末,25,★★☆)小明在学习了“展开与折叠”这一节后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个长方体纸盒如图1,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图2中的a和b.根据你所学的知识,回答下列问题:
(1)小明共剪了 刀;
(2)现在小明想将图2中剪断的b重新粘贴到a上,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到a中的什么位置 请你帮助小明在a上补全;
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
素养探究全练
14.【空间观念】如图,一个长方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长;
(3)在(2)的条件下,求点B1到最短路径的距离.
答案全解全析
基础过关全练
1.C ∵棱柱有2个底面,共有7个面,
∴侧面个数为7-2=5,
∴它是五棱柱,故选C.
2.D 由正方体的11种展开图可知,含“田”字形的一定不是正方体的展开图,故D选项错误,符合题意.故选D.
3.C 长方体的侧面有4个,故可排除选项A、D,B选项两个底面在同侧,不是长方体的表面展开图,只有C选项符合题意,故选C.
4.D A.直棱柱的侧棱长都相等,但与上、下底面的两个多边形的边的长不一定相等,故A说法错误;B.底面是任意四边形的直棱柱侧面都是矩形,不一定是长方体,故B说法错误;C.两个底面是正方形,如果侧棱长与底面正方形的边长不相等,则不是正方体,故C说法错误;D.因为直棱柱的底面的边的长相等,侧棱长相等,每个侧面的面积=底面边的长×侧棱长,所以每个侧面的面积相等,故D说法正确.故选D.
5.C 由题意可知,该立体图形的上、下底面是正三角形,侧面是三个全等的矩形,所以这个立体图形是三棱柱,故选C.
6.D 将题图中的表面展开图还原成正方体后可知,“传”与“文”相对,“承”与“色”相对,“红”与“化”相对.故选D.
7.答案 24
解析 挖去一个棱长为1的小正方体,得到的图形与原图形的表面积相等,则所求表面积是2×2×6=24.
8.解析 ∵AC=12 cm,AE=5 cm,∴CE=12-5=7 cm,
设EM=x cm,则MC=(7-x)cm,
根据勾股定理可得x2+(7-x)2=52,
解得x1=3,x2=4,
∴直角三角形的两直角边长分别为3 cm和4 cm.
∴S底=×3×4=6 cm2.
又∵S侧=12×8=96 cm2,∴S表=96+6×2=108 cm2.
故这个直三棱柱的表面积为108 cm2.
能力提升全练
9.B 根据翻转规律,从第1次开始,骰子朝下一面的点数以2,3,5,4为一组依次循环,∵2 022÷4=505……2,∴滚动第2 022次后,骰子朝下一面的点数是3.故选B.
10.C 如图所示,共4种.
11.A 将长方体的两个面展开,分两种情况,
第一种展开方式如图①,∴AB==10,
第二种展开方式如图②,∴AB==,
∵10<,∴一只蚂蚁从A点沿纸箱爬到B点,所爬行的最短路线的长是10,故选A.
方法解读 求立体图形表面上两点间的最短距离,一般需将有关的侧面展开,变为平面图形,然后利用勾股定理进行解答,本题是长方体,需分类讨论.
12.B 此类题目一般考查把立体图形展开求最短距离,本题要求由展开图折叠成立体图形求最大距离.
∵AC=3,BC=4,AB=5,32+42=52,
∴△ACB是直角三角形,
∵四边形AMNB是正方形,立方体是直三棱柱,
∴直三棱柱的高AM=AB=5.
∴折叠成直三棱柱后,CP=CM==,
CN==,CQ=AM=5.
∵>>5,
∴与点C距离最大的是点N,故选B.
13.解析 (1)小明共剪了8刀.故答案为8.
(2)如图,有以下四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱即高为a cm,则长与宽均为5a cm.
∵长方体纸盒所有棱长的和是880 cm,
∴4(a+5a+5a)=880,解得a=20,
则长和宽均为100 cm,
∴这个长方体纸盒的体积为20×100×100=200 000(cm3).
素养探究全练
14.解析 (1)如图,在矩形ABC'1D1或矩形ACC1A1中蚂蚁能够最快到达目的地的可能路径为AC'1或AC1.
(2)AC'1==,
AC1==.
∵AC'1>AC1,∴蚂蚁爬过的最短路径的长是.
(3)由(2)可知,AC1是最短路径,如图,作B1E⊥AC1于E,
∵∠C1A1A=∠C1EB1,∠A1C1A=∠EC1B1,
∴△AA1C1∽△B1EC1,
∴=,即=,∴B1E=.
故点B1到最短路径的距离为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第7章 空间图形的初步认识
7.2 直棱柱的侧面展开图
基础过关全练
知识点 直棱柱的概念、直棱柱的侧面展开图及其面积
1.(2023山东莱阳期末)若一个棱柱有7个面,则它是 ( )
A.七棱柱 B.六棱柱 C.五棱柱 D.四棱柱
2.(2022黑龙江绥化中考)下列图形中,正方体展开图错误的是 ( )
A. B. C. D.
3.(2023四川达州中考)下列图形中,是长方体表面展开图的是 ( )
A. B. C. D.
4.【新独家原创】下列说法正确的是 ( )
A.直棱柱的所有棱长都相等
B.侧面都是矩形的直四棱柱是长方体
C.两个底面是正方形的直四棱柱是正方体
D.若直棱柱的底面边长相等,则它的各个侧面的面积相等
5.(2022湖南岳阳中考)某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是 ( )
A.圆柱 B.圆锥 C.三棱柱 D.四棱柱
6.(2023四川巴中中考)某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是 ( )
A.传 B.承 C.文 D.化
7.(2022山东莘县期中)从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
8.如图所示的是一个底面是直角三角形的直三棱柱和它的侧面展开图,其中线段AB=EF=MN=CD=8 cm,若AC=12 cm,底面三角形的斜边AE=5 cm,求这个直三棱柱的表面积.
能力提升全练
9.【规律探究题】(2023山东临朐期末,8,★★☆)有一个正方体骰子放在桌面上,将骰子按如图所示的方式顺时针滚动,每滚动90°算一次,则滚动第2 022次后,骰子朝下一面的点数是 ( )
A.5 B.3 C.4 D.2
10.【实践探究题】(2023山东单县期中,9,★★☆)如图,有10个无阴影的小正方形,现从中选取1个,使它与图中阴影部分能折叠成封闭的一个正方体的纸盒,则选取的方法一共有 ( )
A.2种 B.3种 C.4种 D.5种
11.【最短距离问题】(2023山东鄄城期中,7,★★☆)如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,则它所爬行的最短路线的长是 ( )
A.10 B.14 C. D.8
12.【新考法】(2022江苏南京中考,6,★★☆)直三棱柱的表面展开图如图所示,AC=3,BC=4,AB=5,四边形AMNB是正方形,将其折叠成直三棱柱后,下列各点中,与点C距离最大的是 ( )
A.点M B.点N C.点P D.点Q
13.(2022山东泰安肥城期末,25,★★☆)小明在学习了“展开与折叠”这一节后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个长方体纸盒如图1,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图2中的a和b.根据你所学的知识,回答下列问题:
(1)小明共剪了 刀;
(2)现在小明想将图2中剪断的b重新粘贴到a上,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到a中的什么位置 请你帮助小明在a上补全;
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880 cm,求这个长方体纸盒的体积.
素养探究全练
14.【空间观念】如图,一个长方体木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长;
(3)在(2)的条件下,求点B1到最短路径的距离.
答案全解全析
基础过关全练
1.C ∵棱柱有2个底面,共有7个面,
∴侧面个数为7-2=5,
∴它是五棱柱,故选C.
2.D 由正方体的11种展开图可知,含“田”字形的一定不是正方体的展开图,故D选项错误,符合题意.故选D.
3.C 长方体的侧面有4个,故可排除选项A、D,B选项两个底面在同侧,不是长方体的表面展开图,只有C选项符合题意,故选C.
4.D A.直棱柱的侧棱长都相等,但与上、下底面的两个多边形的边的长不一定相等,故A说法错误;B.底面是任意四边形的直棱柱侧面都是矩形,不一定是长方体,故B说法错误;C.两个底面是正方形,如果侧棱长与底面正方形的边长不相等,则不是正方体,故C说法错误;D.因为直棱柱的底面的边的长相等,侧棱长相等,每个侧面的面积=底面边的长×侧棱长,所以每个侧面的面积相等,故D说法正确.故选D.
5.C 由题意可知,该立体图形的上、下底面是正三角形,侧面是三个全等的矩形,所以这个立体图形是三棱柱,故选C.
6.D 将题图中的表面展开图还原成正方体后可知,“传”与“文”相对,“承”与“色”相对,“红”与“化”相对.故选D.
7.答案 24
解析 挖去一个棱长为1的小正方体,得到的图形与原图形的表面积相等,则所求表面积是2×2×6=24.
8.解析 ∵AC=12 cm,AE=5 cm,∴CE=12-5=7 cm,
设EM=x cm,则MC=(7-x)cm,
根据勾股定理可得x2+(7-x)2=52,
解得x1=3,x2=4,
∴直角三角形的两直角边长分别为3 cm和4 cm.
∴S底=×3×4=6 cm2.
又∵S侧=12×8=96 cm2,∴S表=96+6×2=108 cm2.
故这个直三棱柱的表面积为108 cm2.
能力提升全练
9.B 根据翻转规律,从第1次开始,骰子朝下一面的点数以2,3,5,4为一组依次循环,∵2 022÷4=505……2,∴滚动第2 022次后,骰子朝下一面的点数是3.故选B.
10.C 如图所示,共4种.
11.A 将长方体的两个面展开,分两种情况,
第一种展开方式如图①,∴AB==10,
第二种展开方式如图②,∴AB==,
∵10<,∴一只蚂蚁从A点沿纸箱爬到B点,所爬行的最短路线的长是10,故选A.
方法解读 求立体图形表面上两点间的最短距离,一般需将有关的侧面展开,变为平面图形,然后利用勾股定理进行解答,本题是长方体,需分类讨论.
12.B 此类题目一般考查把立体图形展开求最短距离,本题要求由展开图折叠成立体图形求最大距离.
∵AC=3,BC=4,AB=5,32+42=52,
∴△ACB是直角三角形,
∵四边形AMNB是正方形,立方体是直三棱柱,
∴直三棱柱的高AM=AB=5.
∴折叠成直三棱柱后,CP=CM==,
CN==,CQ=AM=5.
∵>>5,
∴与点C距离最大的是点N,故选B.
13.解析 (1)小明共剪了8刀.故答案为8.
(2)如图,有以下四种情况.
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱即高为a cm,则长与宽均为5a cm.
∵长方体纸盒所有棱长的和是880 cm,
∴4(a+5a+5a)=880,解得a=20,
则长和宽均为100 cm,
∴这个长方体纸盒的体积为20×100×100=200 000(cm3).
素养探究全练
14.解析 (1)如图,在矩形ABC'1D1或矩形ACC1A1中蚂蚁能够最快到达目的地的可能路径为AC'1或AC1.
(2)AC'1==,
AC1==.
∵AC'1>AC1,∴蚂蚁爬过的最短路径的长是.
(3)由(2)可知,AC1是最短路径,如图,作B1E⊥AC1于E,
∵∠C1A1A=∠C1EB1,∠A1C1A=∠EC1B1,
∴△AA1C1∽△B1EC1,
∴=,即=,∴B1E=.
故点B1到最短路径的距离为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
