7.3 圆柱的侧面展开图课时练(含解析)
文档属性
| 名称 | 7.3 圆柱的侧面展开图课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 393.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 20:56:26 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第7章 空间图形的初步认识
7.3 圆柱的侧面展开图
基础过关全练
知识点 圆柱的形成及侧面展开图
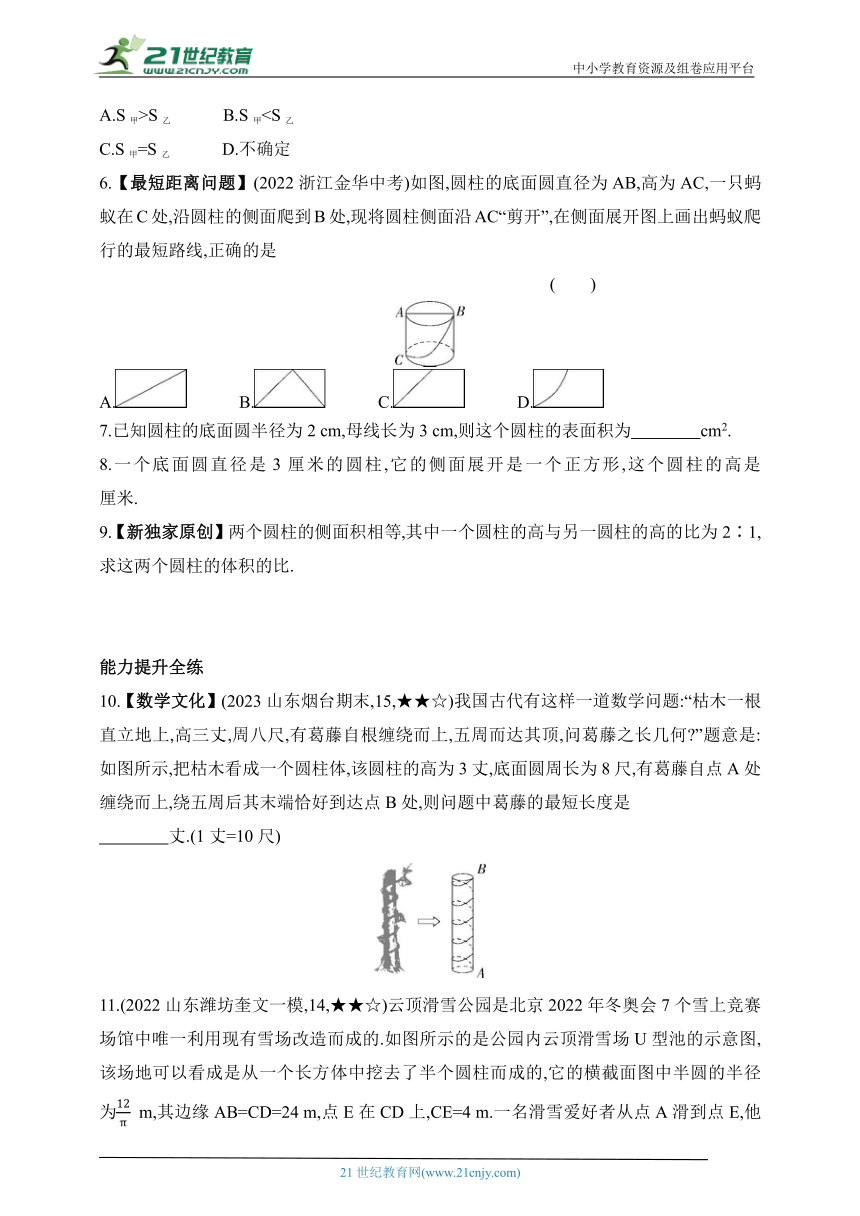
1.(2022江苏常州中考)下列图形中,为圆柱的侧面展开图的是 ( )
A. B. C. D.
2.(2023江苏宿迁一模)若圆柱的底面圆半径为3 cm,母线长为4 cm,则这个圆柱的侧面积为 ( )
A.12 cm2 B.24 cm2
C.12π cm2 D.24π cm2
3.(2023黑龙江肇源期中)一个圆柱的底面圆半径扩大为原来的2倍,高缩小到原来的,它的侧面积 ( )
A.扩大为原来的2倍 B.缩小到原来的
C.不变 D.扩大为原来的4倍
4.如图,圆柱的母线长为10 cm,轴截面的面积为240 cm2,则圆柱的侧面积是 ( )
A.240 cm2 B.240π cm2
C.480 cm2 D.480π cm2
5.【教材变式·P148T3】(2022北京东城期末)如图所示,在长方形ABCD中,AB=a,BC=b,且a>b,将长方形ABCD绕边AB所在的直线旋转一周形成圆柱甲,将长方形ABCD绕边BC所在直线旋转一周形成圆柱乙,记两个圆柱的侧面积分别为S甲、S乙,则结论中正确的是 ( )
A.S甲>S乙 B.S甲C.S甲=S乙 D.不确定
6.【最短距离问题】(2022浙江金华中考)如图,圆柱的底面圆直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最短路线,正确的是
( )
A. B. C. D.
7.已知圆柱的底面圆半径为2 cm,母线长为3 cm,则这个圆柱的表面积为 cm2.
8.一个底面圆直径是3厘米的圆柱,它的侧面展开是一个正方形,这个圆柱的高是 厘米.
9.【新独家原创】两个圆柱的侧面积相等,其中一个圆柱的高与另一圆柱的高的比为2∶1,求这两个圆柱的体积的比.
能力提升全练
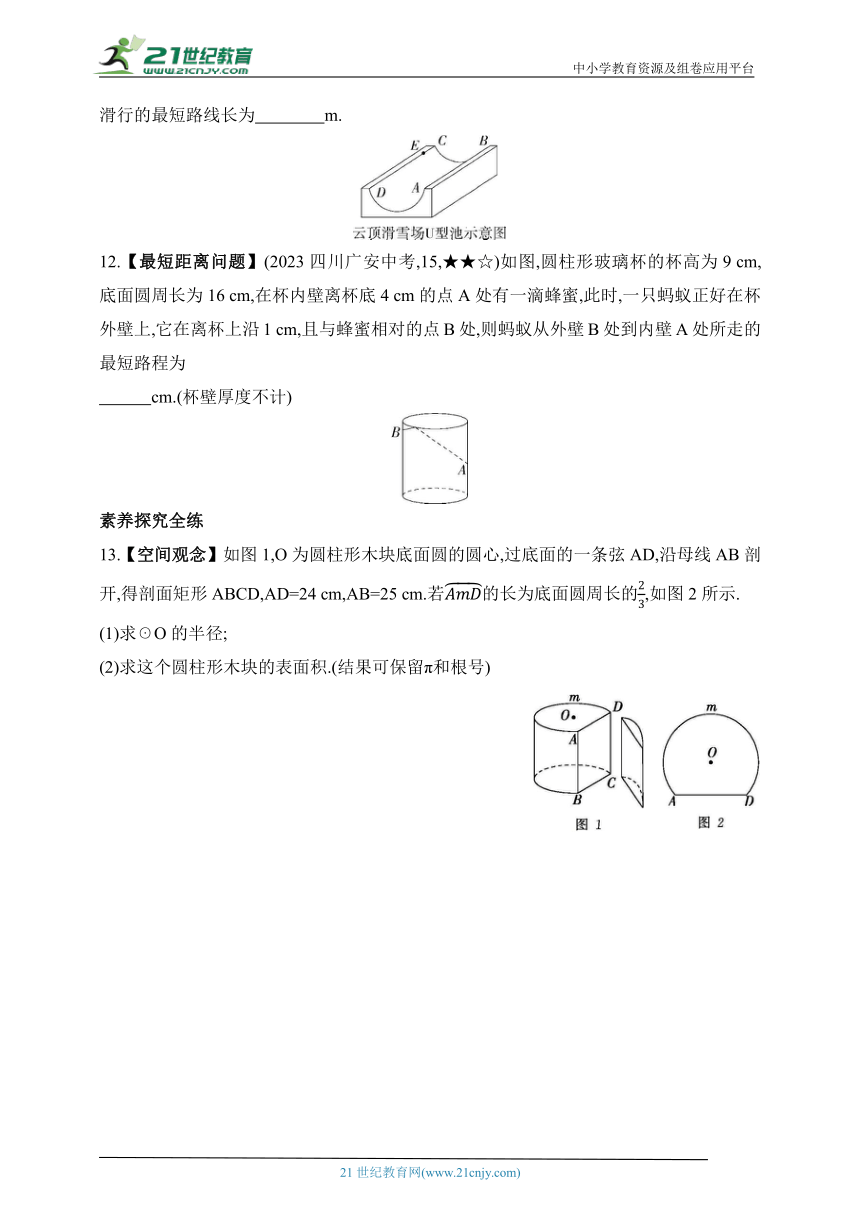
10.【数学文化】(2023山东烟台期末,15,★★☆)我国古代有这样一道数学问题:“枯木一根直立地上,高三丈,周八尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何 ”题意是:如图所示,把枯木看成一个圆柱体,该圆柱的高为3丈,底面圆周长为8尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是
丈.(1丈=10尺)
11.(2022山东潍坊奎文一模,14,★★☆)云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的.如图所示的是公园内云顶滑雪场U型池的示意图,该场地可以看成是从一个长方体中挖去了半个圆柱而成的,它的横截面图中半圆的半径为 m,其边缘AB=CD=24 m,点E在CD上,CE=4 m.一名滑雪爱好者从点A滑到点E,他滑行的最短路线长为 m.
12.【最短距离问题】(2023四川广安中考,15,★★☆)如图,圆柱形玻璃杯的杯高为9 cm,底面圆周长为16 cm,在杯内壁离杯底4 cm的点A处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿1 cm,且与蜂蜜相对的点B处,则蚂蚁从外壁B处到内壁A处所走的最短路程为
cm.(杯壁厚度不计)
素养探究全练
13.【空间观念】如图1,O为圆柱形木块底面圆的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24 cm,AB=25 cm.若的长为底面圆周长的,如图2所示.
(1)求☉O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留π和根号)
答案全解全析
基础过关全练
1.D 圆柱的侧面展开图是矩形,故选D.
2.D 根据侧面积公式可得,S侧=2π×3×4=24π cm2,故选D.
3.C 设原来圆柱的底面圆半径为r,高为h,则原来的侧面积为2πrh,
底面圆半径扩大为原来的2倍后变为2r,高缩小到原来的变为h,
∴变化后的侧面积为2π·2r·h=2πrh,∴侧面积不变.故选C.
4.B ∵圆柱的母线长为10 cm,轴截面的面积为240 cm2,∴圆柱的底面圆直径是240÷10=24 cm,所以S侧=24π×10=240π cm2.故选B.
5.C ∵S甲=2π×b×a=2πab,S乙=2π×a×b=2πab,
∴S甲=S乙.故选C.
6.C 将圆柱侧面沿AC“剪开”,侧面展开图为矩形,∵圆柱的底面圆直径为AB,∴蚂蚁爬行的最短路线是C中的路线.
7.答案 20π
解析 S底=π×22=4π cm2,S侧=2π×2×3=12π cm2,
∴S表=2×4π+12π=8π+12π=20π cm2.
8.答案 3π
解析 ∵圆柱的底面圆直径是3厘米,
∴底面圆周长为π×3=3π厘米,
∵它的侧面展开是一个正方形,
∴圆柱的高是3π厘米.
9.解析 设两个圆柱的侧面积分别为S1,S2,底面圆半径分别为r1,r2,高分别为h1,h2(h1>h2),体积分别为V1,V2.则S1=2πr1h1,S2=2πr2h2.
∵侧面积相等,高的比为2∶1,
∴S1=S2,h1=2h2.
∴2πr1h1=2πr2h2.
∴r2=2r1.
∴===.
即这两个圆柱的体积的比为1∶2.
能力提升全练
10.答案 5
解析 如图所示,线段AB的长即为葛藤的最短长度,
∵8尺=0.8丈,
∴AC=0.8×5=4丈,
在Rt△ABC中,
AB===5丈.
11.答案 4
解析 如图,线段AE的长度即为他滑行的最短路线长.
根据题意可知AD=2π××=12(m),DE=CD-CE=24-4=20(m),
在Rt△ADE中,根据勾股定理,得
AE===4(m).
故他滑行的最短路线长为4 m.
12.答案 10
解析 如图,将杯子侧面展开,分别标注字母C、D、E、F,作点B关于CF的对称点B',连接AB'交CF于点P,连接BP,此时BP+AP的值最小,为AB'的长,即AB'为最短路径.
过点A作AG⊥CD,垂足为G,
由题意可得,AG=×16=8 cm,DG=AE=4 cm,
∵B'C=BC=1 cm,∴B'G=9-4+1=6 cm,
在Rt△AB'G中,AB'===10 cm.
∴蚂蚁从外壁B处到内壁A处所走的最短路程为10 cm.
方法解读 本题考查立体图形侧面上两点间的最短距离,但由于蜂蜜与蚂蚁的位置分别在杯子内外,故应先将圆柱的侧面展开,然后作点B(或点A)关于杯口展开直线的对称点,利用“将军饮马”模型结合勾股定理进行解答.
素养探究全练
13.解析 (1)如图,连接OA,OD,过O作OE⊥AD,垂足为E,
∵的长为底面圆周长的,
∴的度数为360°×=240°,
∴∠AOD=360°-240°=120°.
∵OE⊥AD,OA=OD,
∴∠AOE=×120°=60°,AE=AD=12 cm.
在Rt△AOE中,sin∠AOE=,即sin 60°=,
∴AO=8 cm,即☉O的半径为8 cm.
(2)设圆柱的表面积为S cm2,
则S=2S底+S侧=2π×+2π×8×25=384π+400π.
答:这个圆柱形木块的表面积为(384π+400π)cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第7章 空间图形的初步认识
7.3 圆柱的侧面展开图
基础过关全练
知识点 圆柱的形成及侧面展开图
1.(2022江苏常州中考)下列图形中,为圆柱的侧面展开图的是 ( )
A. B. C. D.
2.(2023江苏宿迁一模)若圆柱的底面圆半径为3 cm,母线长为4 cm,则这个圆柱的侧面积为 ( )
A.12 cm2 B.24 cm2
C.12π cm2 D.24π cm2
3.(2023黑龙江肇源期中)一个圆柱的底面圆半径扩大为原来的2倍,高缩小到原来的,它的侧面积 ( )
A.扩大为原来的2倍 B.缩小到原来的
C.不变 D.扩大为原来的4倍
4.如图,圆柱的母线长为10 cm,轴截面的面积为240 cm2,则圆柱的侧面积是 ( )
A.240 cm2 B.240π cm2
C.480 cm2 D.480π cm2
5.【教材变式·P148T3】(2022北京东城期末)如图所示,在长方形ABCD中,AB=a,BC=b,且a>b,将长方形ABCD绕边AB所在的直线旋转一周形成圆柱甲,将长方形ABCD绕边BC所在直线旋转一周形成圆柱乙,记两个圆柱的侧面积分别为S甲、S乙,则结论中正确的是 ( )
A.S甲>S乙 B.S甲
6.【最短距离问题】(2022浙江金华中考)如图,圆柱的底面圆直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最短路线,正确的是
( )
A. B. C. D.
7.已知圆柱的底面圆半径为2 cm,母线长为3 cm,则这个圆柱的表面积为 cm2.
8.一个底面圆直径是3厘米的圆柱,它的侧面展开是一个正方形,这个圆柱的高是 厘米.
9.【新独家原创】两个圆柱的侧面积相等,其中一个圆柱的高与另一圆柱的高的比为2∶1,求这两个圆柱的体积的比.
能力提升全练
10.【数学文化】(2023山东烟台期末,15,★★☆)我国古代有这样一道数学问题:“枯木一根直立地上,高三丈,周八尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何 ”题意是:如图所示,把枯木看成一个圆柱体,该圆柱的高为3丈,底面圆周长为8尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是
丈.(1丈=10尺)
11.(2022山东潍坊奎文一模,14,★★☆)云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的.如图所示的是公园内云顶滑雪场U型池的示意图,该场地可以看成是从一个长方体中挖去了半个圆柱而成的,它的横截面图中半圆的半径为 m,其边缘AB=CD=24 m,点E在CD上,CE=4 m.一名滑雪爱好者从点A滑到点E,他滑行的最短路线长为 m.
12.【最短距离问题】(2023四川广安中考,15,★★☆)如图,圆柱形玻璃杯的杯高为9 cm,底面圆周长为16 cm,在杯内壁离杯底4 cm的点A处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿1 cm,且与蜂蜜相对的点B处,则蚂蚁从外壁B处到内壁A处所走的最短路程为
cm.(杯壁厚度不计)
素养探究全练
13.【空间观念】如图1,O为圆柱形木块底面圆的圆心,过底面的一条弦AD,沿母线AB剖开,得剖面矩形ABCD,AD=24 cm,AB=25 cm.若的长为底面圆周长的,如图2所示.
(1)求☉O的半径;
(2)求这个圆柱形木块的表面积.(结果可保留π和根号)
答案全解全析
基础过关全练
1.D 圆柱的侧面展开图是矩形,故选D.
2.D 根据侧面积公式可得,S侧=2π×3×4=24π cm2,故选D.
3.C 设原来圆柱的底面圆半径为r,高为h,则原来的侧面积为2πrh,
底面圆半径扩大为原来的2倍后变为2r,高缩小到原来的变为h,
∴变化后的侧面积为2π·2r·h=2πrh,∴侧面积不变.故选C.
4.B ∵圆柱的母线长为10 cm,轴截面的面积为240 cm2,∴圆柱的底面圆直径是240÷10=24 cm,所以S侧=24π×10=240π cm2.故选B.
5.C ∵S甲=2π×b×a=2πab,S乙=2π×a×b=2πab,
∴S甲=S乙.故选C.
6.C 将圆柱侧面沿AC“剪开”,侧面展开图为矩形,∵圆柱的底面圆直径为AB,∴蚂蚁爬行的最短路线是C中的路线.
7.答案 20π
解析 S底=π×22=4π cm2,S侧=2π×2×3=12π cm2,
∴S表=2×4π+12π=8π+12π=20π cm2.
8.答案 3π
解析 ∵圆柱的底面圆直径是3厘米,
∴底面圆周长为π×3=3π厘米,
∵它的侧面展开是一个正方形,
∴圆柱的高是3π厘米.
9.解析 设两个圆柱的侧面积分别为S1,S2,底面圆半径分别为r1,r2,高分别为h1,h2(h1>h2),体积分别为V1,V2.则S1=2πr1h1,S2=2πr2h2.
∵侧面积相等,高的比为2∶1,
∴S1=S2,h1=2h2.
∴2πr1h1=2πr2h2.
∴r2=2r1.
∴===.
即这两个圆柱的体积的比为1∶2.
能力提升全练
10.答案 5
解析 如图所示,线段AB的长即为葛藤的最短长度,
∵8尺=0.8丈,
∴AC=0.8×5=4丈,
在Rt△ABC中,
AB===5丈.
11.答案 4
解析 如图,线段AE的长度即为他滑行的最短路线长.
根据题意可知AD=2π××=12(m),DE=CD-CE=24-4=20(m),
在Rt△ADE中,根据勾股定理,得
AE===4(m).
故他滑行的最短路线长为4 m.
12.答案 10
解析 如图,将杯子侧面展开,分别标注字母C、D、E、F,作点B关于CF的对称点B',连接AB'交CF于点P,连接BP,此时BP+AP的值最小,为AB'的长,即AB'为最短路径.
过点A作AG⊥CD,垂足为G,
由题意可得,AG=×16=8 cm,DG=AE=4 cm,
∵B'C=BC=1 cm,∴B'G=9-4+1=6 cm,
在Rt△AB'G中,AB'===10 cm.
∴蚂蚁从外壁B处到内壁A处所走的最短路程为10 cm.
方法解读 本题考查立体图形侧面上两点间的最短距离,但由于蜂蜜与蚂蚁的位置分别在杯子内外,故应先将圆柱的侧面展开,然后作点B(或点A)关于杯口展开直线的对称点,利用“将军饮马”模型结合勾股定理进行解答.
素养探究全练
13.解析 (1)如图,连接OA,OD,过O作OE⊥AD,垂足为E,
∵的长为底面圆周长的,
∴的度数为360°×=240°,
∴∠AOD=360°-240°=120°.
∵OE⊥AD,OA=OD,
∴∠AOE=×120°=60°,AE=AD=12 cm.
在Rt△AOE中,sin∠AOE=,即sin 60°=,
∴AO=8 cm,即☉O的半径为8 cm.
(2)设圆柱的表面积为S cm2,
则S=2S底+S侧=2π×+2π×8×25=384π+400π.
答:这个圆柱形木块的表面积为(384π+400π)cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
