8.1 中心投影课时练(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第8章 投影与识图
8.1 中心投影
基础过关全练
知识点 投影及中心投影
1.(2023广东深圳模拟)下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是( )
A. B.
C. D.
2.如图,某同学下晚自习后经过一路灯回寝室,他从A处背着灯柱方向走到B处,在这一过程中他在该路灯灯光下的影子 ( )
A.由长逐渐变短 B.由短逐渐变长
C.先变长后变短 D.先变短后变长
3.(2020浙江绍兴中考)如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2∶5,且三角板的一边长为8 cm,则投影三角板的对应边长为 ( )
A.20 cm B.10 cm C.8 cm D.3.2 cm
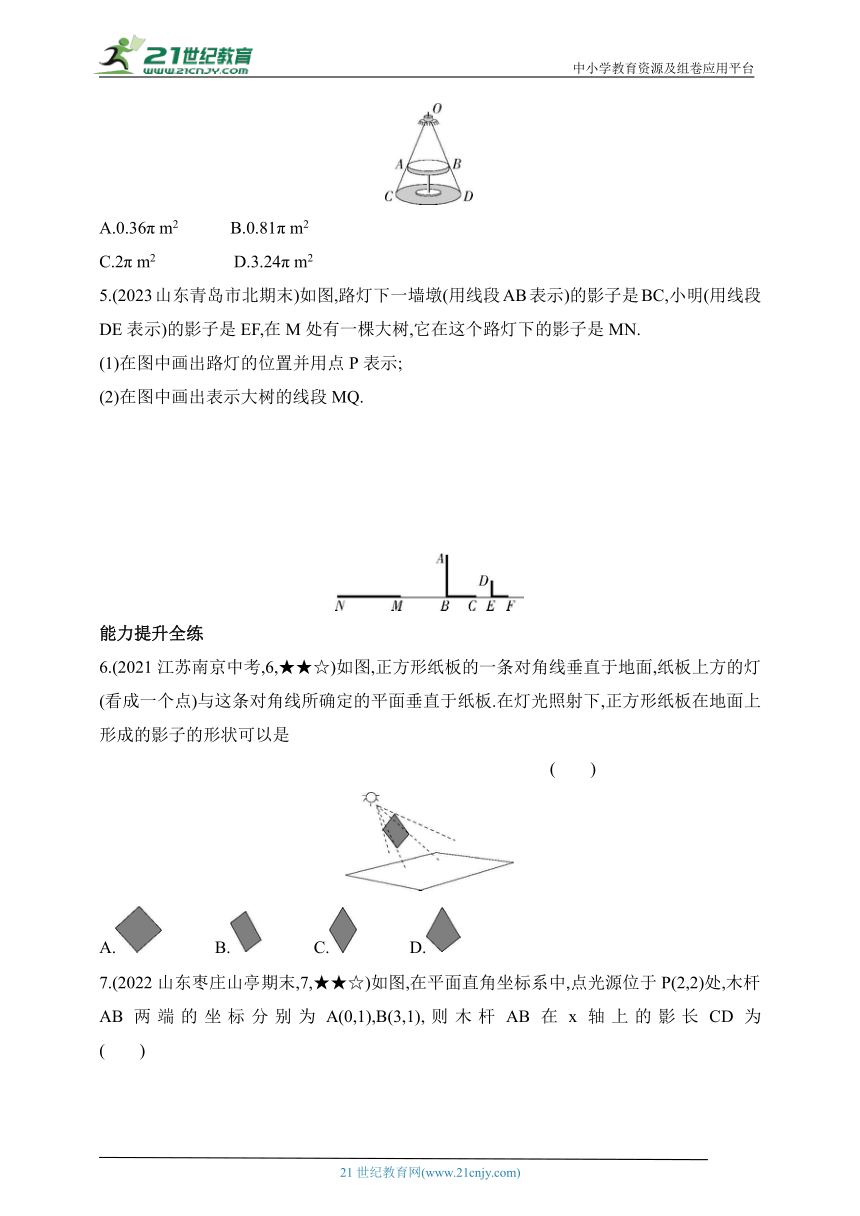
4.【教材变式·P163习题T3】如图所示的是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )
A.0.36π m2 B.0.81π m2
C.2π m2 D.3.24π m2
5.(2023山东青岛市北期末)如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一棵大树,它在这个路灯下的影子是MN.
(1)在图中画出路灯的位置并用点P表示;
(2)在图中画出表示大树的线段MQ.
能力提升全练
6.(2021江苏南京中考,6,★★☆)如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看成一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是
( )
A. B. C. D.
7.(2022山东枣庄山亭期末,7,★★☆)如图,在平面直角坐标系中,点光源位于P(2,2)处,木杆AB两端的坐标分别为A(0,1),B(3,1),则木杆AB在x轴上的影长CD为 ( )
A.3 B.5 C.6 D.7
8.(2023山东鄄城期末,9,★★☆)如图,小莉用灯泡O(看成一个点)照射一个矩形硬纸片ABCD,在墙上形成矩形影子A'B'C'D',现测得OA=
2 cm,OA'=5 cm,纸片ABCD的面积为8 cm2,则影子A'B'C'D'的面积为
cm2.
素养探究全练
9.【几何直观】(2022上海中考)我们经常会采用不同方法对某物体进行测量,请测量下列灯杆AB的长.
(1)如图1所示,将一个测角仪放置在距离灯杆AB底部a米的点D处,测角仪高为b米,从C点测得A点的仰角为α,求灯杆AB的高度.(用含a,b,α的代数式表示)
(2)我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图2所示,现将一高度为2米的木杆CG放在灯杆AB前,测得其影长CH为1米,再将木杆沿着BC方向移动1.8米至DE的位置,此时测得其影长DF为3米,求灯杆AB的高度.
答案全解全析
基础过关全练
1.D 路灯在中间,路灯和影子应该位于人的两边,不能位于同侧,符合题意的只有D选项,故选D.
2.B 根据中心投影的特征可知人远离灯光时,其影子逐渐变长.故选B.
3.A 设投影三角板的对应边长为x cm,∵三角板与投影三角板相似,∴8∶x=2∶5,解得x=20,故选A.
4.B 连接AB、CD,如图,
则△OAB∽△OCD.
设△OAB,△OCD的高分别为h1 m,h2 m,
则=,∴=,
∴CD=1.8 m,∴S阴影=π×=0.81π m2.
5.解析 (1)点P位置如图.
(2)线段MQ如图.
能力提升全练
6.D 正方形纸板的一条对角线垂直于地面,纸板上方的灯(看成一个点)与这条对角线所确定的平面垂直于纸板,设该条对角线为l,∵正方形是轴对称图形,对角线l所在的直线是其中一条对称轴,∴在地面上的投影关于对角线l的投影所在的直线对称.∵灯在纸板上方,∴上方投影比下方投影要长,故选D.
7.C 过P作PE⊥x轴于E,交AB于M,如图,
∵P(2,2),A(0,1),B(3,1),
∴PM=1,PE=2,AB=3,AB∥CD,
∴△PAB∽△PCD,
∴=,∴=,∴CD=6,故选C.
8.答案 50
解析 ∵AB∥A'B',∴△AOB∽△A'OB',
∴==.∴==,
又∵S矩形ABCD=8 cm2,∴S矩形A'B'C'D'==50(cm2).
素养探究全练
9.解析 (1)如图,
由题意得,BQ=CD=b米,QC=BD=a米,∠AQC=90°,∠ACQ=α,
在Rt△AQC中,
AQ=CQ·tan α=atan α(米),
∴AB=AQ+BQ=(atan α+b)米,
∴灯杆AB的高度为(atan α+b)米.
(2)∵∠ABC=∠GCD=∠EDF=90°,
∴CG∥AB,ED∥AB,∴=,=,
设AB=x米,BC=y米,则BH=(y+1)米,BF=y+1.8+3=(y+4.8)米.
∴解得
∴AB=3.8米,BC=0.9米.
∴灯杆AB的高度为3.8米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第8章 投影与识图
8.1 中心投影
基础过关全练
知识点 投影及中心投影
1.(2023广东深圳模拟)下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是( )
A. B.
C. D.
2.如图,某同学下晚自习后经过一路灯回寝室,他从A处背着灯柱方向走到B处,在这一过程中他在该路灯灯光下的影子 ( )
A.由长逐渐变短 B.由短逐渐变长
C.先变长后变短 D.先变短后变长
3.(2020浙江绍兴中考)如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2∶5,且三角板的一边长为8 cm,则投影三角板的对应边长为 ( )
A.20 cm B.10 cm C.8 cm D.3.2 cm
4.【教材变式·P163习题T3】如图所示的是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )
A.0.36π m2 B.0.81π m2
C.2π m2 D.3.24π m2
5.(2023山东青岛市北期末)如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一棵大树,它在这个路灯下的影子是MN.
(1)在图中画出路灯的位置并用点P表示;
(2)在图中画出表示大树的线段MQ.
能力提升全练
6.(2021江苏南京中考,6,★★☆)如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看成一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是
( )
A. B. C. D.
7.(2022山东枣庄山亭期末,7,★★☆)如图,在平面直角坐标系中,点光源位于P(2,2)处,木杆AB两端的坐标分别为A(0,1),B(3,1),则木杆AB在x轴上的影长CD为 ( )
A.3 B.5 C.6 D.7
8.(2023山东鄄城期末,9,★★☆)如图,小莉用灯泡O(看成一个点)照射一个矩形硬纸片ABCD,在墙上形成矩形影子A'B'C'D',现测得OA=
2 cm,OA'=5 cm,纸片ABCD的面积为8 cm2,则影子A'B'C'D'的面积为
cm2.
素养探究全练
9.【几何直观】(2022上海中考)我们经常会采用不同方法对某物体进行测量,请测量下列灯杆AB的长.
(1)如图1所示,将一个测角仪放置在距离灯杆AB底部a米的点D处,测角仪高为b米,从C点测得A点的仰角为α,求灯杆AB的高度.(用含a,b,α的代数式表示)
(2)我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图2所示,现将一高度为2米的木杆CG放在灯杆AB前,测得其影长CH为1米,再将木杆沿着BC方向移动1.8米至DE的位置,此时测得其影长DF为3米,求灯杆AB的高度.
答案全解全析
基础过关全练
1.D 路灯在中间,路灯和影子应该位于人的两边,不能位于同侧,符合题意的只有D选项,故选D.
2.B 根据中心投影的特征可知人远离灯光时,其影子逐渐变长.故选B.
3.A 设投影三角板的对应边长为x cm,∵三角板与投影三角板相似,∴8∶x=2∶5,解得x=20,故选A.
4.B 连接AB、CD,如图,
则△OAB∽△OCD.
设△OAB,△OCD的高分别为h1 m,h2 m,
则=,∴=,
∴CD=1.8 m,∴S阴影=π×=0.81π m2.
5.解析 (1)点P位置如图.
(2)线段MQ如图.
能力提升全练
6.D 正方形纸板的一条对角线垂直于地面,纸板上方的灯(看成一个点)与这条对角线所确定的平面垂直于纸板,设该条对角线为l,∵正方形是轴对称图形,对角线l所在的直线是其中一条对称轴,∴在地面上的投影关于对角线l的投影所在的直线对称.∵灯在纸板上方,∴上方投影比下方投影要长,故选D.
7.C 过P作PE⊥x轴于E,交AB于M,如图,
∵P(2,2),A(0,1),B(3,1),
∴PM=1,PE=2,AB=3,AB∥CD,
∴△PAB∽△PCD,
∴=,∴=,∴CD=6,故选C.
8.答案 50
解析 ∵AB∥A'B',∴△AOB∽△A'OB',
∴==.∴==,
又∵S矩形ABCD=8 cm2,∴S矩形A'B'C'D'==50(cm2).
素养探究全练
9.解析 (1)如图,
由题意得,BQ=CD=b米,QC=BD=a米,∠AQC=90°,∠ACQ=α,
在Rt△AQC中,
AQ=CQ·tan α=atan α(米),
∴AB=AQ+BQ=(atan α+b)米,
∴灯杆AB的高度为(atan α+b)米.
(2)∵∠ABC=∠GCD=∠EDF=90°,
∴CG∥AB,ED∥AB,∴=,=,
设AB=x米,BC=y米,则BH=(y+1)米,BF=y+1.8+3=(y+4.8)米.
∴解得
∴AB=3.8米,BC=0.9米.
∴灯杆AB的高度为3.8米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
