8.2 平行投影课时练(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第8章 投影与识图
8.2 平行投影
基础过关全练
知识点1 平行投影
1.(2023广西柳州柳南二模)房间窗户的边框形状是矩形,在阳光的照射下边框在房间地面上形成了投影,则投影的形状可能是
( )
A.圆 B.椭圆
C.三角形 D.平行四边形
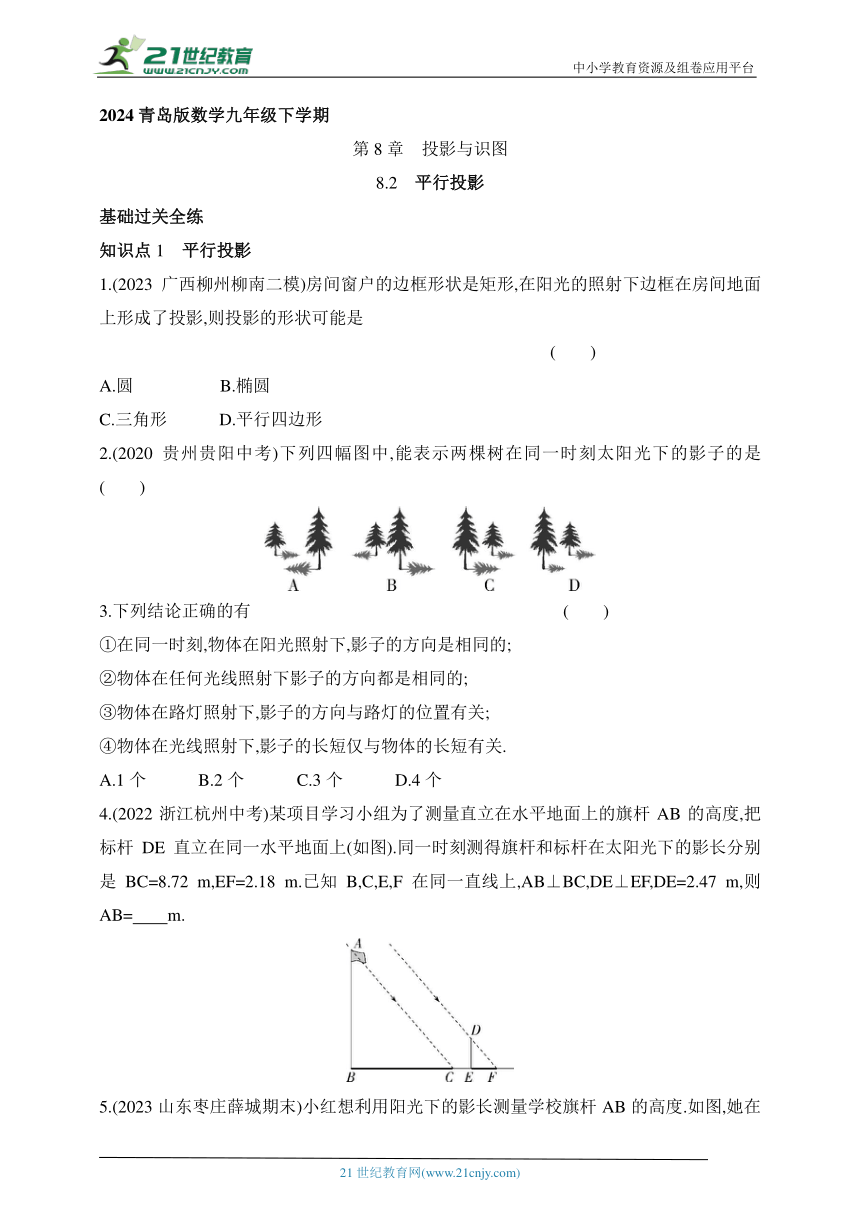
2.(2020贵州贵阳中考)下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的是( )
3.下列结论正确的有 ( )
①在同一时刻,物体在阳光照射下,影子的方向是相同的;
②物体在任何光线照射下影子的方向都是相同的;
③物体在路灯照射下,影子的方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个 B.2个 C.3个 D.4个
4.(2022浙江杭州中考)某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72 m,EF=2.18 m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47 m,则AB= m.
5.(2023山东枣庄薛城期末)小红想利用阳光下的影长测量学校旗杆AB的高度.如图,她在某一时刻在地面上竖直立一根2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在阳光下的投影BF;
(2)如果BF=1.6米,求旗杆AB的高.
知识点2 正投影
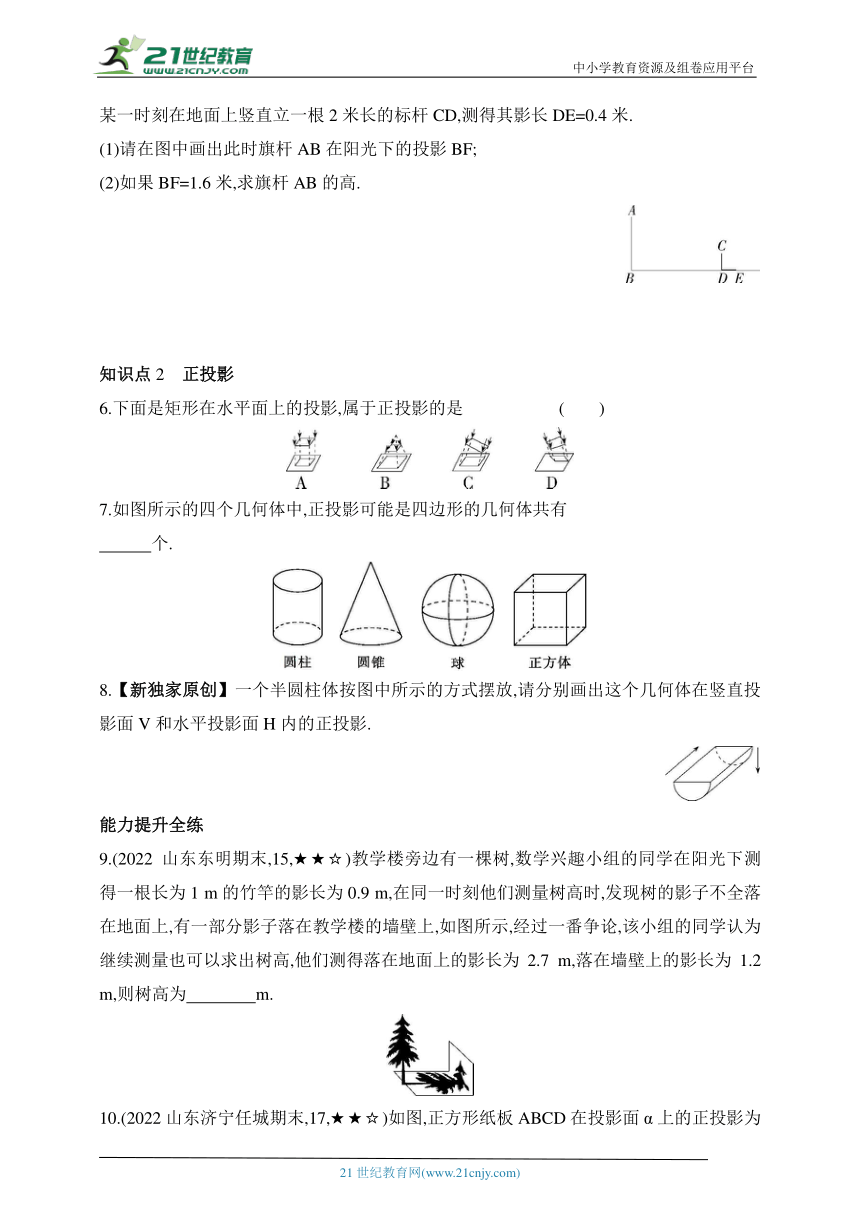
6.下面是矩形在水平面上的投影,属于正投影的是 ( )
7.如图所示的四个几何体中,正投影可能是四边形的几何体共有
个.
8.【新独家原创】一个半圆柱体按图中所示的方式摆放,请分别画出这个几何体在竖直投影面V和水平投影面H内的正投影.
能力提升全练
9.(2022山东东明期末,15,★★☆)教学楼旁边有一棵树,数学兴趣小组的同学在阳光下测得一根长为1 m的竹竿的影长为0.9 m,在同一时刻他们测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图所示,经过一番争论,该小组的同学认为继续测量也可以求出树高,他们测得落在地面上的影长为2.7 m,落在墙壁上的影长为1.2 m,则树高为 m.
10.(2022山东济宁任城期末,17,★★☆)如图,正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,其中边AB、CD与投影面平行,AD,BC与投影面不平行.若正方形ABCD的边长为5 cm,∠BCC1=45°,求其投影A1B1C1D1的面积.
素养探究全练
11.【几何直观】(2023山东曹县期末)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别为BC,CD,测得BC=4米,CD=4米,坡面CD的坡度i=1∶,在D处测得电线杆顶端A的仰角为30°,求电线杆AB的高度.
12.【应用意识】如图,一幢楼房AB背后有一台阶CD,台阶每层高0.2 m,且AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在台阶的MN这层上晒太阳.
(1)楼房的高度约为多少米 (参考数据:≈1.732.结果精确到0.1 m)
(2)过了一会儿,当α=45°时,小猫能否晒到太阳 请说明理由.
答案全解全析
基础过关全练
1.D 因为矩形边框的对边平行,所以在阳光的照射下边框在房间地面上形成的投影的对边也平行或重合,所以投影的形状不可能为三角形、圆、椭圆,可能是平行四边形,故选D.
2.C A,B选项,两棵树的影子的方向相反,不可能为同一时刻太阳光下的影子;C选项,两棵树的影子的方向相同,且较高的树的影子长,符合题意;D选项,两棵树的影子的方向相同,但较高的树的影子比较矮的树的影子短,不符合题意.故选C.
3.B ①由于太阳光线是平行光线,所以物体在同一时刻阳光照射下,影子的方向是相同的,故①正确;②物体在灯光的照射下影子的方向与物体的位置有关,故②错误;③物体在路灯照射下,影子的方向与路灯的位置有关,故③正确;④物体在点光源的照射下,影子的长短与物体的长短和点光源的位置有关,故④错误.所以正确的有①和③,共2个,故选B.
4.答案 9.88
解析 由题意可得,=,即=,
∴AB=9.88 m.
5.解析 (1)连接CE,过A点作AF∥CE交BD于F,则BF即为所求,如图.
(2)∵AF∥CE,∴∠AFB=∠CED,
又∵∠ABF=∠CDE=90°,∴△ABF∽△CDE,
∴=,即=,∴AB=8米.
答:旗杆AB的高为8米.
6.A 正投影要求投射线与投影面之间是互相垂直的,只有选项A符合题意.
7.答案 2
解析 圆柱和正方体的正投影可能是四边形,圆锥和球的正投影不可能是四边形,所以正投影可能是四边形的几何体是圆柱和正方体,共2个.
8.解析 如图所示.
能力提升全练
9.答案 4.2
解析 根据题意,画出示意图如图,过点C作CE∥AD,交AB于E,
∵AE∥CD,AD∥EC,
∴四边形AECD是平行四边形,∴AE=CD=1.2 m.
由题意,得△EBC∽△PQR,
∴=,即=,∴BE=3 m.
∴AB=BE+AE=3+1.2=4.2(m),
故树高为4.2 m.
10.解析 过B点作BH⊥CC1于H,如图,由题意知,BC=5 cm,
∵∠BCC1=45°,∴BH=BC= cm,∵正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,∴B1C1=BH= cm,C1D1=CD=5 cm,∴四边形A1B1C1D1的面积=×5=(cm2).
素养探究全练
11.解析 如图,过D作DE⊥BC交BC的延长线于点E,过D作DF⊥AB于点F,
∵CD的坡度i=1∶,
∴设DE=x米,则CE=x米,
在Rt△CDE中,DE2+CE2=CD2,
∴x2+=42,∴x=2,
∴BF=DE=2米,CE=2米,
∴DF=BE=BC+CE=4+2=6(米),
由题意知∠ADF=30°,在Rt△ADF中,
AF=DF·tan 30°=6×=6(米),
∴AB=AF+BF=6+2=8(米).
答:电线杆AB的高度为8米.
12.解析 (1)当α=60°时,在Rt△ABE中,易知∠ABE=30°,
∴BE=2AE=20 m.
∴AB==10≈17.3(m).
答:楼房的高度约为17.3 m.
(2)当α=45°时,小猫能晒到太阳.
理由:假设没有台阶,如图,当α=45°时,
经过点B的光线与地面AD的交点为点F,
与MC的交点为点H.
∵∠BFA=45°,∴∠ABF=∠BFA=45°.
∴AF=AB=17.3 m,
∴CF=AF-AC=17.3-17.2=0.1(m).
易知CH=CF=0.1 m<0.2 m,
∴楼房的影子落在台阶MC这个侧面上.
∴小猫能晒到太阳.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第8章 投影与识图
8.2 平行投影
基础过关全练
知识点1 平行投影
1.(2023广西柳州柳南二模)房间窗户的边框形状是矩形,在阳光的照射下边框在房间地面上形成了投影,则投影的形状可能是
( )
A.圆 B.椭圆
C.三角形 D.平行四边形
2.(2020贵州贵阳中考)下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的是( )
3.下列结论正确的有 ( )
①在同一时刻,物体在阳光照射下,影子的方向是相同的;
②物体在任何光线照射下影子的方向都是相同的;
③物体在路灯照射下,影子的方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个 B.2个 C.3个 D.4个
4.(2022浙江杭州中考)某项目学习小组为了测量直立在水平地面上的旗杆AB的高度,把标杆DE直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC=8.72 m,EF=2.18 m.已知B,C,E,F在同一直线上,AB⊥BC,DE⊥EF,DE=2.47 m,则AB= m.
5.(2023山东枣庄薛城期末)小红想利用阳光下的影长测量学校旗杆AB的高度.如图,她在某一时刻在地面上竖直立一根2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在阳光下的投影BF;
(2)如果BF=1.6米,求旗杆AB的高.
知识点2 正投影
6.下面是矩形在水平面上的投影,属于正投影的是 ( )
7.如图所示的四个几何体中,正投影可能是四边形的几何体共有
个.
8.【新独家原创】一个半圆柱体按图中所示的方式摆放,请分别画出这个几何体在竖直投影面V和水平投影面H内的正投影.
能力提升全练
9.(2022山东东明期末,15,★★☆)教学楼旁边有一棵树,数学兴趣小组的同学在阳光下测得一根长为1 m的竹竿的影长为0.9 m,在同一时刻他们测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图所示,经过一番争论,该小组的同学认为继续测量也可以求出树高,他们测得落在地面上的影长为2.7 m,落在墙壁上的影长为1.2 m,则树高为 m.
10.(2022山东济宁任城期末,17,★★☆)如图,正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,其中边AB、CD与投影面平行,AD,BC与投影面不平行.若正方形ABCD的边长为5 cm,∠BCC1=45°,求其投影A1B1C1D1的面积.
素养探究全练
11.【几何直观】(2023山东曹县期末)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别为BC,CD,测得BC=4米,CD=4米,坡面CD的坡度i=1∶,在D处测得电线杆顶端A的仰角为30°,求电线杆AB的高度.
12.【应用意识】如图,一幢楼房AB背后有一台阶CD,台阶每层高0.2 m,且AC=17.2 m,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10 m,现有一只小猫睡在台阶的MN这层上晒太阳.
(1)楼房的高度约为多少米 (参考数据:≈1.732.结果精确到0.1 m)
(2)过了一会儿,当α=45°时,小猫能否晒到太阳 请说明理由.
答案全解全析
基础过关全练
1.D 因为矩形边框的对边平行,所以在阳光的照射下边框在房间地面上形成的投影的对边也平行或重合,所以投影的形状不可能为三角形、圆、椭圆,可能是平行四边形,故选D.
2.C A,B选项,两棵树的影子的方向相反,不可能为同一时刻太阳光下的影子;C选项,两棵树的影子的方向相同,且较高的树的影子长,符合题意;D选项,两棵树的影子的方向相同,但较高的树的影子比较矮的树的影子短,不符合题意.故选C.
3.B ①由于太阳光线是平行光线,所以物体在同一时刻阳光照射下,影子的方向是相同的,故①正确;②物体在灯光的照射下影子的方向与物体的位置有关,故②错误;③物体在路灯照射下,影子的方向与路灯的位置有关,故③正确;④物体在点光源的照射下,影子的长短与物体的长短和点光源的位置有关,故④错误.所以正确的有①和③,共2个,故选B.
4.答案 9.88
解析 由题意可得,=,即=,
∴AB=9.88 m.
5.解析 (1)连接CE,过A点作AF∥CE交BD于F,则BF即为所求,如图.
(2)∵AF∥CE,∴∠AFB=∠CED,
又∵∠ABF=∠CDE=90°,∴△ABF∽△CDE,
∴=,即=,∴AB=8米.
答:旗杆AB的高为8米.
6.A 正投影要求投射线与投影面之间是互相垂直的,只有选项A符合题意.
7.答案 2
解析 圆柱和正方体的正投影可能是四边形,圆锥和球的正投影不可能是四边形,所以正投影可能是四边形的几何体是圆柱和正方体,共2个.
8.解析 如图所示.
能力提升全练
9.答案 4.2
解析 根据题意,画出示意图如图,过点C作CE∥AD,交AB于E,
∵AE∥CD,AD∥EC,
∴四边形AECD是平行四边形,∴AE=CD=1.2 m.
由题意,得△EBC∽△PQR,
∴=,即=,∴BE=3 m.
∴AB=BE+AE=3+1.2=4.2(m),
故树高为4.2 m.
10.解析 过B点作BH⊥CC1于H,如图,由题意知,BC=5 cm,
∵∠BCC1=45°,∴BH=BC= cm,∵正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,∴B1C1=BH= cm,C1D1=CD=5 cm,∴四边形A1B1C1D1的面积=×5=(cm2).
素养探究全练
11.解析 如图,过D作DE⊥BC交BC的延长线于点E,过D作DF⊥AB于点F,
∵CD的坡度i=1∶,
∴设DE=x米,则CE=x米,
在Rt△CDE中,DE2+CE2=CD2,
∴x2+=42,∴x=2,
∴BF=DE=2米,CE=2米,
∴DF=BE=BC+CE=4+2=6(米),
由题意知∠ADF=30°,在Rt△ADF中,
AF=DF·tan 30°=6×=6(米),
∴AB=AF+BF=6+2=8(米).
答:电线杆AB的高度为8米.
12.解析 (1)当α=60°时,在Rt△ABE中,易知∠ABE=30°,
∴BE=2AE=20 m.
∴AB==10≈17.3(m).
答:楼房的高度约为17.3 m.
(2)当α=45°时,小猫能晒到太阳.
理由:假设没有台阶,如图,当α=45°时,
经过点B的光线与地面AD的交点为点F,
与MC的交点为点H.
∵∠BFA=45°,∴∠ABF=∠BFA=45°.
∴AF=AB=17.3 m,
∴CF=AF-AC=17.3-17.2=0.1(m).
易知CH=CF=0.1 m<0.2 m,
∴楼房的影子落在台阶MC这个侧面上.
∴小猫能晒到太阳.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
