第7章 空间图形的初步认识素养综合检测试题(含解析)
文档属性
| 名称 | 第7章 空间图形的初步认识素养综合检测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 466.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 21:03:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第7章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
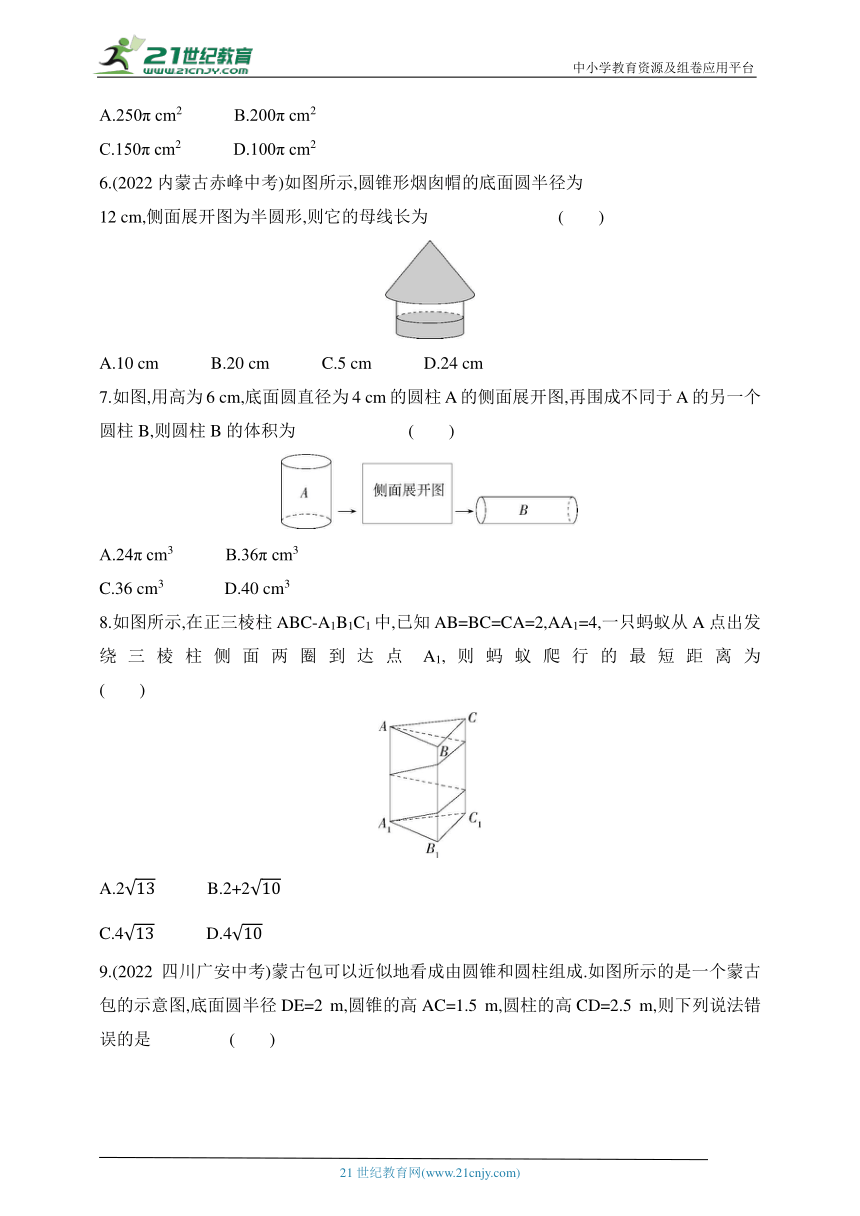
1.(2023江苏江阴期末)下列几何体的表面中,不含有曲面的是 ( )
A.圆柱 B.四棱柱 C.圆锥 D.球体
2.(2022山东临沂中考)如图所示的三棱柱的展开图不可能是 ( )
A B C D
3.(2023湖北宜昌中考)“争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片.”如图所示的是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是 ( )
A.文 B.明 C.典 D.范
4.(2023四川广元中考)向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量v的函数关系的大致图象是 ( )
A. B. C. D.
5.一个圆柱的高为10 cm,底面积为25π cm2,这个圆柱的表面积为
( )
A.250π cm2 B.200π cm2
C.150π cm2 D.100π cm2
6.(2022内蒙古赤峰中考)如图所示,圆锥形烟囱帽的底面圆半径为
12 cm,侧面展开图为半圆形,则它的母线长为 ( )
A.10 cm B.20 cm C.5 cm D.24 cm
7.如图,用高为6 cm,底面圆直径为4 cm的圆柱A的侧面展开图,再围成不同于A的另一个圆柱B,则圆柱B的体积为 ( )
A.24π cm3 B.36π cm3
C.36 cm3 D.40 cm3
8.如图所示,在正三棱柱ABC-A1B1C1中,已知AB=BC=CA=2,AA1=4,一只蚂蚁从A点出发绕三棱柱侧面两圈到达点A1,则蚂蚁爬行的最短距离为 ( )
A.2 B.2+2
C.4 D.4
9.(2022四川广安中考)蒙古包可以近似地看成由圆锥和圆柱组成.如图所示的是一个蒙古包的示意图,底面圆半径DE=2 m,圆锥的高AC=1.5 m,圆柱的高CD=2.5 m,则下列说法错误的是 ( )
A.圆柱的底面积为4π m2
B.圆柱的侧面积为10π m2
C.圆锥的母线AB长为2.25 m
D.圆锥的侧面积为5π m2
10.(2022山东单县期末)如图所示的四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,下列说法正确的有 ( )
①n棱柱有n个面;
②n棱柱有3n条棱;
③n棱柱有2n个顶点.
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题4分,共16分)
11.如图所示,用经过A、B、C三点的平面截去正方体的一角,变成一个新的多面体,若这个多面体的面数为m,棱数为n,则m+n= .
12.【新独家原创】一个直n棱柱,它的底面是边长为2 cm的正多边形,侧棱长是6 cm,侧面积是72 cm2,则n= .
13.一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面圆直径与高的比是 .
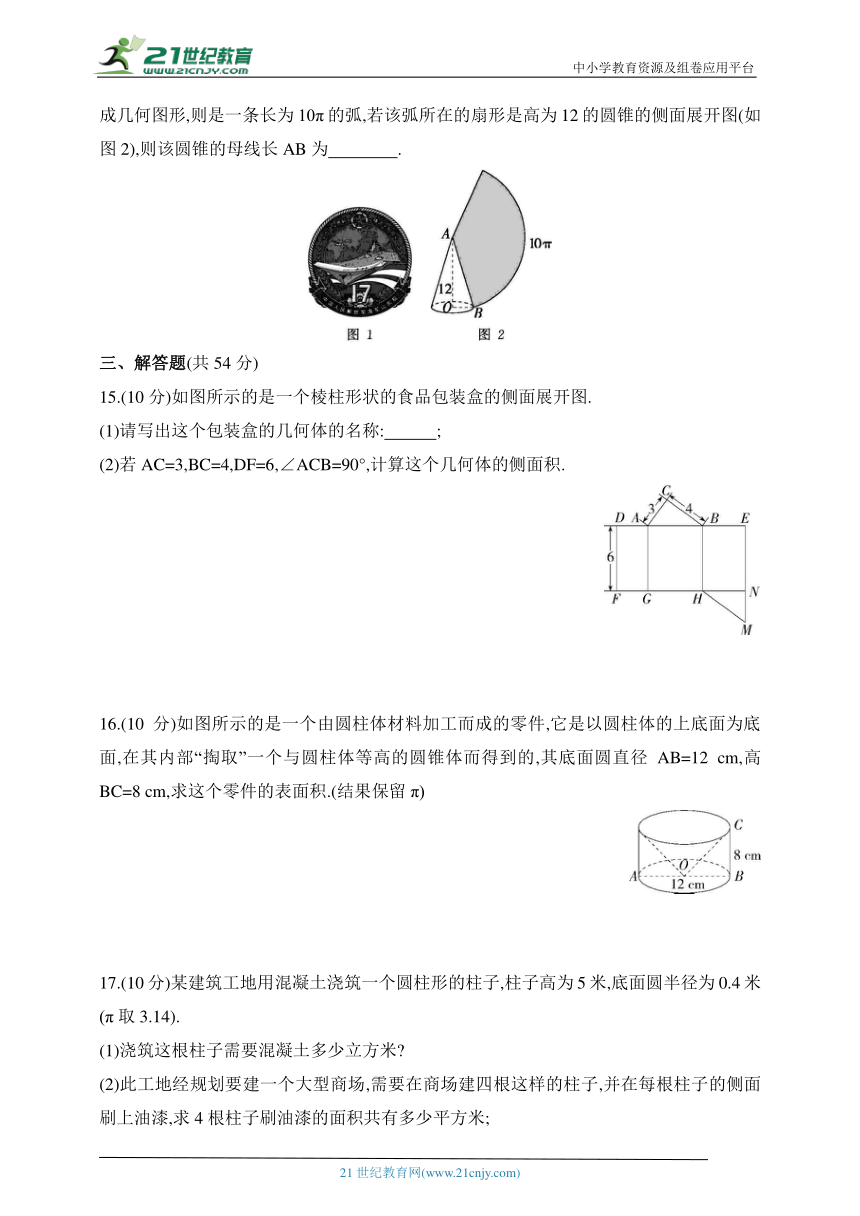
14.【国防教育】(2020湖南邵阳中考)图1是山东舰舰徽的构图,采用航母45度破浪而出的角度,展现山东舰作为中国首艘国产航母横空出世的气势,若将舰徽中第一条波浪抽象成几何图形,则是一条长为10π的弧,若该弧所在的扇形是高为12的圆锥的侧面展开图(如图2),则该圆锥的母线长AB为 .
三、解答题(共54分)
15.(10分)如图所示的是一个棱柱形状的食品包装盒的侧面展开图.
(1)请写出这个包装盒的几何体的名称: ;
(2)若AC=3,BC=4,DF=6,∠ACB=90°,计算这个几何体的侧面积.
16.(10分)如图所示的是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面圆直径AB=12 cm,高BC=8 cm,求这个零件的表面积.(结果保留π)
17.(10分)某建筑工地用混凝土浇筑一个圆柱形的柱子,柱子高为5米,底面圆半径为0.4米(π取3.14).
(1)浇筑这根柱子需要混凝土多少立方米
(2)此工地经规划要建一个大型商场,需要在商场建四根这样的柱子,并在每根柱子的侧面刷上油漆,求4根柱子刷油漆的面积共有多少平方米;
(3)在(2)的条件下,每平方米油漆的费用是40元,同时每平方米需要人工费5元,求4根柱子刷油漆共需多少元.
18.【一题多解】(12分)如图所示的是一个纸杯,AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6 cm,下底面直径为4 cm,EF=9 cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
19.(12分)已知用圆心角为120°,面积为3π的扇形卷成一个无底圆锥形筒.
(1)求这个圆锥形筒的高;
(2)一只蚂蚁要从圆锥底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC的中点D,求蚂蚁爬行的最短路程.
答案全解全析
1.B 圆柱和圆锥的侧面是曲面,球体的表面是曲面,只有四棱柱的6个面都是平面,故选B.
2.D 三棱柱的展开图中,上、下底面两个三角形不可能在同侧,故不可能是D选项.
3.B 将题图中的平面展开图还原成正方体可知,“城”字对面的字是“明”.故选B.
4.D 依据题意,从容器的构造形状上看,从底部到顶部的变化关系为开始宽,逐渐细小,再变宽.则注水量v随水深h的变化关系为先慢再快,最后又变慢.从函数的图象上看,只有D符合条件.
5.C 设底面圆半径为r cm,
由题意知πr2=25π,∴r=5,
则S侧=2×π×5×10=100π cm2,
∴S表=25π×2+100π=150π cm2.
故选C.
6.D 设母线长为l cm,由题意得,×2πl=2π×12,
解得l=24,∴母线长为24 cm,故选D.
7.C 根据题意,得到另一个圆柱B的底面圆周长是6 cm,高是4π cm,则圆柱B的体积为π××4π=36 cm3.故选C.
8.D 如图,大矩形对角线的长即为蚂蚁爬行的最短距离,
蚂蚁爬行的最短距离==4,故选D.
9.C ∵底面圆半径DE=2 m,∴圆柱的底面积为4π m2,故选项A正确;∵圆柱的高CD=2.5 m,∴圆柱的侧面积=2π×2×2.5=10π m2,故选项B正确;∵底面圆半径DE=2 m,∴BC=2 m,∵圆锥的高AC=1.5 m,∴圆锥的母线AB的长==2.5 m,故选项C错误;圆锥的侧面积=×2π×2×2.5=5π m2,故选项D正确.故说法错误的是选项C.
10.C ∵三棱柱有5个面,9条棱,6个顶点;四棱柱有6个面,12条棱,8个顶点;五棱柱有7个面,15条棱,10个顶点;……,∴n棱柱有(n+2)个面,3n条棱,2n个顶点,故选C.
11.答案 19
解析 由题图可得,新的多面体的面数增加1,棱数不变,所以m=7,n=12.所以m+n=7+12=19.
12.答案 6
解析 根据题意得2n×6=72,解得n=6.
13.答案 1∶π
解析 设圆柱的底面圆直径为d,高为h,
∵一个圆柱的侧面展开图是一个正方形,
∴πd=h,∴d∶h=1∶π,
即这个圆柱的底面圆直径与高的比是1∶π.
14.答案 13
解析 设圆锥的底面圆半径为r,
根据题意得2πr=10π,解得r=5,
在Rt△AOB中,AB===13,
所以该圆锥的母线长AB为13.
15.解析 (1)三棱柱.
(2)∵AC=3,BC=4,∠ACB=90°,
∴AB==5,
又∵DF=6,∴S侧=(3+4+5)×6=72,
即这个几何体的侧面积为72.
16.解析 圆柱的底面圆半径=12÷2=6 cm,
∴圆柱的底面积=π×62=36π cm2.
圆柱的侧面积=12π×8=96π cm2,
圆锥母线长==10 cm,
∴圆锥的侧面积=π×6×10=60π cm2.
∴这个零件的表面积为36π+96π+60π=192π cm2.
17.解析 (1)π×0.42×5=2.512(立方米).
答:浇筑这根柱子需要混凝土2.512立方米.
(2)4×2π×0.4×5=50.24(平方米).
答:4根柱子刷油漆的面积共有50.24平方米.
(3)50.24×(40+5)=2 260.8(元).
答:4根柱子刷油漆共需2 260.8元.
18.解析 解法一:设∠AOB=n°,OC=l cm,则OA=(l+9)cm,
根据题意得,
解得
∴这个扇形OAB的圆心角是40度.
∵S扇形OCD=×4π×18=36π cm2,
S扇形OAB=×6π×(18+9)=81π cm2,
∴纸杯的侧面积=S扇形OAB-S扇形OCD=81π-36π=45π cm2,
∵纸杯的底面积=π×=4π cm2,
∴纸杯的表面积=45π+4π=49π cm2.
解法二:∵=,∠COF=∠AOE,
∴△OCF∽△OAE.∴=.
∴=.∴OC=18(cm).
设∠AOB=n°,则=4π,解得n=40,
∴这个扇形OAB的圆心角是40度.
∵S扇形OCD=×4π×18=36π cm2,
S扇形OAB=×6π×(18+9)=81π cm2,
∴纸杯的侧面积=S扇形OAB-S扇形OCD=81π-36π=45π cm2,
∵纸杯的底面积=π×=4π cm2,
∴纸杯的表面积=45π+4π=49π cm2.
19.解析 (1)设圆锥的母线长为l,底面圆半径为r,高为h,根据题意得3π=,∴l=3,∴πr×3=3π.解得r=1,∴h==2,故这个圆锥形筒的高为2.
(2)如图,画出这个圆锥的侧面展开图,连接BC、BD,则BD的长为蚂蚁爬行的最短路程.
由题意可知,∠BAC=120°÷2=60°,
∵AB=AC,
∴△ABC为等边三角形.
∵D为AC的中点,
∴BD⊥AC.
在Rt△ABD中,BD=AB·sin 60°=3×=.
故蚂蚁爬行的最短路程为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第7章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023江苏江阴期末)下列几何体的表面中,不含有曲面的是 ( )
A.圆柱 B.四棱柱 C.圆锥 D.球体
2.(2022山东临沂中考)如图所示的三棱柱的展开图不可能是 ( )
A B C D
3.(2023湖北宜昌中考)“争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片.”如图所示的是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是 ( )
A.文 B.明 C.典 D.范
4.(2023四川广元中考)向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量v的函数关系的大致图象是 ( )
A. B. C. D.
5.一个圆柱的高为10 cm,底面积为25π cm2,这个圆柱的表面积为
( )
A.250π cm2 B.200π cm2
C.150π cm2 D.100π cm2
6.(2022内蒙古赤峰中考)如图所示,圆锥形烟囱帽的底面圆半径为
12 cm,侧面展开图为半圆形,则它的母线长为 ( )
A.10 cm B.20 cm C.5 cm D.24 cm
7.如图,用高为6 cm,底面圆直径为4 cm的圆柱A的侧面展开图,再围成不同于A的另一个圆柱B,则圆柱B的体积为 ( )
A.24π cm3 B.36π cm3
C.36 cm3 D.40 cm3
8.如图所示,在正三棱柱ABC-A1B1C1中,已知AB=BC=CA=2,AA1=4,一只蚂蚁从A点出发绕三棱柱侧面两圈到达点A1,则蚂蚁爬行的最短距离为 ( )
A.2 B.2+2
C.4 D.4
9.(2022四川广安中考)蒙古包可以近似地看成由圆锥和圆柱组成.如图所示的是一个蒙古包的示意图,底面圆半径DE=2 m,圆锥的高AC=1.5 m,圆柱的高CD=2.5 m,则下列说法错误的是 ( )
A.圆柱的底面积为4π m2
B.圆柱的侧面积为10π m2
C.圆锥的母线AB长为2.25 m
D.圆锥的侧面积为5π m2
10.(2022山东单县期末)如图所示的四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,下列说法正确的有 ( )
①n棱柱有n个面;
②n棱柱有3n条棱;
③n棱柱有2n个顶点.
A.0个 B.1个 C.2个 D.3个
二、填空题(每小题4分,共16分)
11.如图所示,用经过A、B、C三点的平面截去正方体的一角,变成一个新的多面体,若这个多面体的面数为m,棱数为n,则m+n= .
12.【新独家原创】一个直n棱柱,它的底面是边长为2 cm的正多边形,侧棱长是6 cm,侧面积是72 cm2,则n= .
13.一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面圆直径与高的比是 .
14.【国防教育】(2020湖南邵阳中考)图1是山东舰舰徽的构图,采用航母45度破浪而出的角度,展现山东舰作为中国首艘国产航母横空出世的气势,若将舰徽中第一条波浪抽象成几何图形,则是一条长为10π的弧,若该弧所在的扇形是高为12的圆锥的侧面展开图(如图2),则该圆锥的母线长AB为 .
三、解答题(共54分)
15.(10分)如图所示的是一个棱柱形状的食品包装盒的侧面展开图.
(1)请写出这个包装盒的几何体的名称: ;
(2)若AC=3,BC=4,DF=6,∠ACB=90°,计算这个几何体的侧面积.
16.(10分)如图所示的是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面圆直径AB=12 cm,高BC=8 cm,求这个零件的表面积.(结果保留π)
17.(10分)某建筑工地用混凝土浇筑一个圆柱形的柱子,柱子高为5米,底面圆半径为0.4米(π取3.14).
(1)浇筑这根柱子需要混凝土多少立方米
(2)此工地经规划要建一个大型商场,需要在商场建四根这样的柱子,并在每根柱子的侧面刷上油漆,求4根柱子刷油漆的面积共有多少平方米;
(3)在(2)的条件下,每平方米油漆的费用是40元,同时每平方米需要人工费5元,求4根柱子刷油漆共需多少元.
18.【一题多解】(12分)如图所示的是一个纸杯,AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6 cm,下底面直径为4 cm,EF=9 cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
19.(12分)已知用圆心角为120°,面积为3π的扇形卷成一个无底圆锥形筒.
(1)求这个圆锥形筒的高;
(2)一只蚂蚁要从圆锥底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC的中点D,求蚂蚁爬行的最短路程.
答案全解全析
1.B 圆柱和圆锥的侧面是曲面,球体的表面是曲面,只有四棱柱的6个面都是平面,故选B.
2.D 三棱柱的展开图中,上、下底面两个三角形不可能在同侧,故不可能是D选项.
3.B 将题图中的平面展开图还原成正方体可知,“城”字对面的字是“明”.故选B.
4.D 依据题意,从容器的构造形状上看,从底部到顶部的变化关系为开始宽,逐渐细小,再变宽.则注水量v随水深h的变化关系为先慢再快,最后又变慢.从函数的图象上看,只有D符合条件.
5.C 设底面圆半径为r cm,
由题意知πr2=25π,∴r=5,
则S侧=2×π×5×10=100π cm2,
∴S表=25π×2+100π=150π cm2.
故选C.
6.D 设母线长为l cm,由题意得,×2πl=2π×12,
解得l=24,∴母线长为24 cm,故选D.
7.C 根据题意,得到另一个圆柱B的底面圆周长是6 cm,高是4π cm,则圆柱B的体积为π××4π=36 cm3.故选C.
8.D 如图,大矩形对角线的长即为蚂蚁爬行的最短距离,
蚂蚁爬行的最短距离==4,故选D.
9.C ∵底面圆半径DE=2 m,∴圆柱的底面积为4π m2,故选项A正确;∵圆柱的高CD=2.5 m,∴圆柱的侧面积=2π×2×2.5=10π m2,故选项B正确;∵底面圆半径DE=2 m,∴BC=2 m,∵圆锥的高AC=1.5 m,∴圆锥的母线AB的长==2.5 m,故选项C错误;圆锥的侧面积=×2π×2×2.5=5π m2,故选项D正确.故说法错误的是选项C.
10.C ∵三棱柱有5个面,9条棱,6个顶点;四棱柱有6个面,12条棱,8个顶点;五棱柱有7个面,15条棱,10个顶点;……,∴n棱柱有(n+2)个面,3n条棱,2n个顶点,故选C.
11.答案 19
解析 由题图可得,新的多面体的面数增加1,棱数不变,所以m=7,n=12.所以m+n=7+12=19.
12.答案 6
解析 根据题意得2n×6=72,解得n=6.
13.答案 1∶π
解析 设圆柱的底面圆直径为d,高为h,
∵一个圆柱的侧面展开图是一个正方形,
∴πd=h,∴d∶h=1∶π,
即这个圆柱的底面圆直径与高的比是1∶π.
14.答案 13
解析 设圆锥的底面圆半径为r,
根据题意得2πr=10π,解得r=5,
在Rt△AOB中,AB===13,
所以该圆锥的母线长AB为13.
15.解析 (1)三棱柱.
(2)∵AC=3,BC=4,∠ACB=90°,
∴AB==5,
又∵DF=6,∴S侧=(3+4+5)×6=72,
即这个几何体的侧面积为72.
16.解析 圆柱的底面圆半径=12÷2=6 cm,
∴圆柱的底面积=π×62=36π cm2.
圆柱的侧面积=12π×8=96π cm2,
圆锥母线长==10 cm,
∴圆锥的侧面积=π×6×10=60π cm2.
∴这个零件的表面积为36π+96π+60π=192π cm2.
17.解析 (1)π×0.42×5=2.512(立方米).
答:浇筑这根柱子需要混凝土2.512立方米.
(2)4×2π×0.4×5=50.24(平方米).
答:4根柱子刷油漆的面积共有50.24平方米.
(3)50.24×(40+5)=2 260.8(元).
答:4根柱子刷油漆共需2 260.8元.
18.解析 解法一:设∠AOB=n°,OC=l cm,则OA=(l+9)cm,
根据题意得,
解得
∴这个扇形OAB的圆心角是40度.
∵S扇形OCD=×4π×18=36π cm2,
S扇形OAB=×6π×(18+9)=81π cm2,
∴纸杯的侧面积=S扇形OAB-S扇形OCD=81π-36π=45π cm2,
∵纸杯的底面积=π×=4π cm2,
∴纸杯的表面积=45π+4π=49π cm2.
解法二:∵=,∠COF=∠AOE,
∴△OCF∽△OAE.∴=.
∴=.∴OC=18(cm).
设∠AOB=n°,则=4π,解得n=40,
∴这个扇形OAB的圆心角是40度.
∵S扇形OCD=×4π×18=36π cm2,
S扇形OAB=×6π×(18+9)=81π cm2,
∴纸杯的侧面积=S扇形OAB-S扇形OCD=81π-36π=45π cm2,
∵纸杯的底面积=π×=4π cm2,
∴纸杯的表面积=45π+4π=49π cm2.
19.解析 (1)设圆锥的母线长为l,底面圆半径为r,高为h,根据题意得3π=,∴l=3,∴πr×3=3π.解得r=1,∴h==2,故这个圆锥形筒的高为2.
(2)如图,画出这个圆锥的侧面展开图,连接BC、BD,则BD的长为蚂蚁爬行的最短路程.
由题意可知,∠BAC=120°÷2=60°,
∵AB=AC,
∴△ABC为等边三角形.
∵D为AC的中点,
∴BD⊥AC.
在Rt△ABD中,BD=AB·sin 60°=3×=.
故蚂蚁爬行的最短路程为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
