第8章 投影与识图素养综合检测试题(含解析)
文档属性
| 名称 | 第8章 投影与识图素养综合检测试题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 572.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024青岛版数学九年级下学期
第8章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
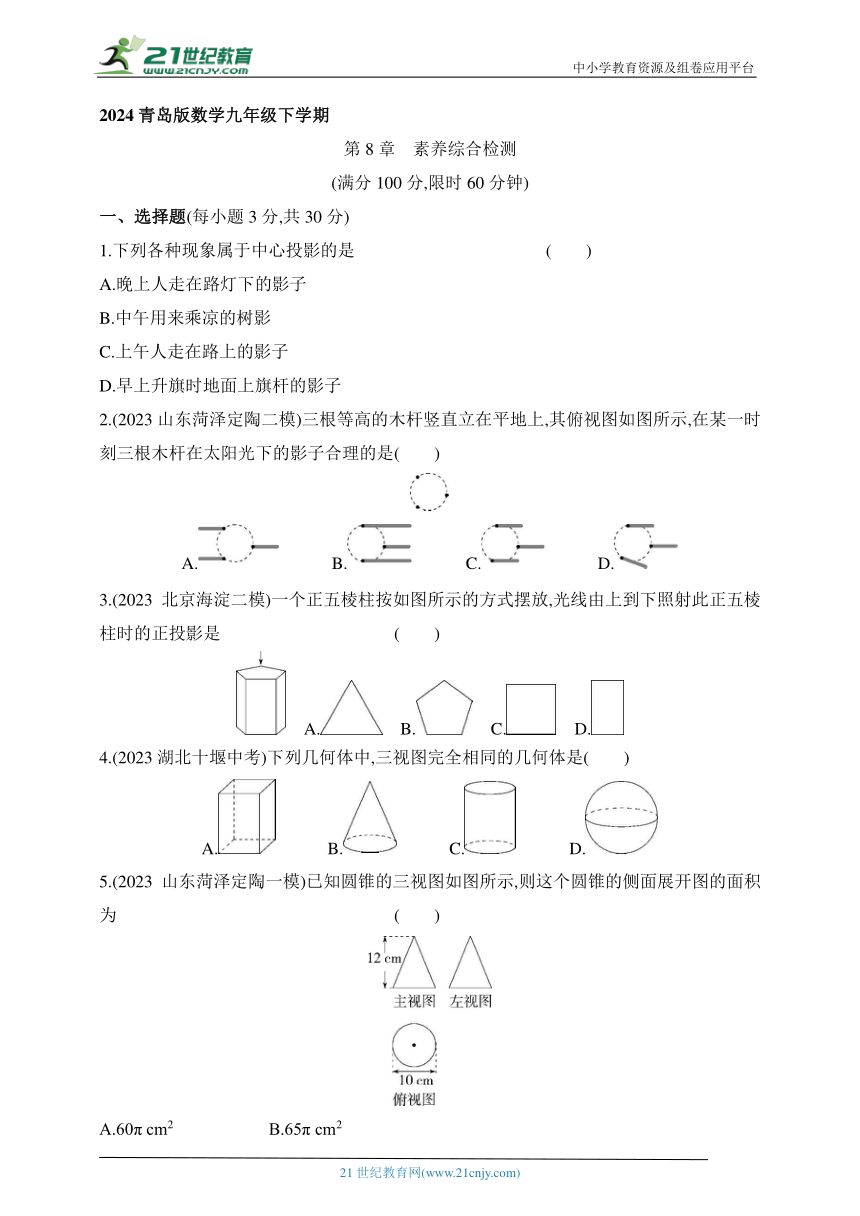
1.下列各种现象属于中心投影的是 ( )
A.晚上人走在路灯下的影子
B.中午用来乘凉的树影
C.上午人走在路上的影子
D.早上升旗时地面上旗杆的影子
2.(2023山东菏泽定陶二模)三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A. B. C. D.
3.(2023北京海淀二模)一个正五棱柱按如图所示的方式摆放,光线由上到下照射此正五棱柱时的正投影是 ( )
A. B. C. D.
4.(2023湖北十堰中考)下列几何体中,三视图完全相同的几何体是( )
A. B. C. D.
5.(2023山东菏泽定陶一模)已知圆锥的三视图如图所示,则这个圆锥的侧面展开图的面积为 ( )
A.60π cm2 B.65π cm2
C.120π cm2 D.130π cm2
6.(2023山东济南历城期末)如图,电灯P(看成一个点)在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=6 m,横杆AB与CD的距离是3 m,则P到AB的距离是 ( )
A. m B.1 m C. m D.3 m
7.(2023山东临朐一模)如图,在一个正方体的上底面中间位置挖一个长和宽均为6厘米、深为4厘米的长方体形状的洞,得到的几何体的三视图中既是轴对称图形又是中心对称图形的是 ( )
A.主视图 B.左视图 C.俯视图 D.不存在
8.【教材变式·P181综合练习T2】在一间屋子里的屋顶上挂着一盏白炽灯,在它的正下方有一个球,如图所示,下列说法错误的是 ( )
A.球在地面上的影子是圆
B.当球向上移动时,它的影子会增大
C.当球向下移动时,它的影子会减小
D.当球向上或向下移动时,它的影子大小不变
9.【新独家原创】如图所示的是由6个大小相同的小正方体堆砌而成的几何体,下列说法正确的是 ( )
A.取走①,主视图和左视图不变
B.取走②,俯视图和左视图不变
C.取走③,主视图和左视图不变
D.取走④,俯视图和左视图不变
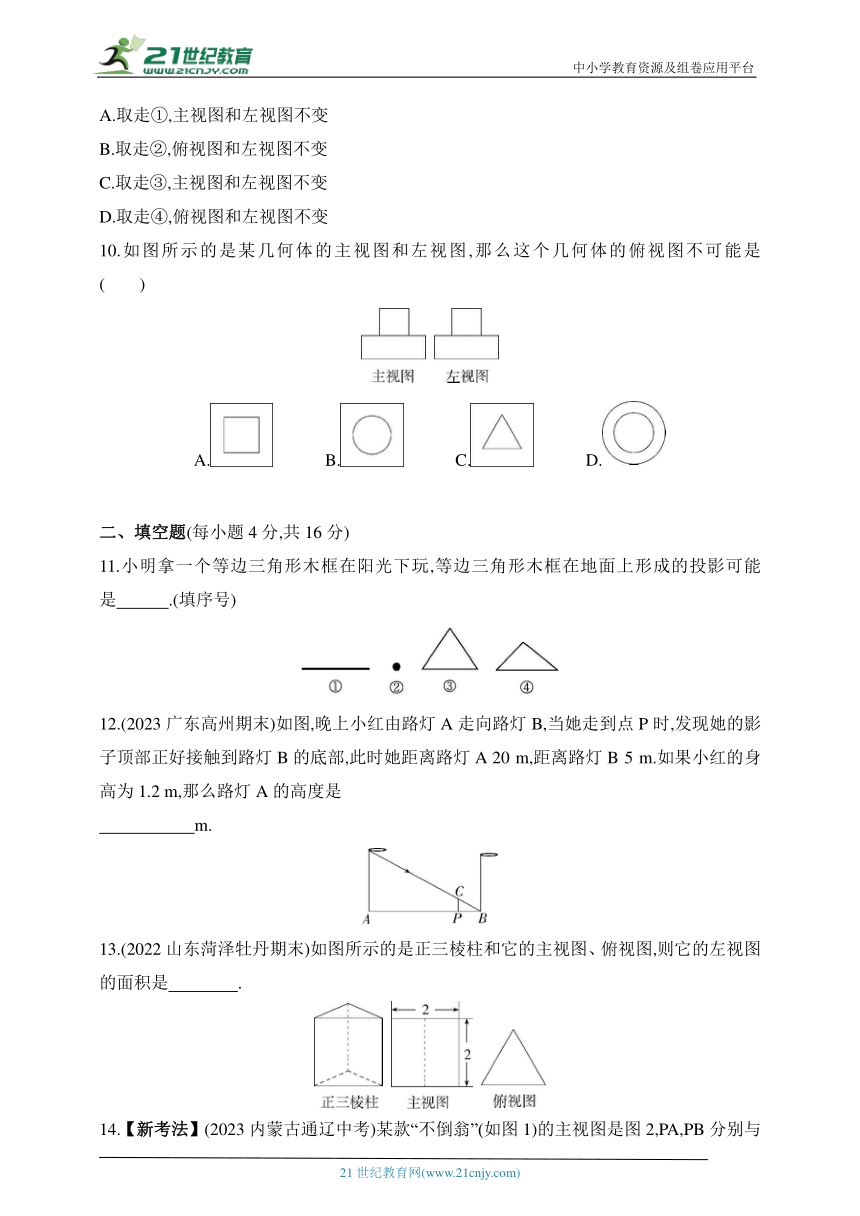
10.如图所示的是某几何体的主视图和左视图,那么这个几何体的俯视图不可能是 ( )
A. B. C. D.
二、填空题(每小题4分,共16分)
11.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上形成的投影可能是 .(填序号)
12.(2023广东高州期末)如图,晚上小红由路灯A走向路灯B,当她走到点P时,发现她的影子顶部正好接触到路灯B的底部,此时她距离路灯A 20 m,距离路灯B 5 m.如果小红的身高为1.2 m,那么路灯A的高度是
m.
13.(2022山东菏泽牡丹期末)如图所示的是正三棱柱和它的主视图、俯视图,则它的左视图的面积是 .
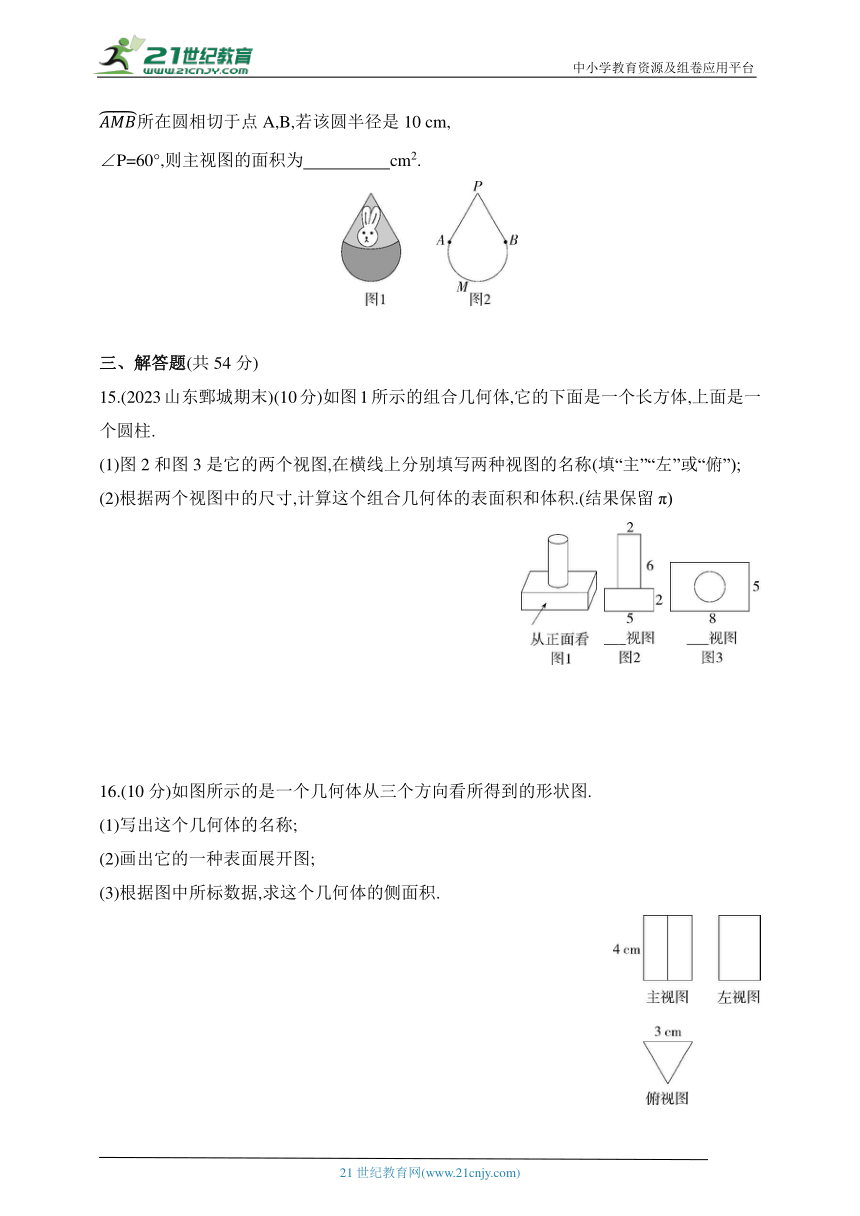
14.【新考法】(2023内蒙古通辽中考)某款“不倒翁”(如图1)的主视图是图2,PA,PB分别与所在圆相切于点A,B,若该圆半径是10 cm,
∠P=60°,则主视图的面积为 cm2.
三、解答题(共54分)
15.(2023山东鄄城期末)(10分)如图1所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图2和图3是它的两个视图,在横线上分别填写两种视图的名称(填“主”“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的表面积和体积.(结果保留π)
16.(10分)如图所示的是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)根据图中所标数据,求这个几何体的侧面积.
17.(10分)如图,身高为1.6 m的小王晚上在路灯下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走
20 m到M处,发现自己的影子的顶端刚好在点P处,继续向东走5 m到P处,此时影子的顶端在点Q处.
(1)找出路灯的位置;
(2)估计路灯的高,并求影长PQ.
18.(2023陕西乾县三模)(12分)某小组的项目式学习活动内容是测量某棵古树的高度AB,如图,在阳光下,某一时刻,古树AB的影子落在了地上和围墙上,落在地上的长度BD=21米,落在墙上的长度DE=1米,在古树的附近有一棵小树,同一时刻,小树的影长PN=1.8米,小树的高MN=1.2米.已知点N,P,B,D在一条水平线上,MN⊥ND,AB⊥BD,
ED⊥BD,请求出该古树的高度AB.
19.【跨学科·物理】(2023浙江仙居一模)(12分)如图1,点光源O射出光线沿直线传播,将胶片上的建筑物图片AB投影到与胶片平行的屏幕上,形成影像CD.已知AB=0.3 dm,胶片与屏幕的距离EF为定值,设点光源到胶片的距离OE的长为x dm,CD的长为y dm,当x=6时,y=4.3.
(1)求EF的长;
(2)求y关于x的函数解析式,在图2中画出图象,并写出至少一条该函数的性质;
(3)若要求CD的长不小于3 dm,求OE长的取值范围.
答案全解全析
1.A 选项A是路灯下的影子,是中心投影,选项B、C、D都是在太阳光下的影子,是平行投影.故选A.
2.C 在某一时刻三根木杆在太阳光下的影子的方向一致,影子的长度相同,故正确的选项是C.
3.B 光线由上向下照射此正五棱柱时的正投影是正五边形.故选B.
4.D A.长方体的主视图、左视图和俯视图均为矩形,但三个矩形不完全相同,故不符合题意;B.圆锥的主视图和左视图是完全相同的等腰三角形,俯视图是带圆心的圆,故不符合题意;C.圆柱的主视图和左视图是完全相同的矩形,俯视图是圆,故不符合题意;D.球的主视图、左视图和俯视图是完全相同的圆,故符合题意.故选D.
5.B 根据三视图得到圆锥的底面圆的直径为10 cm,即圆锥底面圆的半径为5 cm,圆锥的高为12 cm,所以圆锥的母线长==13 cm,所以这个圆锥的侧面积=π×5×13=65π(cm2),即这个圆锥的侧面展开图的面积是65π cm2.故选B.
6.A 如图,过点P作PF⊥CD于F,交AB于点E.
∵AB∥CD,∴△PAB∽△PCD,
∴=,∴=,
∴PE= m.
∴P到AB的距离为 m,故选A.
7.C 画出得到的几何体的三视图如图所示:
既是轴对称图形又是中心对称图形的是俯视图.故选C.
8.D 因为光源在球的正上方,所以球在地面上的影子是圆,A选项说法正确;当球向上移动时,靠近光源,影子变大,当球向下移动时,远离光源,影子变小,B、C选项说法正确,D选项说法错误.故选D.
9.B 取走①,主视图不变,但左视图变化了,A错误;取走②,俯视图和左视图都不变,B正确;取走③,主视图变化了,左视图不变,C错误;取走④,俯视图变化了,左视图不变,D错误.故选B.
10.C 若该几何体是由一个正方体和一个底面是正方形的长方体组成的,则俯视图可能是A;若该几何体是由一个底面是正方形的长方体和一个圆柱组成的,则俯视图可能是B;若该几何体是由一个三棱柱和一个底面是正方形的长方体组成的,则俯视图是C,但主视图上方正方形中间应该有一条竖直的虚线,故原几何体的俯视图不可能是C;若该几何体是由两个圆柱组成的,则俯视图可能是D.故选C.
11.答案 ①③④
解析 当等边三角形木框与阳光平行时,投影是①;当等边三角形木框与阳光垂直时,投影是③;当等边三角形木框与阳光有一定角度时,投影可能是④.
12.答案 6
解析 设路灯A的高度为x m,路灯A的顶部为D,
易知△BAD∽△BPC,∴=,
即=,解得x=6,∴路灯A的高度是6 m.
13.答案 2
解析 如图,过点B作BD⊥AC于点D,
俯视图
由题意得AB=AC=BC=2,∴AD=1,∴BD=,
易知左视图为矩形,矩形的长为2,宽为,
∴左视图的面积为2×=2.
14.答案
解析 本题考查不规则立体图形主视图的面积,解题时应注意转化为规则图形的面积进行计算.
如图,设圆心为O,连接OA,OB,OP.
∵PA,PB与所在圆相切,
∴∠OAP=∠OBP=90°,PA=PB,
∵OA=OB,∴△OAP≌△OBP,
∴∠APO=∠BPO=×60°=30°.
∴PA=PB=OA=10(cm),
∴S四边形AOBP=2S△AOP=2××10×10=100(cm2),
∵∠AOB=360°-90°-90°-60°=120°,
∴的度数为360°-120°=240°,
∴==(cm2).
∴主视图的面积为cm2.
15.解析 (1)题图2为左视图,题图3为俯视图.
(2)表面积为(8×5+8×2+5×2)×2+2π×6=132+12π,
体积为2×5×8+π×(2÷2)2×6=80+π×1×6=80+6π.
16.解析 (1)这个几何体的名称是三棱柱.
(2)表面展开图如图所示(答案不唯一):
(3)3×4×3=36(cm2),
∴这个几何体的侧面积为36 cm2.
17.解析 (1)如图,点O为路灯的位置.
(2)作OA⊥MQ,垂足为A,如图,AM=20 m,MP=5 m,MN=PB=1.6 m,
∵MN∥OA,∴△PMN∽△PAO,
∴=,即=,∴OA=8 m,
∵PB∥OA,∴△QPB∽△QAO,
∴=,即=,∴PQ= m.
答:路灯的高为8 m,影长PQ为 m.
18.解析 连接AE,MP,延长AE交直线BD于点Q,过点E作EF⊥AB于点F,
由题意可得,∠MPN=∠AQB,EF=BD=21米,BF=DE=1米,
∵AB⊥ND,EF⊥AB,∴FE∥BQ,
∴∠MPN=∠AQB=∠AEF,
∵∠MNP=∠AFE=90°,∴△MNP∽△AFE,
∴=,∴=,
∴AF=14米,∴AB=AF+BF=14+1=15米,
∴该古树的高度AB为15米.
19.解析 (1)∵AB∥CD,∴△OAB∽△OCD,
∴=,∴=,∴EF=80 dm.
答:EF的长为80 dm.
(2)由(1)得,=,
∴=,∴y=0.3+,
画出函数图象如图所示:
性质:当x>0时,y随x的增大而减小(答案不唯一).
(3)令y=3,得0.3+=3,解得x=.
由图象可知,当y≥3时,0∴OE长的取值范围为021世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学九年级下学期
第8章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.下列各种现象属于中心投影的是 ( )
A.晚上人走在路灯下的影子
B.中午用来乘凉的树影
C.上午人走在路上的影子
D.早上升旗时地面上旗杆的影子
2.(2023山东菏泽定陶二模)三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A. B. C. D.
3.(2023北京海淀二模)一个正五棱柱按如图所示的方式摆放,光线由上到下照射此正五棱柱时的正投影是 ( )
A. B. C. D.
4.(2023湖北十堰中考)下列几何体中,三视图完全相同的几何体是( )
A. B. C. D.
5.(2023山东菏泽定陶一模)已知圆锥的三视图如图所示,则这个圆锥的侧面展开图的面积为 ( )
A.60π cm2 B.65π cm2
C.120π cm2 D.130π cm2
6.(2023山东济南历城期末)如图,电灯P(看成一个点)在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=6 m,横杆AB与CD的距离是3 m,则P到AB的距离是 ( )
A. m B.1 m C. m D.3 m
7.(2023山东临朐一模)如图,在一个正方体的上底面中间位置挖一个长和宽均为6厘米、深为4厘米的长方体形状的洞,得到的几何体的三视图中既是轴对称图形又是中心对称图形的是 ( )
A.主视图 B.左视图 C.俯视图 D.不存在
8.【教材变式·P181综合练习T2】在一间屋子里的屋顶上挂着一盏白炽灯,在它的正下方有一个球,如图所示,下列说法错误的是 ( )
A.球在地面上的影子是圆
B.当球向上移动时,它的影子会增大
C.当球向下移动时,它的影子会减小
D.当球向上或向下移动时,它的影子大小不变
9.【新独家原创】如图所示的是由6个大小相同的小正方体堆砌而成的几何体,下列说法正确的是 ( )
A.取走①,主视图和左视图不变
B.取走②,俯视图和左视图不变
C.取走③,主视图和左视图不变
D.取走④,俯视图和左视图不变
10.如图所示的是某几何体的主视图和左视图,那么这个几何体的俯视图不可能是 ( )
A. B. C. D.
二、填空题(每小题4分,共16分)
11.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上形成的投影可能是 .(填序号)
12.(2023广东高州期末)如图,晚上小红由路灯A走向路灯B,当她走到点P时,发现她的影子顶部正好接触到路灯B的底部,此时她距离路灯A 20 m,距离路灯B 5 m.如果小红的身高为1.2 m,那么路灯A的高度是
m.
13.(2022山东菏泽牡丹期末)如图所示的是正三棱柱和它的主视图、俯视图,则它的左视图的面积是 .
14.【新考法】(2023内蒙古通辽中考)某款“不倒翁”(如图1)的主视图是图2,PA,PB分别与所在圆相切于点A,B,若该圆半径是10 cm,
∠P=60°,则主视图的面积为 cm2.
三、解答题(共54分)
15.(2023山东鄄城期末)(10分)如图1所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图2和图3是它的两个视图,在横线上分别填写两种视图的名称(填“主”“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的表面积和体积.(结果保留π)
16.(10分)如图所示的是一个几何体从三个方向看所得到的形状图.
(1)写出这个几何体的名称;
(2)画出它的一种表面展开图;
(3)根据图中所标数据,求这个几何体的侧面积.
17.(10分)如图,身高为1.6 m的小王晚上在路灯下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走
20 m到M处,发现自己的影子的顶端刚好在点P处,继续向东走5 m到P处,此时影子的顶端在点Q处.
(1)找出路灯的位置;
(2)估计路灯的高,并求影长PQ.
18.(2023陕西乾县三模)(12分)某小组的项目式学习活动内容是测量某棵古树的高度AB,如图,在阳光下,某一时刻,古树AB的影子落在了地上和围墙上,落在地上的长度BD=21米,落在墙上的长度DE=1米,在古树的附近有一棵小树,同一时刻,小树的影长PN=1.8米,小树的高MN=1.2米.已知点N,P,B,D在一条水平线上,MN⊥ND,AB⊥BD,
ED⊥BD,请求出该古树的高度AB.
19.【跨学科·物理】(2023浙江仙居一模)(12分)如图1,点光源O射出光线沿直线传播,将胶片上的建筑物图片AB投影到与胶片平行的屏幕上,形成影像CD.已知AB=0.3 dm,胶片与屏幕的距离EF为定值,设点光源到胶片的距离OE的长为x dm,CD的长为y dm,当x=6时,y=4.3.
(1)求EF的长;
(2)求y关于x的函数解析式,在图2中画出图象,并写出至少一条该函数的性质;
(3)若要求CD的长不小于3 dm,求OE长的取值范围.
答案全解全析
1.A 选项A是路灯下的影子,是中心投影,选项B、C、D都是在太阳光下的影子,是平行投影.故选A.
2.C 在某一时刻三根木杆在太阳光下的影子的方向一致,影子的长度相同,故正确的选项是C.
3.B 光线由上向下照射此正五棱柱时的正投影是正五边形.故选B.
4.D A.长方体的主视图、左视图和俯视图均为矩形,但三个矩形不完全相同,故不符合题意;B.圆锥的主视图和左视图是完全相同的等腰三角形,俯视图是带圆心的圆,故不符合题意;C.圆柱的主视图和左视图是完全相同的矩形,俯视图是圆,故不符合题意;D.球的主视图、左视图和俯视图是完全相同的圆,故符合题意.故选D.
5.B 根据三视图得到圆锥的底面圆的直径为10 cm,即圆锥底面圆的半径为5 cm,圆锥的高为12 cm,所以圆锥的母线长==13 cm,所以这个圆锥的侧面积=π×5×13=65π(cm2),即这个圆锥的侧面展开图的面积是65π cm2.故选B.
6.A 如图,过点P作PF⊥CD于F,交AB于点E.
∵AB∥CD,∴△PAB∽△PCD,
∴=,∴=,
∴PE= m.
∴P到AB的距离为 m,故选A.
7.C 画出得到的几何体的三视图如图所示:
既是轴对称图形又是中心对称图形的是俯视图.故选C.
8.D 因为光源在球的正上方,所以球在地面上的影子是圆,A选项说法正确;当球向上移动时,靠近光源,影子变大,当球向下移动时,远离光源,影子变小,B、C选项说法正确,D选项说法错误.故选D.
9.B 取走①,主视图不变,但左视图变化了,A错误;取走②,俯视图和左视图都不变,B正确;取走③,主视图变化了,左视图不变,C错误;取走④,俯视图变化了,左视图不变,D错误.故选B.
10.C 若该几何体是由一个正方体和一个底面是正方形的长方体组成的,则俯视图可能是A;若该几何体是由一个底面是正方形的长方体和一个圆柱组成的,则俯视图可能是B;若该几何体是由一个三棱柱和一个底面是正方形的长方体组成的,则俯视图是C,但主视图上方正方形中间应该有一条竖直的虚线,故原几何体的俯视图不可能是C;若该几何体是由两个圆柱组成的,则俯视图可能是D.故选C.
11.答案 ①③④
解析 当等边三角形木框与阳光平行时,投影是①;当等边三角形木框与阳光垂直时,投影是③;当等边三角形木框与阳光有一定角度时,投影可能是④.
12.答案 6
解析 设路灯A的高度为x m,路灯A的顶部为D,
易知△BAD∽△BPC,∴=,
即=,解得x=6,∴路灯A的高度是6 m.
13.答案 2
解析 如图,过点B作BD⊥AC于点D,
俯视图
由题意得AB=AC=BC=2,∴AD=1,∴BD=,
易知左视图为矩形,矩形的长为2,宽为,
∴左视图的面积为2×=2.
14.答案
解析 本题考查不规则立体图形主视图的面积,解题时应注意转化为规则图形的面积进行计算.
如图,设圆心为O,连接OA,OB,OP.
∵PA,PB与所在圆相切,
∴∠OAP=∠OBP=90°,PA=PB,
∵OA=OB,∴△OAP≌△OBP,
∴∠APO=∠BPO=×60°=30°.
∴PA=PB=OA=10(cm),
∴S四边形AOBP=2S△AOP=2××10×10=100(cm2),
∵∠AOB=360°-90°-90°-60°=120°,
∴的度数为360°-120°=240°,
∴==(cm2).
∴主视图的面积为cm2.
15.解析 (1)题图2为左视图,题图3为俯视图.
(2)表面积为(8×5+8×2+5×2)×2+2π×6=132+12π,
体积为2×5×8+π×(2÷2)2×6=80+π×1×6=80+6π.
16.解析 (1)这个几何体的名称是三棱柱.
(2)表面展开图如图所示(答案不唯一):
(3)3×4×3=36(cm2),
∴这个几何体的侧面积为36 cm2.
17.解析 (1)如图,点O为路灯的位置.
(2)作OA⊥MQ,垂足为A,如图,AM=20 m,MP=5 m,MN=PB=1.6 m,
∵MN∥OA,∴△PMN∽△PAO,
∴=,即=,∴OA=8 m,
∵PB∥OA,∴△QPB∽△QAO,
∴=,即=,∴PQ= m.
答:路灯的高为8 m,影长PQ为 m.
18.解析 连接AE,MP,延长AE交直线BD于点Q,过点E作EF⊥AB于点F,
由题意可得,∠MPN=∠AQB,EF=BD=21米,BF=DE=1米,
∵AB⊥ND,EF⊥AB,∴FE∥BQ,
∴∠MPN=∠AQB=∠AEF,
∵∠MNP=∠AFE=90°,∴△MNP∽△AFE,
∴=,∴=,
∴AF=14米,∴AB=AF+BF=14+1=15米,
∴该古树的高度AB为15米.
19.解析 (1)∵AB∥CD,∴△OAB∽△OCD,
∴=,∴=,∴EF=80 dm.
答:EF的长为80 dm.
(2)由(1)得,=,
∴=,∴y=0.3+,
画出函数图象如图所示:
性质:当x>0时,y随x的增大而减小(答案不唯一).
(3)令y=3,得0.3+=3,解得x=.
由图象可知,当y≥3时,0
21世纪教育网(www.21cnjy.com)
