27.1 图形的相似课时练(含解析)
文档属性
| 名称 | 27.1 图形的相似课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 399.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 21:37:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十七章 相似
27.1 图形的相似
基础过关全练
知识点1 相似图形
1.【教材变式·P25T2】请认真观察如图所示的各组中的两个图形,哪些是相似图形 哪些不是相似图形
知识点2 比例线段
2.(2023甘肃庆阳中考)若,则ab=( )
A.6 B.
3.(2023山西运城夏县月考)下列长度的四组线段中,成比例的一组是( )
A.1,1.5,3,3.5 B.
C.1, D.4,5,6,7
4.【跨学科·地理】【教材变式·P27练习T1】在比例尺为1∶100 000的地图上,甲、乙两地图距是2 cm,则它们的实际距离为( )
A.100 km B.2 000 m C.10 km D.20 km
5.(2023广东深圳翠园教育集团期中)已知且b+d≠0,下列各式正确的是( )
A.3c=4d B.
6.(2023江苏盐城阜宁期末)已知a,b,c,d是成比例的线段,其中a=3 cm,b=2 cm,d=6 cm,则c= .
知识点3 相似多边形及其性质
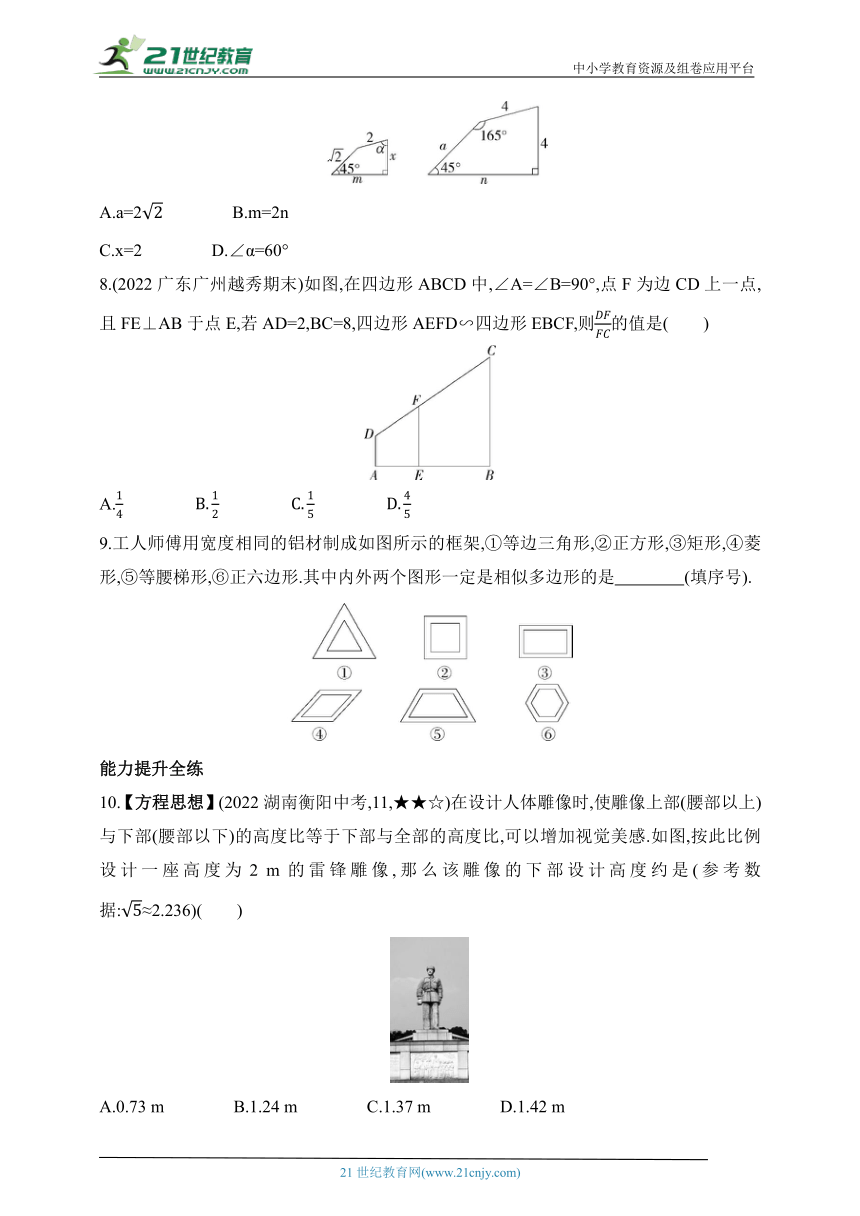
7.(2023四川成都锦江期末)如图所示的两个四边形相似,则下列结论不正确的是( )
A.a=2 B.m=2n
C.x=2 D.∠α=60°
8.(2022广东广州越秀期末)如图,在四边形ABCD中,∠A=∠B=90°,点F为边CD上一点,且FE⊥AB于点E,若AD=2,BC=8,四边形AEFD∽四边形EBCF,则的值是( )
A.
9.工人师傅用宽度相同的铝材制成如图所示的框架,①等边三角形,②正方形,③矩形,④菱形,⑤等腰梯形,⑥正六边形.其中内外两个图形一定是相似多边形的是 (填序号).
能力提升全练
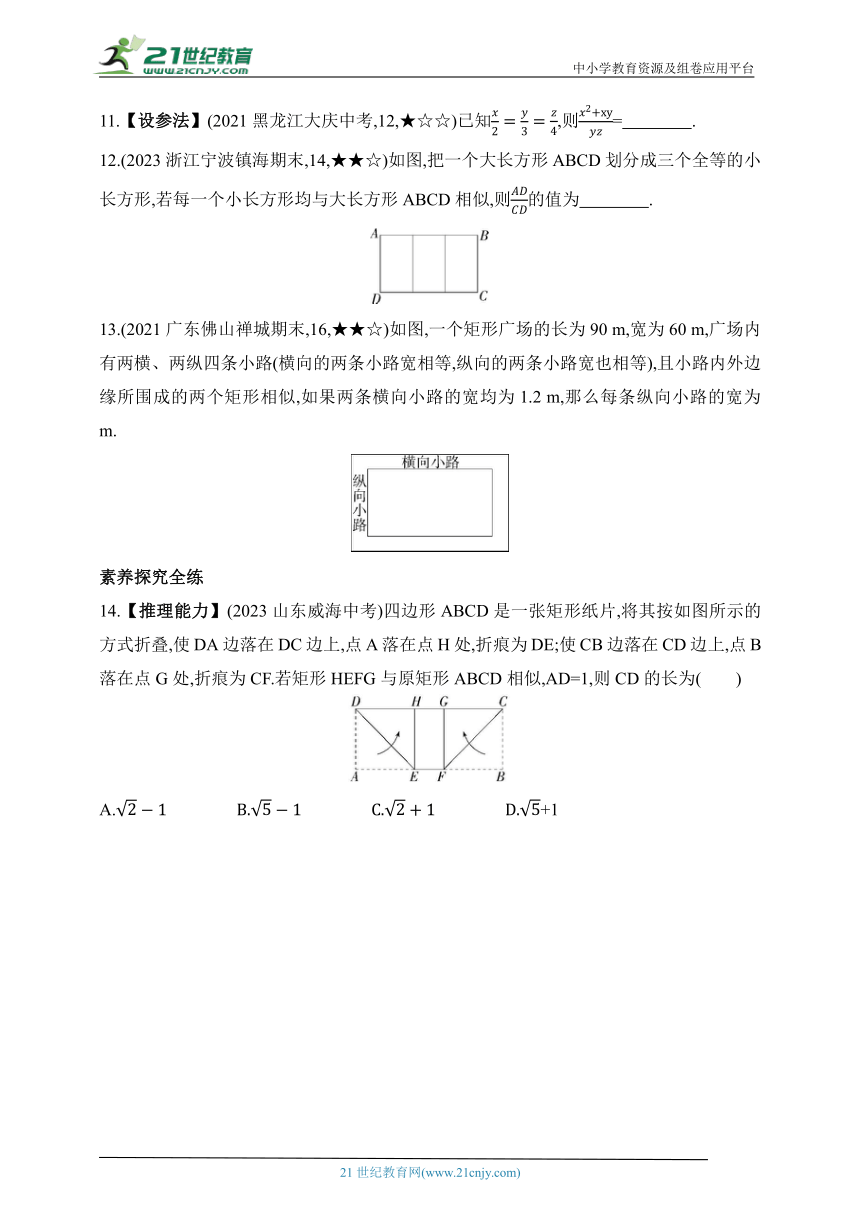
10.【方程思想】(2022湖南衡阳中考,11,★★☆)在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2 m的雷锋雕像,那么该雕像的下部设计高度约是(参考数据:≈2.236)( )
A.0.73 m B.1.24 m C.1.37 m D.1.42 m
11.【设参法】(2021黑龙江大庆中考,12,★☆☆)已知,则= .
12.(2023浙江宁波镇海期末,14,★★☆)如图,把一个大长方形ABCD划分成三个全等的小长方形,若每一个小长方形均与大长方形ABCD相似,则的值为 .
13.(2021广东佛山禅城期末,16,★★☆)如图,一个矩形广场的长为90 m,宽为60 m,广场内有两横、两纵四条小路(横向的两条小路宽相等,纵向的两条小路宽也相等),且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2 m,那么每条纵向小路的宽为 m.
素养探究全练
14.【推理能力】(2023山东威海中考)四边形ABCD是一张矩形纸片,将其按如图所示的方式折叠,使DA边落在DC边上,点A落在点H处,折痕为DE;使CB边落在CD边上,点B落在点G处,折痕为CF.若矩形HEFG与原矩形ABCD相似,AD=1,则CD的长为( )
A.+1
答案全解全析
基础过关全练
1.解析 ③⑤都是相似图形,①②④⑥都不是相似图形.
2.A ∵,∴ab=6.故选A.
3.C 选项A,∵1×3.5≠1.5×3,∴四条线段不成比例;选项B,∵≠3×3,∴四条线段不成比例;选项C,∵1××3,∴四条线段成比例;选项D,∵4×7≠5×6,∴四条线段不成比例.故选C.
4.B 设甲、乙两地实际距离为x cm,由题意,得2∶x=1∶100 000,∴x=200 000,200 000 cm=2 000 m.故选B.
5.B ∵,∴4c=3d,所以A选项不符合题意;∵且b+d≠0,∴,所以B选项符合题意;∵,所以C选项不符合题意;∵,所以D选项不符合题意.故选B.
6.9 cm
解析 ∵a,b,c,d是成比例的线段,∴ad=bc,将a=3 cm,b=2 cm,d=6 cm代入,得3×6=2c,解得c=9(cm).
7.B ∵两个四边形相似,相似比为2∶4=1∶2,∴∶a=x∶4=m∶n=1∶2,得a=2,x=2,2m=n,又∵∠α=360°-45°-90°-165°=60°,∴只有选项B符合题意.故选B.
8.B ∵四边形AEFD∽四边形EBCF,∴.∵AD=2,BC=8,∴EF2=2×8=16,∴EF=4.∵四边形AEFD∽四边形EBCF,∴.故选B.
9.①②④⑥
解析 由题意得①②④⑥中的两个图形各角分别相等,各边成比例,两个图形相似;③⑤中的两个图形各角分别相等,各边不一定成比例,不一定相似.
能力提升全练
10.B 设下部的高度为x m,则上部的高度是(2-x)m,∵雕像上部(腰部以上)与下部(腰部以下)的高度比等于下部与全部的高度比,∴,解得x=-1或x=--1(舍去),∴x=-1≈1.24.故选B.
11.
解析 设=k(k≠0),则x=2k,y=3k,z=4k,∴.
方法解读 设参法:当题目中出现比例、连等时,设比值等于一个参数(如k),然后把比中的未知数用参数表示,最后在运算时约去参数从而解决问题.
12.
解析 如图,由题意,得DE=DC,矩形DEFA∽矩形ADCB,∴.
13.1.8
解析 设每条纵向小路的宽为x m,
∵小路内外边缘所围成的两个矩形相似,
∴,
解得x=1.8或x=25.8(不合实际,舍去).
故每条纵向小路的宽为1.8 m.
素养探究全练
C 设HG=x,∵四边形ABCD是矩形,
∴∠A=∠ADH=90°,AD=BC=1.
由折叠得GC=BC=1,∠A=∠DHE=90°,AD=DH=1,
∴四边形ADHE是正方形,∴AD=HE=1.
∵矩形HEFG与原矩形ABCD相似,∴,
解得x=-1或x=--1(舍去),∴DC=2+x=+1.故选C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十七章 相似
27.1 图形的相似
基础过关全练
知识点1 相似图形
1.【教材变式·P25T2】请认真观察如图所示的各组中的两个图形,哪些是相似图形 哪些不是相似图形
知识点2 比例线段
2.(2023甘肃庆阳中考)若,则ab=( )
A.6 B.
3.(2023山西运城夏县月考)下列长度的四组线段中,成比例的一组是( )
A.1,1.5,3,3.5 B.
C.1, D.4,5,6,7
4.【跨学科·地理】【教材变式·P27练习T1】在比例尺为1∶100 000的地图上,甲、乙两地图距是2 cm,则它们的实际距离为( )
A.100 km B.2 000 m C.10 km D.20 km
5.(2023广东深圳翠园教育集团期中)已知且b+d≠0,下列各式正确的是( )
A.3c=4d B.
6.(2023江苏盐城阜宁期末)已知a,b,c,d是成比例的线段,其中a=3 cm,b=2 cm,d=6 cm,则c= .
知识点3 相似多边形及其性质
7.(2023四川成都锦江期末)如图所示的两个四边形相似,则下列结论不正确的是( )
A.a=2 B.m=2n
C.x=2 D.∠α=60°
8.(2022广东广州越秀期末)如图,在四边形ABCD中,∠A=∠B=90°,点F为边CD上一点,且FE⊥AB于点E,若AD=2,BC=8,四边形AEFD∽四边形EBCF,则的值是( )
A.
9.工人师傅用宽度相同的铝材制成如图所示的框架,①等边三角形,②正方形,③矩形,④菱形,⑤等腰梯形,⑥正六边形.其中内外两个图形一定是相似多边形的是 (填序号).
能力提升全练
10.【方程思想】(2022湖南衡阳中考,11,★★☆)在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2 m的雷锋雕像,那么该雕像的下部设计高度约是(参考数据:≈2.236)( )
A.0.73 m B.1.24 m C.1.37 m D.1.42 m
11.【设参法】(2021黑龙江大庆中考,12,★☆☆)已知,则= .
12.(2023浙江宁波镇海期末,14,★★☆)如图,把一个大长方形ABCD划分成三个全等的小长方形,若每一个小长方形均与大长方形ABCD相似,则的值为 .
13.(2021广东佛山禅城期末,16,★★☆)如图,一个矩形广场的长为90 m,宽为60 m,广场内有两横、两纵四条小路(横向的两条小路宽相等,纵向的两条小路宽也相等),且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2 m,那么每条纵向小路的宽为 m.
素养探究全练
14.【推理能力】(2023山东威海中考)四边形ABCD是一张矩形纸片,将其按如图所示的方式折叠,使DA边落在DC边上,点A落在点H处,折痕为DE;使CB边落在CD边上,点B落在点G处,折痕为CF.若矩形HEFG与原矩形ABCD相似,AD=1,则CD的长为( )
A.+1
答案全解全析
基础过关全练
1.解析 ③⑤都是相似图形,①②④⑥都不是相似图形.
2.A ∵,∴ab=6.故选A.
3.C 选项A,∵1×3.5≠1.5×3,∴四条线段不成比例;选项B,∵≠3×3,∴四条线段不成比例;选项C,∵1××3,∴四条线段成比例;选项D,∵4×7≠5×6,∴四条线段不成比例.故选C.
4.B 设甲、乙两地实际距离为x cm,由题意,得2∶x=1∶100 000,∴x=200 000,200 000 cm=2 000 m.故选B.
5.B ∵,∴4c=3d,所以A选项不符合题意;∵且b+d≠0,∴,所以B选项符合题意;∵,所以C选项不符合题意;∵,所以D选项不符合题意.故选B.
6.9 cm
解析 ∵a,b,c,d是成比例的线段,∴ad=bc,将a=3 cm,b=2 cm,d=6 cm代入,得3×6=2c,解得c=9(cm).
7.B ∵两个四边形相似,相似比为2∶4=1∶2,∴∶a=x∶4=m∶n=1∶2,得a=2,x=2,2m=n,又∵∠α=360°-45°-90°-165°=60°,∴只有选项B符合题意.故选B.
8.B ∵四边形AEFD∽四边形EBCF,∴.∵AD=2,BC=8,∴EF2=2×8=16,∴EF=4.∵四边形AEFD∽四边形EBCF,∴.故选B.
9.①②④⑥
解析 由题意得①②④⑥中的两个图形各角分别相等,各边成比例,两个图形相似;③⑤中的两个图形各角分别相等,各边不一定成比例,不一定相似.
能力提升全练
10.B 设下部的高度为x m,则上部的高度是(2-x)m,∵雕像上部(腰部以上)与下部(腰部以下)的高度比等于下部与全部的高度比,∴,解得x=-1或x=--1(舍去),∴x=-1≈1.24.故选B.
11.
解析 设=k(k≠0),则x=2k,y=3k,z=4k,∴.
方法解读 设参法:当题目中出现比例、连等时,设比值等于一个参数(如k),然后把比中的未知数用参数表示,最后在运算时约去参数从而解决问题.
12.
解析 如图,由题意,得DE=DC,矩形DEFA∽矩形ADCB,∴.
13.1.8
解析 设每条纵向小路的宽为x m,
∵小路内外边缘所围成的两个矩形相似,
∴,
解得x=1.8或x=25.8(不合实际,舍去).
故每条纵向小路的宽为1.8 m.
素养探究全练
C 设HG=x,∵四边形ABCD是矩形,
∴∠A=∠ADH=90°,AD=BC=1.
由折叠得GC=BC=1,∠A=∠DHE=90°,AD=DH=1,
∴四边形ADHE是正方形,∴AD=HE=1.
∵矩形HEFG与原矩形ABCD相似,∴,
解得x=-1或x=--1(舍去),∴DC=2+x=+1.故选C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
