27.2.1.2 相似三角形的判定(1)课时练(含解析)
文档属性
| 名称 | 27.2.1.2 相似三角形的判定(1)课时练(含解析) | 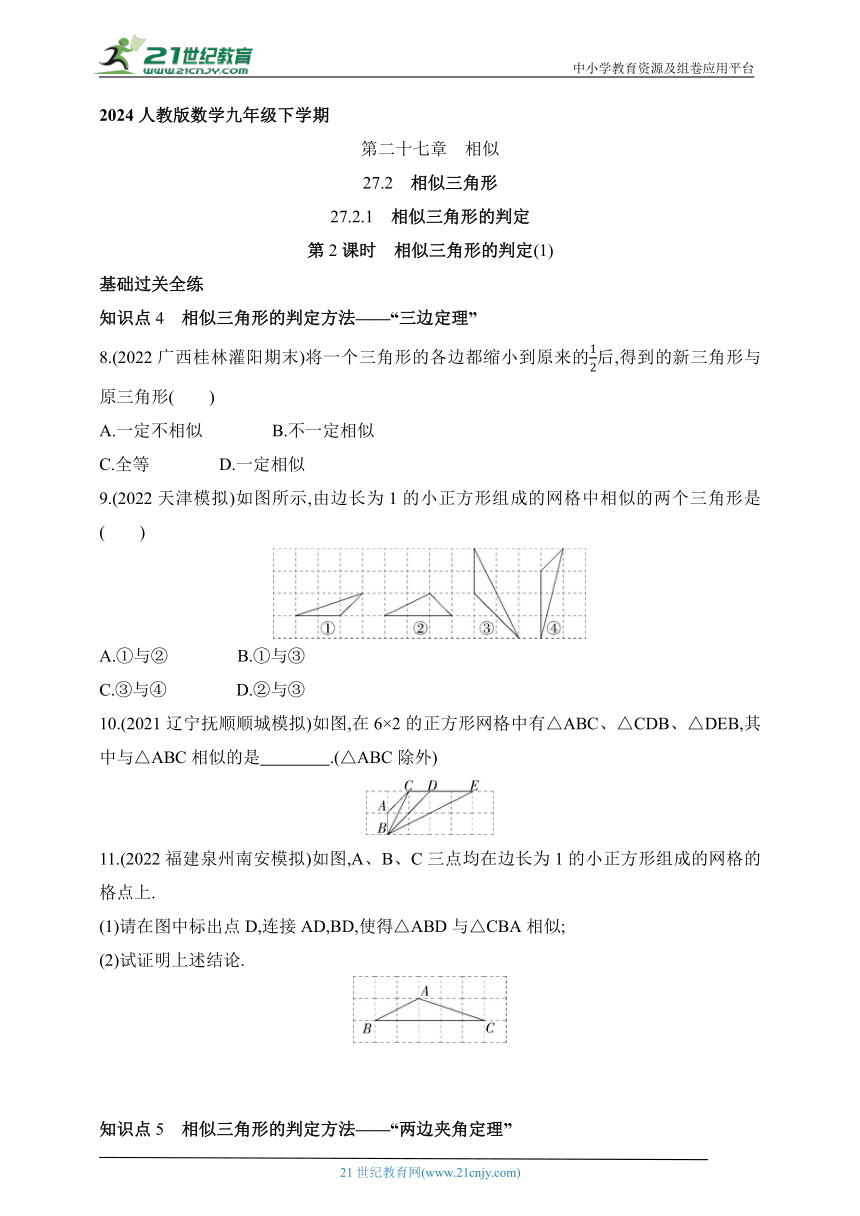 | |
| 格式 | docx | ||
| 文件大小 | 380.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 21:39:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十七章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第2课时 相似三角形的判定(1)
基础过关全练
知识点4 相似三角形的判定方法——“三边定理”
8.(2022广西桂林灌阳期末)将一个三角形的各边都缩小到原来的后,得到的新三角形与原三角形( )
A.一定不相似 B.不一定相似
C.全等 D.一定相似
9.(2022天津模拟)如图所示,由边长为1的小正方形组成的网格中相似的两个三角形是( )
A.①与② B.①与③
C.③与④ D.②与③
10.(2021辽宁抚顺顺城模拟)如图,在6×2的正方形网格中有△ABC、△CDB、△DEB,其中与△ABC相似的是 .(△ABC除外)
11.(2022福建泉州南安模拟)如图,A、B、C三点均在边长为1的小正方形组成的网格的格点上.
(1)请在图中标出点D,连接AD,BD,使得△ABD与△CBA相似;
(2)试证明上述结论.
知识点5 相似三角形的判定方法——“两边夹角定理”
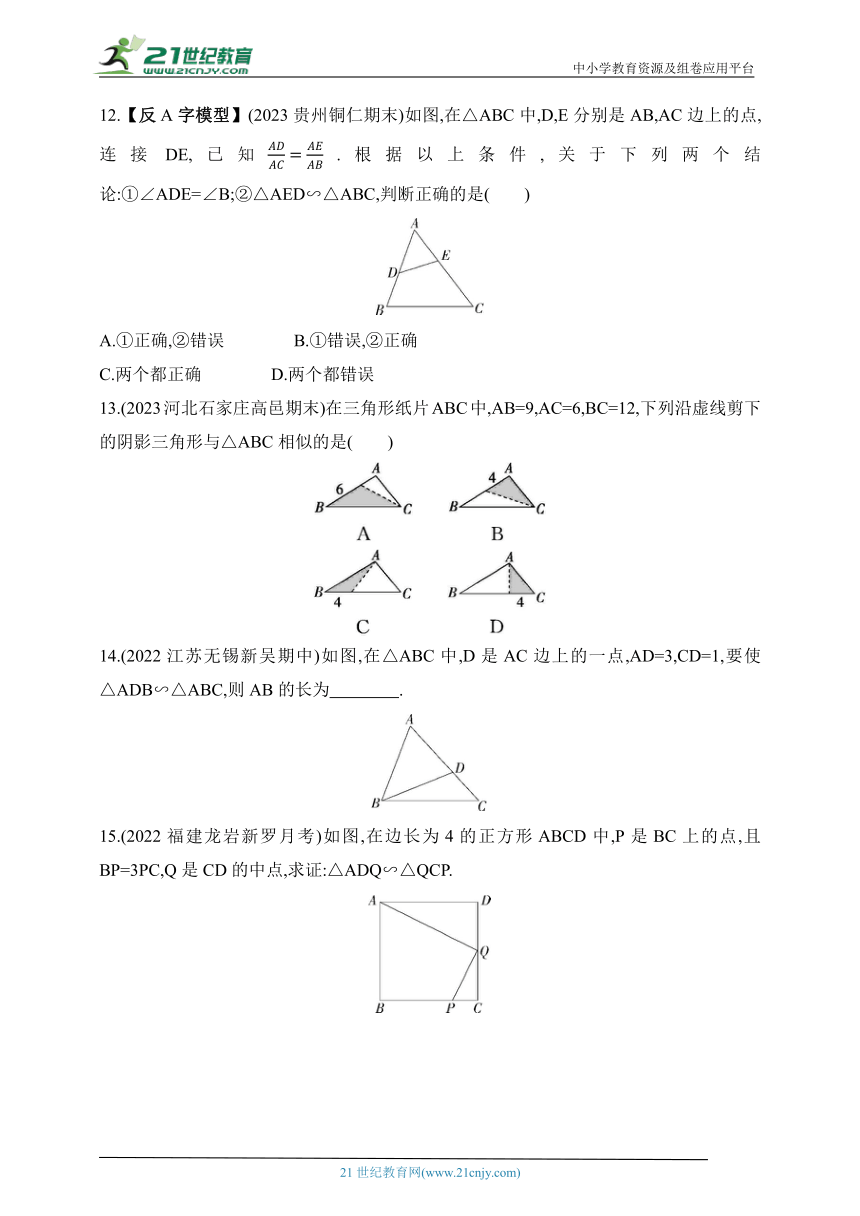
12.【反A字模型】(2023贵州铜仁期末)如图,在△ABC中,D,E分别是AB,AC边上的点,连接DE,已知.根据以上条件,关于下列两个结论:①∠ADE=∠B;②△AED∽△ABC,判断正确的是( )
A.①正确,②错误 B.①错误,②正确
C.两个都正确 D.两个都错误
13.(2023河北石家庄高邑期末)在三角形纸片ABC中,AB=9,AC=6,BC=12,下列沿虚线剪下的阴影三角形与△ABC相似的是( )
14.(2022江苏无锡新吴期中)如图,在△ABC中,D是AC边上的一点,AD=3,CD=1,要使△ADB∽△ABC,则AB的长为 .
15.(2022福建龙岩新罗月考)如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
答案全解全析
基础过关全练
8.D ∵将一个三角形的各边都缩小到原来的,∴新三角形的各边与原三角形的对应边的比值都为,∴新三角形与原三角形相似.故选D.
9.B 图形①的三边长分别为;图形②的三边长分别为3,;图形③的三边长分别为2,2;图形④的三边长分别为,∴①与③相似.故选B.
10.△DEB
解析 设小正方形的边长为1,则△ABC的三边长分别为AB=1,AC=;△CDB的三边长分别为CD=1,BC=;△DEB的三边长分别为DE=2,BD=2.
在△ABC与△CDB中,,∴△ABC与△CDB不相似;
在△ABC与△DEB中,,∴△ABC∽△DEB.
11.解析 (1)如图,点D是所求作的点(答案不唯一),此时△ABD∽△BCA.
(2)证明:∵AB=,AD=1,
∴,
∴,∴△ABD∽△BCA.
12.B ∵,∠A=∠A,∴△AED∽△ABC,故②正确;∵△AED∽△ABC,∴∠B=∠AED,由题中条件无法得出∠AED=∠ADE,故①错误.故选B.
13.B 选项A,∵公共角为∠B,,且,∴阴影三角形与△ABC不相似;选项B,∵公共角为∠A,,∴阴影三角形与△ABC相似;选项C,∵公共角为∠B,,且,∴阴影三角形与△ABC不相似;选项D,∵公共角为∠C,,且,∴阴影三角形与△ABC不相似.故选B.
14.2
解析 ∵AD=3,CD=1,∴AC=4.∵∠BAD=∠CAB,∴当时,△ADB∽△ABC,∴.
15.证明 ∵四边形ABCD是正方形,BP=3PC,Q是CD的中点,
∴CP=AD,
∴=2,
又∵∠ADQ=∠QCP=90°,
∴△ADQ∽△QCP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十七章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第2课时 相似三角形的判定(1)
基础过关全练
知识点4 相似三角形的判定方法——“三边定理”
8.(2022广西桂林灌阳期末)将一个三角形的各边都缩小到原来的后,得到的新三角形与原三角形( )
A.一定不相似 B.不一定相似
C.全等 D.一定相似
9.(2022天津模拟)如图所示,由边长为1的小正方形组成的网格中相似的两个三角形是( )
A.①与② B.①与③
C.③与④ D.②与③
10.(2021辽宁抚顺顺城模拟)如图,在6×2的正方形网格中有△ABC、△CDB、△DEB,其中与△ABC相似的是 .(△ABC除外)
11.(2022福建泉州南安模拟)如图,A、B、C三点均在边长为1的小正方形组成的网格的格点上.
(1)请在图中标出点D,连接AD,BD,使得△ABD与△CBA相似;
(2)试证明上述结论.
知识点5 相似三角形的判定方法——“两边夹角定理”
12.【反A字模型】(2023贵州铜仁期末)如图,在△ABC中,D,E分别是AB,AC边上的点,连接DE,已知.根据以上条件,关于下列两个结论:①∠ADE=∠B;②△AED∽△ABC,判断正确的是( )
A.①正确,②错误 B.①错误,②正确
C.两个都正确 D.两个都错误
13.(2023河北石家庄高邑期末)在三角形纸片ABC中,AB=9,AC=6,BC=12,下列沿虚线剪下的阴影三角形与△ABC相似的是( )
14.(2022江苏无锡新吴期中)如图,在△ABC中,D是AC边上的一点,AD=3,CD=1,要使△ADB∽△ABC,则AB的长为 .
15.(2022福建龙岩新罗月考)如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
答案全解全析
基础过关全练
8.D ∵将一个三角形的各边都缩小到原来的,∴新三角形的各边与原三角形的对应边的比值都为,∴新三角形与原三角形相似.故选D.
9.B 图形①的三边长分别为;图形②的三边长分别为3,;图形③的三边长分别为2,2;图形④的三边长分别为,∴①与③相似.故选B.
10.△DEB
解析 设小正方形的边长为1,则△ABC的三边长分别为AB=1,AC=;△CDB的三边长分别为CD=1,BC=;△DEB的三边长分别为DE=2,BD=2.
在△ABC与△CDB中,,∴△ABC与△CDB不相似;
在△ABC与△DEB中,,∴△ABC∽△DEB.
11.解析 (1)如图,点D是所求作的点(答案不唯一),此时△ABD∽△BCA.
(2)证明:∵AB=,AD=1,
∴,
∴,∴△ABD∽△BCA.
12.B ∵,∠A=∠A,∴△AED∽△ABC,故②正确;∵△AED∽△ABC,∴∠B=∠AED,由题中条件无法得出∠AED=∠ADE,故①错误.故选B.
13.B 选项A,∵公共角为∠B,,且,∴阴影三角形与△ABC不相似;选项B,∵公共角为∠A,,∴阴影三角形与△ABC相似;选项C,∵公共角为∠B,,且,∴阴影三角形与△ABC不相似;选项D,∵公共角为∠C,,且,∴阴影三角形与△ABC不相似.故选B.
14.2
解析 ∵AD=3,CD=1,∴AC=4.∵∠BAD=∠CAB,∴当时,△ADB∽△ABC,∴.
15.证明 ∵四边形ABCD是正方形,BP=3PC,Q是CD的中点,
∴CP=AD,
∴=2,
又∵∠ADQ=∠QCP=90°,
∴△ADQ∽△QCP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
