27.2.1.3 相似三角形的判定(2)课时练(含解析)
文档属性
| 名称 | 27.2.1.3 相似三角形的判定(2)课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 604.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 21:40:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十七章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时 相似三角形的判定(2)
基础过关全练
知识点6 相似三角形的判定方法——“两角定理”
16.(2023河北唐山丰南期末)在三角形纸片ABC中,∠A=76°,∠B=34°.将纸片沿虚线剪开,下列四种方式中剪下的阴影三角形与原三角形相似的是( )
A.①② B.②④ C.①③ D.③④
17.(2023山西忻州代县期末)将含60°角的直角三角板ABC(∠A=60°)与含45°角的直角三角板BCD按如图所示的方式放置,它们的斜边AC与斜边BD相交于点E.下列结论正确的是( )
A.△ABE∽△CDE B.△ABE∽△BCE
C.△BCE∽△DCE D.△ABC∽△DCB
18.(2023黑龙江齐齐哈尔龙沙三模)如图,在△ABC中,∠ABC=∠C=
∠BDC=∠AED=72°,则图中相似三角形共有( )
A.2对 B.3对 C.4对 D.5对
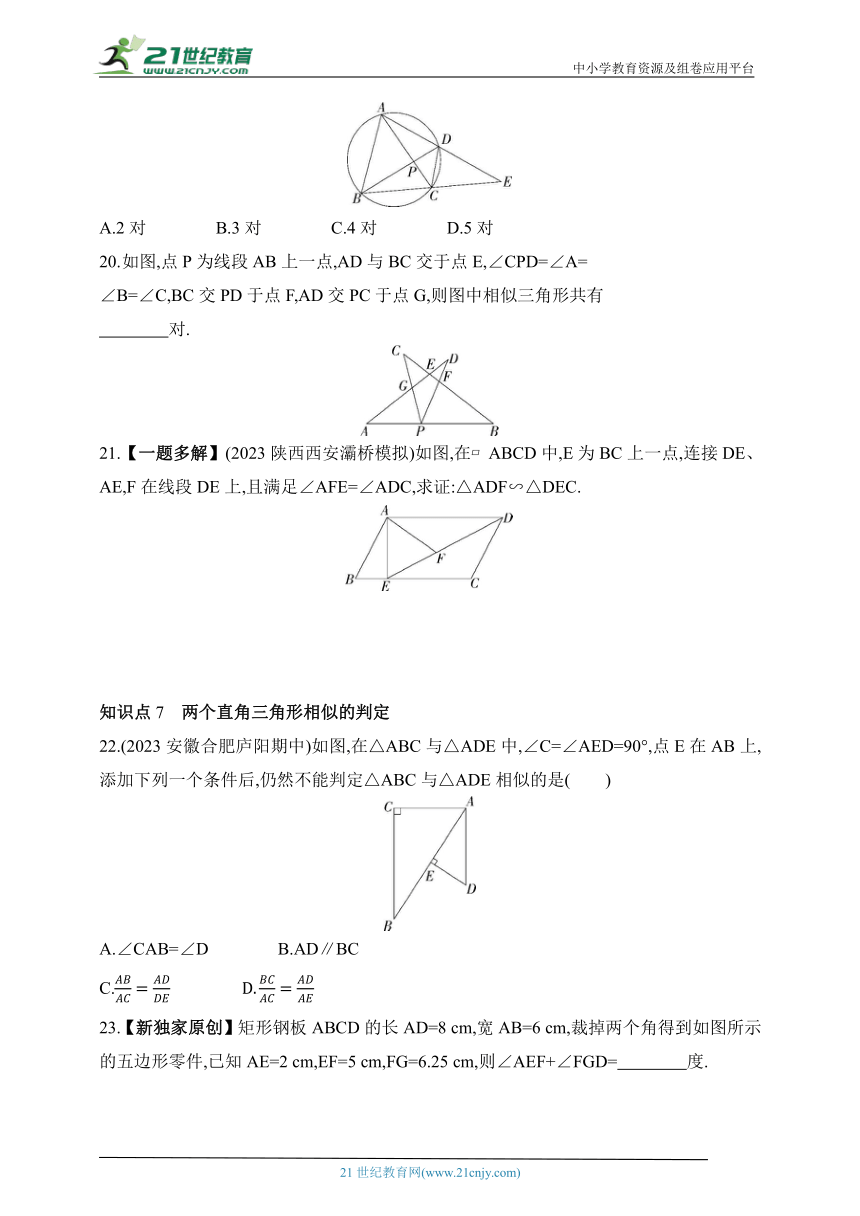
19.如图,点A、B、C、D在同一个圆上,弦AC、BD相交于点P,AD、BC的延长线交于点E,则图中相似三角形共有( )
A.2对 B.3对 C.4对 D.5对
如图,点P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=
∠B=∠C,BC交PD于点F,AD交PC于点G,则图中相似三角形共有
对.
21.【一题多解】(2023陕西西安灞桥模拟)如图,在 ABCD中,E为BC上一点,连接DE、AE,F在线段DE上,且满足∠AFE=∠ADC,求证:△ADF∽△DEC.
知识点7 两个直角三角形相似的判定
22.(2023安徽合肥庐阳期中)如图,在△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,添加下列一个条件后,仍然不能判定△ABC与△ADE相似的是( )
A.∠CAB=∠D B.AD∥BC
C.
23.【新独家原创】矩形钢板ABCD的长AD=8 cm,宽AB=6 cm,裁掉两个角得到如图所示的五边形零件,已知AE=2 cm,EF=5 cm,FG=6.25 cm,则∠AEF+∠FGD= 度.
能力提升全练
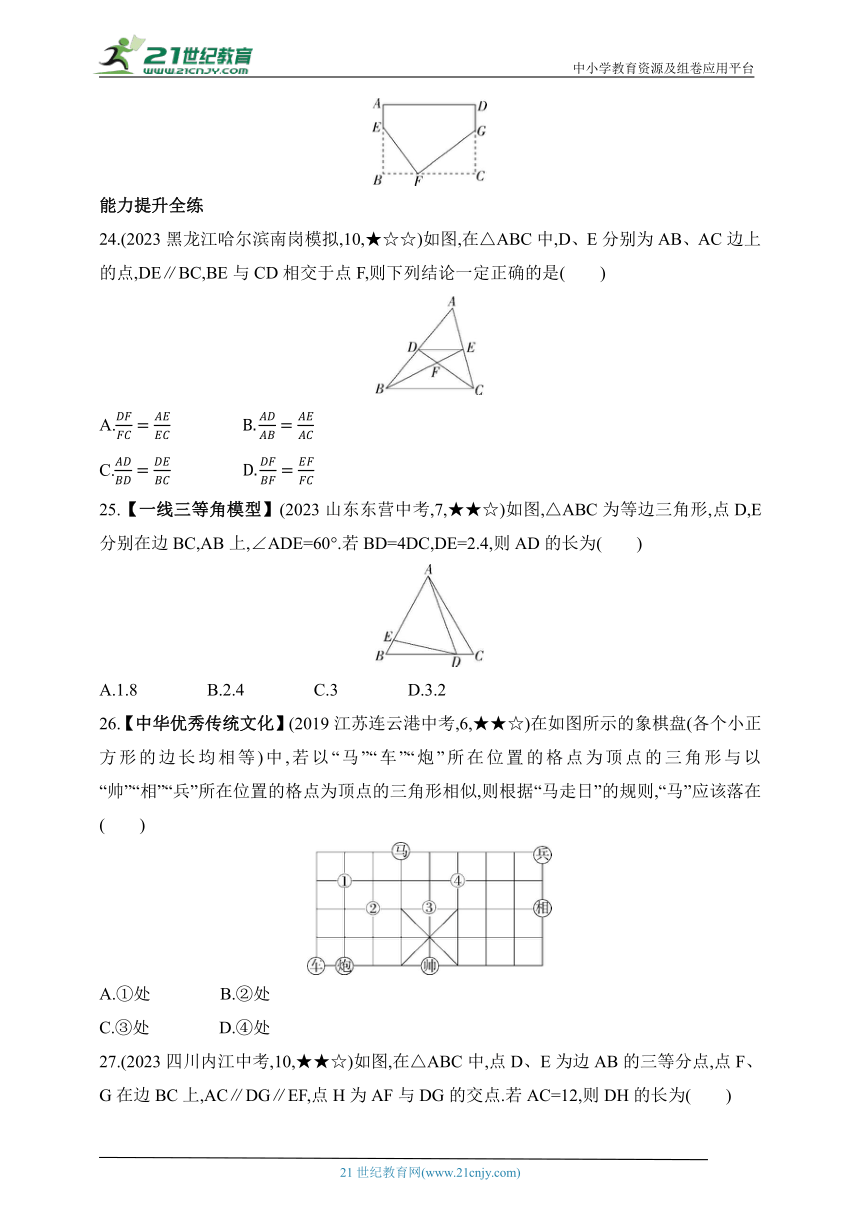
24.(2023黑龙江哈尔滨南岗模拟,10,★☆☆)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
A.
C.
25.【一线三等角模型】(2023山东东营中考,7,★★☆)如图,△ABC为等边三角形,点D,E分别在边BC,AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为( )
A.1.8 B.2.4 C.3 D.3.2
26.【中华优秀传统文化】(2019江苏连云港中考,6,★★☆)在如图所示的象棋盘(各个小正方形的边长均相等)中,若以“马”“车”“炮”所在位置的格点为顶点的三角形与以“帅”“相”“兵”所在位置的格点为顶点的三角形相似,则根据“马走日”的规则,“马”应该落在( )
A.①处 B.②处
C.③处 D.④处
27.(2023四川内江中考,10,★★☆)如图,在△ABC中,点D、E为边AB的三等分点,点F、G在边BC上,AC∥DG∥EF,点H为AF与DG的交点.若AC=12,则DH的长为( )
A.1 B.
C.2 D.3
28.(2022浙江杭州拱墅开学测试,7,★★☆)如图,菱形ABCD∽菱形AEFG,菱形AEFG的顶点G在菱形ABCD的BC边上运动,GF与AB相交于点H,∠E=60°,若CG=6,AH=14,则菱形ABCD的边长为( )
A.18
C.18 D.16
29.【新考向·开放型试题】(2022湖南邵阳中考,18,★☆☆)如图,在△ABC中,点D在AB边上,点E在AC边上,请添加一个条件: ,使△ADE∽△ABC.
30.(2021江苏连云港中考,16,★★☆)如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D.若BF=3FE,则= .
31.【分类讨论思想】(2023辽宁大连甘井子期末,16,★★☆)在△ABC中,AB=8,BC=16,AP=BP,点Q是BC边上一个动点,当BQ= 时,△BPQ与△BAC相似.
32.(2022安徽合肥庐阳三模,20,★★☆)如图,锐角△ABC内接于☉O,∠BAC的平分线AG交BC于点F,交☉O于点G,连接BG.
(1)求证:△ABG∽△AFC;
(2)已知点E在线段AF上(不与点A、点F重合),点D在线段AE上(不与点A、点E重合),∠ABD=∠CBE,求证:BG2=GE·GD.
素养探究全练
33.【推理能力】如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、B,与反比例函数y=(x>0)的图象交于点C,点P是反比例函数y=(x>0)图象上的一点,作PQ⊥x轴于点Q,连接OP.当点P的坐标为
时,△OPQ与△OAB相似.
34.【推理能力】【函数思想】如图,在矩形ABCD中,AB=6,BC=8,E是边BC上的动点,连接AE,过点E作EF⊥AE,与CD边交于点F,连接AF,则AF的最小值为 .
35.【推理能力】(2022江苏无锡中考)如图,边长为6的等边三角形ABC内接于☉O,点D为AC上的动点(点A、C除外),BD的延长线交☉O于点E,连接CE.
(1)求证:△CED∽△BAD;
(2)当DC=2AD时,求CE的长.
答案全解全析
基础过关全练
16.C ∵∠A=76°,∠B=34°,∴∠C=70°.①中,阴影三角形有两角分别是76°和34°,因此与原三角形相似;②中,阴影三角形有两角分别是34°和34°,不能推出和原三角形相似;③中,阴影三角形有两角分别是70°和34°,因此与原三角形相似;④中,阴影三角形有两角分别是70°和70°,不能推出和原三角形相似,所以阴影三角形与原三角形相似的为①③.故选C.
17.A 在Rt△ABC中,∠ABC=90°,∠A=60°,∴∠ACB=30°.
∵∠BCD=90°,∴∠ECD=∠BCD-∠ACB=90°-30°=60°,∴∠A=∠ECD.又∵∠AEB=∠CED,∴△ABE∽△CDE.故选A.
C ∵∠AED=∠ABC=72°,∴DE∥BC,∴△AED∽△ABC,
∵∠ABC=∠C=∠BDC,∴△ABC∽△BCD,∴△AED∽△BCD,
∵∠ABC=∠C=72°,∴∠A=36°,∵∠ADE=72°,∠BDC=72°,
∴∠BDE=36°,∴∠BDE=∠A,又∵∠EBD=∠ABD,∴△EBD∽△DBA,故图中相似三角形共有4对.故选C.
C ∵∠E为公共角,∠CAE=∠DBE,∴△ECA∽△EDB;∵∠E为公共角,∠EDC=∠ABE(由∠EDC和∠ABE都是∠ADC的补角,可得∠EDC=∠ABE),∴△EDC∽△EBA;∵∠DAC=∠DBC,∠APD=
∠BPC,∴△ADP∽△BCP;∵∠BAC=∠BDC,∠APB=∠DPC,∴△ABP∽△DCP,共4对相似三角形.故选C.
20.7
解析 ∵∠CPD=∠A=∠B=∠C,∴△ABE∽△BCP∽△CPF,此时有3对相似三角形;∵∠A=∠C,∠AGP=∠CGE,∴△AGP∽△CGE;
∵∠CPD=∠A,∠D为公共角,∴△APD∽△PGD;∵∠CPD=∠A=∠B,∠BPC=∠BPF+∠CPD=∠A+∠AGP,∴∠BPF=∠AGP,∴△AGP∽△BPF,∴△CGE∽△BPF.综上所述,共有7对相似三角形.
21.证明 证法一:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADC+∠C=180°,∠ADF=∠DEC.
∵∠AFE+∠AFD=180°,∠AFE=∠ADC,
∴∠C=∠AFD,
∴△ADF∽△DEC.
证法二:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠DEC.
∵∠AFE=∠ADC,且∠AFE=∠ADF+∠DAF,∠ADC=∠ADF+∠CDE,
∴∠DAF=∠CDE,
∴△ADF∽△DEC.
22.D 选项A,∵∠C=∠AED=90°,∠CAB=∠D,∴△ACB∽△DEA,不合题意;选项B,∵AD∥BC,∴∠B=∠DAE,又∵∠C=∠AED=90°,∴△ACB∽△DEA,不合题意;选项C,∵∠C=∠AED=90°,又由,∴Rt△ACB∽Rt△DEA,不合题意.故选D.
23.270
解析 ∵四边形ABCD是矩形,AD=8 cm,∴∠B=∠C=90°,BC=AD=
8 cm.∵AB=6 cm,AE=2 cm,∴BE=4 cm.在Rt△BEF中,EF=5 cm,
∴BF==3(cm),∴CF=BC-BF=8-3=5(cm).在△BEF和△CFG中,,又∵∠B=∠C=90°,
∴Rt△BEF∽Rt△CFG,∴∠BEF=∠CFG.∵∠AEF=180°-∠BEF,
∠FGD=∠C+∠CFG=90°+∠BEF,
∴∠AEF+∠FGD=180°-∠BEF+90°+∠BEF=270°.
能力提升全练
24.B ∵DE∥BC,∴△ADE∽△ABC,△DEF∽△CBF,∴,∴A、C、D错误,B正确,故选B.
25.C ∵△ABC是等边三角形,∴BC=AC,∠B=∠C=60°,
∴∠CAD+∠ADC=120°,∵∠ADE=60°,∴∠BDE+∠ADC=120°,
∴∠CAD=∠BDE,∴△ADC∽△DEB,∴,∵BD=4DC,
∴设DC=x,则BD=4x,∴BC=AC=5x,∴,∴AD=3.故选C.
模型解读 一线三等角模型:有三个等角的顶点在同一条直线上的基本几何图形.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且∠DEF=∠B=∠C,则△BDE∽△CEF.
26.B 设象棋盘中各个小正方形的边长都为1,由题图得,以“帅”“相”“兵”所在位置的格点为顶点的三角形的三边的长分别为2、2、4.“车”“炮”之间的距离为1,“炮”与②之间的距离为,“车”与②之间的距离为2,∴“马”应该落在②处.故选B.
27.C ∵点D、E为边AB的三等分点,∴AD=DE=EB,
∴AB=3BE,AE=2AD,∵EF∥AC,∴△BEF∽△BAC,
∴EF∶AC=BE∶AB,∵AC=12,AB=3BE,∴EF∶12=BE∶3BE,∴EF=4.∵DG∥EF,∴△ADH∽△AEF,∴DH∶EF=AD∶AE,∵EF=4,AE=2AD,∴DH∶4=AD∶2AD,∴DH=2.故选C.
C 如图,连接AC.∵菱形ABCD∽菱形AEFG,
∴∠B=∠E=∠AGF=60°,AB=BC,∴△ABC是等边三角形,
∴∠ACB=60°,设AB=BC=AC=a,则BH=a-14,BG=a-6,
∵∠AGB=∠AGH+∠BGH=∠ACG+∠CAG,∠AGH=∠ACG=60°,
∴∠BGH=∠CAG.又∵∠B=∠ACG,∴△BGH∽△CAG,∴
,∴a2-20a+36=0,∴a=18或a=2(舍去),∴AB=18.故选C.
29.DE∥BC(或∠ADE=∠B或∠AED=∠C或等,答案不唯一)
解析 当添加DE∥BC时,由“平行定理”可得△ADE∽△ABC;
∵∠A=∠A,∴当添加∠ADE=∠B或∠AED=∠C时,由“两角定理” 可得△ADE∽△ABC;
∵∠A=∠A,∴当添加时,由“两边夹角定理”可得△ADE∽△ABC.
30.
解析 如图,过点E作EG∥DC交AD于G,得△AGE∽△ADC.∵BE是△ABC的中线,∴点E是AC的中点,∴
.∵GE∥BD,∴△GFE∽△DFB,∴
.
31.2或8
解析 ∵AB=8,AP=BP,∴BP=4.当△BPQ∽△BAC时,,解得BQ=8;当△BPQ∽△BCA时,,解得BQ=2,综上所述,当BQ=2或8时,△BPQ与△BAC相似.
32.证明 (1)∵AG平分∠BAC,∴∠BAG=∠FAC.
又∵∠G=∠C,∴△ABG∽△AFC.
(2)∵∠CAG=∠CBG,∠BAG=∠CAG,
∴∠BAG=∠CBG.
∵∠ABD=∠CBE,
∴∠BDG=∠BAG+∠ABD=∠CBG+∠CBE=∠EBG.
又∵∠DGB=∠BGE,
∴△DGB∽△BGE,
∴,∴BG2=GE·GD.
素养探究全练
33.
解析 设点P的坐标为(a,b)(a>0,b>0),则PQ=b,OQ=a,∵点P在反比例函数y=(x>0)的图象上,∴ab=3①.把x=0代入y=x+3,得y=3,把y=0代入y=x+3,得x=-4,∴AO=4,BO=3.分两种情况:(1)若△OPQ∽△ABO,则,即②,由①②及a>0,b>0得;
(2)若△OPQ∽△BAO,则,即③,由①③及a>0,b>0得.
综上,点P的坐标为.
34.
解析 设BE的长为x,CF的长为y,则CE=BC-BE=8-x,∵AB⊥BC,EF⊥AE,DC⊥BC,∴∠ABE=∠AEF=∠ECF=90°,∴∠BAE+∠AEB=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF,∴Rt△ABE∽Rt△ECF,∴,即,∴y最大=.当CF=时,DF=6-,此时AF最小,AF=.
35.解析 (1)证明:∵∠A与∠E是所对的圆周角,
∴∠A=∠E.
又∵∠CDE=∠BDA,
∴△CED∽△BAD.
(2)如图,过点D作DF⊥EC于点F,
∵△ABC是边长为6的等边三角形,
∴∠A=60°,AC=AB=6.
∵DC=2AD,∴AD=2,DC=4.
∵△CED∽△BAD,
∴=3,
∴EC=3DE.
∵∠E=∠A=60°,DF⊥EC,
∴∠EDF=90°-60°=30°,
∴DE=2EF.
设EF=x,则DE=2x,DF=x,EC=6x,∴FC=5x,
在Rt△DFC中,DF2+FC2=DC2,
∴(x)2+(5x)2=42,
解得x=或x=-(舍去),
∴EC=6x=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十七章 相似
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时 相似三角形的判定(2)
基础过关全练
知识点6 相似三角形的判定方法——“两角定理”
16.(2023河北唐山丰南期末)在三角形纸片ABC中,∠A=76°,∠B=34°.将纸片沿虚线剪开,下列四种方式中剪下的阴影三角形与原三角形相似的是( )
A.①② B.②④ C.①③ D.③④
17.(2023山西忻州代县期末)将含60°角的直角三角板ABC(∠A=60°)与含45°角的直角三角板BCD按如图所示的方式放置,它们的斜边AC与斜边BD相交于点E.下列结论正确的是( )
A.△ABE∽△CDE B.△ABE∽△BCE
C.△BCE∽△DCE D.△ABC∽△DCB
18.(2023黑龙江齐齐哈尔龙沙三模)如图,在△ABC中,∠ABC=∠C=
∠BDC=∠AED=72°,则图中相似三角形共有( )
A.2对 B.3对 C.4对 D.5对
19.如图,点A、B、C、D在同一个圆上,弦AC、BD相交于点P,AD、BC的延长线交于点E,则图中相似三角形共有( )
A.2对 B.3对 C.4对 D.5对
如图,点P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=
∠B=∠C,BC交PD于点F,AD交PC于点G,则图中相似三角形共有
对.
21.【一题多解】(2023陕西西安灞桥模拟)如图,在 ABCD中,E为BC上一点,连接DE、AE,F在线段DE上,且满足∠AFE=∠ADC,求证:△ADF∽△DEC.
知识点7 两个直角三角形相似的判定
22.(2023安徽合肥庐阳期中)如图,在△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,添加下列一个条件后,仍然不能判定△ABC与△ADE相似的是( )
A.∠CAB=∠D B.AD∥BC
C.
23.【新独家原创】矩形钢板ABCD的长AD=8 cm,宽AB=6 cm,裁掉两个角得到如图所示的五边形零件,已知AE=2 cm,EF=5 cm,FG=6.25 cm,则∠AEF+∠FGD= 度.
能力提升全练
24.(2023黑龙江哈尔滨南岗模拟,10,★☆☆)如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
A.
C.
25.【一线三等角模型】(2023山东东营中考,7,★★☆)如图,△ABC为等边三角形,点D,E分别在边BC,AB上,∠ADE=60°.若BD=4DC,DE=2.4,则AD的长为( )
A.1.8 B.2.4 C.3 D.3.2
26.【中华优秀传统文化】(2019江苏连云港中考,6,★★☆)在如图所示的象棋盘(各个小正方形的边长均相等)中,若以“马”“车”“炮”所在位置的格点为顶点的三角形与以“帅”“相”“兵”所在位置的格点为顶点的三角形相似,则根据“马走日”的规则,“马”应该落在( )
A.①处 B.②处
C.③处 D.④处
27.(2023四川内江中考,10,★★☆)如图,在△ABC中,点D、E为边AB的三等分点,点F、G在边BC上,AC∥DG∥EF,点H为AF与DG的交点.若AC=12,则DH的长为( )
A.1 B.
C.2 D.3
28.(2022浙江杭州拱墅开学测试,7,★★☆)如图,菱形ABCD∽菱形AEFG,菱形AEFG的顶点G在菱形ABCD的BC边上运动,GF与AB相交于点H,∠E=60°,若CG=6,AH=14,则菱形ABCD的边长为( )
A.18
C.18 D.16
29.【新考向·开放型试题】(2022湖南邵阳中考,18,★☆☆)如图,在△ABC中,点D在AB边上,点E在AC边上,请添加一个条件: ,使△ADE∽△ABC.
30.(2021江苏连云港中考,16,★★☆)如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D.若BF=3FE,则= .
31.【分类讨论思想】(2023辽宁大连甘井子期末,16,★★☆)在△ABC中,AB=8,BC=16,AP=BP,点Q是BC边上一个动点,当BQ= 时,△BPQ与△BAC相似.
32.(2022安徽合肥庐阳三模,20,★★☆)如图,锐角△ABC内接于☉O,∠BAC的平分线AG交BC于点F,交☉O于点G,连接BG.
(1)求证:△ABG∽△AFC;
(2)已知点E在线段AF上(不与点A、点F重合),点D在线段AE上(不与点A、点E重合),∠ABD=∠CBE,求证:BG2=GE·GD.
素养探究全练
33.【推理能力】如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、B,与反比例函数y=(x>0)的图象交于点C,点P是反比例函数y=(x>0)图象上的一点,作PQ⊥x轴于点Q,连接OP.当点P的坐标为
时,△OPQ与△OAB相似.
34.【推理能力】【函数思想】如图,在矩形ABCD中,AB=6,BC=8,E是边BC上的动点,连接AE,过点E作EF⊥AE,与CD边交于点F,连接AF,则AF的最小值为 .
35.【推理能力】(2022江苏无锡中考)如图,边长为6的等边三角形ABC内接于☉O,点D为AC上的动点(点A、C除外),BD的延长线交☉O于点E,连接CE.
(1)求证:△CED∽△BAD;
(2)当DC=2AD时,求CE的长.
答案全解全析
基础过关全练
16.C ∵∠A=76°,∠B=34°,∴∠C=70°.①中,阴影三角形有两角分别是76°和34°,因此与原三角形相似;②中,阴影三角形有两角分别是34°和34°,不能推出和原三角形相似;③中,阴影三角形有两角分别是70°和34°,因此与原三角形相似;④中,阴影三角形有两角分别是70°和70°,不能推出和原三角形相似,所以阴影三角形与原三角形相似的为①③.故选C.
17.A 在Rt△ABC中,∠ABC=90°,∠A=60°,∴∠ACB=30°.
∵∠BCD=90°,∴∠ECD=∠BCD-∠ACB=90°-30°=60°,∴∠A=∠ECD.又∵∠AEB=∠CED,∴△ABE∽△CDE.故选A.
C ∵∠AED=∠ABC=72°,∴DE∥BC,∴△AED∽△ABC,
∵∠ABC=∠C=∠BDC,∴△ABC∽△BCD,∴△AED∽△BCD,
∵∠ABC=∠C=72°,∴∠A=36°,∵∠ADE=72°,∠BDC=72°,
∴∠BDE=36°,∴∠BDE=∠A,又∵∠EBD=∠ABD,∴△EBD∽△DBA,故图中相似三角形共有4对.故选C.
C ∵∠E为公共角,∠CAE=∠DBE,∴△ECA∽△EDB;∵∠E为公共角,∠EDC=∠ABE(由∠EDC和∠ABE都是∠ADC的补角,可得∠EDC=∠ABE),∴△EDC∽△EBA;∵∠DAC=∠DBC,∠APD=
∠BPC,∴△ADP∽△BCP;∵∠BAC=∠BDC,∠APB=∠DPC,∴△ABP∽△DCP,共4对相似三角形.故选C.
20.7
解析 ∵∠CPD=∠A=∠B=∠C,∴△ABE∽△BCP∽△CPF,此时有3对相似三角形;∵∠A=∠C,∠AGP=∠CGE,∴△AGP∽△CGE;
∵∠CPD=∠A,∠D为公共角,∴△APD∽△PGD;∵∠CPD=∠A=∠B,∠BPC=∠BPF+∠CPD=∠A+∠AGP,∴∠BPF=∠AGP,∴△AGP∽△BPF,∴△CGE∽△BPF.综上所述,共有7对相似三角形.
21.证明 证法一:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADC+∠C=180°,∠ADF=∠DEC.
∵∠AFE+∠AFD=180°,∠AFE=∠ADC,
∴∠C=∠AFD,
∴△ADF∽△DEC.
证法二:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADF=∠DEC.
∵∠AFE=∠ADC,且∠AFE=∠ADF+∠DAF,∠ADC=∠ADF+∠CDE,
∴∠DAF=∠CDE,
∴△ADF∽△DEC.
22.D 选项A,∵∠C=∠AED=90°,∠CAB=∠D,∴△ACB∽△DEA,不合题意;选项B,∵AD∥BC,∴∠B=∠DAE,又∵∠C=∠AED=90°,∴△ACB∽△DEA,不合题意;选项C,∵∠C=∠AED=90°,又由,∴Rt△ACB∽Rt△DEA,不合题意.故选D.
23.270
解析 ∵四边形ABCD是矩形,AD=8 cm,∴∠B=∠C=90°,BC=AD=
8 cm.∵AB=6 cm,AE=2 cm,∴BE=4 cm.在Rt△BEF中,EF=5 cm,
∴BF==3(cm),∴CF=BC-BF=8-3=5(cm).在△BEF和△CFG中,,又∵∠B=∠C=90°,
∴Rt△BEF∽Rt△CFG,∴∠BEF=∠CFG.∵∠AEF=180°-∠BEF,
∠FGD=∠C+∠CFG=90°+∠BEF,
∴∠AEF+∠FGD=180°-∠BEF+90°+∠BEF=270°.
能力提升全练
24.B ∵DE∥BC,∴△ADE∽△ABC,△DEF∽△CBF,∴,∴A、C、D错误,B正确,故选B.
25.C ∵△ABC是等边三角形,∴BC=AC,∠B=∠C=60°,
∴∠CAD+∠ADC=120°,∵∠ADE=60°,∴∠BDE+∠ADC=120°,
∴∠CAD=∠BDE,∴△ADC∽△DEB,∴,∵BD=4DC,
∴设DC=x,则BD=4x,∴BC=AC=5x,∴,∴AD=3.故选C.
模型解读 一线三等角模型:有三个等角的顶点在同一条直线上的基本几何图形.如图,在△ABC中,D、E、F分别在AB、BC、AC上,且∠DEF=∠B=∠C,则△BDE∽△CEF.
26.B 设象棋盘中各个小正方形的边长都为1,由题图得,以“帅”“相”“兵”所在位置的格点为顶点的三角形的三边的长分别为2、2、4.“车”“炮”之间的距离为1,“炮”与②之间的距离为,“车”与②之间的距离为2,∴“马”应该落在②处.故选B.
27.C ∵点D、E为边AB的三等分点,∴AD=DE=EB,
∴AB=3BE,AE=2AD,∵EF∥AC,∴△BEF∽△BAC,
∴EF∶AC=BE∶AB,∵AC=12,AB=3BE,∴EF∶12=BE∶3BE,∴EF=4.∵DG∥EF,∴△ADH∽△AEF,∴DH∶EF=AD∶AE,∵EF=4,AE=2AD,∴DH∶4=AD∶2AD,∴DH=2.故选C.
C 如图,连接AC.∵菱形ABCD∽菱形AEFG,
∴∠B=∠E=∠AGF=60°,AB=BC,∴△ABC是等边三角形,
∴∠ACB=60°,设AB=BC=AC=a,则BH=a-14,BG=a-6,
∵∠AGB=∠AGH+∠BGH=∠ACG+∠CAG,∠AGH=∠ACG=60°,
∴∠BGH=∠CAG.又∵∠B=∠ACG,∴△BGH∽△CAG,∴
,∴a2-20a+36=0,∴a=18或a=2(舍去),∴AB=18.故选C.
29.DE∥BC(或∠ADE=∠B或∠AED=∠C或等,答案不唯一)
解析 当添加DE∥BC时,由“平行定理”可得△ADE∽△ABC;
∵∠A=∠A,∴当添加∠ADE=∠B或∠AED=∠C时,由“两角定理” 可得△ADE∽△ABC;
∵∠A=∠A,∴当添加时,由“两边夹角定理”可得△ADE∽△ABC.
30.
解析 如图,过点E作EG∥DC交AD于G,得△AGE∽△ADC.∵BE是△ABC的中线,∴点E是AC的中点,∴
.∵GE∥BD,∴△GFE∽△DFB,∴
.
31.2或8
解析 ∵AB=8,AP=BP,∴BP=4.当△BPQ∽△BAC时,,解得BQ=8;当△BPQ∽△BCA时,,解得BQ=2,综上所述,当BQ=2或8时,△BPQ与△BAC相似.
32.证明 (1)∵AG平分∠BAC,∴∠BAG=∠FAC.
又∵∠G=∠C,∴△ABG∽△AFC.
(2)∵∠CAG=∠CBG,∠BAG=∠CAG,
∴∠BAG=∠CBG.
∵∠ABD=∠CBE,
∴∠BDG=∠BAG+∠ABD=∠CBG+∠CBE=∠EBG.
又∵∠DGB=∠BGE,
∴△DGB∽△BGE,
∴,∴BG2=GE·GD.
素养探究全练
33.
解析 设点P的坐标为(a,b)(a>0,b>0),则PQ=b,OQ=a,∵点P在反比例函数y=(x>0)的图象上,∴ab=3①.把x=0代入y=x+3,得y=3,把y=0代入y=x+3,得x=-4,∴AO=4,BO=3.分两种情况:(1)若△OPQ∽△ABO,则,即②,由①②及a>0,b>0得;
(2)若△OPQ∽△BAO,则,即③,由①③及a>0,b>0得.
综上,点P的坐标为.
34.
解析 设BE的长为x,CF的长为y,则CE=BC-BE=8-x,∵AB⊥BC,EF⊥AE,DC⊥BC,∴∠ABE=∠AEF=∠ECF=90°,∴∠BAE+∠AEB=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF,∴Rt△ABE∽Rt△ECF,∴,即,∴y最大=.当CF=时,DF=6-,此时AF最小,AF=.
35.解析 (1)证明:∵∠A与∠E是所对的圆周角,
∴∠A=∠E.
又∵∠CDE=∠BDA,
∴△CED∽△BAD.
(2)如图,过点D作DF⊥EC于点F,
∵△ABC是边长为6的等边三角形,
∴∠A=60°,AC=AB=6.
∵DC=2AD,∴AD=2,DC=4.
∵△CED∽△BAD,
∴=3,
∴EC=3DE.
∵∠E=∠A=60°,DF⊥EC,
∴∠EDF=90°-60°=30°,
∴DE=2EF.
设EF=x,则DE=2x,DF=x,EC=6x,∴FC=5x,
在Rt△DFC中,DF2+FC2=DC2,
∴(x)2+(5x)2=42,
解得x=或x=-(舍去),
∴EC=6x=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
