27.2.3 相似三角形应用举例课时练(含解析)
文档属性
| 名称 | 27.2.3 相似三角形应用举例课时练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 749.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-02 21:42:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十七章 相似
27.2 相似三角形
27.2.3 相似三角形应用举例
基础过关全练
知识点1 利用相似测量高度
1.(2023四川宜宾叙州期末)数学实践课上,小明在测量教学楼高度时,先测出教学楼落在地面上的影长BA为20米(如图),然后在A处树立一根高3米的标杆,测得标杆的影长AC为4米,则楼高( )
A.10米
B.12米
C.15米
D.25米
2.【跨学科·物理】(2023黑龙江哈尔滨南岗四模)小明设计的用激光笔测量城墙高度的示意图如图所示,在点P处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,AB=1.2米,BP=1.8米,PD=12米,那么城墙CD的高度为( )
A.6米 B.8米 C.10米 D.18米
3.【中华优秀传统文化】据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD(点A、B的对应点分别是点C、D).若物体AB的高为6 cm,小孔O到物体和实像的水平距离BE、CE分别为8 cm、6 cm,则实像CD的高度为 cm.
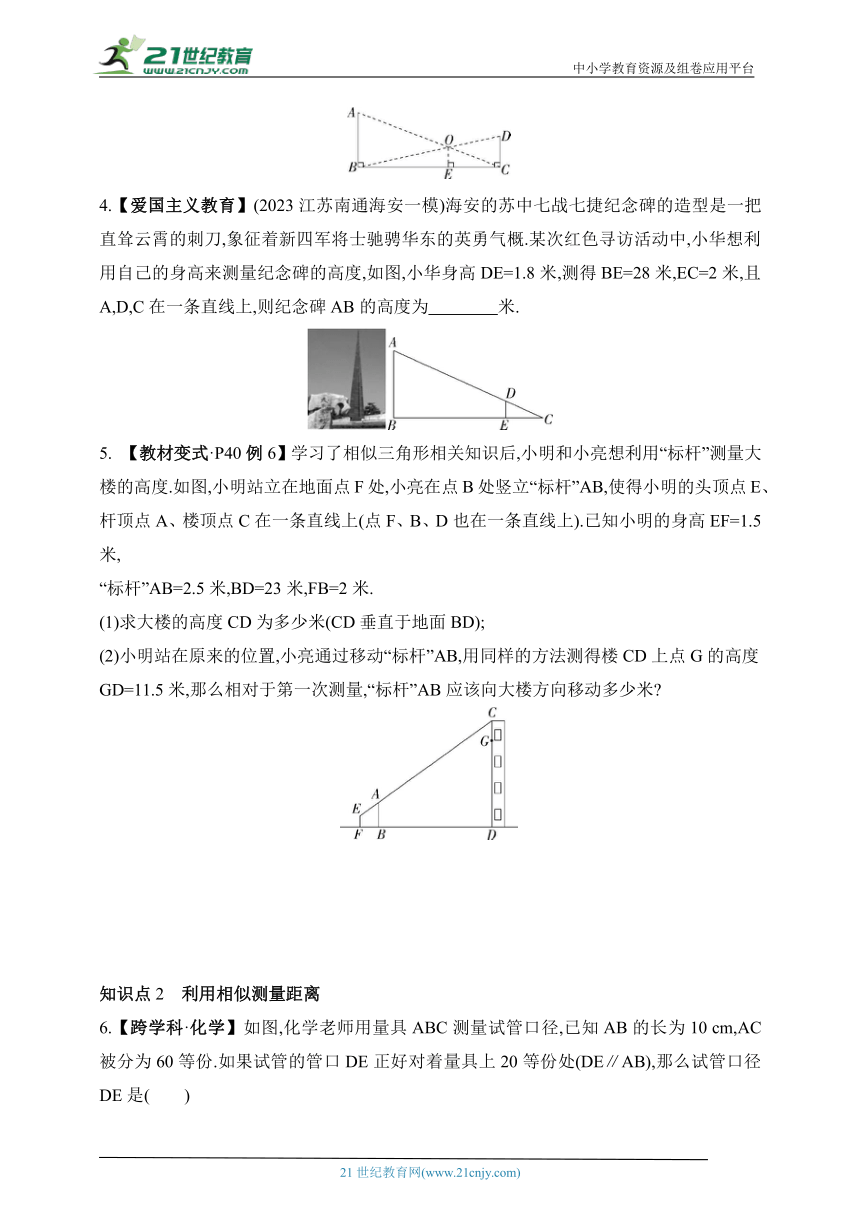
4.【爱国主义教育】(2023江苏南通海安一模)海安的苏中七战七捷纪念碑的造型是一把直耸云霄的刺刀,象征着新四军将士驰骋华东的英勇气概.某次红色寻访活动中,小华想利用自己的身高来测量纪念碑的高度,如图,小华身高DE=1.8米,测得BE=28米,EC=2米,且A,D,C在一条直线上,则纪念碑AB的高度为 米.
【教材变式·P40例6】学习了相似三角形相关知识后,小明和小亮想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,小亮在点B处竖立“标杆”AB,使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高EF=1.5米,
“标杆”AB=2.5米,BD=23米,FB=2米.
(1)求大楼的高度CD为多少米(CD垂直于地面BD);
(2)小明站在原来的位置,小亮通过移动“标杆”AB,用同样的方法测得楼CD上点G的高度GD=11.5米,那么相对于第一次测量,“标杆”AB应该向大楼方向移动多少米
知识点2 利用相似测量距离
6.【跨学科·化学】如图,化学老师用量具ABC测量试管口径,已知AB的长为10 cm,AC被分为60等份.如果试管的管口DE正好对着量具上20等份处(DE∥AB),那么试管口径DE是( )
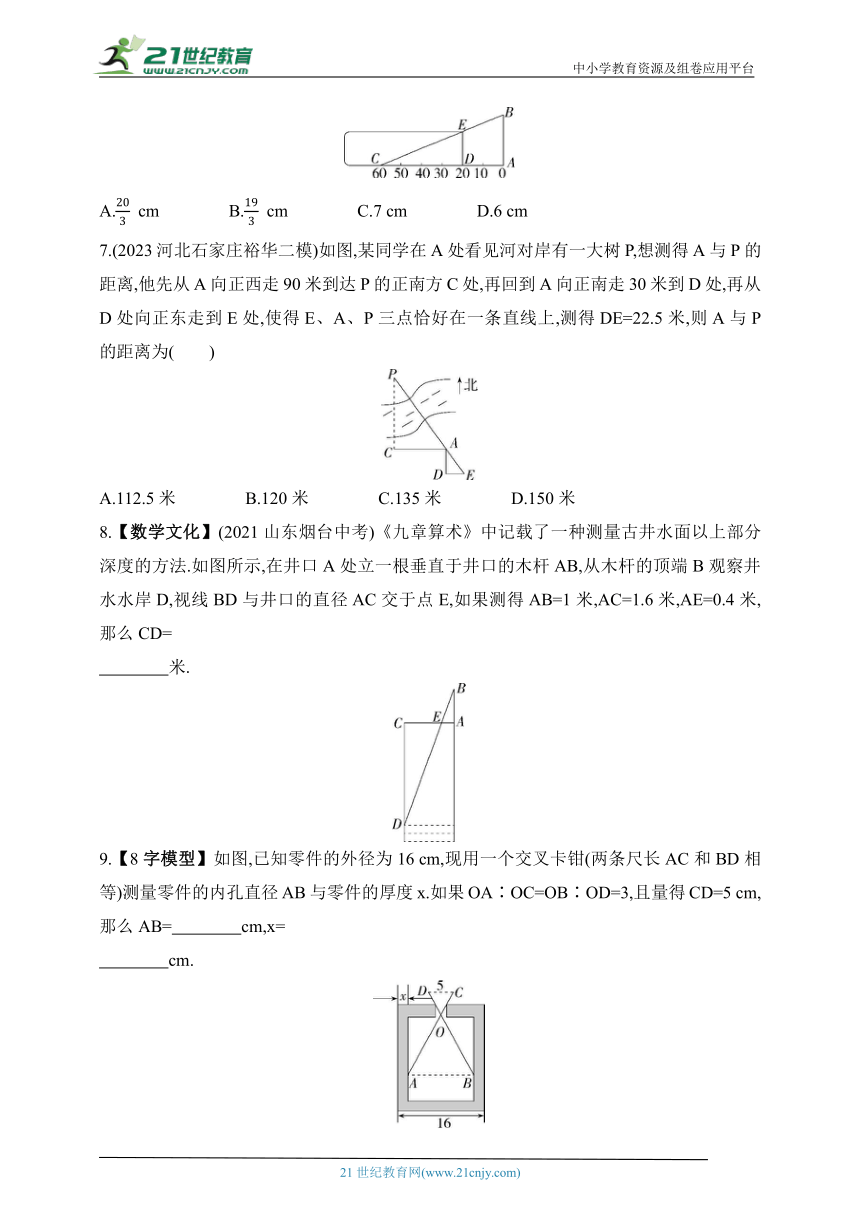
A. cm B. cm C.7 cm D.6 cm
7.(2023河北石家庄裕华二模)如图,某同学在A处看见河对岸有一大树P,想测得A与P的距离,他先从A向正西走90米到达P的正南方C处,再回到A向正南走30米到D处,再从D处向正东走到E处,使得E、A、P三点恰好在一条直线上,测得DE=22.5米,则A与P的距离为( )
A.112.5米 B.120米 C.135米 D.150米
8.【数学文化】(2021山东烟台中考)《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD=
米.
9.【8字模型】如图,已知零件的外径为16 cm,现用一个交叉卡钳(两条尺长AC和BD相等)测量零件的内孔直径AB与零件的厚度x.如果OA∶OC=OB∶OD=3,且量得CD=5 cm,那么AB= cm,x=
cm.
10.(2023陕西西安三模)某市为了加快城乡发展,保障市民出行方便,在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥(AF)的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB、AC的延长线上取点D、E,使得DE∥BC.经测量,BC=120 m,DE=210 m,且点E到河岸BC的距离为60 m.已知AF⊥BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度.
能力提升全练
11.(2023四川南充中考,6,★☆☆)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、平面镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6 m,同时量得小菲与镜子的水平距离为2 m,镜子与旗杆的水平距离为10 m,则旗杆高度为( )
A.6.4 m
B.8 m
C.9.6 m
D.12.5 m
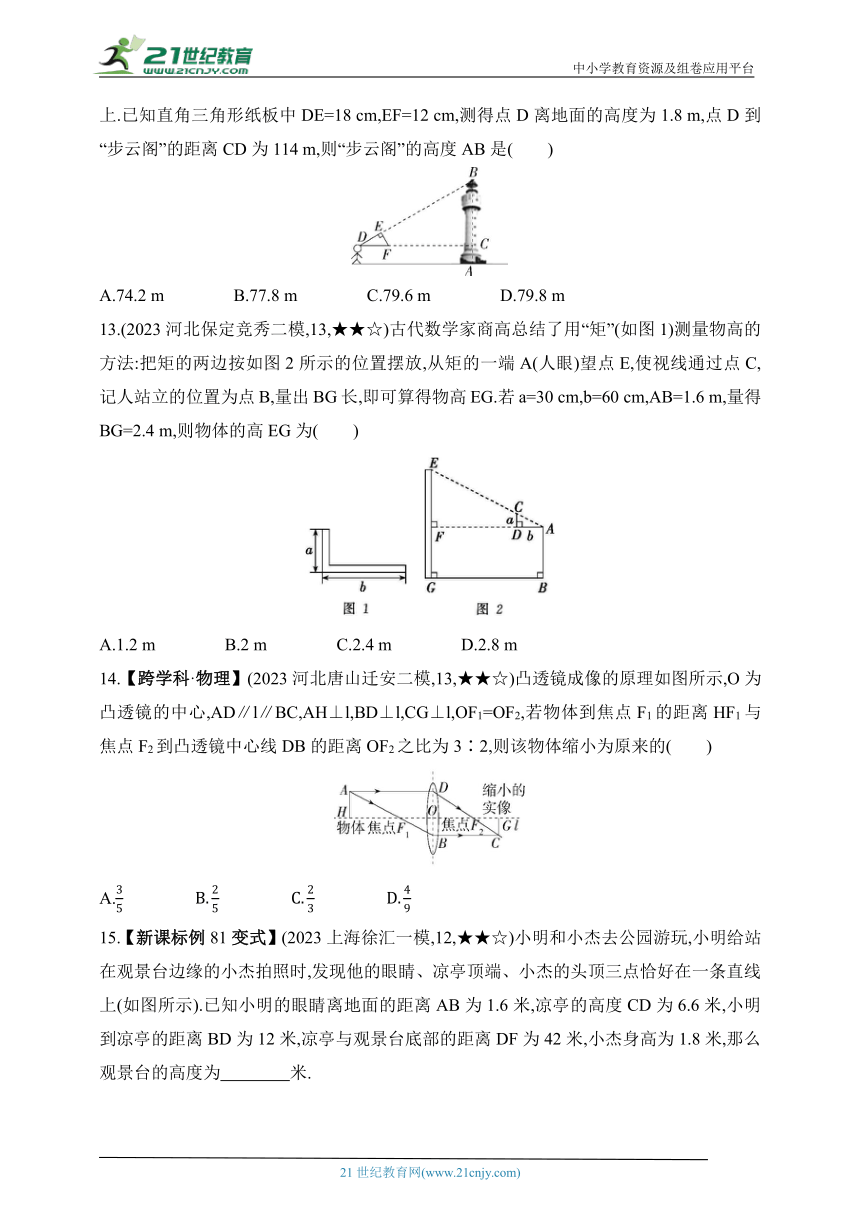
12.(2023广东深圳南山三模,7,★★☆)如图,李老师用自制的直角三角形纸板去测“步云阁”的高度,他调整直角三角形纸板的位置,设法使斜边DF保持水平,边DE与点B在同一直线上.已知直角三角形纸板中DE=18 cm,EF=12 cm,测得点D离地面的高度为1.8 m,点D到“步云阁”的距离CD为114 m,则“步云阁”的高度AB是( )
A.74.2 m B.77.8 m C.79.6 m D.79.8 m
13.(2023河北保定竞秀二模,13,★★☆)古代数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边按如图2所示的位置摆放,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.若a=30 cm,b=60 cm,AB=1.6 m,量得BG=2.4 m,则物体的高EG为( )
A.1.2 m B.2 m C.2.4 m D.2.8 m
14.【跨学科·物理】(2023河北唐山迁安二模,13,★★☆)凸透镜成像的原理如图所示,O为凸透镜的中心,AD∥l∥BC,AH⊥l,BD⊥l,CG⊥l,OF1=OF2,若物体到焦点F1的距离HF1与焦点F2到凸透镜中心线DB的距离OF2之比为3∶2,则该物体缩小为原来的( )
A.
15.【新课标例81变式】(2023上海徐汇一模,12,★★☆)小明和小杰去公园游玩,小明给站在观景台边缘的小杰拍照时,发现他的眼睛、凉亭顶端、小杰的头顶三点恰好在一条直线上(如图所示).已知小明的眼睛离地面的距离AB为1.6米,凉亭的高度CD为6.6米,小明到凉亭的距离BD为12米,凉亭与观景台底部的距离DF为42米,小杰身高为1.8米,那么观景台的高度为 米.
16.(2022江苏南京鼓楼期末,15,★★☆)如图,夜晚路灯下,小莉在点D处测得自己的影长DE=4 m,在点G处测得自己的影长DG=3 m,E、D、G、B在同一条直线上.已知小莉身高为1.6 m,则灯杆AB的高度为 m.
17.(2021广东肇庆端州期中,16,★★☆)如图,距离不远的两根电线杆高度均为3.2 m.在阳光照射下,第一根电线杆在平坦广场上的影长AB=4.8 m,第二根电线杆离墙的距离CD=3 m,且第二根电线杆的部分影子投射到墙上,则投射在墙上的影子DE的长度为 m.
素养探究全练
18.【应用意识】(2022江苏盐城中考)“跳眼法”是指用手指和眼睛估测距离的方法.
步骤:第一步:水平举起右臂,大拇指竖直向上,大臂与身体垂直;第二步:闭上左眼,调整位置,使得右眼、大拇指、被测物体在一条直线上;第三步:闭上右眼,睁开左眼,此时看到被测物体出现在大拇指左侧,与大拇指指向的位置有一段横向距离,参照被测物体的大小,估算横向距离;第四步:将横向距离乘10(人的手臂长度与眼距的比值一般为10),得到的值约为被测物体离观测点的距离值.
用“跳眼法”估测前方一辆汽车到观测点的距离的示意图如图所示,该汽车的长度大约为4米,则汽车到观测点的距离约为( )
A.40米 B.60米 C.80米 D.100米
19.【应用意识】(2023浙江温州模拟)如图,ED为一条宽为4米的河,河的西岸建有一道防洪堤,防洪堤与东岸的高度差为3米(即CE=3米),因为施工需要,现准备将东岸的泥沙通过滑轨送到西岸的防洪堤上,防洪堤上已经建好一座固定滑轨一端的钢架,现准备在东岸找一个点P作为另一端的固定点,已知吊篮的截面为直径为1米的半圆(直径MN=1米),绳子QM=QN=1.3米,钢架高度为2.2米(AB=2.2米),钢架距离防洪堤边缘0.5米(BC=0.5米).
(1)防洪堤边缘点C与东岸边缘点D之间的距离为 米;
(2)滑轨在运送货物时保持笔直,要想做到运输过程中吊篮一定不会碰到点C,则DP的长度至少保持 米.
20.【应用意识】【新考法】一块材料(△ABC)的形状是等腰三角形,底边BC=120 cm,高AD=120 cm.
(1)若把这块材料加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上(如图1),则这个正方形的边长为多少
(2)若把这块材料加工成正方体零件(如图2,阴影部分为正方体展开图),则这个正方体的表面积为多少
答案全解全析
基础过关全练
1.C ∵,即,∴楼高=15米.故选C.
2.B 由题意,得∠APB=∠CPD,∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,∴Rt△ABP∽Rt△CDP,∴,即,
∴CD=8(米).故选B.
3.4.5
解析 ∵AB∥CD,∴△OAB∽△OCD,∴,
∴CD=4.5 cm,即实像CD的高度为4.5 cm.
4.27
解析 由题意,得△CDE∽△CAB,∴DE∶AB=EC∶BC,
∵DE=1.8米,BE=28米,EC=2米,∴1.8∶AB=2∶30,解得AB=27(米).
5.解析 (1)如图,过点E作EH⊥CD于点H,交AB于点J,则四边形EFBJ,四边形EFDH都是矩形,
∴EF=BJ=DH=1.5米,BF=EJ=2米,DB=JH=23米,
∵AB=2.5米,∴AJ=AB-BJ=2.5-1.5=1(米),
∵AJ∥CH,∴△EAJ∽△ECH,
∴,∴CH=12.5(米),
∴CD=CH+DH=12.5+1.5=14(米).
∴大楼的高度CD为14米.
(2)如图,过点E作ET⊥CD于点T,交AB于点R.
∵AR∥GT,∴△AER∽△GET,
∴,
∴,∴ER=2.5(米),
∵2.5-2=0.5(米),
∴“标杆”AB应该向大楼方向移动0.5米.
A ∵DE∥AB,∴△CDE∽△CAB.∴DE∶AB=CD∶AC.
∴DE∶10=40∶60.∴DE= cm,即试管口径DE是 cm.故选A.
D 由题意,得AC∥DE,∠C=∠D=90°,则△ACP∽△EDA,故,∵AC=90米,AD=30米,DE=22.5米,∴PC=120(米),
∴AP==150(米),即A与P的距离为150米.故选D.
8.3
解析 ∵AB⊥AC,CD⊥AC,∴AB∥CD,∴△ABE∽△CDE,∴,∵AC=1.6米,AE=0.4米,∴CE=AC-AE=1.6-0.4=1.2(米),又AB=1米,∴,∴CD=3(米).
9.15;
解析 ∵OA∶OC=OB∶OD=3,∠COD=∠AOB,∴△COD∽△AOB,∴AB∶CD=3,∵CD=5 cm,∴AB=15 cm,∵零件的外径为16 cm,∴零件的厚度x为(16-15)÷2=(cm).
10.解析 如图,过E作EG⊥BC于G,
∵DE∥BC,∴△ABC∽△ADE,
∴.
∵AF⊥BC,EG⊥BC,∴AF∥EG,
∴△ACF∽△ECG,
∴,即,解得AF=80(m),
∴桥AF的长度为80 m.
能力提升全练
11.B 如图,∵AB⊥BD,DE⊥BD,∴∠ABC=∠EDC=90°.∵∠ACB=
∠DCE,∴△ABC∽△EDC,∴,即,∴DE=8(m).故选B.
B 在△DEF和△DCB中,∵∠D=∠D,∠DEF=∠DCB=90°,
∴△DEF∽△DCB,∴,即,解得BC=76(m),∵AC=1.8 m,∴AB=AC+BC=1.8+76=77.8(m).故选B.
13.D 由题意可得,AF=BG=2.4 m,EF=EG-FG,FG=AB=1.6 m,CD=a=
0.3 m,AD=b=0.6 m,∴EF=EG-1.6,∵CD⊥AF,EF⊥AF,∴CD∥EF,∴△ADC∽△AFE,∴,即,解得EG=2.8 m.故选D.
14.C ∵BC∥l,CG⊥l,BO⊥l,∴四边形OBCG为矩形,∴OB=CG,∵物体到焦点F1的距离HF1与焦点F2到凸透镜中心线DB的距离OF2之比为3∶2,∴,∵AH⊥HO,BO⊥HO,∠AF1H=∠BF1O,∴△AHF1∽△BOF1,∴,∴物体缩小为原来的.故选C.
15.22.3
解析 如图,作AM⊥EF于M,交DC于N,∵CD=6.6米,AB=1.6米,∴CN=CD-AB=5米,FM=AB=1.6米,∵CN∥EM,∴△ACN∽△AEM,∴CN∶EM=AN∶AM,∴5∶EM=12∶54,∴EM=22.5(米),∴EF=EM+FM=22.5+1.6=24.1(米),∴观景台的高度为24.1-1.8=22.3米.
16.6.4
解析 ∵CD∥AB,∴△ECD∽△EAB,
∴,即,
∵FG∥AB,∴△DFG∽△DAB,∴,
即,解得BG=9(m),
∴,∴AB=6.4(m),即灯杆AB的高度为6.4 m.
17.1.2
解析 如图,过E作EF⊥CG于F,则EF=CD=3 m.由题意知CG=AH=3.2 m.设投射在墙上的影子DE的长度为x m,由题意可得△GFE∽△HAB,∴,即,解得x=1.2,经检验,x=1.2是原分式方程的解,∴影子DE的长度为1.2 m.
素养探究全练
18.C 在“跳眼法”中,被测物体离观测点的距离=横向距离×10.∵汽车的长度大约为4米,观察图形,横向距离大约是汽车的长度的2倍,∴横向距离大约是8米,∴汽车到观测点的距离约为8×10=80(米).故选C.
19.(1)5 (2)0.7
解析 (1)如图所示,连接CD,由题意可知∠CED=90°,CE=3米,DE=4米,则由勾股定理可得CD==5米.
如图所示,延长EC交AP于点G,过点Q作QK⊥MN于点K,延长AB与射线PE交于点O,∵QM=QN=1.3米,MN=1米,∴△QMN是等腰三角形,MK=米,∴QK==1.2米.滑轨在运送货物时保持笔直,要想做到运输过程中吊篮一定不会碰到点C,则CG长至少为1.2+0.5=1.7米,
以下分析CG长为1.7米的情况:∵∠AOP=∠GEP=90°,∠GPE=
∠APO,∴△GPE∽△APO,∴,设PD=x米,
则PE=(x+4)米,PO=x+4+0.5=(4.5+x)米,又GE=GC+CE=1.7+3=4.7米,AO=3+2.2=5.2米,∴,解得x=0.7.∴DP的长度至少保持0.7米.
20.解析 本题综合考查相似三角形与正方形.
(1)设正方形边长为x cm,
∵AD是△ABC的高,
∴∠ADB=90°.
∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AKE=∠ADB=90°,△AEH∽△ABC,
∴,∴x=60.
答:这个正方形的边长为60 cm.
(2)设小正方形边长为a cm,即MN=a cm,
∵AD为△ABC的高,
∴∠ADB=90°.
∵MN∥BC,
∴∠APM=∠ADB=90°,△AMN∽△ABC,
∴,
∴a=24,∴6a2=6×242=3 456.
答:正方体的表面积为3 456 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十七章 相似
27.2 相似三角形
27.2.3 相似三角形应用举例
基础过关全练
知识点1 利用相似测量高度
1.(2023四川宜宾叙州期末)数学实践课上,小明在测量教学楼高度时,先测出教学楼落在地面上的影长BA为20米(如图),然后在A处树立一根高3米的标杆,测得标杆的影长AC为4米,则楼高( )
A.10米
B.12米
C.15米
D.25米
2.【跨学科·物理】(2023黑龙江哈尔滨南岗四模)小明设计的用激光笔测量城墙高度的示意图如图所示,在点P处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,AB=1.2米,BP=1.8米,PD=12米,那么城墙CD的高度为( )
A.6米 B.8米 C.10米 D.18米
3.【中华优秀传统文化】据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD(点A、B的对应点分别是点C、D).若物体AB的高为6 cm,小孔O到物体和实像的水平距离BE、CE分别为8 cm、6 cm,则实像CD的高度为 cm.
4.【爱国主义教育】(2023江苏南通海安一模)海安的苏中七战七捷纪念碑的造型是一把直耸云霄的刺刀,象征着新四军将士驰骋华东的英勇气概.某次红色寻访活动中,小华想利用自己的身高来测量纪念碑的高度,如图,小华身高DE=1.8米,测得BE=28米,EC=2米,且A,D,C在一条直线上,则纪念碑AB的高度为 米.
【教材变式·P40例6】学习了相似三角形相关知识后,小明和小亮想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,小亮在点B处竖立“标杆”AB,使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高EF=1.5米,
“标杆”AB=2.5米,BD=23米,FB=2米.
(1)求大楼的高度CD为多少米(CD垂直于地面BD);
(2)小明站在原来的位置,小亮通过移动“标杆”AB,用同样的方法测得楼CD上点G的高度GD=11.5米,那么相对于第一次测量,“标杆”AB应该向大楼方向移动多少米
知识点2 利用相似测量距离
6.【跨学科·化学】如图,化学老师用量具ABC测量试管口径,已知AB的长为10 cm,AC被分为60等份.如果试管的管口DE正好对着量具上20等份处(DE∥AB),那么试管口径DE是( )
A. cm B. cm C.7 cm D.6 cm
7.(2023河北石家庄裕华二模)如图,某同学在A处看见河对岸有一大树P,想测得A与P的距离,他先从A向正西走90米到达P的正南方C处,再回到A向正南走30米到D处,再从D处向正东走到E处,使得E、A、P三点恰好在一条直线上,测得DE=22.5米,则A与P的距离为( )
A.112.5米 B.120米 C.135米 D.150米
8.【数学文化】(2021山东烟台中考)《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD=
米.
9.【8字模型】如图,已知零件的外径为16 cm,现用一个交叉卡钳(两条尺长AC和BD相等)测量零件的内孔直径AB与零件的厚度x.如果OA∶OC=OB∶OD=3,且量得CD=5 cm,那么AB= cm,x=
cm.
10.(2023陕西西安三模)某市为了加快城乡发展,保障市民出行方便,在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥(AF)的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB、AC的延长线上取点D、E,使得DE∥BC.经测量,BC=120 m,DE=210 m,且点E到河岸BC的距离为60 m.已知AF⊥BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度.
能力提升全练
11.(2023四川南充中考,6,★☆☆)如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、平面镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6 m,同时量得小菲与镜子的水平距离为2 m,镜子与旗杆的水平距离为10 m,则旗杆高度为( )
A.6.4 m
B.8 m
C.9.6 m
D.12.5 m
12.(2023广东深圳南山三模,7,★★☆)如图,李老师用自制的直角三角形纸板去测“步云阁”的高度,他调整直角三角形纸板的位置,设法使斜边DF保持水平,边DE与点B在同一直线上.已知直角三角形纸板中DE=18 cm,EF=12 cm,测得点D离地面的高度为1.8 m,点D到“步云阁”的距离CD为114 m,则“步云阁”的高度AB是( )
A.74.2 m B.77.8 m C.79.6 m D.79.8 m
13.(2023河北保定竞秀二模,13,★★☆)古代数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边按如图2所示的位置摆放,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.若a=30 cm,b=60 cm,AB=1.6 m,量得BG=2.4 m,则物体的高EG为( )
A.1.2 m B.2 m C.2.4 m D.2.8 m
14.【跨学科·物理】(2023河北唐山迁安二模,13,★★☆)凸透镜成像的原理如图所示,O为凸透镜的中心,AD∥l∥BC,AH⊥l,BD⊥l,CG⊥l,OF1=OF2,若物体到焦点F1的距离HF1与焦点F2到凸透镜中心线DB的距离OF2之比为3∶2,则该物体缩小为原来的( )
A.
15.【新课标例81变式】(2023上海徐汇一模,12,★★☆)小明和小杰去公园游玩,小明给站在观景台边缘的小杰拍照时,发现他的眼睛、凉亭顶端、小杰的头顶三点恰好在一条直线上(如图所示).已知小明的眼睛离地面的距离AB为1.6米,凉亭的高度CD为6.6米,小明到凉亭的距离BD为12米,凉亭与观景台底部的距离DF为42米,小杰身高为1.8米,那么观景台的高度为 米.
16.(2022江苏南京鼓楼期末,15,★★☆)如图,夜晚路灯下,小莉在点D处测得自己的影长DE=4 m,在点G处测得自己的影长DG=3 m,E、D、G、B在同一条直线上.已知小莉身高为1.6 m,则灯杆AB的高度为 m.
17.(2021广东肇庆端州期中,16,★★☆)如图,距离不远的两根电线杆高度均为3.2 m.在阳光照射下,第一根电线杆在平坦广场上的影长AB=4.8 m,第二根电线杆离墙的距离CD=3 m,且第二根电线杆的部分影子投射到墙上,则投射在墙上的影子DE的长度为 m.
素养探究全练
18.【应用意识】(2022江苏盐城中考)“跳眼法”是指用手指和眼睛估测距离的方法.
步骤:第一步:水平举起右臂,大拇指竖直向上,大臂与身体垂直;第二步:闭上左眼,调整位置,使得右眼、大拇指、被测物体在一条直线上;第三步:闭上右眼,睁开左眼,此时看到被测物体出现在大拇指左侧,与大拇指指向的位置有一段横向距离,参照被测物体的大小,估算横向距离;第四步:将横向距离乘10(人的手臂长度与眼距的比值一般为10),得到的值约为被测物体离观测点的距离值.
用“跳眼法”估测前方一辆汽车到观测点的距离的示意图如图所示,该汽车的长度大约为4米,则汽车到观测点的距离约为( )
A.40米 B.60米 C.80米 D.100米
19.【应用意识】(2023浙江温州模拟)如图,ED为一条宽为4米的河,河的西岸建有一道防洪堤,防洪堤与东岸的高度差为3米(即CE=3米),因为施工需要,现准备将东岸的泥沙通过滑轨送到西岸的防洪堤上,防洪堤上已经建好一座固定滑轨一端的钢架,现准备在东岸找一个点P作为另一端的固定点,已知吊篮的截面为直径为1米的半圆(直径MN=1米),绳子QM=QN=1.3米,钢架高度为2.2米(AB=2.2米),钢架距离防洪堤边缘0.5米(BC=0.5米).
(1)防洪堤边缘点C与东岸边缘点D之间的距离为 米;
(2)滑轨在运送货物时保持笔直,要想做到运输过程中吊篮一定不会碰到点C,则DP的长度至少保持 米.
20.【应用意识】【新考法】一块材料(△ABC)的形状是等腰三角形,底边BC=120 cm,高AD=120 cm.
(1)若把这块材料加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上(如图1),则这个正方形的边长为多少
(2)若把这块材料加工成正方体零件(如图2,阴影部分为正方体展开图),则这个正方体的表面积为多少
答案全解全析
基础过关全练
1.C ∵,即,∴楼高=15米.故选C.
2.B 由题意,得∠APB=∠CPD,∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,∴Rt△ABP∽Rt△CDP,∴,即,
∴CD=8(米).故选B.
3.4.5
解析 ∵AB∥CD,∴△OAB∽△OCD,∴,
∴CD=4.5 cm,即实像CD的高度为4.5 cm.
4.27
解析 由题意,得△CDE∽△CAB,∴DE∶AB=EC∶BC,
∵DE=1.8米,BE=28米,EC=2米,∴1.8∶AB=2∶30,解得AB=27(米).
5.解析 (1)如图,过点E作EH⊥CD于点H,交AB于点J,则四边形EFBJ,四边形EFDH都是矩形,
∴EF=BJ=DH=1.5米,BF=EJ=2米,DB=JH=23米,
∵AB=2.5米,∴AJ=AB-BJ=2.5-1.5=1(米),
∵AJ∥CH,∴△EAJ∽△ECH,
∴,∴CH=12.5(米),
∴CD=CH+DH=12.5+1.5=14(米).
∴大楼的高度CD为14米.
(2)如图,过点E作ET⊥CD于点T,交AB于点R.
∵AR∥GT,∴△AER∽△GET,
∴,
∴,∴ER=2.5(米),
∵2.5-2=0.5(米),
∴“标杆”AB应该向大楼方向移动0.5米.
A ∵DE∥AB,∴△CDE∽△CAB.∴DE∶AB=CD∶AC.
∴DE∶10=40∶60.∴DE= cm,即试管口径DE是 cm.故选A.
D 由题意,得AC∥DE,∠C=∠D=90°,则△ACP∽△EDA,故,∵AC=90米,AD=30米,DE=22.5米,∴PC=120(米),
∴AP==150(米),即A与P的距离为150米.故选D.
8.3
解析 ∵AB⊥AC,CD⊥AC,∴AB∥CD,∴△ABE∽△CDE,∴,∵AC=1.6米,AE=0.4米,∴CE=AC-AE=1.6-0.4=1.2(米),又AB=1米,∴,∴CD=3(米).
9.15;
解析 ∵OA∶OC=OB∶OD=3,∠COD=∠AOB,∴△COD∽△AOB,∴AB∶CD=3,∵CD=5 cm,∴AB=15 cm,∵零件的外径为16 cm,∴零件的厚度x为(16-15)÷2=(cm).
10.解析 如图,过E作EG⊥BC于G,
∵DE∥BC,∴△ABC∽△ADE,
∴.
∵AF⊥BC,EG⊥BC,∴AF∥EG,
∴△ACF∽△ECG,
∴,即,解得AF=80(m),
∴桥AF的长度为80 m.
能力提升全练
11.B 如图,∵AB⊥BD,DE⊥BD,∴∠ABC=∠EDC=90°.∵∠ACB=
∠DCE,∴△ABC∽△EDC,∴,即,∴DE=8(m).故选B.
B 在△DEF和△DCB中,∵∠D=∠D,∠DEF=∠DCB=90°,
∴△DEF∽△DCB,∴,即,解得BC=76(m),∵AC=1.8 m,∴AB=AC+BC=1.8+76=77.8(m).故选B.
13.D 由题意可得,AF=BG=2.4 m,EF=EG-FG,FG=AB=1.6 m,CD=a=
0.3 m,AD=b=0.6 m,∴EF=EG-1.6,∵CD⊥AF,EF⊥AF,∴CD∥EF,∴△ADC∽△AFE,∴,即,解得EG=2.8 m.故选D.
14.C ∵BC∥l,CG⊥l,BO⊥l,∴四边形OBCG为矩形,∴OB=CG,∵物体到焦点F1的距离HF1与焦点F2到凸透镜中心线DB的距离OF2之比为3∶2,∴,∵AH⊥HO,BO⊥HO,∠AF1H=∠BF1O,∴△AHF1∽△BOF1,∴,∴物体缩小为原来的.故选C.
15.22.3
解析 如图,作AM⊥EF于M,交DC于N,∵CD=6.6米,AB=1.6米,∴CN=CD-AB=5米,FM=AB=1.6米,∵CN∥EM,∴△ACN∽△AEM,∴CN∶EM=AN∶AM,∴5∶EM=12∶54,∴EM=22.5(米),∴EF=EM+FM=22.5+1.6=24.1(米),∴观景台的高度为24.1-1.8=22.3米.
16.6.4
解析 ∵CD∥AB,∴△ECD∽△EAB,
∴,即,
∵FG∥AB,∴△DFG∽△DAB,∴,
即,解得BG=9(m),
∴,∴AB=6.4(m),即灯杆AB的高度为6.4 m.
17.1.2
解析 如图,过E作EF⊥CG于F,则EF=CD=3 m.由题意知CG=AH=3.2 m.设投射在墙上的影子DE的长度为x m,由题意可得△GFE∽△HAB,∴,即,解得x=1.2,经检验,x=1.2是原分式方程的解,∴影子DE的长度为1.2 m.
素养探究全练
18.C 在“跳眼法”中,被测物体离观测点的距离=横向距离×10.∵汽车的长度大约为4米,观察图形,横向距离大约是汽车的长度的2倍,∴横向距离大约是8米,∴汽车到观测点的距离约为8×10=80(米).故选C.
19.(1)5 (2)0.7
解析 (1)如图所示,连接CD,由题意可知∠CED=90°,CE=3米,DE=4米,则由勾股定理可得CD==5米.
如图所示,延长EC交AP于点G,过点Q作QK⊥MN于点K,延长AB与射线PE交于点O,∵QM=QN=1.3米,MN=1米,∴△QMN是等腰三角形,MK=米,∴QK==1.2米.滑轨在运送货物时保持笔直,要想做到运输过程中吊篮一定不会碰到点C,则CG长至少为1.2+0.5=1.7米,
以下分析CG长为1.7米的情况:∵∠AOP=∠GEP=90°,∠GPE=
∠APO,∴△GPE∽△APO,∴,设PD=x米,
则PE=(x+4)米,PO=x+4+0.5=(4.5+x)米,又GE=GC+CE=1.7+3=4.7米,AO=3+2.2=5.2米,∴,解得x=0.7.∴DP的长度至少保持0.7米.
20.解析 本题综合考查相似三角形与正方形.
(1)设正方形边长为x cm,
∵AD是△ABC的高,
∴∠ADB=90°.
∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AKE=∠ADB=90°,△AEH∽△ABC,
∴,∴x=60.
答:这个正方形的边长为60 cm.
(2)设小正方形边长为a cm,即MN=a cm,
∵AD为△ABC的高,
∴∠ADB=90°.
∵MN∥BC,
∴∠APM=∠ADB=90°,△AMN∽△ABC,
∴,
∴a=24,∴6a2=6×242=3 456.
答:正方体的表面积为3 456 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
