27.3 位似课时练(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十七章 相似
27.3 位似
基础过关全练
知识点1 位似图形的定义
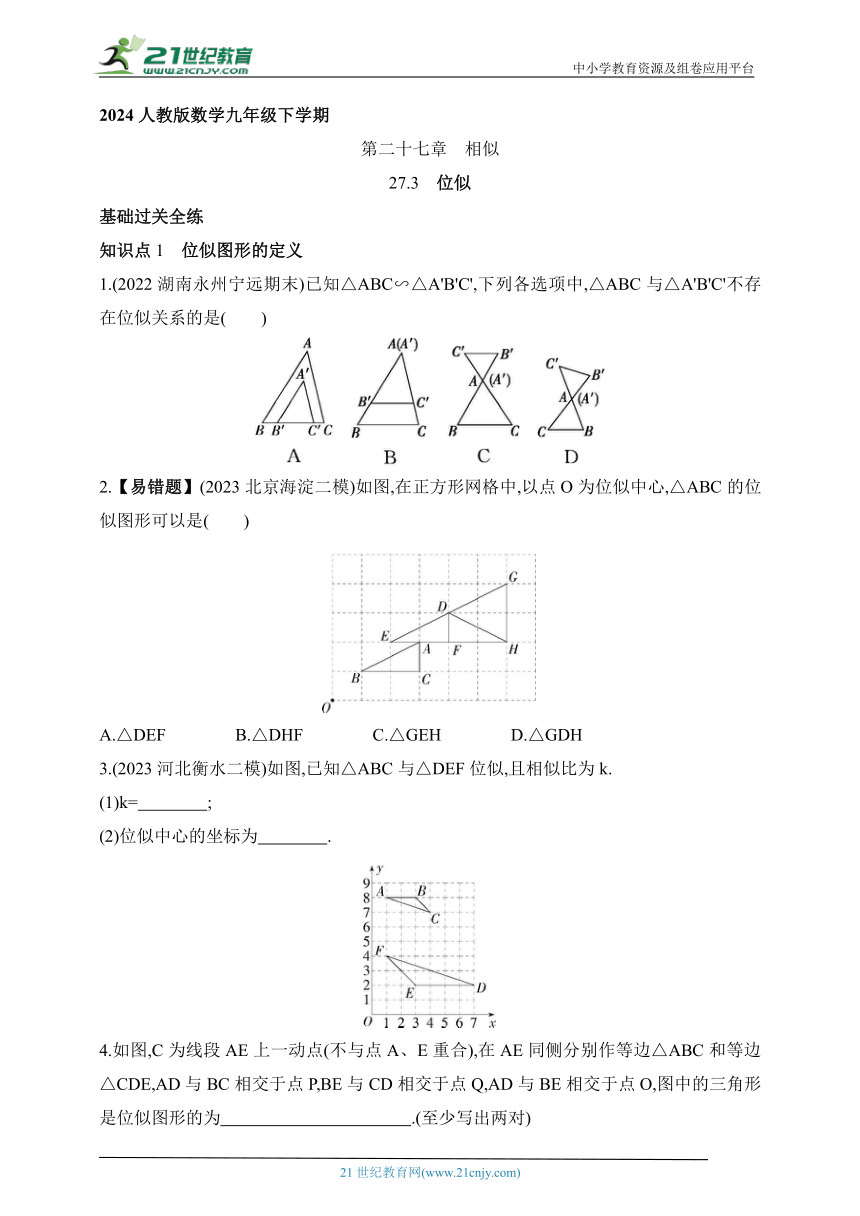
1.(2022湖南永州宁远期末)已知△ABC∽△A'B'C',下列各选项中,△ABC与△A'B'C'不存在位似关系的是( )
2.【易错题】(2023北京海淀二模)如图,在正方形网格中,以点O为位似中心,△ABC的位似图形可以是( )
A.△DEF B.△DHF C.△GEH D.△GDH
3.(2023河北衡水二模)如图,已知△ABC与△DEF位似,且相似比为k.
(1)k= ;
(2)位似中心的坐标为 .
4.如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,AD与BE相交于点O,图中的三角形是位似图形的为 .(至少写出两对)
知识点2 位似图形的性质
5.(2022山东滨州博兴期末)如图,以点O为位似中心,把△ABC各边放大到原来的2倍得到△A'B'C'.下列说法错误的是( )
A.△ABC∽△A'B'C' B.AO∶AA'=1∶2
C.AB∥A'B' D.直线CC'经过点O
6.(2022四川成都青白江月考)如图,在△ABC所在平面上任意取一点O(与A,B,C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点A1、B1、C1,再连接A1B1、A1C1、B1C1得到△A1B1C1,则下列说法不正确的是( )
A.△ABC与△A1B1C1是位似图形
B.△ABC与△A1B1C1是相似图形
C.△ABC与△A1B1C1的周长比为2∶1
D.△ABC与△A1B1C1的面积比为2∶1
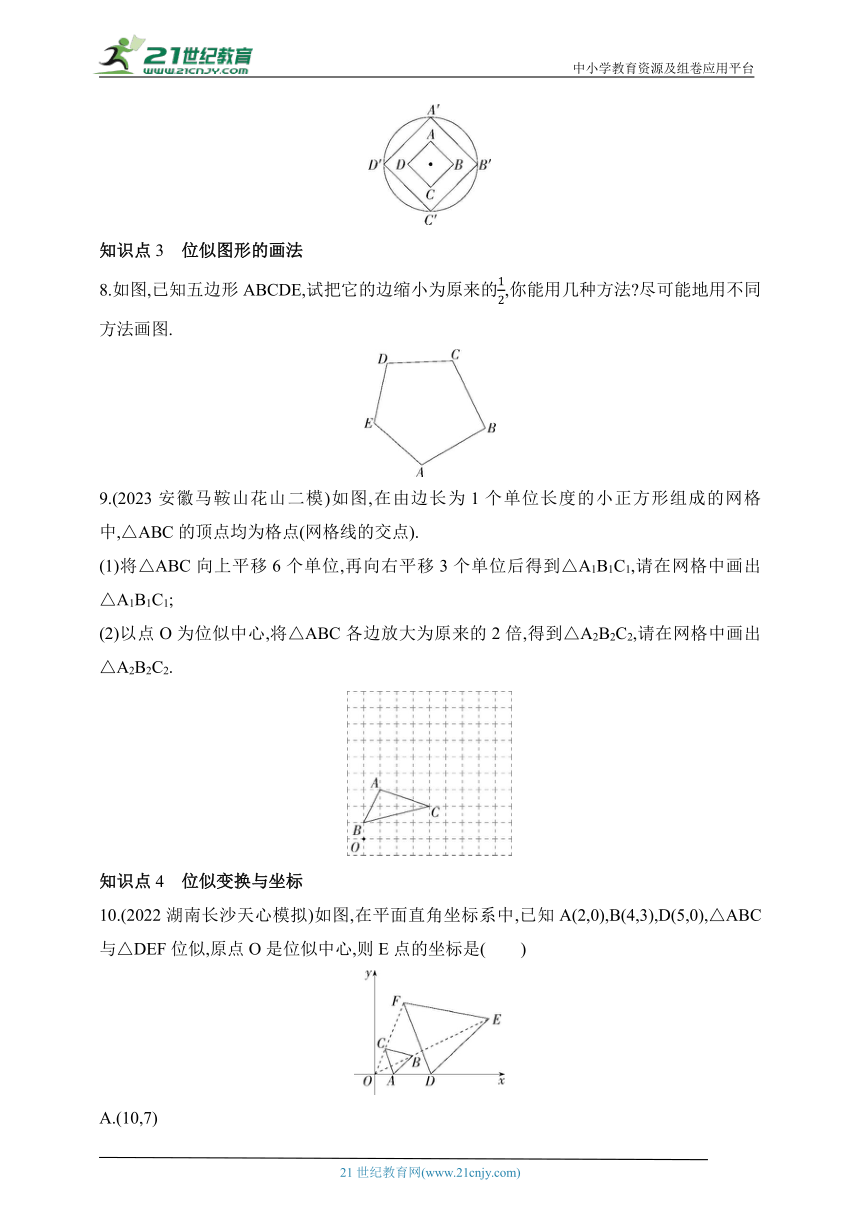
7.【中华优秀传统文化】(2023山东枣庄山亭期末)《墨子·天志》记载:“轮匠执其规、矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的面积为1,以它的对角线的交点为位似中心,作它的位似图形A'B'C'D',若AB∶A'B'=1∶2,则正方形A'B'C'D'的周长为 .
知识点3 位似图形的画法
8.如图,已知五边形ABCDE,试把它的边缩小为原来的,你能用几种方法 尽可能地用不同方法画图.
9.(2023安徽马鞍山花山二模)如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)将△ABC向上平移6个单位,再向右平移3个单位后得到△A1B1C1,请在网格中画出△A1B1C1;
(2)以点O为位似中心,将△ABC各边放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
知识点4 位似变换与坐标
10.(2022湖南长沙天心模拟)如图,在平面直角坐标系中,已知A(2,0),B(4,3),D(5,0),△ABC与△DEF位似,原点O是位似中心,则E点的坐标是( )
A.(10,7)
B.(8,7)
C.(10,7.5)
D.(8,6)
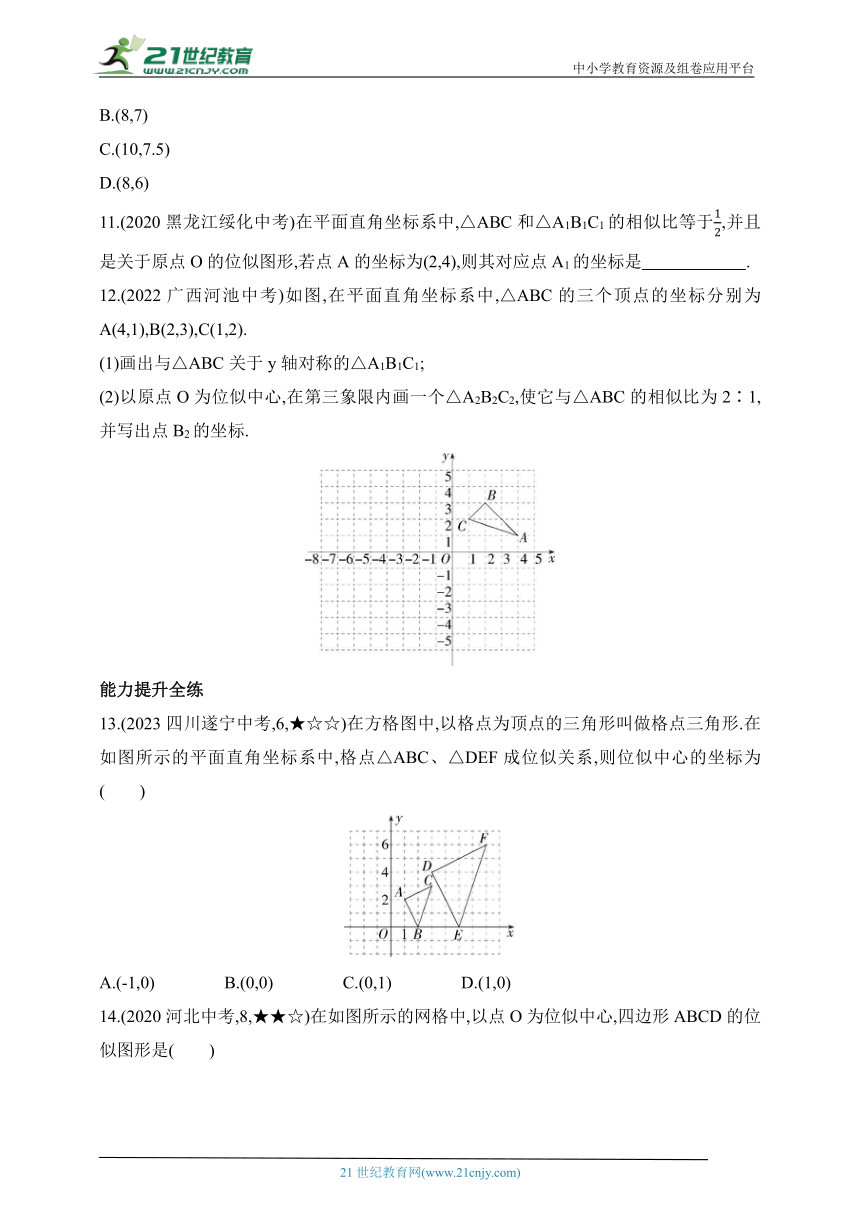
11.(2020黑龙江绥化中考)在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是 .
12.(2022广西河池中考)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).
(1)画出与△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,在第三象限内画一个△A2B2C2,使它与△ABC的相似比为2∶1,并写出点B2的坐标.
能力提升全练
13.(2023四川遂宁中考,6,★☆☆)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC、△DEF成位似关系,则位似中心的坐标为( )
A.(-1,0) B.(0,0) C.(0,1) D.(1,0)
14.(2020河北中考,8,★★☆)在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
15.【易错题】(2022山东青岛市北二模,6,★★☆)如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先将△ABC绕点(-1,0)顺时针旋转90°得到△A1B1C1,再以原点为位似中心作△A1B1C1的位似图形△A2B2C2,若△A1B1C1与△A2B2C2的相似比为1∶2,则点A2的坐标是( )
A.(4,2) B.(6,4)
C.(6,4)或(-6,-4) D.(4,2)或(-4,-2)
16.(2022广西河池罗城模拟,16,★★☆)如图,点A是反比例函数y=(x<0)图象上的一点,直线AD分别与x轴,y轴交于点D和C,AB⊥y轴于点B,则△ABC与△DOC是以点C为位似中心的位似图形,若△ABC与△DOC的相似比为1∶3,△ABC的面积为,则k的值为 .
17.(2023海南海口期末,19,★★☆)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2)
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似图形△OA1B1,使它与△OAB的相似比为2∶1,并写出点A的对应点A1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2,并写出点A2的坐标;
(3)判断△OA1B1与△O2A2B2能否是关于某一点M为位似中心的位似图形,若能,请在图中标出位似中心M,并写出点M的坐标.
素养探究全练
18.【运算能力】(2023湖北黄冈浠水一模)如图,AB和A'B'都与x轴垂直,A点的坐标是(2,4),△AOB和△A'OB'是位似三角形,且相似比是1∶3,点C是OA'的中点,反比例函数y=(x>0)的图象经过点C,与A'B'交于点D.则点D坐标为 .
19.【推理能力】【一题多解】(2023黑龙江绥化中考)如图,在平面直角坐标系中,△ABC与△AB'C'是以点A为位似中心的位似图形,相似比为1∶2,已知点A(2,0),点C(a,b),∠C=90°,则点C'的坐标为 .(结果用含a,b的式子表示)
答案全解全析
基础过关全练
1.D 选项D中两个三角形虽然是相似三角形,但对应边BC与B'C'不平行,不是位似图形.
故选D.
2.C 如图,∵△ABC与△GEH是相似图形,而且对应顶点的连线相交于点O,对应边互相平行,∴△ABC与△GEH是以O为位似中心的位似图形.
故选C.
易错点 未根据定义作对应顶点的连线而错选.
3.(1) (2)(3,6)
解析 (1)AB=2,BC=.
(2)如图所示:
位似中心的坐标为(3,6).
4.△ABP与△DCP,△ABE与△CQE(答案不唯一)
解析 ∵在等边△ABC和等边△CDE中,∠BAC=∠ACB=∠DCE=∠DEC=60°,∴AB∥CD,BC∥DE,∴△ABP∽△DCP,又∵△ABP与△DCP对应顶点的连线相交于点P,∴△ABP与△DCP是位似图形.同理,位似图形还有△ABE与△CQE,△ACP与△AED,△BCQ与△EDQ,△BPO与△EDO,△ABO与△DQO.此外,由题意可得△ABC和△CDE也是位似图形.
5.B ∵以点O为位似中心,把△ABC各边放大到原来的2倍得到△A'B'C',∴△ABC∽△A'B'C',AB∥A'B',直线CC'经过点O,AO∶AA'=1∶3,故A、C、D选项说法正确,不符合题意;B选项说法错误,符合题意.故选B.
6.D ∵点A1、B1、C1分别是OA、OB、OC的中点,∴A1B1∥AB,A1C1∥AC,B1C1∥BC,A1B1=BC,∴△ABC与△A1B1C1是位似图形,A正确;△ABC与△A1B1C1是相似图形,B正确;△ABC与△A1B1C1的周长比为2∶1,C正确;△ABC与△A1B1C1的面积比为4∶1,D错误.故选D.
7.8
解析 ∵正方形ABCD的面积为1,∴AB=1,∴正方形ABCD的周长为4.∵AB∶A'B'=1∶2,∴,∴正方形A'B'C'D'的周长=2×4=8.
8.解析 方法一:在五边形ABCDE的外部任取一点O,
连接OA,OB,OC,OD,OE;
分别取OA,OB,OC,OD,OE的中点A',B',C',D',E',
顺次连接A',B',C',D',E',A',
即得五边形A'B'C'D'E',如图.
方法二:在五边形ABCDE的外部任取一点O,
作射线AO,BO,CO,DO,EO;
在O的另一侧取点A',B',C',D',E',
使OA'=OC,
OD'=OE,
顺次连接A',B',C',D',E',A',
即得五边形A'B'C'D'E',如图.
方法三:在五边形的内部任取一点O,
连接OA,OB,OC,OD,OE;
分别取OA,OB,OC,OD,OE的中点A',B',C',D',E',
顺次连接A',B',C',D',E',A',
即得五边形A'B'C'D'E',如图.
方法四:在AB边上取一点O,连接CO,DO,EO;
取OA,OB,OC,OD,OE的中点A',B',C',D',E',
顺次连接B',C',D',E',A',
即得五边形A'B'C'D'E',如图.
方法五:以A点为位似中心,连接AC,AD;
分别取AB,AC,AD,AE的中点B',C',D',E',
顺次连接B',C',D',E',
即得五边形AB'C'D'E',如图.
(其他方法正确亦可)
9.解析 (1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
10.C ∵△ABC与△DEF位似,原点O是位似中心,而A(2,0),D(5,0),∴△DEF与△ABC的相似比为.∵B(4,3),∴E点的坐标为,即(10,7.5).
故选C.
11.(4,8)或(-4,-8)
解析 ∵△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,又点A的坐标为(2,4),∴点A的对应点A1的坐标为(2×2,2×4)或(-2×2,-2×4),即(4,8)或(-4,-8).
12.解析 (1)如图,△A1B1C1即为所求作的图形.
(2)如图,△A2B2C2即为所求作的图形,点B2的坐标为(-4,-6).
能力提升全练
13.A 如图,△ABC与△DEF的对应顶点的连线相交于点(-1,0),则位似中心的坐标为(-1,0).故选A.
14.A 观察图形或通过计算可知四边形ABCD是菱形,选项中,四边形NPMQ是菱形,另外三个四边形不是菱形,所以,以点O为位似中心,四边形ABCD的位似图形只能是四边形NPMQ.故选A.
15.D 如图,设点P的坐标为(-1,0),连接AP、A1P,过点A作AD⊥x轴于D,过点A1作A1E⊥x轴于E,
∵∠DAP+∠APD=90°,∠EPA1+∠APD=90°,
∴∠DAP=∠EPA1,
在△DAP和△EPA1中,
∴△DAP≌△EPA1(AAS),
∴A1E=DP=1,PE=AD=3,∴点A1的坐标为(2,1),
∵△A1B1C1与△A2B2C2是以原点为位似中心的位似图形,相似比为1∶2,
∴点A2的坐标是(4,2)或(-4,-2).故选D.
易错点 易忽视乘-k的情况(k为相似比).
16.-6
解析 如图,连接OA,∵△ABC与△DOC的相似比为1∶3,∴,∵S△ABC=,∴S△ABO=3,∴=3,∵k<0,∴k=-6.
17.解析 (1)如图,△OA1B1即为所求作的图形,A1(4,2).
(2)如图,△O2A2B2即为所求作的图形,A2(0,2).
(3)△OA1B1与△O2A2B2是关于点M(-4,2)为位似中心的位似图形.
素养探究全练
18.(6,3)
解析 ∵△AOB和△A'OB'是位似三角形,且相似比是1∶3,∴.∵点A的坐标是(2,4),∴OB=2,AB=4,∴,∴A'B'=12,OB'=6,∴A'(6,12).∵点C是OA'的中点,∴C(3,6),∴k=3×6=18,即反比例函数为y=.∵A'B'⊥x轴,∴xD=xA'=6,∴yD==3,即D(6,3).
19.(6-2a,-2b)
解析 解法一:过C作CM⊥AB于M,过C'作C'N⊥AB'于N,则∠ANC'=∠AMC=90°,∵△ABC与△AB'C'的相似比为1∶2,∴,∵∠NAC'=∠CAM,∴△ACM∽△AC'N,∴,∵点A(2,0),点C(a,b),∴OA=2,OM=a,CM=b,∴AM=a-2,∴,∴AN=2a-4,C'N=2b,∴ON=AN-OA=2a-6,∴点C'的坐标为(6-2a,-2b).
解法二(巧解):将△ABC与△AB'C'向左平移2个单位长度,使得点A与原点重合,则点C坐标为(a-2,b),∵△ABC与△AB'C'的相似比为1∶2,点A是位似中心,∴点C'的坐标为(4-2a,-2b),再将△ABC与△AB'C'向右平移2个单位长度回到原位置,则点C'的坐标为(6-2a,-2b).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十七章 相似
27.3 位似
基础过关全练
知识点1 位似图形的定义
1.(2022湖南永州宁远期末)已知△ABC∽△A'B'C',下列各选项中,△ABC与△A'B'C'不存在位似关系的是( )
2.【易错题】(2023北京海淀二模)如图,在正方形网格中,以点O为位似中心,△ABC的位似图形可以是( )
A.△DEF B.△DHF C.△GEH D.△GDH
3.(2023河北衡水二模)如图,已知△ABC与△DEF位似,且相似比为k.
(1)k= ;
(2)位似中心的坐标为 .
4.如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,AD与BE相交于点O,图中的三角形是位似图形的为 .(至少写出两对)
知识点2 位似图形的性质
5.(2022山东滨州博兴期末)如图,以点O为位似中心,把△ABC各边放大到原来的2倍得到△A'B'C'.下列说法错误的是( )
A.△ABC∽△A'B'C' B.AO∶AA'=1∶2
C.AB∥A'B' D.直线CC'经过点O
6.(2022四川成都青白江月考)如图,在△ABC所在平面上任意取一点O(与A,B,C不重合),连接OA、OB、OC,分别取OA、OB、OC的中点A1、B1、C1,再连接A1B1、A1C1、B1C1得到△A1B1C1,则下列说法不正确的是( )
A.△ABC与△A1B1C1是位似图形
B.△ABC与△A1B1C1是相似图形
C.△ABC与△A1B1C1的周长比为2∶1
D.△ABC与△A1B1C1的面积比为2∶1
7.【中华优秀传统文化】(2023山东枣庄山亭期末)《墨子·天志》记载:“轮匠执其规、矩,以度天下之方圆.”度方知圆,感悟数学之美.如图,正方形ABCD的面积为1,以它的对角线的交点为位似中心,作它的位似图形A'B'C'D',若AB∶A'B'=1∶2,则正方形A'B'C'D'的周长为 .
知识点3 位似图形的画法
8.如图,已知五边形ABCDE,试把它的边缩小为原来的,你能用几种方法 尽可能地用不同方法画图.
9.(2023安徽马鞍山花山二模)如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC的顶点均为格点(网格线的交点).
(1)将△ABC向上平移6个单位,再向右平移3个单位后得到△A1B1C1,请在网格中画出△A1B1C1;
(2)以点O为位似中心,将△ABC各边放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
知识点4 位似变换与坐标
10.(2022湖南长沙天心模拟)如图,在平面直角坐标系中,已知A(2,0),B(4,3),D(5,0),△ABC与△DEF位似,原点O是位似中心,则E点的坐标是( )
A.(10,7)
B.(8,7)
C.(10,7.5)
D.(8,6)
11.(2020黑龙江绥化中考)在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是 .
12.(2022广西河池中考)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).
(1)画出与△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,在第三象限内画一个△A2B2C2,使它与△ABC的相似比为2∶1,并写出点B2的坐标.
能力提升全练
13.(2023四川遂宁中考,6,★☆☆)在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC、△DEF成位似关系,则位似中心的坐标为( )
A.(-1,0) B.(0,0) C.(0,1) D.(1,0)
14.(2020河北中考,8,★★☆)在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
15.【易错题】(2022山东青岛市北二模,6,★★☆)如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(-2,3),先将△ABC绕点(-1,0)顺时针旋转90°得到△A1B1C1,再以原点为位似中心作△A1B1C1的位似图形△A2B2C2,若△A1B1C1与△A2B2C2的相似比为1∶2,则点A2的坐标是( )
A.(4,2) B.(6,4)
C.(6,4)或(-6,-4) D.(4,2)或(-4,-2)
16.(2022广西河池罗城模拟,16,★★☆)如图,点A是反比例函数y=(x<0)图象上的一点,直线AD分别与x轴,y轴交于点D和C,AB⊥y轴于点B,则△ABC与△DOC是以点C为位似中心的位似图形,若△ABC与△DOC的相似比为1∶3,△ABC的面积为,则k的值为 .
17.(2023海南海口期末,19,★★☆)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2)
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似图形△OA1B1,使它与△OAB的相似比为2∶1,并写出点A的对应点A1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2,并写出点A2的坐标;
(3)判断△OA1B1与△O2A2B2能否是关于某一点M为位似中心的位似图形,若能,请在图中标出位似中心M,并写出点M的坐标.
素养探究全练
18.【运算能力】(2023湖北黄冈浠水一模)如图,AB和A'B'都与x轴垂直,A点的坐标是(2,4),△AOB和△A'OB'是位似三角形,且相似比是1∶3,点C是OA'的中点,反比例函数y=(x>0)的图象经过点C,与A'B'交于点D.则点D坐标为 .
19.【推理能力】【一题多解】(2023黑龙江绥化中考)如图,在平面直角坐标系中,△ABC与△AB'C'是以点A为位似中心的位似图形,相似比为1∶2,已知点A(2,0),点C(a,b),∠C=90°,则点C'的坐标为 .(结果用含a,b的式子表示)
答案全解全析
基础过关全练
1.D 选项D中两个三角形虽然是相似三角形,但对应边BC与B'C'不平行,不是位似图形.
故选D.
2.C 如图,∵△ABC与△GEH是相似图形,而且对应顶点的连线相交于点O,对应边互相平行,∴△ABC与△GEH是以O为位似中心的位似图形.
故选C.
易错点 未根据定义作对应顶点的连线而错选.
3.(1) (2)(3,6)
解析 (1)AB=2,BC=.
(2)如图所示:
位似中心的坐标为(3,6).
4.△ABP与△DCP,△ABE与△CQE(答案不唯一)
解析 ∵在等边△ABC和等边△CDE中,∠BAC=∠ACB=∠DCE=∠DEC=60°,∴AB∥CD,BC∥DE,∴△ABP∽△DCP,又∵△ABP与△DCP对应顶点的连线相交于点P,∴△ABP与△DCP是位似图形.同理,位似图形还有△ABE与△CQE,△ACP与△AED,△BCQ与△EDQ,△BPO与△EDO,△ABO与△DQO.此外,由题意可得△ABC和△CDE也是位似图形.
5.B ∵以点O为位似中心,把△ABC各边放大到原来的2倍得到△A'B'C',∴△ABC∽△A'B'C',AB∥A'B',直线CC'经过点O,AO∶AA'=1∶3,故A、C、D选项说法正确,不符合题意;B选项说法错误,符合题意.故选B.
6.D ∵点A1、B1、C1分别是OA、OB、OC的中点,∴A1B1∥AB,A1C1∥AC,B1C1∥BC,A1B1=BC,∴△ABC与△A1B1C1是位似图形,A正确;△ABC与△A1B1C1是相似图形,B正确;△ABC与△A1B1C1的周长比为2∶1,C正确;△ABC与△A1B1C1的面积比为4∶1,D错误.故选D.
7.8
解析 ∵正方形ABCD的面积为1,∴AB=1,∴正方形ABCD的周长为4.∵AB∶A'B'=1∶2,∴,∴正方形A'B'C'D'的周长=2×4=8.
8.解析 方法一:在五边形ABCDE的外部任取一点O,
连接OA,OB,OC,OD,OE;
分别取OA,OB,OC,OD,OE的中点A',B',C',D',E',
顺次连接A',B',C',D',E',A',
即得五边形A'B'C'D'E',如图.
方法二:在五边形ABCDE的外部任取一点O,
作射线AO,BO,CO,DO,EO;
在O的另一侧取点A',B',C',D',E',
使OA'=OC,
OD'=OE,
顺次连接A',B',C',D',E',A',
即得五边形A'B'C'D'E',如图.
方法三:在五边形的内部任取一点O,
连接OA,OB,OC,OD,OE;
分别取OA,OB,OC,OD,OE的中点A',B',C',D',E',
顺次连接A',B',C',D',E',A',
即得五边形A'B'C'D'E',如图.
方法四:在AB边上取一点O,连接CO,DO,EO;
取OA,OB,OC,OD,OE的中点A',B',C',D',E',
顺次连接B',C',D',E',A',
即得五边形A'B'C'D'E',如图.
方法五:以A点为位似中心,连接AC,AD;
分别取AB,AC,AD,AE的中点B',C',D',E',
顺次连接B',C',D',E',
即得五边形AB'C'D'E',如图.
(其他方法正确亦可)
9.解析 (1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
10.C ∵△ABC与△DEF位似,原点O是位似中心,而A(2,0),D(5,0),∴△DEF与△ABC的相似比为.∵B(4,3),∴E点的坐标为,即(10,7.5).
故选C.
11.(4,8)或(-4,-8)
解析 ∵△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,又点A的坐标为(2,4),∴点A的对应点A1的坐标为(2×2,2×4)或(-2×2,-2×4),即(4,8)或(-4,-8).
12.解析 (1)如图,△A1B1C1即为所求作的图形.
(2)如图,△A2B2C2即为所求作的图形,点B2的坐标为(-4,-6).
能力提升全练
13.A 如图,△ABC与△DEF的对应顶点的连线相交于点(-1,0),则位似中心的坐标为(-1,0).故选A.
14.A 观察图形或通过计算可知四边形ABCD是菱形,选项中,四边形NPMQ是菱形,另外三个四边形不是菱形,所以,以点O为位似中心,四边形ABCD的位似图形只能是四边形NPMQ.故选A.
15.D 如图,设点P的坐标为(-1,0),连接AP、A1P,过点A作AD⊥x轴于D,过点A1作A1E⊥x轴于E,
∵∠DAP+∠APD=90°,∠EPA1+∠APD=90°,
∴∠DAP=∠EPA1,
在△DAP和△EPA1中,
∴△DAP≌△EPA1(AAS),
∴A1E=DP=1,PE=AD=3,∴点A1的坐标为(2,1),
∵△A1B1C1与△A2B2C2是以原点为位似中心的位似图形,相似比为1∶2,
∴点A2的坐标是(4,2)或(-4,-2).故选D.
易错点 易忽视乘-k的情况(k为相似比).
16.-6
解析 如图,连接OA,∵△ABC与△DOC的相似比为1∶3,∴,∵S△ABC=,∴S△ABO=3,∴=3,∵k<0,∴k=-6.
17.解析 (1)如图,△OA1B1即为所求作的图形,A1(4,2).
(2)如图,△O2A2B2即为所求作的图形,A2(0,2).
(3)△OA1B1与△O2A2B2是关于点M(-4,2)为位似中心的位似图形.
素养探究全练
18.(6,3)
解析 ∵△AOB和△A'OB'是位似三角形,且相似比是1∶3,∴.∵点A的坐标是(2,4),∴OB=2,AB=4,∴,∴A'B'=12,OB'=6,∴A'(6,12).∵点C是OA'的中点,∴C(3,6),∴k=3×6=18,即反比例函数为y=.∵A'B'⊥x轴,∴xD=xA'=6,∴yD==3,即D(6,3).
19.(6-2a,-2b)
解析 解法一:过C作CM⊥AB于M,过C'作C'N⊥AB'于N,则∠ANC'=∠AMC=90°,∵△ABC与△AB'C'的相似比为1∶2,∴,∵∠NAC'=∠CAM,∴△ACM∽△AC'N,∴,∵点A(2,0),点C(a,b),∴OA=2,OM=a,CM=b,∴AM=a-2,∴,∴AN=2a-4,C'N=2b,∴ON=AN-OA=2a-6,∴点C'的坐标为(6-2a,-2b).
解法二(巧解):将△ABC与△AB'C'向左平移2个单位长度,使得点A与原点重合,则点C坐标为(a-2,b),∵△ABC与△AB'C'的相似比为1∶2,点A是位似中心,∴点C'的坐标为(4-2a,-2b),再将△ABC与△AB'C'向右平移2个单位长度回到原位置,则点C'的坐标为(6-2a,-2b).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
