28.2.2.1 仰角、俯角,方向角课时练(含解析)
文档属性
| 名称 | 28.2.2.1 仰角、俯角,方向角课时练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 408.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:07:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第1课时 仰角、俯角,方向角
基础过关全练
知识点1 解直角三角形的应用——仰角、俯角问题
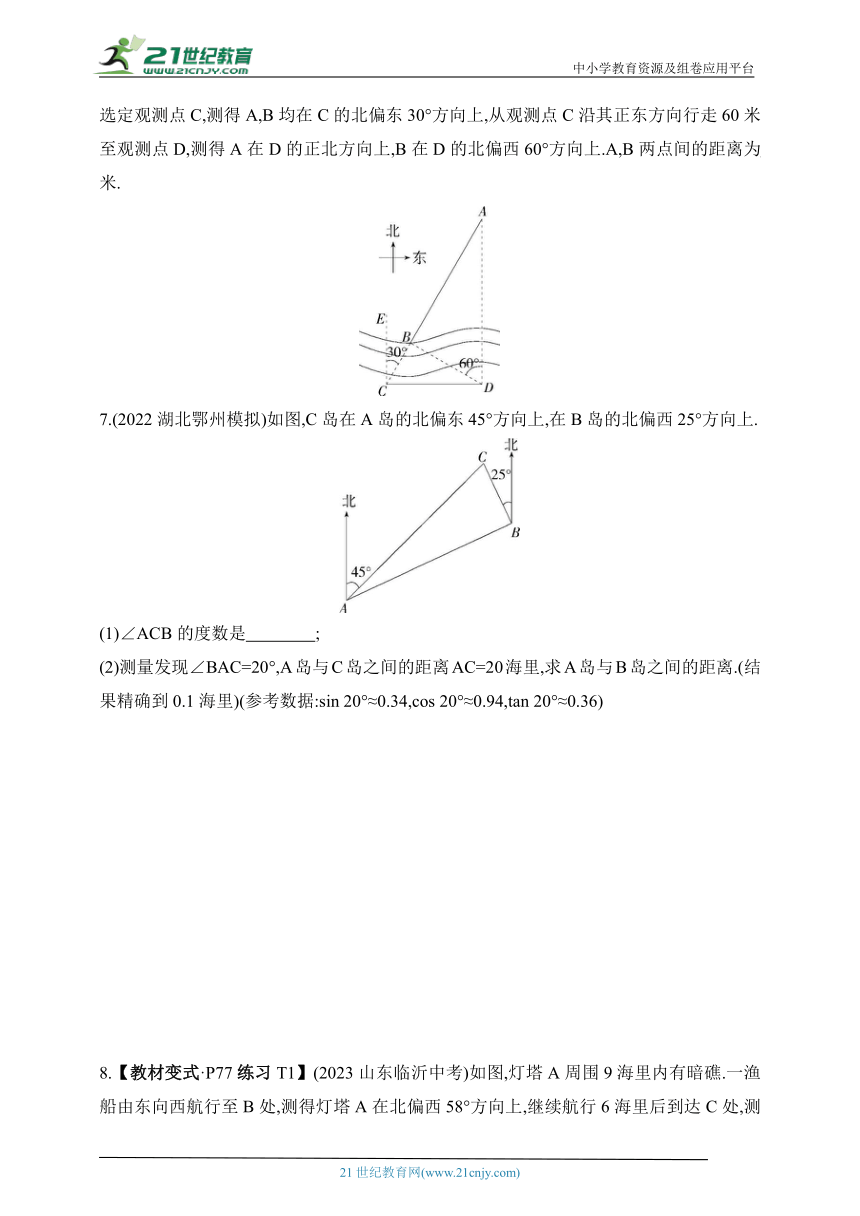
1.(2023福建宁德蕉城三模)如图,一枚运载火箭从地面L处发射,雷达站R与发射点L的距离为6 km,当火箭到达A点时,雷达站测得仰角为43°,则这枚火箭此时的高度AL为( )
A.6sin 43° km
B.6cos 43° km
C. km
D.6tan 43° km
2.(2023四川南充模拟)某数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为37米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度为( )
A.15米 B.(37-15)米
C.(45-15)米 D.22.5米
3.【教材变式·P75例4】(2022广西河池中考)如图,小敏在数学实践活动中,利用所学知识对她所在小区居民楼AB的高度进行测量,从小敏家阳台C测得点A的仰角为33°,测得点B的俯角为45°,已知观测点到地面的高度CD=36 m,求居民楼AB的高度(结果保留整数.参考数据:sin 33°≈0.54,cos 33°≈0.84,tan 33°≈0.65).
4.【国防教育】(2023河南郑州二七模拟)缅怀先烈,牢记历史,某校团委组织新入团的同学参观“二七纪念塔”,小亮在C处观察塔的顶端A的仰角为48°,向前走了26米到达D处时,测得塔的顶端A的仰角为64°,你能求出“二七纪念塔”的高度AB吗 结果精确到0.1米.参考数据:sin 48°≈,tan 48°≈,sin 64°≈,tan 64°≈2
知识点2 解直角三角形的应用——方向角问题
5.(2023河北沧州任丘模拟)如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,若海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB是( )
A. 海里
B.2sin 55° 海里
C. 海里
D.2cos 55° 海里
6.(2023广东惠州一模)如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东30°方向上,从观测点C沿其正东方向行走60米至观测点D,测得A在D的正北方向上,B在D的北偏西60°方向上.A,B两点间的距离为 米.
7.(2022湖北鄂州模拟)如图,C岛在A岛的北偏东45°方向上,在B岛的北偏西25°方向上.
(1)∠ACB的度数是 ;
(2)测量发现∠BAC=20°,A岛与C岛之间的距离AC=20海里,求A岛与B岛之间的距离.(结果精确到0.1海里)(参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36)
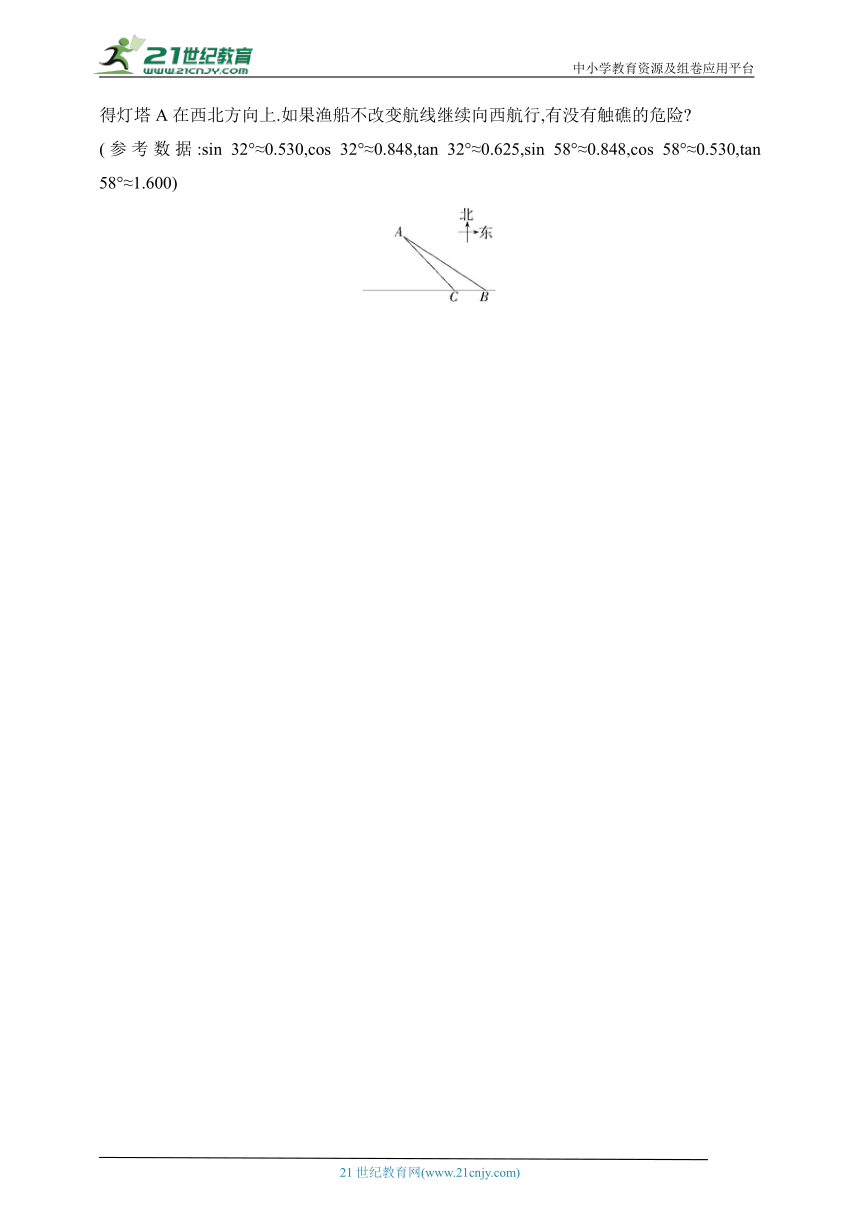
8.【教材变式·P77练习T1】(2023山东临沂中考)如图,灯塔A周围9海里内有暗礁.一渔船由东向西航行至B处,测得灯塔A在北偏西58°方向上,继续航行6海里后到达C处,测得灯塔A在西北方向上.如果渔船不改变航线继续向西航行,有没有触礁的危险
(参考数据:sin 32°≈0.530,cos 32°≈0.848,tan 32°≈0.625,sin 58°≈0.848,cos 58°≈0.530,tan 58°≈1.600)
答案全解全析
基础过关全练
D 在Rt△ALR中,RL=6 km,∠ARL=43°,tan∠ARL=,
∴AL=LR·tan∠ARL=6tan 43°km.
故选D.
B 如图,设旗杆底部为点A,顶部为点B,无人机处于点C,延长AB,交过点C的水平线于点D,由题意,得AD=37米,CD=45米,
∠DCB=30°,在Rt△BCD中,tan 30°=,
解得BD=15米,∴AB=AD-BD=(37-15)米.
故选B.
3.解析 如图,过点C作CE⊥AB于E,
由题知CD=36 m,∠BCE=45°,∠ACE=33°.
在Rt△BCE中,∠BCE=45°,
∴BE=CE=CD=36 m.
在Rt△ACE中,∠ACE=33°,CE=36 m,
∴AE=CE·tan 33°≈23.4(m),
∴AB=AE+BE=23.4+36=59.4≈59(m).
答:居民楼AB的高度约为59 m.
4.解析 由题意可得,∠ABC=90°,CD=26米,∠C=48°,∠ADB=64°,
∵tan C=,tan∠ADB=,
∴AB=CB·tan C,AB=(CB-CD)·tan∠ADB,
∴CB·tan C=(CB-CD)·tan∠ADB,
∴CB·tan 48°=(CB-26)·tan 64°,
解得CB= 米,
∴AB=·tan 48°≈≈63.6(米).
答:“二七纪念塔”的高度AB约是63.6米.
5.D 由题意,得AB⊥BP,QP∥AB,∠QPA=55°,∴∠A=∠QPA=55°,在Rt△APB中,AP=2海里,∴AB=AP·cos 55°=2cos 55°(海里),∴海轮航行的距离AB是2cos 55° 海里.故选D.
6.90
解析 由题意,得CD=60米,AD⊥CD,EC∥AD,∴∠A=∠ACE=30°,
∵∠BDA=60°,∴∠ABD=180°-∠A-∠BDA=90°.
在Rt△ACD中,AD=(米),
在Rt△ABD中,AB=AD·sin 60°=60=90(米),
∴A,B两点间的距离为90米.
7.解析 (1)∠ACB=70°.
理由:如图,过点C作CD∥AM,则∠ACD=∠MAC=45°,
由题意得AM∥BN,
∴CD∥BN,
∴∠BCD=∠CBN=25°,
∴∠ACB=∠ACD+∠BCD=70°.
(2)∵∠BAC=20°,∠ACB=70°,
∴∠ABC=180°-∠ACB-∠BAC=90°,
在Rt△ABC中,AC=20海里,
∴AB=AC·cos 20°≈20×0.94=18.8(海里),
∴A岛与B岛之间的距离约为18.8海里.
8.解析 如图,过点A作AD⊥BC交直线BC于D,
设AD=x海里,
由题意得,∠ABD=90°-58°=32°,∠ACD=45°,BC=6海里,
在Rt△ACD中,∠ACD=∠CAD=45°,
∴CD=AD=x海里,
在Rt△ABD中,tan∠ABD=,
∴BD=,即6+x≈,∴x≈10.
∵10>9,
∴如果渔船不改变航线继续向西航行,没有触礁危险.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第1课时 仰角、俯角,方向角
基础过关全练
知识点1 解直角三角形的应用——仰角、俯角问题
1.(2023福建宁德蕉城三模)如图,一枚运载火箭从地面L处发射,雷达站R与发射点L的距离为6 km,当火箭到达A点时,雷达站测得仰角为43°,则这枚火箭此时的高度AL为( )
A.6sin 43° km
B.6cos 43° km
C. km
D.6tan 43° km
2.(2023四川南充模拟)某数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为37米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度为( )
A.15米 B.(37-15)米
C.(45-15)米 D.22.5米
3.【教材变式·P75例4】(2022广西河池中考)如图,小敏在数学实践活动中,利用所学知识对她所在小区居民楼AB的高度进行测量,从小敏家阳台C测得点A的仰角为33°,测得点B的俯角为45°,已知观测点到地面的高度CD=36 m,求居民楼AB的高度(结果保留整数.参考数据:sin 33°≈0.54,cos 33°≈0.84,tan 33°≈0.65).
4.【国防教育】(2023河南郑州二七模拟)缅怀先烈,牢记历史,某校团委组织新入团的同学参观“二七纪念塔”,小亮在C处观察塔的顶端A的仰角为48°,向前走了26米到达D处时,测得塔的顶端A的仰角为64°,你能求出“二七纪念塔”的高度AB吗 结果精确到0.1米.参考数据:sin 48°≈,tan 48°≈,sin 64°≈,tan 64°≈2
知识点2 解直角三角形的应用——方向角问题
5.(2023河北沧州任丘模拟)如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A处,若海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB是( )
A. 海里
B.2sin 55° 海里
C. 海里
D.2cos 55° 海里
6.(2023广东惠州一模)如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东30°方向上,从观测点C沿其正东方向行走60米至观测点D,测得A在D的正北方向上,B在D的北偏西60°方向上.A,B两点间的距离为 米.
7.(2022湖北鄂州模拟)如图,C岛在A岛的北偏东45°方向上,在B岛的北偏西25°方向上.
(1)∠ACB的度数是 ;
(2)测量发现∠BAC=20°,A岛与C岛之间的距离AC=20海里,求A岛与B岛之间的距离.(结果精确到0.1海里)(参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36)
8.【教材变式·P77练习T1】(2023山东临沂中考)如图,灯塔A周围9海里内有暗礁.一渔船由东向西航行至B处,测得灯塔A在北偏西58°方向上,继续航行6海里后到达C处,测得灯塔A在西北方向上.如果渔船不改变航线继续向西航行,有没有触礁的危险
(参考数据:sin 32°≈0.530,cos 32°≈0.848,tan 32°≈0.625,sin 58°≈0.848,cos 58°≈0.530,tan 58°≈1.600)
答案全解全析
基础过关全练
D 在Rt△ALR中,RL=6 km,∠ARL=43°,tan∠ARL=,
∴AL=LR·tan∠ARL=6tan 43°km.
故选D.
B 如图,设旗杆底部为点A,顶部为点B,无人机处于点C,延长AB,交过点C的水平线于点D,由题意,得AD=37米,CD=45米,
∠DCB=30°,在Rt△BCD中,tan 30°=,
解得BD=15米,∴AB=AD-BD=(37-15)米.
故选B.
3.解析 如图,过点C作CE⊥AB于E,
由题知CD=36 m,∠BCE=45°,∠ACE=33°.
在Rt△BCE中,∠BCE=45°,
∴BE=CE=CD=36 m.
在Rt△ACE中,∠ACE=33°,CE=36 m,
∴AE=CE·tan 33°≈23.4(m),
∴AB=AE+BE=23.4+36=59.4≈59(m).
答:居民楼AB的高度约为59 m.
4.解析 由题意可得,∠ABC=90°,CD=26米,∠C=48°,∠ADB=64°,
∵tan C=,tan∠ADB=,
∴AB=CB·tan C,AB=(CB-CD)·tan∠ADB,
∴CB·tan C=(CB-CD)·tan∠ADB,
∴CB·tan 48°=(CB-26)·tan 64°,
解得CB= 米,
∴AB=·tan 48°≈≈63.6(米).
答:“二七纪念塔”的高度AB约是63.6米.
5.D 由题意,得AB⊥BP,QP∥AB,∠QPA=55°,∴∠A=∠QPA=55°,在Rt△APB中,AP=2海里,∴AB=AP·cos 55°=2cos 55°(海里),∴海轮航行的距离AB是2cos 55° 海里.故选D.
6.90
解析 由题意,得CD=60米,AD⊥CD,EC∥AD,∴∠A=∠ACE=30°,
∵∠BDA=60°,∴∠ABD=180°-∠A-∠BDA=90°.
在Rt△ACD中,AD=(米),
在Rt△ABD中,AB=AD·sin 60°=60=90(米),
∴A,B两点间的距离为90米.
7.解析 (1)∠ACB=70°.
理由:如图,过点C作CD∥AM,则∠ACD=∠MAC=45°,
由题意得AM∥BN,
∴CD∥BN,
∴∠BCD=∠CBN=25°,
∴∠ACB=∠ACD+∠BCD=70°.
(2)∵∠BAC=20°,∠ACB=70°,
∴∠ABC=180°-∠ACB-∠BAC=90°,
在Rt△ABC中,AC=20海里,
∴AB=AC·cos 20°≈20×0.94=18.8(海里),
∴A岛与B岛之间的距离约为18.8海里.
8.解析 如图,过点A作AD⊥BC交直线BC于D,
设AD=x海里,
由题意得,∠ABD=90°-58°=32°,∠ACD=45°,BC=6海里,
在Rt△ACD中,∠ACD=∠CAD=45°,
∴CD=AD=x海里,
在Rt△ABD中,tan∠ABD=,
∴BD=,即6+x≈,∴x≈10.
∵10>9,
∴如果渔船不改变航线继续向西航行,没有触礁危险.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
