28.2.2.2 坡度、坡角,实际生活问题课时练(含解析)
文档属性
| 名称 | 28.2.2.2 坡度、坡角,实际生活问题课时练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 746.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:08:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第2课时 坡度、坡角,实际生活问题
基础过关全练
知识点3 解直角三角形的应用——坡度、坡角问题
9.(2022湖南邵阳模拟)如图,拦水坝的横断面为梯形ABCD,其中AD∥BC,迎水坡AB的坡角∠ABC=45°,背水坡CD的坡比为1∶,迎水坡AB的长为8 m,则背水坡CD的长为( )
A.6 m B.8 m C.4 m D.8 m
10.(2023广东汕头金平三模)如图,斜坡AB的坡度i1=1∶,现需要在不改变坡高AH的前提下将坡度变缓,调整后的斜坡AC的坡度i2=1∶2.4,已知斜坡AB=10米,那么斜坡AC= 米.
11.(2023四川绵阳游仙模拟)如图,某水上乐园在一平地推出了“急流勇进”的项目,项目有两条斜坡滑道(BC、AD)以满足不同的难度需求,游客可以乘坐垂直升降电梯沿AB自由上下选择项目难度.其中斜坡滑道BC的坡度为i=5∶12,BC=13米,CD=16米,∠D=32°(其中点A、B、C、D均在同一平面内),则垂直升降电梯的升降高度AB约为 米.(参考数据:sin 32°≈0.530,cos 32°≈0.848,tan 32°≈0.625)
(2022湖南株洲中考)如图1所示,某登山运动爱好者由山坡①的点A处沿线段AC行至山谷点C处,再从点C处沿线段CB行至山坡②的点B处.
如图2所示,将直线l视为水平面,山坡①的坡角∠ACM=30°,AM=0.6千米,山坡②的坡度i=1∶1,BN⊥l于N,且CN=千米.
(1)求∠ACB的度数;
(2)求在此过程中该登山运动爱好者走过的路程.
知识点4 解直角三角形在其他实际问题中的应用
13.(2022福建中考)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44 cm,则高AD约为(参考数据:sin 27°≈0.45,cos 27°≈0.89,tan 27°≈0.51)( )
A.9.90 cm B.11.22 cm
C.19.58 cm D.22.44 cm
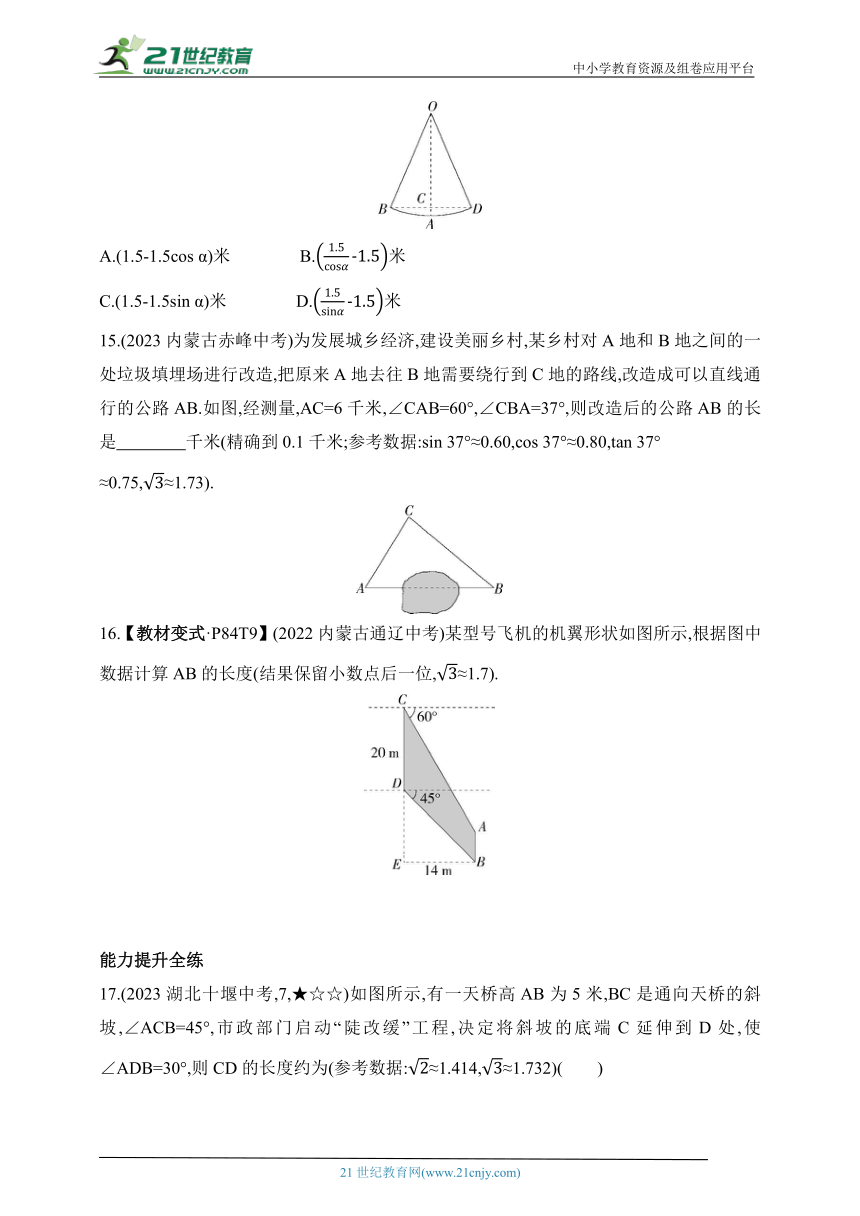
14.(2023河南郑州金水二模)如图,一个钟摆的摆长OB为1.5米,当钟摆向两边摆动时,摆角∠BOD为2α,且两边的摆动角度相同,则它摆至的最高位置与最低位置的高度之差AC为( )
A.(1.5-1.5cos α)米 B.米
C.(1.5-1.5sin α)米 D.米
15.(2023内蒙古赤峰中考)为发展城乡经济,建设美丽乡村,某乡村对A地和B地之间的一处垃圾填埋场进行改造,把原来A地去往B地需要绕行到C地的路线,改造成可以直线通行的公路AB.如图,经测量,AC=6千米,∠CAB=60°,∠CBA=37°,则改造后的公路AB的长是 千米(精确到0.1千米;参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°
≈0.75,≈1.73).
16.【教材变式·P84T9】(2022内蒙古通辽中考)某型号飞机的机翼形状如图所示,根据图中数据计算AB的长度(结果保留小数点后一位,≈1.7).
能力提升全练
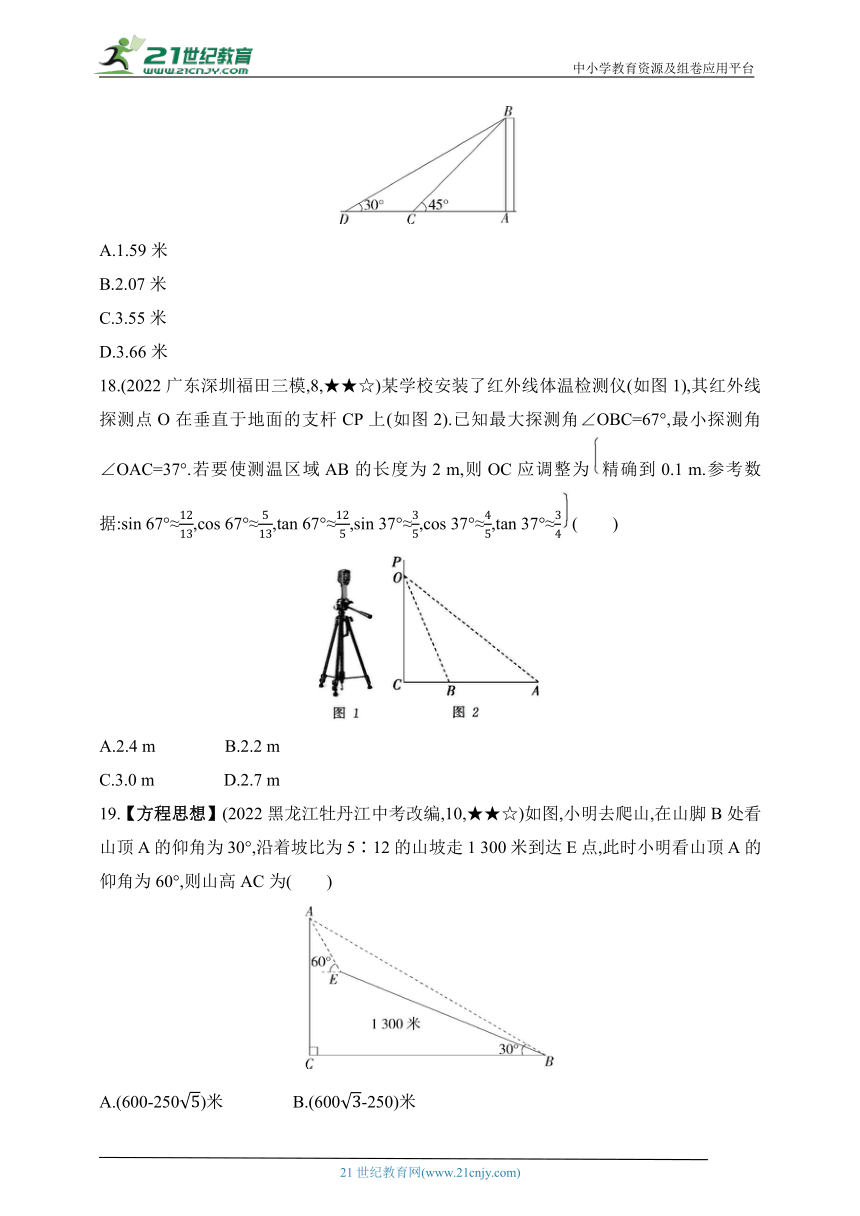
17.(2023湖北十堰中考,7,★☆☆)如图所示,有一天桥高AB为5米,BC是通向天桥的斜坡,∠ACB=45°,市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使∠ADB=30°,则CD的长度约为(参考数据:≈1.414,≈1.732)( )
A.1.59米
B.2.07米
C.3.55米
D.3.66米
18.(2022广东深圳福田三模,8,★★☆)某学校安装了红外线体温检测仪(如图1),其红外线探测点O在垂直于地面的支杆CP上(如图2).已知最大探测角∠OBC=67°,最小探测角∠OAC=37°.若要使测温区域AB的长度为2 m,则OC应调整为精确到0.1 m.参考数据:sin 67°≈,cos 67°≈,tan 67°≈,sin 37°≈,cos 37°≈,tan 37°≈( )
A.2.4 m B.2.2 m
C.3.0 m D.2.7 m
19.【方程思想】(2022黑龙江牡丹江中考改编,10,★★☆)如图,小明去爬山,在山脚B处看山顶A的仰角为30°,沿着坡比为5∶12的山坡走1 300米到达E点,此时小明看山顶A的仰角为60°,则山高AC为( )
A.(600-250)米 B.(600-250)米
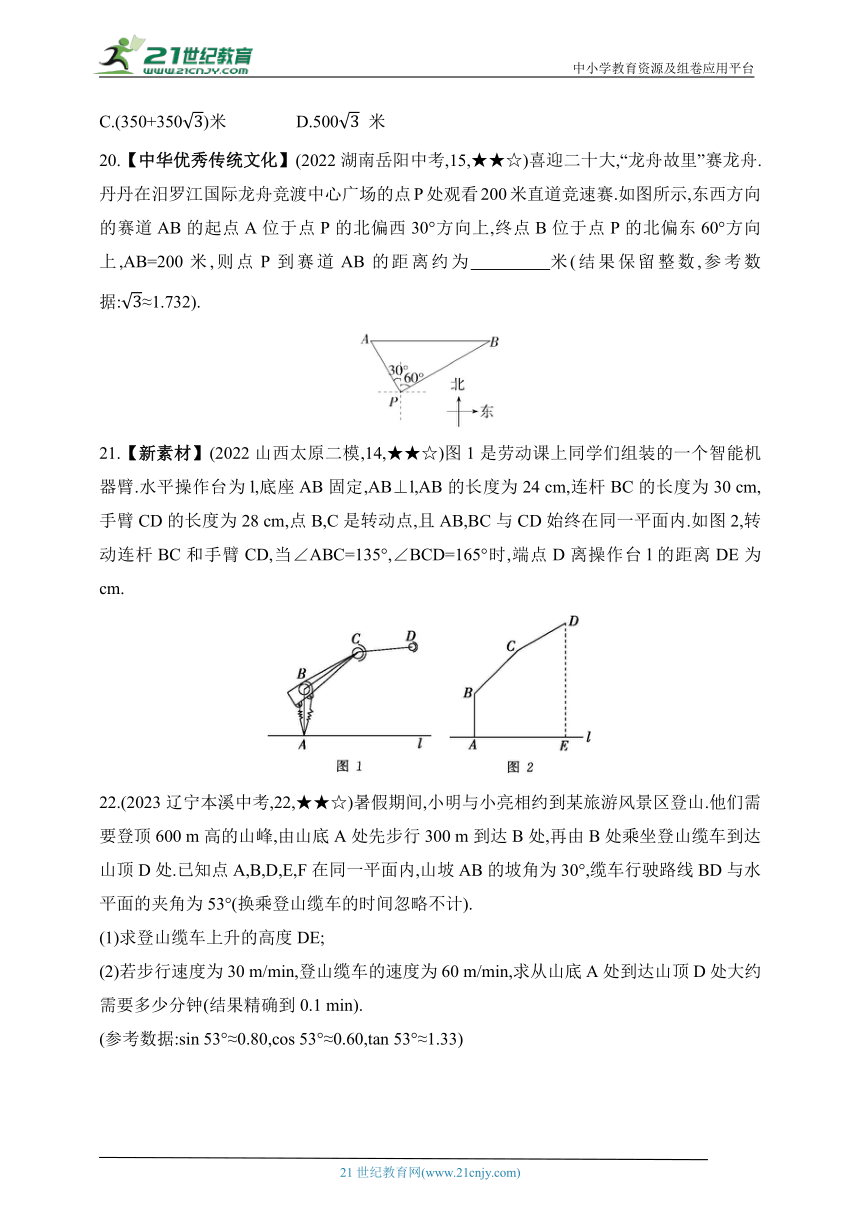
C.(350+350)米 D.500 米
20.【中华优秀传统文化】(2022湖南岳阳中考,15,★★☆)喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场的点P处观看200米直道竞速赛.如图所示,东西方向的赛道AB的起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=200米,则点P到赛道AB的距离约为 米(结果保留整数,参考数据:≈1.732).
21.【新素材】(2022山西太原二模,14,★★☆)图1是劳动课上同学们组装的一个智能机器臂.水平操作台为l,底座AB固定,AB⊥l,AB的长度为24 cm,连杆BC的长度为30 cm,手臂CD的长度为28 cm,点B,C是转动点,且AB,BC与CD始终在同一平面内.如图2,转动连杆BC和手臂CD,当∠ABC=135°,∠BCD=165°时,端点D离操作台l的距离DE为 cm.
22.(2023辽宁本溪中考,22,★★☆)暑假期间,小明与小亮相约到某旅游风景区登山.他们需要登顶600 m高的山峰,由山底A处先步行300 m到达B处,再由B处乘坐登山缆车到达山顶D处.已知点A,B,D,E,F在同一平面内,山坡AB的坡角为30°,缆车行驶路线BD与水平面的夹角为53°(换乘登山缆车的时间忽略不计).
(1)求登山缆车上升的高度DE;
(2)若步行速度为30 m/min,登山缆车的速度为60 m/min,求从山底A处到达山顶D处大约需要多少分钟(结果精确到0.1 min).
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33)
23.【真实情境】(2023浙江嘉兴中考,22,★★☆)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度OA=160 cm,识别的最远水平距离OB=150 cm.
(1)身高208 cm的小杜,头部高度为26 cm,他站在离摄像头水平距离130 cm的点C处,那么小杜最少需要下蹲多少厘米才能被识别
(2)身高120 cm的小若,头部高度为15 cm,踮起脚尖可以增高3 cm,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗 请计算说明.
(精确到0.1 cm,参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36)
素养探究全练
24.【应用意识】(2023四川绵阳三台模拟)
小丽测量了斜坡上一棵垂直于地面的大树的高度.如图,小丽先在坡角为30°的斜坡AB上的点A处,测得树尖E的仰角为15°,然后沿斜坡走了10米到达坡脚B处,又在水平路面上行走20米到达大树所在斜坡CD的坡脚C处,大树所在斜坡CD的坡度i=3∶4,且大树的底端与坡脚的距离CD为15米,则大树ED的高度约为 .(结果精确到0.1米.参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,≈1.73)
25.【应用意识】(2023湖南常德中考)今年“五一”小长假期间,小陈、小余和家长去沙滩公园游玩.坐在如图1所示的椅子上休息时,小陈感觉很舒服,这激发了她对这把椅子的好奇心,就想出个问题考考小余.小陈先进行测量,并根据测量结果画出了图1的示意图(如图2).在图2中,已知四边形ABCD是平行四边形,座板CD与地面MN平行,△EBC是等腰三角形且BC=CE,∠FBA=114.2°,靠背FC=57 cm,支架AN=43 cm,扶手的一部分BE=16.4 cm.这时她问小余:“你能算出靠背顶端F点距地面(MN)的高度是多少吗 ”请你帮小余算出结果(最后结果保留一位小数).(参考数据:sin 65.8°≈0.91,cos 65.8°≈0.41,tan 65.8°≈2.23)
答案全解全析
基础过关全练
9.D 如图,过点A作AF⊥BC,垂足为F,过点D作DE⊥BC,垂足为E.∵AD∥BC,∴AF=DE.在Rt△ABF中,∠ABF=45°,AB=8 m,∴AF=AB·sin 45°=8× m.在Rt△DEC中,tan∠DCE=,∴∠DCE=30°,∴CD=2DE=8(m).故选D.
10.13
解析 ∵i1=1∶,∴tan∠ABH=,∴∠ABH=30°,∴AH=×10=5(米),∵坡度i2=1∶2.4,∴,即,解得CH=12(米),∴AC==13(米).
11.12.5
解析 如图,延长AB、DC交于点E,由BC的坡度为i=5∶12,得BE∶CE=5∶12.设BE=5x米,CE=12x米,在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,即(5x)2+(12x)2=132,解得x=1(负值舍去),即BE=5米,CE=12米,∴DE=DC+CE=16+12=28(米),∵tan D=,
∴AE=DE·tan D=28tan 32°(米).
∴AB=AE-BE=28tan 32°-5≈12.5(米).
12.解析 (1)∵山坡②的坡度i=1∶1,
∴CN=BN,∴∠BCN=45°,
∴∠ACB=180°-30°-45°=105°.
(2)在Rt△ACM中,∠AMC=90°,∠ACM=30°,AM=0.6千米,∴AC=2AM=1.2千米,
在Rt△BCN中,∠BNC=90°,∠BCN=45°,CN=千米,∴BC==2(千米),
∴该登山运动爱好者走过的路程为1.2+2=3.2(千米).
答:该登山运动爱好者走过的路程为3.2千米.
13.B ∵AB=AC,BC=44 cm,AD⊥BC,∴BD=CD=22 cm.∵∠ABC=27°,∴tan∠ABC=≈0.51,∴AD≈0.51×22=11.22 cm.故选B.
14.A 由题意,得OA⊥BD,∠BOC=∠BOD=·2α=α,OB=OA=1.5米,在Rt△BOC中,OC=OB·cos α=1.5cos α米,∴AC=OA-OC=(1.5-1.5cos α)米.故选A.
15.9.9
解析 如图,过点C作CD⊥AB于点D,在Rt△ADC中,AC=6千米,
∠CAD=60°,cos∠CAD=,sin∠CAD=,
∴AD=AC·cos∠CAD=6cos 60°=3(千米),
CD=AC·sin∠CAD=6sin 60°=3(千米).
在Rt△CDB中,∠CBD=37°,CD=3千米,tan∠CBD=
(千米),
∴AB=AD+DB=3+4≈3+4×1.73≈9.9(千米),
即改造后的公路AB的长约是9.9千米.
16.解析 如图,∠BDE=90°-45°=45°,在Rt△BDE中,
DE=BE=14 m.
∵CM=BE=14 m,在Rt△ACM中,∠ACM=60°,
∴AM=(m),
∴AB=BM-AM=CE-AM=20+14-14≈10.2(m).
答:AB的长约为10.2 m.
能力提升全练
D 在Rt△ABC中,∠BAC=90°,∠ACB=45°,
∴∠ABC=∠ACB=45°,∴AC=AB=5米.
在Rt△ABD中,∠BAD=90°,∠ADB=30°,
∴∠ABD=60°,∴=tan∠ABD=tan 60°=AB-AC≈1.732×5-5=3.66(米),∴CD的长度约为3.66米.故选D.
B 设BC=x m,∵AB=2 m,∴AC=(x+2)m.
∵OC=BC·tan∠OBC=BC·tan 67°≈x m,
OC=AC·tan∠OAC=AC·tan 37°≈
(x+2),解得x=≈2.2 m.故选B.
19.B 如图,作EF垂直CB于点F,EN垂直AC于点N,∵斜坡BE的坡度为5∶12,∴设EF=5x米,则BF=12x米,由勾股定理得(5x)2+(12x)2=1 3002,解得x=100(舍负),则EF=500米,BF=1 200米.由题意可知,四边形NCFE为矩形,∴NC=EF=500米,NE=CF.在Rt△ANE中,tan∠AEN=tan 60°=,∵tan 60°=AN.在Rt△ACB中,tan∠ABC=tan 30°=,∵tan 30°=,解得AN=(600-750)米,∴山高AC=AN+NC=600-250)米,故选B.
20.87
解析 如图,过点P作PC⊥AB,垂足为C,设PC=x米,在Rt△APC中,∠APC=30°,∴AC=PC·tan 30°=x(米).在Rt△BCP中,∠CPB=60°,∴BC=CP·tan 60°=x(米).∵AB=200米,∴AC+BC=200米,∴x=200,解得x=50≈87,∴点P到赛道AB的距离约为87米.
21.(38+15)
解析 如图,过点B作BF⊥DE于F,过点C作CG⊥BF于G,过点C作CH⊥DE于H,则四边形ABFE、四边形CGFH都是矩形,
∴AB=EF=24 cm,CG=HF,∠BGC=∠ABF=∠GCH=90°.
∵∠ABC=135°,∴∠CBG=∠ABC-∠ABF=45°,
∴∠BCG=90°-∠CBG=45°.
∵∠BCD=165°,∴∠DCH=∠BCD-∠BCG-∠GCH=30°.
在Rt△BCG中,BC=30 cm,∴CG=BC·sin 45°=30×
cm,在Rt△CDH中,CD=28 cm,
∴DH=CD·sin 30°=28×
)cm.
22.解析 (1)如图,过点B作BM⊥AF于点M,
由题可知,∠A=30°,∠DBE=53°,DF=600 m,AB=300 m,
在Rt△ABM中,∠A=30°,AB=300 m,
∴BM=AB=150 m,∴EF=BM=150 m,
∴DE=DF-EF=600-150=450(m).
答:登山缆车上升的高度DE为450 m.
(2)在Rt△BDE中,∠DBE=53°,DE=450 m,
∴BD==562.5(m),
∴需要的时间=步行时间+乘坐缆车时间=≈19.4(min).
答:从山底A处到达山顶D处大约需要19.4分钟.
23.解析 (1)如图,过C作OB的垂线分别交仰角线、俯角线于点E、D,交水平线于点F,
在Rt△AEF中,tan∠EAF=,
∴EF=AF·tan 15°≈130×0.27=35.1(cm),
∴CE=CF+EF=160+35.1=195.1(cm),
∴小杜最少需要下蹲208-195.1=12.9厘米才能被识别.
(2)小若能被识别.
理由:如图,过B作OB的垂线分别交仰角线、俯角线于M、N,交水平线于P,
在Rt△APM中,tan∠MAP=,
∴MP=AP·tan 20°≈150×0.36=54.0(cm),
∵∠MAP=∠NAP,AP=AP,∠APM=∠APN=90°,
∴△AMP≌△ANP(ASA),∴PN=MP=54.0 cm,
∴BN=160-54.0=106.0(cm),
∵120-15=105(cm),106.0 cm>105 cm,
∴小若必须踮起脚尖.
∵小若踮起脚尖后头顶距地面的高度为120+3=123(cm),
∴小若踮起脚尖后头顶超出点N的高度为123-106.0=17.0(cm)>15 cm,
∴小若能被识别.
素养探究全练
24.7.0米
解析 如图,延长BC、ED相交于点F,过点A作AG⊥EF,垂足为G,过点A作AH⊥CB,交CB的延长线于点H.
由题意,得AH=FG,AG=HF,BC=20米,EF⊥BF,
在Rt△ABH中,∠ABH=30°,AB=10米,
∴AH=AB=5(米),BH=(米),
∴GF=AH=5米.
∵斜坡CD的坡度i=3∶4,∴,∴设DF=3x米,则CF=4x米,
在Rt△CDF中,CD==5x(米),
∵CD=15米,∴5x=15,解得x=3,∴CF=12米,DF=9米,
∴AG=HF=BH+BC+CF=(32+5)米,在Rt△AGE中,∠EAG=15°,
∴EG=AG·tan 15°≈(32+5)×0.27≈10.98(米),
∴ED=EG+FG-DF=10.98+5-9≈7.0(米),∴大树ED的高度约为7.0米.
25.解析 如图,过点F作FQ⊥CD交直线CD于点Q,过点A作AP⊥MN于点P,过点C作CH⊥AB于点H.
∵四边形ABCD是平行四边形,∠FBA=114.2°,
∴∠FCQ=∠CBA=180°-114.2°=65.8°,
∴FQ=FC·sin∠FCQ=57sin 65.8° cm.
由题意知AB∥CD∥MN,FC∥AN,
则∠ANP=∠ADC=∠FCQ=65.8°,又AN=43 cm,
∴AP=AN·sin∠ANP=43sin 65.8° cm.
∵BC=CE,EB=16.4 cm,∴BH=8.2 cm,
∴CH=BH·tan∠CBH=8.2×tan 65.8°≈8.2×2.23≈18.29 cm,
∴靠背顶端F点距地面(MN)的高度为
FQ+AP-CH=57sin 65.8°+43sin 65.8°-18.29≈100×0.91-18.29=72.71
≈72.7 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.2 应用举例
第2课时 坡度、坡角,实际生活问题
基础过关全练
知识点3 解直角三角形的应用——坡度、坡角问题
9.(2022湖南邵阳模拟)如图,拦水坝的横断面为梯形ABCD,其中AD∥BC,迎水坡AB的坡角∠ABC=45°,背水坡CD的坡比为1∶,迎水坡AB的长为8 m,则背水坡CD的长为( )
A.6 m B.8 m C.4 m D.8 m
10.(2023广东汕头金平三模)如图,斜坡AB的坡度i1=1∶,现需要在不改变坡高AH的前提下将坡度变缓,调整后的斜坡AC的坡度i2=1∶2.4,已知斜坡AB=10米,那么斜坡AC= 米.
11.(2023四川绵阳游仙模拟)如图,某水上乐园在一平地推出了“急流勇进”的项目,项目有两条斜坡滑道(BC、AD)以满足不同的难度需求,游客可以乘坐垂直升降电梯沿AB自由上下选择项目难度.其中斜坡滑道BC的坡度为i=5∶12,BC=13米,CD=16米,∠D=32°(其中点A、B、C、D均在同一平面内),则垂直升降电梯的升降高度AB约为 米.(参考数据:sin 32°≈0.530,cos 32°≈0.848,tan 32°≈0.625)
(2022湖南株洲中考)如图1所示,某登山运动爱好者由山坡①的点A处沿线段AC行至山谷点C处,再从点C处沿线段CB行至山坡②的点B处.
如图2所示,将直线l视为水平面,山坡①的坡角∠ACM=30°,AM=0.6千米,山坡②的坡度i=1∶1,BN⊥l于N,且CN=千米.
(1)求∠ACB的度数;
(2)求在此过程中该登山运动爱好者走过的路程.
知识点4 解直角三角形在其他实际问题中的应用
13.(2022福建中考)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44 cm,则高AD约为(参考数据:sin 27°≈0.45,cos 27°≈0.89,tan 27°≈0.51)( )
A.9.90 cm B.11.22 cm
C.19.58 cm D.22.44 cm
14.(2023河南郑州金水二模)如图,一个钟摆的摆长OB为1.5米,当钟摆向两边摆动时,摆角∠BOD为2α,且两边的摆动角度相同,则它摆至的最高位置与最低位置的高度之差AC为( )
A.(1.5-1.5cos α)米 B.米
C.(1.5-1.5sin α)米 D.米
15.(2023内蒙古赤峰中考)为发展城乡经济,建设美丽乡村,某乡村对A地和B地之间的一处垃圾填埋场进行改造,把原来A地去往B地需要绕行到C地的路线,改造成可以直线通行的公路AB.如图,经测量,AC=6千米,∠CAB=60°,∠CBA=37°,则改造后的公路AB的长是 千米(精确到0.1千米;参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°
≈0.75,≈1.73).
16.【教材变式·P84T9】(2022内蒙古通辽中考)某型号飞机的机翼形状如图所示,根据图中数据计算AB的长度(结果保留小数点后一位,≈1.7).
能力提升全练
17.(2023湖北十堰中考,7,★☆☆)如图所示,有一天桥高AB为5米,BC是通向天桥的斜坡,∠ACB=45°,市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使∠ADB=30°,则CD的长度约为(参考数据:≈1.414,≈1.732)( )
A.1.59米
B.2.07米
C.3.55米
D.3.66米
18.(2022广东深圳福田三模,8,★★☆)某学校安装了红外线体温检测仪(如图1),其红外线探测点O在垂直于地面的支杆CP上(如图2).已知最大探测角∠OBC=67°,最小探测角∠OAC=37°.若要使测温区域AB的长度为2 m,则OC应调整为精确到0.1 m.参考数据:sin 67°≈,cos 67°≈,tan 67°≈,sin 37°≈,cos 37°≈,tan 37°≈( )
A.2.4 m B.2.2 m
C.3.0 m D.2.7 m
19.【方程思想】(2022黑龙江牡丹江中考改编,10,★★☆)如图,小明去爬山,在山脚B处看山顶A的仰角为30°,沿着坡比为5∶12的山坡走1 300米到达E点,此时小明看山顶A的仰角为60°,则山高AC为( )
A.(600-250)米 B.(600-250)米
C.(350+350)米 D.500 米
20.【中华优秀传统文化】(2022湖南岳阳中考,15,★★☆)喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场的点P处观看200米直道竞速赛.如图所示,东西方向的赛道AB的起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=200米,则点P到赛道AB的距离约为 米(结果保留整数,参考数据:≈1.732).
21.【新素材】(2022山西太原二模,14,★★☆)图1是劳动课上同学们组装的一个智能机器臂.水平操作台为l,底座AB固定,AB⊥l,AB的长度为24 cm,连杆BC的长度为30 cm,手臂CD的长度为28 cm,点B,C是转动点,且AB,BC与CD始终在同一平面内.如图2,转动连杆BC和手臂CD,当∠ABC=135°,∠BCD=165°时,端点D离操作台l的距离DE为 cm.
22.(2023辽宁本溪中考,22,★★☆)暑假期间,小明与小亮相约到某旅游风景区登山.他们需要登顶600 m高的山峰,由山底A处先步行300 m到达B处,再由B处乘坐登山缆车到达山顶D处.已知点A,B,D,E,F在同一平面内,山坡AB的坡角为30°,缆车行驶路线BD与水平面的夹角为53°(换乘登山缆车的时间忽略不计).
(1)求登山缆车上升的高度DE;
(2)若步行速度为30 m/min,登山缆车的速度为60 m/min,求从山底A处到达山顶D处大约需要多少分钟(结果精确到0.1 min).
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33)
23.【真实情境】(2023浙江嘉兴中考,22,★★☆)图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度OA=160 cm,识别的最远水平距离OB=150 cm.
(1)身高208 cm的小杜,头部高度为26 cm,他站在离摄像头水平距离130 cm的点C处,那么小杜最少需要下蹲多少厘米才能被识别
(2)身高120 cm的小若,头部高度为15 cm,踮起脚尖可以增高3 cm,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗 请计算说明.
(精确到0.1 cm,参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36)
素养探究全练
24.【应用意识】(2023四川绵阳三台模拟)
小丽测量了斜坡上一棵垂直于地面的大树的高度.如图,小丽先在坡角为30°的斜坡AB上的点A处,测得树尖E的仰角为15°,然后沿斜坡走了10米到达坡脚B处,又在水平路面上行走20米到达大树所在斜坡CD的坡脚C处,大树所在斜坡CD的坡度i=3∶4,且大树的底端与坡脚的距离CD为15米,则大树ED的高度约为 .(结果精确到0.1米.参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27,≈1.73)
25.【应用意识】(2023湖南常德中考)今年“五一”小长假期间,小陈、小余和家长去沙滩公园游玩.坐在如图1所示的椅子上休息时,小陈感觉很舒服,这激发了她对这把椅子的好奇心,就想出个问题考考小余.小陈先进行测量,并根据测量结果画出了图1的示意图(如图2).在图2中,已知四边形ABCD是平行四边形,座板CD与地面MN平行,△EBC是等腰三角形且BC=CE,∠FBA=114.2°,靠背FC=57 cm,支架AN=43 cm,扶手的一部分BE=16.4 cm.这时她问小余:“你能算出靠背顶端F点距地面(MN)的高度是多少吗 ”请你帮小余算出结果(最后结果保留一位小数).(参考数据:sin 65.8°≈0.91,cos 65.8°≈0.41,tan 65.8°≈2.23)
答案全解全析
基础过关全练
9.D 如图,过点A作AF⊥BC,垂足为F,过点D作DE⊥BC,垂足为E.∵AD∥BC,∴AF=DE.在Rt△ABF中,∠ABF=45°,AB=8 m,∴AF=AB·sin 45°=8× m.在Rt△DEC中,tan∠DCE=,∴∠DCE=30°,∴CD=2DE=8(m).故选D.
10.13
解析 ∵i1=1∶,∴tan∠ABH=,∴∠ABH=30°,∴AH=×10=5(米),∵坡度i2=1∶2.4,∴,即,解得CH=12(米),∴AC==13(米).
11.12.5
解析 如图,延长AB、DC交于点E,由BC的坡度为i=5∶12,得BE∶CE=5∶12.设BE=5x米,CE=12x米,在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,即(5x)2+(12x)2=132,解得x=1(负值舍去),即BE=5米,CE=12米,∴DE=DC+CE=16+12=28(米),∵tan D=,
∴AE=DE·tan D=28tan 32°(米).
∴AB=AE-BE=28tan 32°-5≈12.5(米).
12.解析 (1)∵山坡②的坡度i=1∶1,
∴CN=BN,∴∠BCN=45°,
∴∠ACB=180°-30°-45°=105°.
(2)在Rt△ACM中,∠AMC=90°,∠ACM=30°,AM=0.6千米,∴AC=2AM=1.2千米,
在Rt△BCN中,∠BNC=90°,∠BCN=45°,CN=千米,∴BC==2(千米),
∴该登山运动爱好者走过的路程为1.2+2=3.2(千米).
答:该登山运动爱好者走过的路程为3.2千米.
13.B ∵AB=AC,BC=44 cm,AD⊥BC,∴BD=CD=22 cm.∵∠ABC=27°,∴tan∠ABC=≈0.51,∴AD≈0.51×22=11.22 cm.故选B.
14.A 由题意,得OA⊥BD,∠BOC=∠BOD=·2α=α,OB=OA=1.5米,在Rt△BOC中,OC=OB·cos α=1.5cos α米,∴AC=OA-OC=(1.5-1.5cos α)米.故选A.
15.9.9
解析 如图,过点C作CD⊥AB于点D,在Rt△ADC中,AC=6千米,
∠CAD=60°,cos∠CAD=,sin∠CAD=,
∴AD=AC·cos∠CAD=6cos 60°=3(千米),
CD=AC·sin∠CAD=6sin 60°=3(千米).
在Rt△CDB中,∠CBD=37°,CD=3千米,tan∠CBD=
(千米),
∴AB=AD+DB=3+4≈3+4×1.73≈9.9(千米),
即改造后的公路AB的长约是9.9千米.
16.解析 如图,∠BDE=90°-45°=45°,在Rt△BDE中,
DE=BE=14 m.
∵CM=BE=14 m,在Rt△ACM中,∠ACM=60°,
∴AM=(m),
∴AB=BM-AM=CE-AM=20+14-14≈10.2(m).
答:AB的长约为10.2 m.
能力提升全练
D 在Rt△ABC中,∠BAC=90°,∠ACB=45°,
∴∠ABC=∠ACB=45°,∴AC=AB=5米.
在Rt△ABD中,∠BAD=90°,∠ADB=30°,
∴∠ABD=60°,∴=tan∠ABD=tan 60°=AB-AC≈1.732×5-5=3.66(米),∴CD的长度约为3.66米.故选D.
B 设BC=x m,∵AB=2 m,∴AC=(x+2)m.
∵OC=BC·tan∠OBC=BC·tan 67°≈x m,
OC=AC·tan∠OAC=AC·tan 37°≈
(x+2),解得x=≈2.2 m.故选B.
19.B 如图,作EF垂直CB于点F,EN垂直AC于点N,∵斜坡BE的坡度为5∶12,∴设EF=5x米,则BF=12x米,由勾股定理得(5x)2+(12x)2=1 3002,解得x=100(舍负),则EF=500米,BF=1 200米.由题意可知,四边形NCFE为矩形,∴NC=EF=500米,NE=CF.在Rt△ANE中,tan∠AEN=tan 60°=,∵tan 60°=AN.在Rt△ACB中,tan∠ABC=tan 30°=,∵tan 30°=,解得AN=(600-750)米,∴山高AC=AN+NC=600-250)米,故选B.
20.87
解析 如图,过点P作PC⊥AB,垂足为C,设PC=x米,在Rt△APC中,∠APC=30°,∴AC=PC·tan 30°=x(米).在Rt△BCP中,∠CPB=60°,∴BC=CP·tan 60°=x(米).∵AB=200米,∴AC+BC=200米,∴x=200,解得x=50≈87,∴点P到赛道AB的距离约为87米.
21.(38+15)
解析 如图,过点B作BF⊥DE于F,过点C作CG⊥BF于G,过点C作CH⊥DE于H,则四边形ABFE、四边形CGFH都是矩形,
∴AB=EF=24 cm,CG=HF,∠BGC=∠ABF=∠GCH=90°.
∵∠ABC=135°,∴∠CBG=∠ABC-∠ABF=45°,
∴∠BCG=90°-∠CBG=45°.
∵∠BCD=165°,∴∠DCH=∠BCD-∠BCG-∠GCH=30°.
在Rt△BCG中,BC=30 cm,∴CG=BC·sin 45°=30×
cm,在Rt△CDH中,CD=28 cm,
∴DH=CD·sin 30°=28×
)cm.
22.解析 (1)如图,过点B作BM⊥AF于点M,
由题可知,∠A=30°,∠DBE=53°,DF=600 m,AB=300 m,
在Rt△ABM中,∠A=30°,AB=300 m,
∴BM=AB=150 m,∴EF=BM=150 m,
∴DE=DF-EF=600-150=450(m).
答:登山缆车上升的高度DE为450 m.
(2)在Rt△BDE中,∠DBE=53°,DE=450 m,
∴BD==562.5(m),
∴需要的时间=步行时间+乘坐缆车时间=≈19.4(min).
答:从山底A处到达山顶D处大约需要19.4分钟.
23.解析 (1)如图,过C作OB的垂线分别交仰角线、俯角线于点E、D,交水平线于点F,
在Rt△AEF中,tan∠EAF=,
∴EF=AF·tan 15°≈130×0.27=35.1(cm),
∴CE=CF+EF=160+35.1=195.1(cm),
∴小杜最少需要下蹲208-195.1=12.9厘米才能被识别.
(2)小若能被识别.
理由:如图,过B作OB的垂线分别交仰角线、俯角线于M、N,交水平线于P,
在Rt△APM中,tan∠MAP=,
∴MP=AP·tan 20°≈150×0.36=54.0(cm),
∵∠MAP=∠NAP,AP=AP,∠APM=∠APN=90°,
∴△AMP≌△ANP(ASA),∴PN=MP=54.0 cm,
∴BN=160-54.0=106.0(cm),
∵120-15=105(cm),106.0 cm>105 cm,
∴小若必须踮起脚尖.
∵小若踮起脚尖后头顶距地面的高度为120+3=123(cm),
∴小若踮起脚尖后头顶超出点N的高度为123-106.0=17.0(cm)>15 cm,
∴小若能被识别.
素养探究全练
24.7.0米
解析 如图,延长BC、ED相交于点F,过点A作AG⊥EF,垂足为G,过点A作AH⊥CB,交CB的延长线于点H.
由题意,得AH=FG,AG=HF,BC=20米,EF⊥BF,
在Rt△ABH中,∠ABH=30°,AB=10米,
∴AH=AB=5(米),BH=(米),
∴GF=AH=5米.
∵斜坡CD的坡度i=3∶4,∴,∴设DF=3x米,则CF=4x米,
在Rt△CDF中,CD==5x(米),
∵CD=15米,∴5x=15,解得x=3,∴CF=12米,DF=9米,
∴AG=HF=BH+BC+CF=(32+5)米,在Rt△AGE中,∠EAG=15°,
∴EG=AG·tan 15°≈(32+5)×0.27≈10.98(米),
∴ED=EG+FG-DF=10.98+5-9≈7.0(米),∴大树ED的高度约为7.0米.
25.解析 如图,过点F作FQ⊥CD交直线CD于点Q,过点A作AP⊥MN于点P,过点C作CH⊥AB于点H.
∵四边形ABCD是平行四边形,∠FBA=114.2°,
∴∠FCQ=∠CBA=180°-114.2°=65.8°,
∴FQ=FC·sin∠FCQ=57sin 65.8° cm.
由题意知AB∥CD∥MN,FC∥AN,
则∠ANP=∠ADC=∠FCQ=65.8°,又AN=43 cm,
∴AP=AN·sin∠ANP=43sin 65.8° cm.
∵BC=CE,EB=16.4 cm,∴BH=8.2 cm,
∴CH=BH·tan∠CBH=8.2×tan 65.8°≈8.2×2.23≈18.29 cm,
∴靠背顶端F点距地面(MN)的高度为
FQ+AP-CH=57sin 65.8°+43sin 65.8°-18.29≈100×0.91-18.29=72.71
≈72.7 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
