第二十八章 锐角三角函数素养综合检测试题(含解析)
文档属性
| 名称 | 第二十八章 锐角三角函数素养综合检测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 556.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十八章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2023甘肃酒泉肃州三模)sin 60°的相反数是(M9228002)( )
A.-
2.(2023山东威海文登一模)利用科学计算器计算cos 35°,下列按键顺序正确的是( )
A.12cos35= B.21cos35=
C.1-2cos35= D.12cos35=
3.【新独家原创】在△ABC中,∠A,∠B均为锐角,且|2sin A-1|与互为相反数,则∠C的度数是(M9228002)( )
A.45° B.75° C.105° D.120°
4.(2023云南临沧耿马三模)在Rt△ABC中,∠C=90°,AB=2BC,则cos A的值为( )
A.
5.【新考向·新定义试题】(2023湖南娄底双峰一模)定义一种运算:cos(α+β)=cos αcos β-sin αsin β,cos(α-β)=cos αcos β+sin αsin β.例如:当α=60°,β=45°时,cos(60°-45°)=,则cos 75°的值为( )
A.
C.
6.(2022江苏镇江丹阳二模)已知一个不等臂跷跷板AB长4米,支撑柱OH垂直于地面,如图1,当AB的一端A着地时,AB与地面所夹锐角的正弦值为;如图2,当AB的另一端B着地时,AB与地面所夹锐角的正弦值为,则支撑柱OH的长为( )
A.0.5米 B.0.6米 C. 米 D.0.8米
7.【中华优秀传统文化】(2022江西景德镇模拟)刘徽是我国魏晋时期卓越的数学家,他在《九章算术注》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长.如图,正十二边形的边长是4,则可求出此十二边形的周长来近似代替其外接圆的周长,便可估计π的值,下面关于π的值表述正确的是( )
A.π≈ B.π≈
C.π≈6sin 15° D.π≈12sin 15°
8.(2022山东淄博张店一模)如图,在平面直角坐标系xOy中,AB=,延长AB至C,连接OC,若满足OC2=BC·AC,tan α=,则点C的坐标为( )
A.(-2,4) B.
C. D.(-1,2)
二、填空题(每小题4分,共24分)
9.【新独家原创】已知α为锐角,当无意义时,cos α的值是 .(M9228002)
10.【新独家原创】【设参法】如图,在△ABC中,∠C=90°,定义:斜边与∠A的对边的比叫做∠A的余割,用“csc A”表示.在△ABC中,
若tan A=,则csc A的值为 .
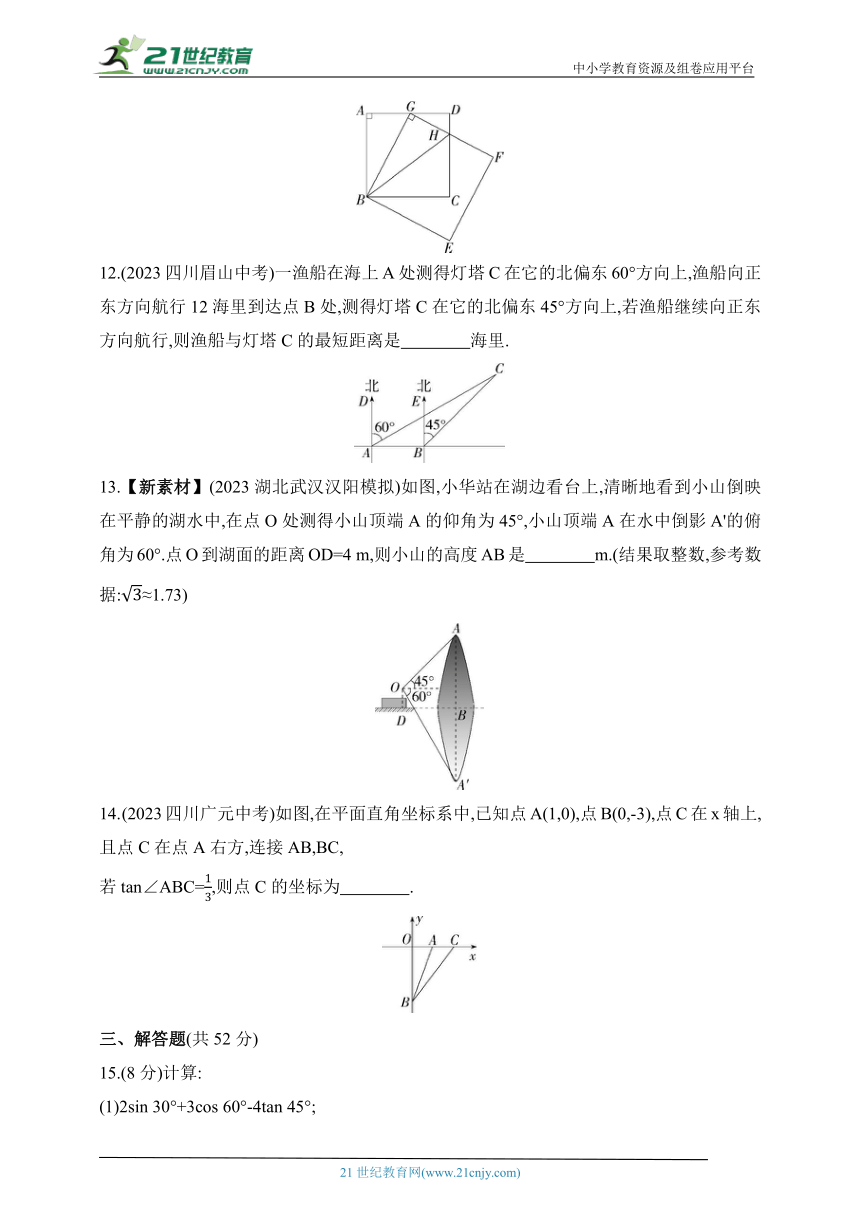
11.【三垂直模型】(2023四川巴中中考)如图,已知正方形ABCD和正方形BEFG,点G在AD上,GF与CD交于点H,tan∠ABG=,正方形ABCD的边长为8,则BH的长为 .
12.(2023四川眉山中考)一渔船在海上A处测得灯塔C在它的北偏东60°方向上,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向上,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 海里.
13.【新素材】(2023湖北武汉汉阳模拟)如图,小华站在湖边看台上,清晰地看到小山倒映在平静的湖水中,在点O处测得小山顶端A的仰角为45°,小山顶端A在水中倒影A'的俯角为60°.点O到湖面的距离OD=4 m,则小山的高度AB是 m.(结果取整数,参考数据:≈1.73)
(2023四川广元中考)如图,在平面直角坐标系中,已知点A(1,0),点B(0,-3),点C在x轴上,且点C在点A右方,连接AB,BC,
若tan∠ABC=,则点C的坐标为 .
三、解答题(共52分)
15.(8分)计算:
(1)2sin 30°+3cos 60°-4tan 45°;
(2)cos230°+sin245°-tan 60°·tan 30°.
16.(10分)(2023上海徐汇期末)如图,已知在△ABC中,CD⊥AB,垂足为点D,AD=2,BD=6,tan B=,点E是边BC的中点.
(1)求边AC的长;
(2)求∠EAB的正弦值.
17.(10分)(2023贵州中考)贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①所示的景区内修建观光索道.其设计示意图如图②所示,以山脚A为起点,沿途修建AB、CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC,BC长为50 m.索道AB与AF的夹角为15°,CD与水平线的夹角为45°,A、B两处的水平距离AE为576 m,DF⊥AF,垂足为点F.(图②中所有点都在同一平面内,点A、E、F在同一水平线上)
(1)求索道AB的长(结果精确到1 m);
(2)求AF的长(结果精确到1 m).
(参考数据:sin 15°≈0.25,cos 15°≈0.96,tan 15°≈0.26,≈1.41)
18.【方程思想】(12分)(2022辽宁营口中考)在一次数学课外实践活动中,某小组要测量一幢大楼MN的高度,如图,在山坡的坡脚A处测得大楼顶部M的仰角是58°,沿着山坡向上走75米到达B处,在B处测得大楼顶部M的仰角是22°,已知斜坡AB的坡度i=3∶4(坡度是指坡面的铅直高度与水平宽度的比),求大楼MN的高度.(图中的点A,B,M,N,C均在同一平面内,N,A,C在同一水平线上,参考数据:tan 22°≈0.4,tan 58°≈1.6)
19.【新考向·阅读理解试题】(12分)(2022湖南张家界中考)阅读下列材料:
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,求证:.
证明:如图,过点C作CD⊥AB于点D,
则在Rt△BCD中,CD=asin B,
在Rt△ACD中,CD=bsin A,
∴asin B=bsin A,
∴.
根据上面的材料解决下列问题:
(1)如图①,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,求证:;
(2)为了办好湖南省首届旅游发展大会,张家界市积极优化旅游环境.如图②,规划中的一片三角形区域需美化,已知∠A=67°,∠B=53°,AC=80 m,求这片区域的面积.(结果保留根号.参考数据:sin 53°≈0.8,sin 67°≈0.9)
答案全解全析
1.C ∵sin 60°=,∴sin 60°的相反数是-.故选C.
2.A 利用科学计算器计算cos 35°,按键顺序为12cos35=.故选A.
3.C 由题意,得2sin A-1=0,cos B-=0,即sin A=,cos B=,∴∠A=30°,∠B=45°,∴∠C=180°-∠A-∠B=105°.故选C.
4.A ∵AB=2BC,∴设BC=k,则AB=2k,∵∠C=90°,∴AC=k,∴cos A=,故选A.
5.B 由题意,得cos 75°=cos(30°+45°)=cos 30°cos 45°-sin 30°sin 45°=.故选B.
6.D 在Rt△AOH中,sin∠OAH=,∴OA=2OH,同理可得OB=3OH,∵AB=4,∴2OH+3OH=4,解得OH=0.8(米).故选D.
7.D 如图,由正十二边形的性质可知,∠AOB==30°,则∠AOM=∠AOB=15°,在Rt△AOM中,AM=OA·sin 15°,∴AB=2AM=2sin 15°·OA,∴正十二边形的周长为2sin 15°·OA×12,∴π≈=12sin 15°.故选D.
C 如图,过点C作CD⊥x轴,垂足为D,则∠OCD=∠BOC=α,
∵tan α=,∴CD=2DO.∵OC2=BC·AC,∴.
∵∠ACO=∠OCB,∴△CBO∽△COA,∴∠CAO=∠COB=α,∵tan α=,∴tan α=,∴AO=2BO.在Rt△ABO中,AO2+BO2=AB2,AB=,
∴4BO2+BO2=5,∴BO=1,∴AO=2BO=2.
∵CD∥BO,∴△BAO∽△CAD,∴,即,
解得OD=,∴点C的坐标为.故选C.
9.
解析 由题意,得tan α-1=0,∴tan α=,∴α=30°,∴cos α=cos 30°=.
10.
解析 ∵tan A=,∴设BC=k,则AC=2k,∴AB=k,∴csc A=.
11.10
解析 ∵四边形ABCD、BEFG均为正方形,∴∠A=∠BGF=∠D=90°,∴∠AGB+∠DGH=90°,∠AGB+∠ABG=90°,∴∠DGH=∠ABG,∴tan∠DGH=tan∠ABG=,∵正方形ABCD的边长为8,∴AB=AD=CD=8,在Rt△ABG中,AG=AB·tan∠ABG=8×=4,∴DG=AD-AG=4,在Rt△DGH中,DH=DG·tan∠DGH=4×=2,∴CH=CD-DH=8-2=6.在Rt△BCH中,BH==10.
12.6(+1)
解析 如图,过点C作CH⊥AB交直线AB于H.
∵∠DAC=60°,∠CBE=45°,
∴∠CAH=90°-∠DAC=30°,∠CBH=90°-∠CBE=45°,
∴∠BCH=90°-45°=45°=∠CBH,∴BH=CH.
在Rt△ACH中,∠CAH=30°,AH=AB+BH=12+CH,tan 30°=
(12+CH),解得CH=6(+1)海里,
即渔船与灯塔C的最短距离是6(+1)海里.
13.15
解析 如图,过点O作OE⊥AB,垂足为E,
由题意得AB=A'B,OE=DB,OD=EB=4 m,设OE=DB=x m,
在Rt△AOE中,∠AOE=45°,∴AE=OE·tan 45°=x(m),
∴AB=AE+BE=(x+4)m,
在Rt△OEA'中,∠EOA'=60°,∴A'E=OE·tan 60°=x-4,解得x=4+4+4≈15(m).
14.
解析 如图,作AD∥BC,交OB于点D.∵点A(1,0),点B(0,-3),∴OA=1,OB=3,∴tan∠OBA=,∵tan∠ABC=,∴∠OBA=∠ABC.∵AD∥BC,∴∠DAB=∠ABC,∴∠DBA=∠DAB,∴AD=BD.设OD=x,则AD=BD=3-x,在Rt△AOD中,12+x2=(3-x)2,解得x=.∵AD∥BC,∴,即.
15.解析 (1)原式=2×-4×1
=1+.
(2)原式=
=.
16.解析 (1)∵CD⊥AB,
∴△ACD、△BCD均为直角三角形.
在Rt△CDB中,∵BD=6,tan B=,
∴CD=4.
在Rt△CDA中,AC=.
(2)如图,过点E作EF⊥AB,垂足为F.
∵CD⊥AB,EF⊥AB,∴CD∥EF.
∴△BEF∽△BCD,又∵点E是边BC的中点,
∴DF=BF=3,EF=CD=2.
∴AF=AD+DF=5.
在Rt△AEF中,AE=.
∴sin∠EAB=.
17.解析 (1)在Rt△ABE中,∠AEB=90°,∠BAE=15°,AE=576 m,
∴AB=≈600(m),
即AB的长约为600 m.
(2)如图,延长BC交DF于G,
∵BC∥AE,∴∠CBE=90°.
∵DF⊥AF,∴∠AFD=90°,
又∵∠BEF=90°,
∴四边形BEFG为矩形,
∴EF=BG,∠CGD=∠BGF=90°.
∵CD=AB=600 m,∠DCG=45°,
∴CG=CD·cos∠DCG=600×cos 45°=600×(m),
∴AF=AE+EF=AE+BG=AE+BC+CG=576+50+300≈1 049(m),
即AF的长约为1 049 m.
18.解析 如图,过点B作BE⊥AC,垂足为E,过点B作BD⊥MN,垂足为D,则BE=DN,DB=NE.
∵斜坡AB的坡度i=3∶4,∴.
设BE=3a米,则AE=4a米.
在Rt△ABE中,AB==5a(米).
∵AB=75米,∴5a=75,∴a=15,
∴DN=BE=45米,AE=60米.
设NA=x米,则BD=NE=AN+AE=(x+60)米.
在Rt△ANM中,∠NAM=58°,
∴MN=AN·tan 58°≈1.6x(米),
∴DM=MN-DN=(1.6x-45)米,
在Rt△MDB中,∠MBD=22°,
∴tan 22°=≈0.4,∴x≈57.5,
∴MN=1.6x=92(米),
∴大楼MN的高度约为92米.
19.解析 (1)证明:如图①,过点A作AD⊥BC于点D,
在Rt△ABD中,AD=csin B,
在Rt△ACD中,AD=bsin C,
∴csin B=bsin C,∴.
(2)如图②,过点A作AE⊥BC于点E,
∵∠BAC=67°,∠B=53°,∴∠C=60°,
在Rt△ACE中,AE=AC·sin 60°=80×(m),
∵,
∴,∴BC≈90 m,
∴S△ABC==1 800(m2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十八章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2023甘肃酒泉肃州三模)sin 60°的相反数是(M9228002)( )
A.-
2.(2023山东威海文登一模)利用科学计算器计算cos 35°,下列按键顺序正确的是( )
A.12cos35= B.21cos35=
C.1-2cos35= D.12cos35=
3.【新独家原创】在△ABC中,∠A,∠B均为锐角,且|2sin A-1|与互为相反数,则∠C的度数是(M9228002)( )
A.45° B.75° C.105° D.120°
4.(2023云南临沧耿马三模)在Rt△ABC中,∠C=90°,AB=2BC,则cos A的值为( )
A.
5.【新考向·新定义试题】(2023湖南娄底双峰一模)定义一种运算:cos(α+β)=cos αcos β-sin αsin β,cos(α-β)=cos αcos β+sin αsin β.例如:当α=60°,β=45°时,cos(60°-45°)=,则cos 75°的值为( )
A.
C.
6.(2022江苏镇江丹阳二模)已知一个不等臂跷跷板AB长4米,支撑柱OH垂直于地面,如图1,当AB的一端A着地时,AB与地面所夹锐角的正弦值为;如图2,当AB的另一端B着地时,AB与地面所夹锐角的正弦值为,则支撑柱OH的长为( )
A.0.5米 B.0.6米 C. 米 D.0.8米
7.【中华优秀传统文化】(2022江西景德镇模拟)刘徽是我国魏晋时期卓越的数学家,他在《九章算术注》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的周长.如图,正十二边形的边长是4,则可求出此十二边形的周长来近似代替其外接圆的周长,便可估计π的值,下面关于π的值表述正确的是( )
A.π≈ B.π≈
C.π≈6sin 15° D.π≈12sin 15°
8.(2022山东淄博张店一模)如图,在平面直角坐标系xOy中,AB=,延长AB至C,连接OC,若满足OC2=BC·AC,tan α=,则点C的坐标为( )
A.(-2,4) B.
C. D.(-1,2)
二、填空题(每小题4分,共24分)
9.【新独家原创】已知α为锐角,当无意义时,cos α的值是 .(M9228002)
10.【新独家原创】【设参法】如图,在△ABC中,∠C=90°,定义:斜边与∠A的对边的比叫做∠A的余割,用“csc A”表示.在△ABC中,
若tan A=,则csc A的值为 .
11.【三垂直模型】(2023四川巴中中考)如图,已知正方形ABCD和正方形BEFG,点G在AD上,GF与CD交于点H,tan∠ABG=,正方形ABCD的边长为8,则BH的长为 .
12.(2023四川眉山中考)一渔船在海上A处测得灯塔C在它的北偏东60°方向上,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向上,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是 海里.
13.【新素材】(2023湖北武汉汉阳模拟)如图,小华站在湖边看台上,清晰地看到小山倒映在平静的湖水中,在点O处测得小山顶端A的仰角为45°,小山顶端A在水中倒影A'的俯角为60°.点O到湖面的距离OD=4 m,则小山的高度AB是 m.(结果取整数,参考数据:≈1.73)
(2023四川广元中考)如图,在平面直角坐标系中,已知点A(1,0),点B(0,-3),点C在x轴上,且点C在点A右方,连接AB,BC,
若tan∠ABC=,则点C的坐标为 .
三、解答题(共52分)
15.(8分)计算:
(1)2sin 30°+3cos 60°-4tan 45°;
(2)cos230°+sin245°-tan 60°·tan 30°.
16.(10分)(2023上海徐汇期末)如图,已知在△ABC中,CD⊥AB,垂足为点D,AD=2,BD=6,tan B=,点E是边BC的中点.
(1)求边AC的长;
(2)求∠EAB的正弦值.
17.(10分)(2023贵州中考)贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①所示的景区内修建观光索道.其设计示意图如图②所示,以山脚A为起点,沿途修建AB、CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC,BC长为50 m.索道AB与AF的夹角为15°,CD与水平线的夹角为45°,A、B两处的水平距离AE为576 m,DF⊥AF,垂足为点F.(图②中所有点都在同一平面内,点A、E、F在同一水平线上)
(1)求索道AB的长(结果精确到1 m);
(2)求AF的长(结果精确到1 m).
(参考数据:sin 15°≈0.25,cos 15°≈0.96,tan 15°≈0.26,≈1.41)
18.【方程思想】(12分)(2022辽宁营口中考)在一次数学课外实践活动中,某小组要测量一幢大楼MN的高度,如图,在山坡的坡脚A处测得大楼顶部M的仰角是58°,沿着山坡向上走75米到达B处,在B处测得大楼顶部M的仰角是22°,已知斜坡AB的坡度i=3∶4(坡度是指坡面的铅直高度与水平宽度的比),求大楼MN的高度.(图中的点A,B,M,N,C均在同一平面内,N,A,C在同一水平线上,参考数据:tan 22°≈0.4,tan 58°≈1.6)
19.【新考向·阅读理解试题】(12分)(2022湖南张家界中考)阅读下列材料:
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,求证:.
证明:如图,过点C作CD⊥AB于点D,
则在Rt△BCD中,CD=asin B,
在Rt△ACD中,CD=bsin A,
∴asin B=bsin A,
∴.
根据上面的材料解决下列问题:
(1)如图①,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,求证:;
(2)为了办好湖南省首届旅游发展大会,张家界市积极优化旅游环境.如图②,规划中的一片三角形区域需美化,已知∠A=67°,∠B=53°,AC=80 m,求这片区域的面积.(结果保留根号.参考数据:sin 53°≈0.8,sin 67°≈0.9)
答案全解全析
1.C ∵sin 60°=,∴sin 60°的相反数是-.故选C.
2.A 利用科学计算器计算cos 35°,按键顺序为12cos35=.故选A.
3.C 由题意,得2sin A-1=0,cos B-=0,即sin A=,cos B=,∴∠A=30°,∠B=45°,∴∠C=180°-∠A-∠B=105°.故选C.
4.A ∵AB=2BC,∴设BC=k,则AB=2k,∵∠C=90°,∴AC=k,∴cos A=,故选A.
5.B 由题意,得cos 75°=cos(30°+45°)=cos 30°cos 45°-sin 30°sin 45°=.故选B.
6.D 在Rt△AOH中,sin∠OAH=,∴OA=2OH,同理可得OB=3OH,∵AB=4,∴2OH+3OH=4,解得OH=0.8(米).故选D.
7.D 如图,由正十二边形的性质可知,∠AOB==30°,则∠AOM=∠AOB=15°,在Rt△AOM中,AM=OA·sin 15°,∴AB=2AM=2sin 15°·OA,∴正十二边形的周长为2sin 15°·OA×12,∴π≈=12sin 15°.故选D.
C 如图,过点C作CD⊥x轴,垂足为D,则∠OCD=∠BOC=α,
∵tan α=,∴CD=2DO.∵OC2=BC·AC,∴.
∵∠ACO=∠OCB,∴△CBO∽△COA,∴∠CAO=∠COB=α,∵tan α=,∴tan α=,∴AO=2BO.在Rt△ABO中,AO2+BO2=AB2,AB=,
∴4BO2+BO2=5,∴BO=1,∴AO=2BO=2.
∵CD∥BO,∴△BAO∽△CAD,∴,即,
解得OD=,∴点C的坐标为.故选C.
9.
解析 由题意,得tan α-1=0,∴tan α=,∴α=30°,∴cos α=cos 30°=.
10.
解析 ∵tan A=,∴设BC=k,则AC=2k,∴AB=k,∴csc A=.
11.10
解析 ∵四边形ABCD、BEFG均为正方形,∴∠A=∠BGF=∠D=90°,∴∠AGB+∠DGH=90°,∠AGB+∠ABG=90°,∴∠DGH=∠ABG,∴tan∠DGH=tan∠ABG=,∵正方形ABCD的边长为8,∴AB=AD=CD=8,在Rt△ABG中,AG=AB·tan∠ABG=8×=4,∴DG=AD-AG=4,在Rt△DGH中,DH=DG·tan∠DGH=4×=2,∴CH=CD-DH=8-2=6.在Rt△BCH中,BH==10.
12.6(+1)
解析 如图,过点C作CH⊥AB交直线AB于H.
∵∠DAC=60°,∠CBE=45°,
∴∠CAH=90°-∠DAC=30°,∠CBH=90°-∠CBE=45°,
∴∠BCH=90°-45°=45°=∠CBH,∴BH=CH.
在Rt△ACH中,∠CAH=30°,AH=AB+BH=12+CH,tan 30°=
(12+CH),解得CH=6(+1)海里,
即渔船与灯塔C的最短距离是6(+1)海里.
13.15
解析 如图,过点O作OE⊥AB,垂足为E,
由题意得AB=A'B,OE=DB,OD=EB=4 m,设OE=DB=x m,
在Rt△AOE中,∠AOE=45°,∴AE=OE·tan 45°=x(m),
∴AB=AE+BE=(x+4)m,
在Rt△OEA'中,∠EOA'=60°,∴A'E=OE·tan 60°=x-4,解得x=4+4+4≈15(m).
14.
解析 如图,作AD∥BC,交OB于点D.∵点A(1,0),点B(0,-3),∴OA=1,OB=3,∴tan∠OBA=,∵tan∠ABC=,∴∠OBA=∠ABC.∵AD∥BC,∴∠DAB=∠ABC,∴∠DBA=∠DAB,∴AD=BD.设OD=x,则AD=BD=3-x,在Rt△AOD中,12+x2=(3-x)2,解得x=.∵AD∥BC,∴,即.
15.解析 (1)原式=2×-4×1
=1+.
(2)原式=
=.
16.解析 (1)∵CD⊥AB,
∴△ACD、△BCD均为直角三角形.
在Rt△CDB中,∵BD=6,tan B=,
∴CD=4.
在Rt△CDA中,AC=.
(2)如图,过点E作EF⊥AB,垂足为F.
∵CD⊥AB,EF⊥AB,∴CD∥EF.
∴△BEF∽△BCD,又∵点E是边BC的中点,
∴DF=BF=3,EF=CD=2.
∴AF=AD+DF=5.
在Rt△AEF中,AE=.
∴sin∠EAB=.
17.解析 (1)在Rt△ABE中,∠AEB=90°,∠BAE=15°,AE=576 m,
∴AB=≈600(m),
即AB的长约为600 m.
(2)如图,延长BC交DF于G,
∵BC∥AE,∴∠CBE=90°.
∵DF⊥AF,∴∠AFD=90°,
又∵∠BEF=90°,
∴四边形BEFG为矩形,
∴EF=BG,∠CGD=∠BGF=90°.
∵CD=AB=600 m,∠DCG=45°,
∴CG=CD·cos∠DCG=600×cos 45°=600×(m),
∴AF=AE+EF=AE+BG=AE+BC+CG=576+50+300≈1 049(m),
即AF的长约为1 049 m.
18.解析 如图,过点B作BE⊥AC,垂足为E,过点B作BD⊥MN,垂足为D,则BE=DN,DB=NE.
∵斜坡AB的坡度i=3∶4,∴.
设BE=3a米,则AE=4a米.
在Rt△ABE中,AB==5a(米).
∵AB=75米,∴5a=75,∴a=15,
∴DN=BE=45米,AE=60米.
设NA=x米,则BD=NE=AN+AE=(x+60)米.
在Rt△ANM中,∠NAM=58°,
∴MN=AN·tan 58°≈1.6x(米),
∴DM=MN-DN=(1.6x-45)米,
在Rt△MDB中,∠MBD=22°,
∴tan 22°=≈0.4,∴x≈57.5,
∴MN=1.6x=92(米),
∴大楼MN的高度约为92米.
19.解析 (1)证明:如图①,过点A作AD⊥BC于点D,
在Rt△ABD中,AD=csin B,
在Rt△ACD中,AD=bsin C,
∴csin B=bsin C,∴.
(2)如图②,过点A作AE⊥BC于点E,
∵∠BAC=67°,∠B=53°,∴∠C=60°,
在Rt△ACE中,AE=AC·sin 60°=80×(m),
∵,
∴,∴BC≈90 m,
∴S△ABC==1 800(m2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
