第二十六章 反比例函数素养综合检测试题(含解析)
文档属性
| 名称 | 第二十六章 反比例函数素养综合检测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 498.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:15:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
第二十六章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2023重庆九龙坡期末)下列函数中,y是x的反比例函数的是( )
A.y=
C.y=-2x D.y=x-1
2.【新独家原创】两个变量x和y具有下列关系,其中y与x成反比例函数关系的是( )
A.互为相反数 B.互为倒数
C.相等 D.绝对值相等
3.(2023湖南株洲中考)下列哪个点在反比例函数y=的图象上 ( )
A.P1(1,-4) B.P2(4,-1)
C.P3(2,4) D.P4(2)
4.(2023四川绵阳期末)一次函数y=mx和反比例函数y=的图象的一个交点坐标为(-3,4),则另一个交点坐标为( )
A.(3,-4) B.(-3,-4)
C.(3,4) D.(4,-3)
5.(2023山东青岛崂山一模)如图,直线y=k1x+b与双曲线y=交于A、B两点,其横坐标分别为1和5,则不等式k1x+b<的解集是( )
A.15或x<1
C.x>5或06.(2023黑龙江鸡西二模)如图,点B在y轴的正半轴上,点C在反比例函数y=-(x<0)的图象上,则菱形OABC的面积为( )
A.16 B.8 C.4 D.2
7.【跨学科·物理】(2021甘肃酒泉瓜州期末)在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体对气缸壁产生的压强p(kPa)与气体的体积V(mL)的关系可以用如图所示的反比例函数图象进行表示,下列说法错误的是( )
A.若气压p与体积V的表达式为p=,则k>0
B.当p=70时,70C.当体积V变为原来的时,对应的气压p变为原来的倍
D.当60≤V≤100时,气压p随着体积V的增大而减小
8.(2022山东滨州中考)在同一平面直角坐标系中,函数y=kx+1与y=
-(k为常数且k≠0)的大致图象可能是( )
二、填空题(每小题4分,共24分)
9.【新独家原创】若函数y=m是反比例函数,则2 024m的值为 .
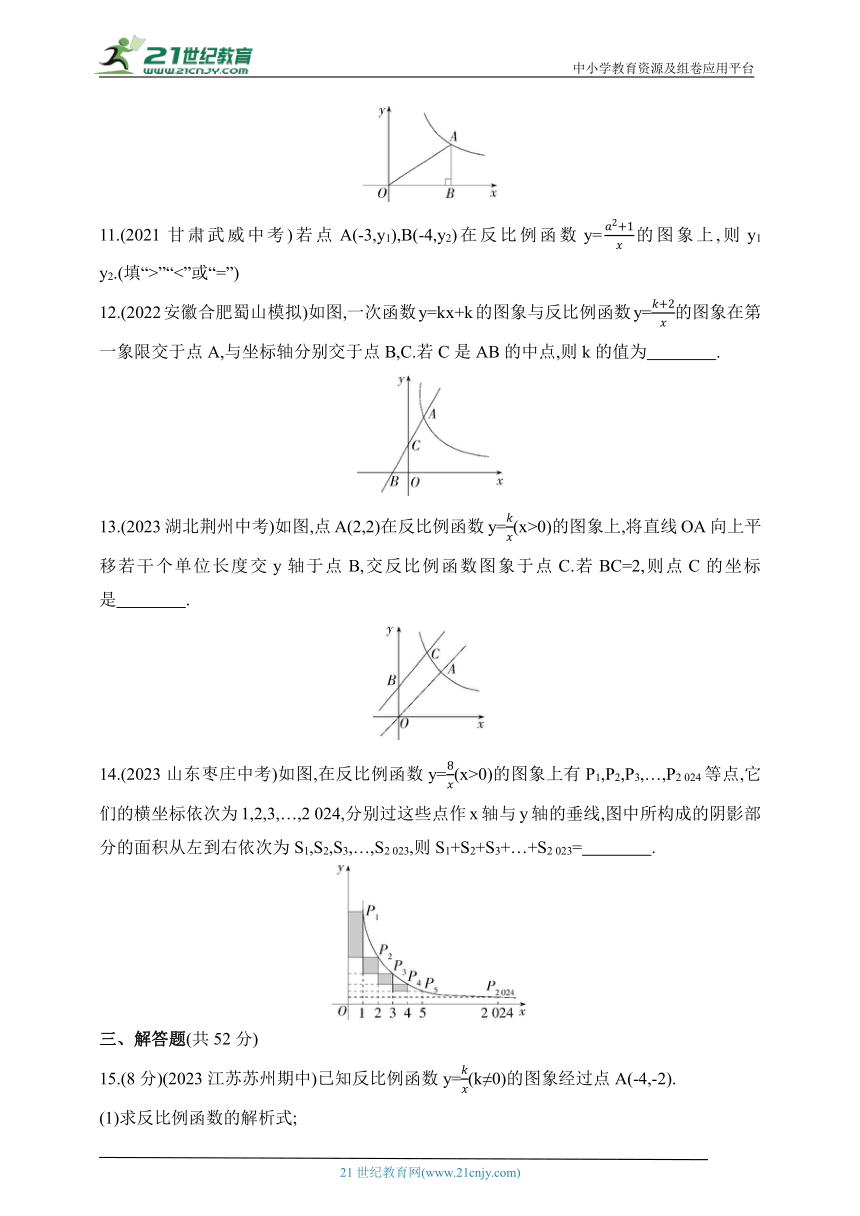
10.(2022四川凉山州中考)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴于点B,若△OAB的面积为3,则k= .
11.(2021甘肃武威中考)若点A(-3,y1),B(-4,y2)在反比例函数y=的图象上,则y1 y2.(填“>”“<”或“=”)
12.(2022安徽合肥蜀山模拟)如图,一次函数y=kx+k的图象与反比例函数y=的图象在第一象限交于点A,与坐标轴分别交于点B,C.若C是AB的中点,则k的值为 .
13.(2023湖北荆州中考)如图,点A(2,2)在反比例函数y=(x>0)的图象上,将直线OA向上平移若干个单位长度交y轴于点B,交反比例函数图象于点C.若BC=2,则点C的坐标是 .
14.(2023山东枣庄中考)如图,在反比例函数y=(x>0)的图象上有P1,P2,P3,…,P2 024等点,它们的横坐标依次为1,2,3,…,2 024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,S2 023,则S1+S2+S3+…+S2 023= .
三、解答题(共52分)
15.(8分)(2023江苏苏州期中)已知反比例函数y=(k≠0)的图象经过点A(-4,-2).
(1)求反比例函数的解析式;
(2)若点B在该函数图象上,求m的值.
16.(10分)(2022浙江杭州上城模拟)某市政府计划建设一项水利工程,工程需要运送的土石方总量为106立方米,某运输公司承担了运送土石方的任务.
(1)设该公司平均每天运送土石方总量为y立方米,完成运送任务所需时间为t天.
①求y关于t的函数表达式;
②当0(2)若1辆卡车每天可运送土石方102立方米,工期要求在80天内完成,则公司至少要安排多少辆相同型号的卡车运送
17.(10分)(2023湖南常德中考)如图所示,一次函数y1=-x+m与反比例函数y2=的图象相交于点A和点B(3,-1).
(1)求m的值和反比例函数的解析式;
(2)当y1>y2时,求x的取值范围.
18.【跨学科·物理】(12分)(2021江西景德镇乐平期末)电灭蚊器的电阻y(kΩ)随温度x(℃)变化的大致图象如图所示,通电后温度由10 ℃上升到30 ℃时,电阻与温度成反比例函数关系,且在温度达到30 ℃时,电阻下降到最小值,随后电阻随温度的升高而增加,温度每上升1 ℃,电阻增加 kΩ.
(1)当10≤x≤30时,求y与x的函数关系式;
(2)当x=30时,求y的值,并求当x>30时,y与x的函数关系式;
(3)电灭蚊器在使用过程中,温度x在什么范围内时,电阻不超过5 kΩ
19.(12分)(2022四川达州中考)如图,一次函数y=x+1与反比例函数y=的图象相交于A(m,2),B两点,分别连接OA,OB.
(1)求这个反比例函数的表达式;
(2)求△AOB的面积;
(3)在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
答案全解全析
1.D 选项A,y=,y是x的正比例函数;选项B,y=,y不是x的反比例函数;选项C,y=-2x,y是x的正比例函数;选项D,y=x-1,y是x的反比例函数.故选D.
2.B 选项A,∵x,y互为相反数,∴y=-x,则y是x的正比例函数;选项B,∵x,y互为倒数,∴xy=1,即y=,则y是x的反比例函数;选项C,∵x,y相等,∴y=x,则y是x的正比例函数;选项D,∵x,y的绝对值相等,∴|y|=|x|,显然,y与x不成反比例函数关系.故选B.
3.D ∵1×(-4)=4×(-1)=-4≠4,∴P1(1,-4)和P2(4,-1)不在反比例函数y=的图象上;∵2×4=8≠4,∴P3(2,4)不在反比例函数y=的图象上;∵2)在反比例函数y=的图象上.故选D.
4.A 一次函数y=mx与反比例函数y=的图象都关于原点成中心对称,∵一次函数y=mx和反比例函数y=的图象的一个交点坐标为(-3,4),∴另一个交点坐标为(3,-4).故选A.
5.C 由题图可知,当x>5或05或06.B 如图,连接AC交OB于D,∵四边形OABC是菱形,∴AC⊥OB.又∵点C在反比例函数y=-(x<0)的图象上,∴S△COD=×|-4|=2,∴S菱形OABC=4×S△COD=8.故选B.
7.B 观察题图,当V=60时,p=100,则pV=6 000,∴p与V的函数表达式为p=.
A项,若气压p与体积V的表达式为p=,则k=6 000>0,A正确,不符合题意;
B项,当p=70时,V=>80,B错误,符合题意;
C项,当体积V变为原来的时,对应的气压p变为原来的倍,C正确,不符合题意;
D项,当60≤V≤100时,气压p随着体积V的增大而减小,D正确,不符合题意.
故选B.
8.A 当k>0时,-k<0,一次函数y=kx+1的图象经过第一、二、三象限,且经过点(0,1),反比例函数y=-的图象位于第二、四象限,故A选项符合;当k<0时,一次函数y=kx+1的图象经过第一、二、四象限,无选项符合.故选A.
9.
解析 由题意,得m2+m-1=-1且m≠0,∴m=-1,∴2 024m=2 024-1=.
10.6
解析 ∵△OAB的面积为3,点A在反比例函数y=(x>0)的图象上,∴=3,∴|k|=6.∵k>0,∴k=6.
11.<
解析 ∵k=a2+1>0,∴反比例函数y=的图象位于第一、三象限,且在每个象限内,y随x的增大而减小,∵点A(-3,y1),B(-4,y2)同在第三象限,且-3>-4,∴y112.2
解析 ∵一次函数y=kx+k的图象与坐标轴分别交于点B,C,∴令y=0,得kx+k=0,解得x=-1,∴点B的坐标为(-1,0);令x=0,得y=k,∴点C的坐标为(0,k),又∵C是AB的中点,∴点A的坐标为(1,2k),∵点A在反比例函数y=的图象上,∴1×2k=k+2,∴k=2.
13.()
解析 ∵点A(2,2)在反比例函数y=(x>0)的图象上,∴2=,∴k=4,∴反比例函数解析式为y=(x>0).如图,作AD⊥x轴,CH⊥x轴,BG⊥CH,垂足分别为D,H,G.∵A(2,2),∴AD=OD,∴∠AOD=45°,∴∠AOB=45°.∵OA∥BC,∴∠CBO=180°-45°=135°,又易知∠OBG=90°,∴∠CBG=135°-90°=45°,∴∠CBG=∠BCG=45°.∵BC=2,∴BG=CG=,∴C点的横坐标为.又C在反比例函数y=的图象上,∴C().
14.
解析 ∵P1,P2,P3,…,P2 024的横坐标依次为1,2,3,…,2 024,∴阴影矩形的一边长都为1,如图,将除第一个阴影矩形外的所有阴影矩形向左平移至y轴,可得S1+S2+S3+…+S2 023=,把x=2 024代入y=,得y=,即OA=,∴S矩形OABC=OA·OC=,由k的几何意义得,
即S1+S2+S3+…+S2 023=.
15.解析 (1)∵反比例函数y=(k≠0)的图象经过点A(-4,-2),
∴k=-4×(-2)=8,
∴反比例函数的解析式为y=.
(2)∵点B在该函数图象上,
∴,解得m=±4,
∴m的值为±4.
16.解析 (1)①由题意得y=,
∴y关于t的函数表达式为y=.
②当0∴当t=80时,y有最小值,为=12 500,
当t逐渐接近0时,y值趋于无穷大,
∴y的取值范围为y≥12 500.
(2)设安排x辆相同型号的卡车运送,
依题意得102x×80≥106,解得x≥125,
∴公司至少要安排125辆相同型号的卡车运送.
17.解析 (1)∵一次函数y1=-x+m与反比例函数y2=的图象相交于点A和点B(3,-1),
∴-1=-3+m,-1=,
解得m=2,k=-3,
∴m的值为2,反比例函数的解析式为y2=-.
(2)解方程组
∴A(-1,3),
观察题图可得,当y1>y2时,x的取值范围为x<-1或018.解析 (1)当10≤x≤30时,设y=(m≠0),
∵图象过点(10,6),∴m=xy=10×6=60.
∴当10≤x≤30时,y与x的函数关系式为y=.
(2)∵当10≤x≤30时,y=,
∴当x=30时,y==2.
当x≥30时,设y=kx+b,
∵图象过点(30,2),且温度每上升1 ℃,电阻增加 kΩ,
∴
故当x>30时,y与x的函数关系式为y=x-6.
(3)对于y=,当y=5时,x=12;
对于y=x-6,当y=5时,x=41,
结合图象可知温度x在12 ℃≤x≤℃的范围内时,电阻不超过5 kΩ.
19.解析 (1)∵一次函数y=x+1的图象经过点A(m,2),
∴m+1=2,∴m=1,∴A(1,2).
∵反比例函数y=的图象经过点A(1,2),∴k=2,
∴反比例函数的表达式为y=.
(2)解方程组
∴B(-2,-1).
∵对于一次函数y=x+1,当x=0时,y=1,
∴C(0,1),
∴S△AOB=S△AOC+S△BOC=×1×2=1.5.
(3)存在.满足条件的点P的坐标为(-3,-3)或(-1,1)或(3,3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
第二十六章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共24分)
1.(2023重庆九龙坡期末)下列函数中,y是x的反比例函数的是( )
A.y=
C.y=-2x D.y=x-1
2.【新独家原创】两个变量x和y具有下列关系,其中y与x成反比例函数关系的是( )
A.互为相反数 B.互为倒数
C.相等 D.绝对值相等
3.(2023湖南株洲中考)下列哪个点在反比例函数y=的图象上 ( )
A.P1(1,-4) B.P2(4,-1)
C.P3(2,4) D.P4(2)
4.(2023四川绵阳期末)一次函数y=mx和反比例函数y=的图象的一个交点坐标为(-3,4),则另一个交点坐标为( )
A.(3,-4) B.(-3,-4)
C.(3,4) D.(4,-3)
5.(2023山东青岛崂山一模)如图,直线y=k1x+b与双曲线y=交于A、B两点,其横坐标分别为1和5,则不等式k1x+b<的解集是( )
A.1
C.x>5或0
A.16 B.8 C.4 D.2
7.【跨学科·物理】(2021甘肃酒泉瓜州期末)在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气缸内气体对气缸壁产生的压强p(kPa)与气体的体积V(mL)的关系可以用如图所示的反比例函数图象进行表示,下列说法错误的是( )
A.若气压p与体积V的表达式为p=,则k>0
B.当p=70时,70
D.当60≤V≤100时,气压p随着体积V的增大而减小
8.(2022山东滨州中考)在同一平面直角坐标系中,函数y=kx+1与y=
-(k为常数且k≠0)的大致图象可能是( )
二、填空题(每小题4分,共24分)
9.【新独家原创】若函数y=m是反比例函数,则2 024m的值为 .
10.(2022四川凉山州中考)如图,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴于点B,若△OAB的面积为3,则k= .
11.(2021甘肃武威中考)若点A(-3,y1),B(-4,y2)在反比例函数y=的图象上,则y1 y2.(填“>”“<”或“=”)
12.(2022安徽合肥蜀山模拟)如图,一次函数y=kx+k的图象与反比例函数y=的图象在第一象限交于点A,与坐标轴分别交于点B,C.若C是AB的中点,则k的值为 .
13.(2023湖北荆州中考)如图,点A(2,2)在反比例函数y=(x>0)的图象上,将直线OA向上平移若干个单位长度交y轴于点B,交反比例函数图象于点C.若BC=2,则点C的坐标是 .
14.(2023山东枣庄中考)如图,在反比例函数y=(x>0)的图象上有P1,P2,P3,…,P2 024等点,它们的横坐标依次为1,2,3,…,2 024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,S2 023,则S1+S2+S3+…+S2 023= .
三、解答题(共52分)
15.(8分)(2023江苏苏州期中)已知反比例函数y=(k≠0)的图象经过点A(-4,-2).
(1)求反比例函数的解析式;
(2)若点B在该函数图象上,求m的值.
16.(10分)(2022浙江杭州上城模拟)某市政府计划建设一项水利工程,工程需要运送的土石方总量为106立方米,某运输公司承担了运送土石方的任务.
(1)设该公司平均每天运送土石方总量为y立方米,完成运送任务所需时间为t天.
①求y关于t的函数表达式;
②当0
17.(10分)(2023湖南常德中考)如图所示,一次函数y1=-x+m与反比例函数y2=的图象相交于点A和点B(3,-1).
(1)求m的值和反比例函数的解析式;
(2)当y1>y2时,求x的取值范围.
18.【跨学科·物理】(12分)(2021江西景德镇乐平期末)电灭蚊器的电阻y(kΩ)随温度x(℃)变化的大致图象如图所示,通电后温度由10 ℃上升到30 ℃时,电阻与温度成反比例函数关系,且在温度达到30 ℃时,电阻下降到最小值,随后电阻随温度的升高而增加,温度每上升1 ℃,电阻增加 kΩ.
(1)当10≤x≤30时,求y与x的函数关系式;
(2)当x=30时,求y的值,并求当x>30时,y与x的函数关系式;
(3)电灭蚊器在使用过程中,温度x在什么范围内时,电阻不超过5 kΩ
19.(12分)(2022四川达州中考)如图,一次函数y=x+1与反比例函数y=的图象相交于A(m,2),B两点,分别连接OA,OB.
(1)求这个反比例函数的表达式;
(2)求△AOB的面积;
(3)在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形 若存在,请直接写出点P的坐标;若不存在,请说明理由.
答案全解全析
1.D 选项A,y=,y是x的正比例函数;选项B,y=,y不是x的反比例函数;选项C,y=-2x,y是x的正比例函数;选项D,y=x-1,y是x的反比例函数.故选D.
2.B 选项A,∵x,y互为相反数,∴y=-x,则y是x的正比例函数;选项B,∵x,y互为倒数,∴xy=1,即y=,则y是x的反比例函数;选项C,∵x,y相等,∴y=x,则y是x的正比例函数;选项D,∵x,y的绝对值相等,∴|y|=|x|,显然,y与x不成反比例函数关系.故选B.
3.D ∵1×(-4)=4×(-1)=-4≠4,∴P1(1,-4)和P2(4,-1)不在反比例函数y=的图象上;∵2×4=8≠4,∴P3(2,4)不在反比例函数y=的图象上;∵2)在反比例函数y=的图象上.故选D.
4.A 一次函数y=mx与反比例函数y=的图象都关于原点成中心对称,∵一次函数y=mx和反比例函数y=的图象的一个交点坐标为(-3,4),∴另一个交点坐标为(3,-4).故选A.
5.C 由题图可知,当x>5或0
7.B 观察题图,当V=60时,p=100,则pV=6 000,∴p与V的函数表达式为p=.
A项,若气压p与体积V的表达式为p=,则k=6 000>0,A正确,不符合题意;
B项,当p=70时,V=>80,B错误,符合题意;
C项,当体积V变为原来的时,对应的气压p变为原来的倍,C正确,不符合题意;
D项,当60≤V≤100时,气压p随着体积V的增大而减小,D正确,不符合题意.
故选B.
8.A 当k>0时,-k<0,一次函数y=kx+1的图象经过第一、二、三象限,且经过点(0,1),反比例函数y=-的图象位于第二、四象限,故A选项符合;当k<0时,一次函数y=kx+1的图象经过第一、二、四象限,无选项符合.故选A.
9.
解析 由题意,得m2+m-1=-1且m≠0,∴m=-1,∴2 024m=2 024-1=.
10.6
解析 ∵△OAB的面积为3,点A在反比例函数y=(x>0)的图象上,∴=3,∴|k|=6.∵k>0,∴k=6.
11.<
解析 ∵k=a2+1>0,∴反比例函数y=的图象位于第一、三象限,且在每个象限内,y随x的增大而减小,∵点A(-3,y1),B(-4,y2)同在第三象限,且-3>-4,∴y1
解析 ∵一次函数y=kx+k的图象与坐标轴分别交于点B,C,∴令y=0,得kx+k=0,解得x=-1,∴点B的坐标为(-1,0);令x=0,得y=k,∴点C的坐标为(0,k),又∵C是AB的中点,∴点A的坐标为(1,2k),∵点A在反比例函数y=的图象上,∴1×2k=k+2,∴k=2.
13.()
解析 ∵点A(2,2)在反比例函数y=(x>0)的图象上,∴2=,∴k=4,∴反比例函数解析式为y=(x>0).如图,作AD⊥x轴,CH⊥x轴,BG⊥CH,垂足分别为D,H,G.∵A(2,2),∴AD=OD,∴∠AOD=45°,∴∠AOB=45°.∵OA∥BC,∴∠CBO=180°-45°=135°,又易知∠OBG=90°,∴∠CBG=135°-90°=45°,∴∠CBG=∠BCG=45°.∵BC=2,∴BG=CG=,∴C点的横坐标为.又C在反比例函数y=的图象上,∴C().
14.
解析 ∵P1,P2,P3,…,P2 024的横坐标依次为1,2,3,…,2 024,∴阴影矩形的一边长都为1,如图,将除第一个阴影矩形外的所有阴影矩形向左平移至y轴,可得S1+S2+S3+…+S2 023=,把x=2 024代入y=,得y=,即OA=,∴S矩形OABC=OA·OC=,由k的几何意义得,
即S1+S2+S3+…+S2 023=.
15.解析 (1)∵反比例函数y=(k≠0)的图象经过点A(-4,-2),
∴k=-4×(-2)=8,
∴反比例函数的解析式为y=.
(2)∵点B在该函数图象上,
∴,解得m=±4,
∴m的值为±4.
16.解析 (1)①由题意得y=,
∴y关于t的函数表达式为y=.
②当0
当t逐渐接近0时,y值趋于无穷大,
∴y的取值范围为y≥12 500.
(2)设安排x辆相同型号的卡车运送,
依题意得102x×80≥106,解得x≥125,
∴公司至少要安排125辆相同型号的卡车运送.
17.解析 (1)∵一次函数y1=-x+m与反比例函数y2=的图象相交于点A和点B(3,-1),
∴-1=-3+m,-1=,
解得m=2,k=-3,
∴m的值为2,反比例函数的解析式为y2=-.
(2)解方程组
∴A(-1,3),
观察题图可得,当y1>y2时,x的取值范围为x<-1或0
∵图象过点(10,6),∴m=xy=10×6=60.
∴当10≤x≤30时,y与x的函数关系式为y=.
(2)∵当10≤x≤30时,y=,
∴当x=30时,y==2.
当x≥30时,设y=kx+b,
∵图象过点(30,2),且温度每上升1 ℃,电阻增加 kΩ,
∴
故当x>30时,y与x的函数关系式为y=x-6.
(3)对于y=,当y=5时,x=12;
对于y=x-6,当y=5时,x=41,
结合图象可知温度x在12 ℃≤x≤℃的范围内时,电阻不超过5 kΩ.
19.解析 (1)∵一次函数y=x+1的图象经过点A(m,2),
∴m+1=2,∴m=1,∴A(1,2).
∵反比例函数y=的图象经过点A(1,2),∴k=2,
∴反比例函数的表达式为y=.
(2)解方程组
∴B(-2,-1).
∵对于一次函数y=x+1,当x=0时,y=1,
∴C(0,1),
∴S△AOB=S△AOC+S△BOC=×1×2=1.5.
(3)存在.满足条件的点P的坐标为(-3,-3)或(-1,1)或(3,3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
