2024人教版数学九年级下学期课时练--期中素养综合测试(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--期中素养综合测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 713.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:22:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
期中素养综合测试
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.【新独家原创】以下命题为假命题的是( )
A.任意两个等边三角形都相似
B.两边成比例且一角相等的两个三角形相似
C.相似多边形周长的比等于相似比
D.相似三角形面积的比等于相似比的平方
2.(2023河北保定莲池三模)如图,函数y=在第一象限的图象将所标的三个整点分隔开,则整数k的值可能是( )
A.10
B.8
C.7
D.6
3.(2023湖北武汉新洲模拟)已知反比例函数表达式为y=-,则下列说法正确的是( )
A.函数图象位于第一、三象限
B.点(2,3)在该函数图象上
C.当x<0时,y随x的增大而增大
D.当y≥-2时,x≥3
4.(2023浙江嘉兴中考)如图,在直角坐标系中,△ABC的三个顶点分别为A(1,2),B(2,1),C(3,2),现以原点O为位似中心,在第一象限内作与△ABC的相似比为2的位似图形△A'B'C',则顶点C'的坐标是( )
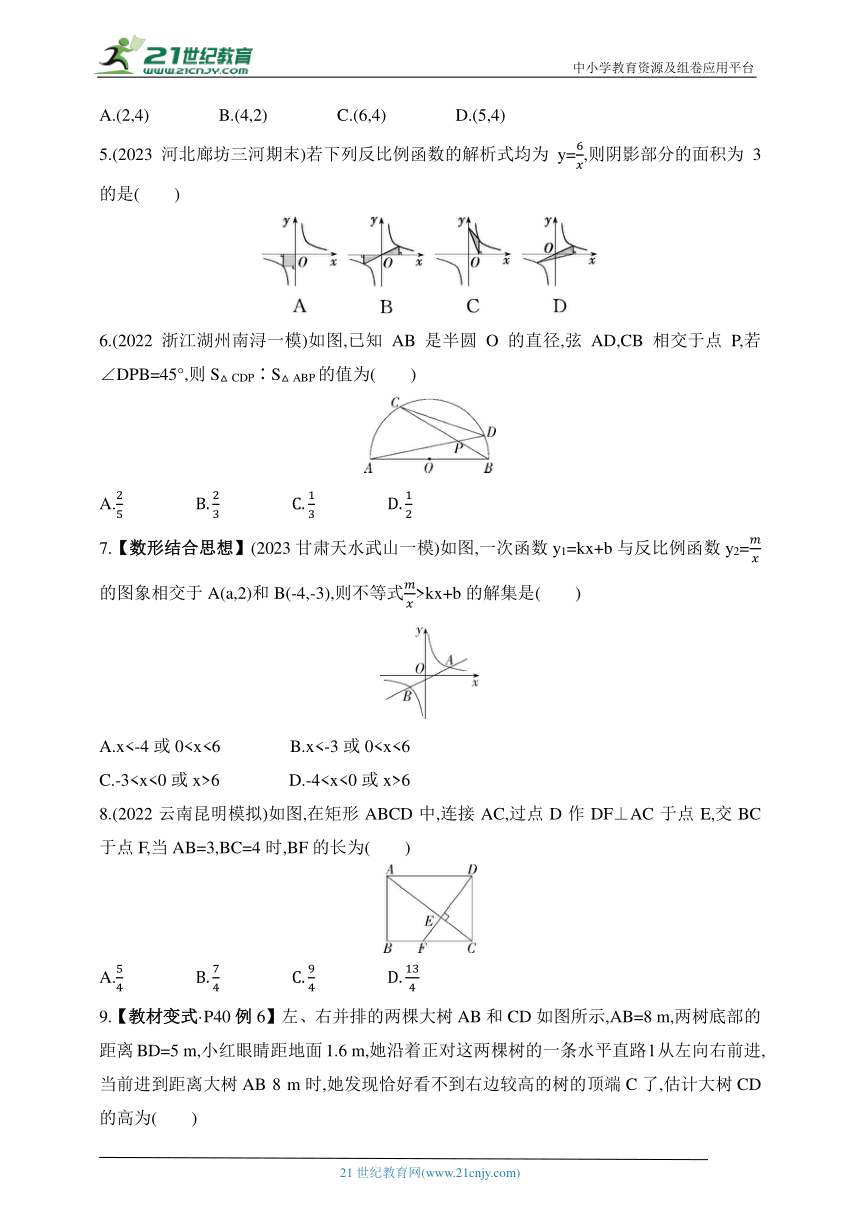
A.(2,4) B.(4,2) C.(6,4) D.(5,4)
5.(2023河北廊坊三河期末)若下列反比例函数的解析式均为y=,则阴影部分的面积为3的是( )
6.(2022浙江湖州南浔一模)如图,已知AB是半圆O的直径,弦AD,CB相交于点P,若∠DPB=45°,则S△CDP∶S△ABP的值为( )
A.
7.【数形结合思想】(2023甘肃天水武山一模)如图,一次函数y1=kx+b与反比例函数y2=的图象相交于A(a,2)和B(-4,-3),则不等式>kx+b的解集是( )
A.x<-4或0C.-36 D.-46
8.(2022云南昆明模拟)如图,在矩形ABCD中,连接AC,过点D作DF⊥AC于点E,交BC于点F,当AB=3,BC=4时,BF的长为( )
A.
9.【教材变式·P40例6】左、右并排的两棵大树AB和CD如图所示,AB=8 m,两树底部的距离BD=5 m,小红眼睛距地面1.6 m,她沿着正对这两棵树的一条水平直路l从左向右前进,当前进到距离大树AB 8 m时,她发现恰好看不到右边较高的树的顶端C了,估计大树CD的高为( )
A.18.24 m B.13 m C.12 m D.10 m
10.【三垂直模型】(2021广西北海合浦期末)如图,一块含有30°角的直角三角板的直角顶点和坐标原点O重合,30°角的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,则k的值为( )
A.-8 B.8 C.-12 D.12
二、填空题(每小题4分,共24分)
11.(2023山东淄博周村期末)函数y=(m+1)是y关于x的反比例函数,则m= .
12.【新考向·开放型试题】(2023江苏盐城东台月考)如图,AE与BD相交于点C,要使△ABC∽△DEC,需要条件 (只需写一个条件).
13.(2022上海长宁模拟)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,如果,AD=8,那么CD的长是 .
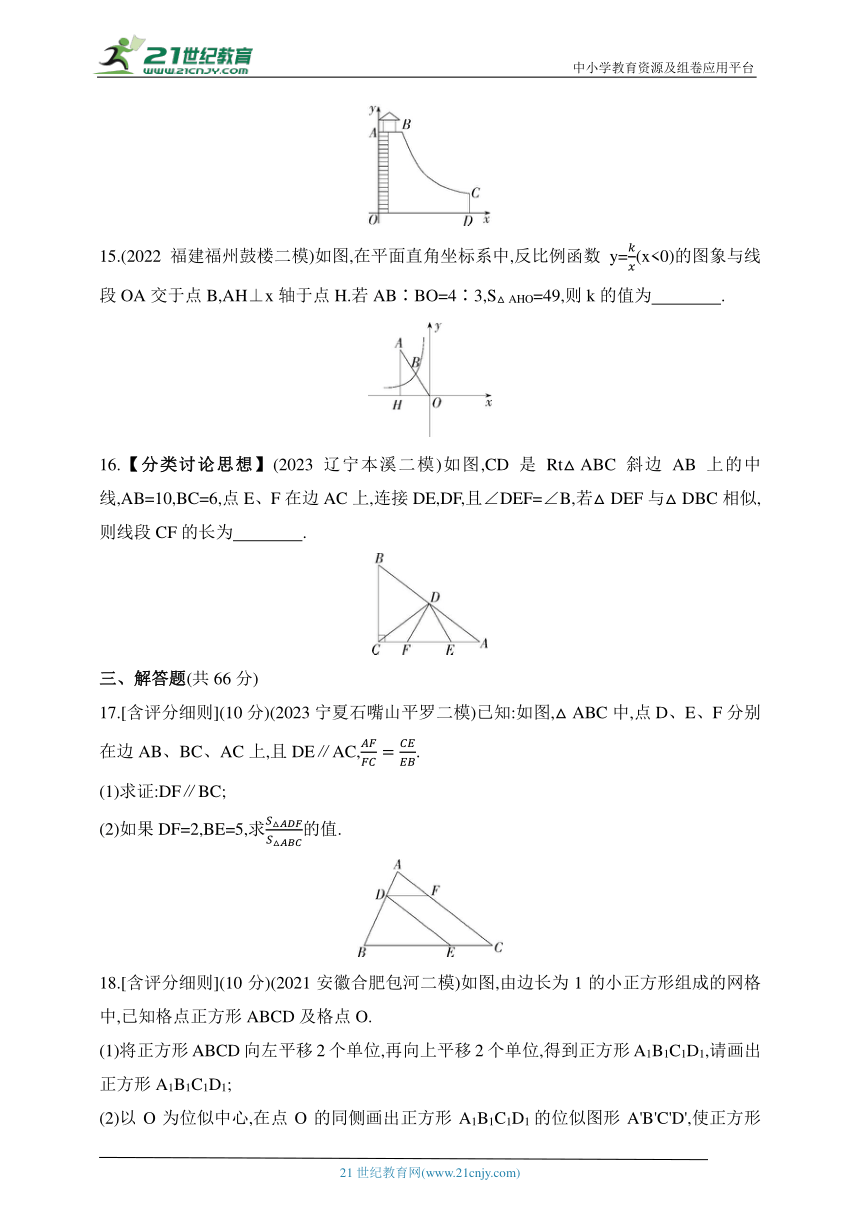
14.【新独家原创】某水上乐园“水上滑梯”的侧面图如图所示,其中BC段可看成是一段双曲线,已知竖直梯子外侧OA=5 m,进口AB∥OD,且AB=2 m,出口C点距OA的水平距离为10 m,则C点距水面的距离CD为 m.
15.(2022福建福州鼓楼二模)如图,在平面直角坐标系中,反比例函数y=(x<0)的图象与线段OA交于点B,AH⊥x轴于点H.若AB∶BO=4∶3,S△AHO=49,则k的值为 .
16.【分类讨论思想】(2023辽宁本溪二模)如图,CD是Rt△ABC斜边AB上的中线,AB=10,BC=6,点E、F在边AC上,连接DE,DF,且∠DEF=∠B,若△DEF与△DBC相似,则线段CF的长为 .
三、解答题(共66分)
17.[含评分细则](10分)(2023宁夏石嘴山平罗二模)已知:如图,△ABC中,点D、E、F分别在边AB、BC、AC上,且DE∥AC,.
(1)求证:DF∥BC;
(2)如果DF=2,BE=5,求的值.
18.[含评分细则](10分)(2021安徽合肥包河二模)如图,由边长为1的小正方形组成的网格中,已知格点正方形ABCD及格点O.
(1)将正方形ABCD向左平移2个单位,再向上平移2个单位,得到正方形A1B1C1D1,请画出正方形A1B1C1D1;
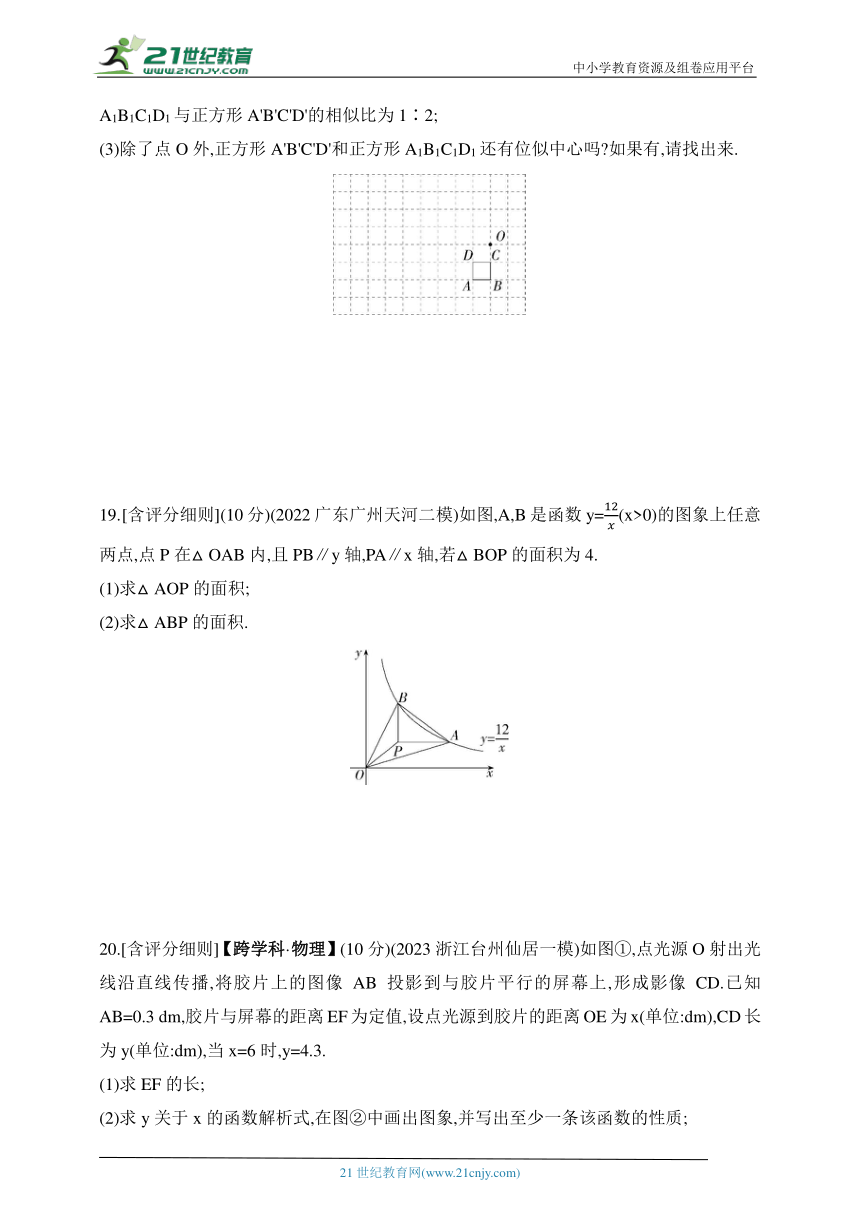
(2)以O为位似中心,在点O的同侧画出正方形A1B1C1D1的位似图形A'B'C'D',使正方形A1B1C1D1与正方形A'B'C'D'的相似比为1∶2;
(3)除了点O外,正方形A'B'C'D'和正方形A1B1C1D1还有位似中心吗 如果有,请找出来.
[含评分细则](10分)(2022广东广州天河二模)如图,A,B是函数y=(x>0)的图象上任意两点,点P在△OAB内,且PB∥y轴,PA∥x轴,若△BOP的面积为4.
(1)求△AOP的面积;
(2)求△ABP的面积.
20.[含评分细则]【跨学科·物理】(10分)(2023浙江台州仙居一模)如图①,点光源O射出光线沿直线传播,将胶片上的图像AB投影到与胶片平行的屏幕上,形成影像CD.已知AB=0.3 dm,胶片与屏幕的距离EF为定值,设点光源到胶片的距离OE为x(单位:dm),CD长为y(单位:dm),当x=6时,y=4.3.
(1)求EF的长;
(2)求y关于x的函数解析式,在图②中画出图象,并写出至少一条该函数的性质;
(3)若要求CD不小于3 dm,求OE的取值范围.
21.[含评分细则]【生命安全与健康】(12分)(2022浙江金华义乌模拟)某制药公司生产3支单针疫苗和2支双针疫苗需要19 min;生产2支单针疫苗和1支双针疫苗需要11 min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:mg/mL)与时间x(单位:天)的函数关系如图所示,疫苗注射后首先y与x成一次函数关系,体内抗体浓度到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50 mg/mL,并且不低于23 mg/mL,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.
①请写出两段函数对应的表达式,并写出自变量的取值范围;
②小明可以在哪个时间段内打第二针疫苗 请通过计算说明(精确到1天).
22.[含评分细则](14分)(2022四川绵阳游仙模拟)如图,在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(2,3),B(6,a),直线l:y=mx+n经过A,B两点,且分别交x轴,y轴于D,C两点.
(1)当>mx+n时,直接写出x的取值范围;
(2)求反比例函数与直线l的解析式;
(3)在y轴上是否存在一点E,使得以A,C,E为顶点的三角形与△CDO相似 若存在,请求出点E的坐标;若不存在,请说明理由.
答案全解全析
1.B 选项A,任意两个等边三角形的角相等,边成比例,相似,该命题为真命题;选项B,两边成比例且夹角相等的两个三角形相似,任意一角相等时不一定相似,该命题为假命题;选项C,相似多边形周长的比等于相似比,该命题为真命题;选项D,相似三角形面积的比等于相似比的平方,该命题为真命题.故选B.
2.A ∵反比例函数图象在点(2,4)和(4,4)之间,∴2×43.C 选项A,∵k=-6<0,∴函数图象的两个分支分别位于第二、四象限,原说法错误;选项B,∵2×3=6≠-6,∴点(2,3)不在该函数图象上,原说法错误;选项C,当x<0时,函数图象位于第二象限,y随x的增大而增大,原说法正确;选项D,当y≥-2时,x≥3或x<0,原说法错误.故选C.
4.C ∵△ABC与△A'B'C'关于点O位似,△A'B'C'与△ABC的相似比为2,点C的坐标为(3,2),△A'B'C'与△ABC在点O的同侧,∴点C'的坐标为(3×2,2×2),即(6,4).故选C.
5.C 选项A,阴影面积=|6|=6;选项B,阴影面积=×|6|=6;选项C,阴影面积=×|6|=3;选项D,阴影面积=2××|6|=6.故选C.
6.D 如图,连接DB,∵AB是直径,∴∠ADB=90°.∵∠DPB=45°,∴∠DPB=∠DBP=45°,∴DP=DB,∴PB=DP.∵∠C=∠A,∠CDP=∠ABP,∴△CDP∽△ABP,∴.故选D.
7.A ∵B(-4,-3)在反比例函数y2=的图象上,∴m=-4×(-3)=12,即反比例函数的解析式为y2=.∵A(a,2)在y2=的图象上,∴a==6,即A(6,2).观察图象知,不等式>kx+b的解集是x<-4或08.B ∵四边形ABCD是矩形,∴∠B=∠ADC=∠BCD=90°,∴AC==5.∵DE⊥AC,∴∠DEC=∠ADC=90°.
∵∠ACD=∠DCE,∴△CAD∽△CDE,∴,即,
∴DE=.∵∠DEC=∠DCF=90°,∠CDE=∠FDC,∴△CDE∽△FDC,∴,即.故选B.
9.C 如图,当小红的眼睛的位置到F'时,C,A,F'共线,此时小红恰好看不到树CD的顶端C了.∵AB⊥l,CD⊥l,∴AB∥CD,∴△F'AH∽△F'CK,∴F'H∶F'K=AH∶CK,∵AH=AB-BH=8-1.6=6.4(m),CK=CD-KD,F'H=8 m,F'K=F'H+HK=13(m),∴,∴CD=12(m).故选C.
10.C 如图,过点A、B分别作x轴的垂线,垂足分别为C、D,在Rt△ABO中,∠BAO=30°,∠AOB=90°,∴AB=2OB,AO=.
∵∠BOD+∠OBD=90°,∠BOD+∠AOC=180°-90°=90°,∴∠OBD=∠AOC,又∵∠ACO=∠ODB=90°,∴△AOC∽△OBD,∴.
∵点B在y=的图象上,∴S△OBD=×4=2,∴S△AOC=3S△OBD=3×2=6=|k|,
∴k=±12,
又∵点A在第二象限,∴k=-12.
故选C.
11.2
解析 ∵函数y=(m+1)是y关于x的反比例函数,∴解得m=2.
12.∠A=∠D
解析 ①添加∠A=∠D,∵∠A=∠D,∠ACB=∠DCE,∴△ABC∽△DEC;②添加∠B=∠E,∵∠B=∠E,∠ACB=∠DCE,∴△ABC∽△DEC;③添加,∠ACB=∠DCE,∴△ABC∽△DEC.
13.
解析 ∵∠ACB=90°,∴∠ACD+∠BCD=90°.∵CD⊥AB,∴∠A+∠ACD=90°,∴∠A=∠BCD,又∠ADC=∠CDB,∴△ADC∽△CDB,∴,即,解得CD=.
14.1
解析 如图,作BE⊥OD于E,∵OA=5 m,AB∥OD,且AB=2 m,∴四边形AOEB是矩形,∴BE=OA=5 m,∴B(2,5).设双曲线的解析式为y=,则k=2×5=10,∴y=.∵OD=10 m,当x=10时,y=1,∴CD=1 m.
15.-18
解析 如图,作BE⊥x轴于E,∵AH⊥x轴,∴BE∥AH,∴△BOE∽△AOH,∴.∵AB∶BO=4∶3,∴AO∶BO=7∶3,∵S△AHO=49,∴S△BOE=9.∵S△BOE=|k|,k<0,∴k=-18.
16.
解析 ∵CD是Rt△ABC斜边AB上的中线,AB=10,∴CD==8.△BDC是等腰三角形,∠BDC为顶角,∠B为底角,∠DEF=∠B,所以△DEF与△DBC相似时,△DEF也是等腰三角形,∠DEF为底角,则∠EDF或∠DFE为顶角.当△BDC∽△EDF时,∵CD=BD,∴DE=DF,∴∠DFE=∠DEF,∴∠DFC=∠DEA,∵CD=DA,∴∠DCA=∠A,∴△DFC≌△DEA(AAS),∴CF=AE,∵∠DEF=∠B,∠A+∠B=90°,∴∠DCA+∠DEF=90°,∴∠CDE=90°,∴∠CDE=∠ACB,∵∠DCE=∠A,∴△DCE∽△CAB,∴;当△BDC∽△EFD时,∠DFE=∠BDC,∵∠DFE=∠FCD+∠FDC,∠BDC=∠FCD+∠A,∴∠FDC=∠A,∵∠DCF=∠ACD,∴△DFC∽△ADC,∴.综上所述,CF的长为.
17.解析 (1)证明:∵DE∥AC,∴.
∵,
∴.2分
∵∠A=∠A,∴△ADF∽△ABC,3分
∴∠ADF=∠ABC,∴DF∥BC.5分
(2)∵DE∥AC,DF∥BC,
∴四边形DECF是平行四边形,6分
∴EC=DF=2,∴BC=BE+EC=7.7分
又由(1)得△ADF∽△ABC,8分
∴.10分
18.解析 (1)如图,正方形A1B1C1D1为所作.3分
(2)如图,正方形A'B'C'D'为所作.6分
(3)除了点O外,正方形A'B'C'D'和正方形A1B1C1D1还有位似中心,8分
如图,点P为位似中心.10分
19.解析 (1)如图,延长BP交x轴于点Q,延长AP交y轴于点M,
∵PB∥y轴,PA∥x轴,点A,B在函数y=(x>0)的图象上,
∴S△BOQ=S△AOM=×12=6,3分
又∵△BOP的面积为4,∴S△POQ=6-4=2=S△POM,
∴S△AOP=S△AOM-S△POM=6-2=4.5分
(2)∵S△POM=2,S△AOP=4,
∴AP=2PM=2OQ.7分
∵S△POQ=2,S△BOP=4,∴PB=2PQ,
∴S△ABP=×AP×BP=2OQ·PQ=4S△POQ=8.10分
20.解析 (1)∵AB∥CD,
∴△OAB∽△OCD,1分
∴,解得EF=80,
答:EF的长为80 dm.3分
(2)由(1)得,4分
∴y=0.3+,5分
图象如图.6分
性质:当x>0时,y随x的增大而减小.7分
(注:写出其他性质,只要合理均可给分)
(3)令y≥3,得0.3+≥3(x>0),8分
则0.3x+24≥3x,解得x≤,
∴OE的取值范围为0 dm21.解析 (1)设生产1支单针疫苗需要m min,生产1支双针疫苗需要n min.
根据题意,得1分
解得2分
答:生产1支单针疫苗需要3 min,生产1支双针疫苗需要5 min.4分
(2)①设一次函数解析式为y=kx,将(0.7,910)代入,解得k=1 300,故y=1 300x.6分
设反比例函数解析式为y=,将(0.7,910)代入,
解得k1=637,故y=.8分
∴两段函数对应的表达式分别为y=1 300x(0≤x≤0.7),y=(x>0.7).9分
②对于y=,当y=50时,x=12.74,
当y=23时,x≈27.7,10分
可知当23≤y≤50时,12.74≤x≤27.7,
所以小明打第二针疫苗的时间段为打第一针后的第13天到第27天.12分
22.解析 (1)由图象知,当>mx+n时,x的取值范围为06.3分
(2)将A(2,3)代入y=得,k=2×3=6,
∴反比例函数的解析式为y=.5分
将B(6,a)代入y=,得a=1,∴B(6,1).6分
再将A(2,3),B(6,1)代入y=mx+n,得
∴直线l的解析式为y=-x+4.8分
(3)存在,①如图,当△COD∽△CEA时,
可得∠CEA=∠COD=90°,
∵直线l的解析式为y=-x+4,
∴C(0,4),D(8,0).9分
∵△COD∽△CEA,∴,
∴,∴CE=1,∴E(0,3).10分
②如图,当△COD∽△CAE时,作AH⊥y轴于H,
则AH=2,
∵∠CEA=∠CDO,∠AHE=∠COD,
∴△COD∽△AHE,12分
∴,
∴HE=4,∴E(0,-1).
综上,E的坐标为(0,3)或(0,-1).14分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
期中素养综合测试
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.【新独家原创】以下命题为假命题的是( )
A.任意两个等边三角形都相似
B.两边成比例且一角相等的两个三角形相似
C.相似多边形周长的比等于相似比
D.相似三角形面积的比等于相似比的平方
2.(2023河北保定莲池三模)如图,函数y=在第一象限的图象将所标的三个整点分隔开,则整数k的值可能是( )
A.10
B.8
C.7
D.6
3.(2023湖北武汉新洲模拟)已知反比例函数表达式为y=-,则下列说法正确的是( )
A.函数图象位于第一、三象限
B.点(2,3)在该函数图象上
C.当x<0时,y随x的增大而增大
D.当y≥-2时,x≥3
4.(2023浙江嘉兴中考)如图,在直角坐标系中,△ABC的三个顶点分别为A(1,2),B(2,1),C(3,2),现以原点O为位似中心,在第一象限内作与△ABC的相似比为2的位似图形△A'B'C',则顶点C'的坐标是( )
A.(2,4) B.(4,2) C.(6,4) D.(5,4)
5.(2023河北廊坊三河期末)若下列反比例函数的解析式均为y=,则阴影部分的面积为3的是( )
6.(2022浙江湖州南浔一模)如图,已知AB是半圆O的直径,弦AD,CB相交于点P,若∠DPB=45°,则S△CDP∶S△ABP的值为( )
A.
7.【数形结合思想】(2023甘肃天水武山一模)如图,一次函数y1=kx+b与反比例函数y2=的图象相交于A(a,2)和B(-4,-3),则不等式>kx+b的解集是( )
A.x<-4或0
8.(2022云南昆明模拟)如图,在矩形ABCD中,连接AC,过点D作DF⊥AC于点E,交BC于点F,当AB=3,BC=4时,BF的长为( )
A.
9.【教材变式·P40例6】左、右并排的两棵大树AB和CD如图所示,AB=8 m,两树底部的距离BD=5 m,小红眼睛距地面1.6 m,她沿着正对这两棵树的一条水平直路l从左向右前进,当前进到距离大树AB 8 m时,她发现恰好看不到右边较高的树的顶端C了,估计大树CD的高为( )
A.18.24 m B.13 m C.12 m D.10 m
10.【三垂直模型】(2021广西北海合浦期末)如图,一块含有30°角的直角三角板的直角顶点和坐标原点O重合,30°角的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,则k的值为( )
A.-8 B.8 C.-12 D.12
二、填空题(每小题4分,共24分)
11.(2023山东淄博周村期末)函数y=(m+1)是y关于x的反比例函数,则m= .
12.【新考向·开放型试题】(2023江苏盐城东台月考)如图,AE与BD相交于点C,要使△ABC∽△DEC,需要条件 (只需写一个条件).
13.(2022上海长宁模拟)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,如果,AD=8,那么CD的长是 .
14.【新独家原创】某水上乐园“水上滑梯”的侧面图如图所示,其中BC段可看成是一段双曲线,已知竖直梯子外侧OA=5 m,进口AB∥OD,且AB=2 m,出口C点距OA的水平距离为10 m,则C点距水面的距离CD为 m.
15.(2022福建福州鼓楼二模)如图,在平面直角坐标系中,反比例函数y=(x<0)的图象与线段OA交于点B,AH⊥x轴于点H.若AB∶BO=4∶3,S△AHO=49,则k的值为 .
16.【分类讨论思想】(2023辽宁本溪二模)如图,CD是Rt△ABC斜边AB上的中线,AB=10,BC=6,点E、F在边AC上,连接DE,DF,且∠DEF=∠B,若△DEF与△DBC相似,则线段CF的长为 .
三、解答题(共66分)
17.[含评分细则](10分)(2023宁夏石嘴山平罗二模)已知:如图,△ABC中,点D、E、F分别在边AB、BC、AC上,且DE∥AC,.
(1)求证:DF∥BC;
(2)如果DF=2,BE=5,求的值.
18.[含评分细则](10分)(2021安徽合肥包河二模)如图,由边长为1的小正方形组成的网格中,已知格点正方形ABCD及格点O.
(1)将正方形ABCD向左平移2个单位,再向上平移2个单位,得到正方形A1B1C1D1,请画出正方形A1B1C1D1;
(2)以O为位似中心,在点O的同侧画出正方形A1B1C1D1的位似图形A'B'C'D',使正方形A1B1C1D1与正方形A'B'C'D'的相似比为1∶2;
(3)除了点O外,正方形A'B'C'D'和正方形A1B1C1D1还有位似中心吗 如果有,请找出来.
[含评分细则](10分)(2022广东广州天河二模)如图,A,B是函数y=(x>0)的图象上任意两点,点P在△OAB内,且PB∥y轴,PA∥x轴,若△BOP的面积为4.
(1)求△AOP的面积;
(2)求△ABP的面积.
20.[含评分细则]【跨学科·物理】(10分)(2023浙江台州仙居一模)如图①,点光源O射出光线沿直线传播,将胶片上的图像AB投影到与胶片平行的屏幕上,形成影像CD.已知AB=0.3 dm,胶片与屏幕的距离EF为定值,设点光源到胶片的距离OE为x(单位:dm),CD长为y(单位:dm),当x=6时,y=4.3.
(1)求EF的长;
(2)求y关于x的函数解析式,在图②中画出图象,并写出至少一条该函数的性质;
(3)若要求CD不小于3 dm,求OE的取值范围.
21.[含评分细则]【生命安全与健康】(12分)(2022浙江金华义乌模拟)某制药公司生产3支单针疫苗和2支双针疫苗需要19 min;生产2支单针疫苗和1支双针疫苗需要11 min.
(1)制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间
(2)小明选择注射双针疫苗,若注射第一针疫苗后,体内抗体浓度y(单位:mg/mL)与时间x(单位:天)的函数关系如图所示,疫苗注射后首先y与x成一次函数关系,体内抗体浓度到达峰值后,y与x成反比例函数关系.若体内抗体浓度不高于50 mg/mL,并且不低于23 mg/mL,可以打第二针疫苗,刺激记忆细胞增殖分化,产生大量浆细胞而产生更多的抗体.
①请写出两段函数对应的表达式,并写出自变量的取值范围;
②小明可以在哪个时间段内打第二针疫苗 请通过计算说明(精确到1天).
22.[含评分细则](14分)(2022四川绵阳游仙模拟)如图,在平面直角坐标系xOy中,反比例函数y=(x>0)的图象经过点A(2,3),B(6,a),直线l:y=mx+n经过A,B两点,且分别交x轴,y轴于D,C两点.
(1)当>mx+n时,直接写出x的取值范围;
(2)求反比例函数与直线l的解析式;
(3)在y轴上是否存在一点E,使得以A,C,E为顶点的三角形与△CDO相似 若存在,请求出点E的坐标;若不存在,请说明理由.
答案全解全析
1.B 选项A,任意两个等边三角形的角相等,边成比例,相似,该命题为真命题;选项B,两边成比例且夹角相等的两个三角形相似,任意一角相等时不一定相似,该命题为假命题;选项C,相似多边形周长的比等于相似比,该命题为真命题;选项D,相似三角形面积的比等于相似比的平方,该命题为真命题.故选B.
2.A ∵反比例函数图象在点(2,4)和(4,4)之间,∴2×4
4.C ∵△ABC与△A'B'C'关于点O位似,△A'B'C'与△ABC的相似比为2,点C的坐标为(3,2),△A'B'C'与△ABC在点O的同侧,∴点C'的坐标为(3×2,2×2),即(6,4).故选C.
5.C 选项A,阴影面积=|6|=6;选项B,阴影面积=×|6|=6;选项C,阴影面积=×|6|=3;选项D,阴影面积=2××|6|=6.故选C.
6.D 如图,连接DB,∵AB是直径,∴∠ADB=90°.∵∠DPB=45°,∴∠DPB=∠DBP=45°,∴DP=DB,∴PB=DP.∵∠C=∠A,∠CDP=∠ABP,∴△CDP∽△ABP,∴.故选D.
7.A ∵B(-4,-3)在反比例函数y2=的图象上,∴m=-4×(-3)=12,即反比例函数的解析式为y2=.∵A(a,2)在y2=的图象上,∴a==6,即A(6,2).观察图象知,不等式>kx+b的解集是x<-4或0
∵∠ACD=∠DCE,∴△CAD∽△CDE,∴,即,
∴DE=.∵∠DEC=∠DCF=90°,∠CDE=∠FDC,∴△CDE∽△FDC,∴,即.故选B.
9.C 如图,当小红的眼睛的位置到F'时,C,A,F'共线,此时小红恰好看不到树CD的顶端C了.∵AB⊥l,CD⊥l,∴AB∥CD,∴△F'AH∽△F'CK,∴F'H∶F'K=AH∶CK,∵AH=AB-BH=8-1.6=6.4(m),CK=CD-KD,F'H=8 m,F'K=F'H+HK=13(m),∴,∴CD=12(m).故选C.
10.C 如图,过点A、B分别作x轴的垂线,垂足分别为C、D,在Rt△ABO中,∠BAO=30°,∠AOB=90°,∴AB=2OB,AO=.
∵∠BOD+∠OBD=90°,∠BOD+∠AOC=180°-90°=90°,∴∠OBD=∠AOC,又∵∠ACO=∠ODB=90°,∴△AOC∽△OBD,∴.
∵点B在y=的图象上,∴S△OBD=×4=2,∴S△AOC=3S△OBD=3×2=6=|k|,
∴k=±12,
又∵点A在第二象限,∴k=-12.
故选C.
11.2
解析 ∵函数y=(m+1)是y关于x的反比例函数,∴解得m=2.
12.∠A=∠D
解析 ①添加∠A=∠D,∵∠A=∠D,∠ACB=∠DCE,∴△ABC∽△DEC;②添加∠B=∠E,∵∠B=∠E,∠ACB=∠DCE,∴△ABC∽△DEC;③添加,∠ACB=∠DCE,∴△ABC∽△DEC.
13.
解析 ∵∠ACB=90°,∴∠ACD+∠BCD=90°.∵CD⊥AB,∴∠A+∠ACD=90°,∴∠A=∠BCD,又∠ADC=∠CDB,∴△ADC∽△CDB,∴,即,解得CD=.
14.1
解析 如图,作BE⊥OD于E,∵OA=5 m,AB∥OD,且AB=2 m,∴四边形AOEB是矩形,∴BE=OA=5 m,∴B(2,5).设双曲线的解析式为y=,则k=2×5=10,∴y=.∵OD=10 m,当x=10时,y=1,∴CD=1 m.
15.-18
解析 如图,作BE⊥x轴于E,∵AH⊥x轴,∴BE∥AH,∴△BOE∽△AOH,∴.∵AB∶BO=4∶3,∴AO∶BO=7∶3,∵S△AHO=49,∴S△BOE=9.∵S△BOE=|k|,k<0,∴k=-18.
16.
解析 ∵CD是Rt△ABC斜边AB上的中线,AB=10,∴CD==8.△BDC是等腰三角形,∠BDC为顶角,∠B为底角,∠DEF=∠B,所以△DEF与△DBC相似时,△DEF也是等腰三角形,∠DEF为底角,则∠EDF或∠DFE为顶角.当△BDC∽△EDF时,∵CD=BD,∴DE=DF,∴∠DFE=∠DEF,∴∠DFC=∠DEA,∵CD=DA,∴∠DCA=∠A,∴△DFC≌△DEA(AAS),∴CF=AE,∵∠DEF=∠B,∠A+∠B=90°,∴∠DCA+∠DEF=90°,∴∠CDE=90°,∴∠CDE=∠ACB,∵∠DCE=∠A,∴△DCE∽△CAB,∴;当△BDC∽△EFD时,∠DFE=∠BDC,∵∠DFE=∠FCD+∠FDC,∠BDC=∠FCD+∠A,∴∠FDC=∠A,∵∠DCF=∠ACD,∴△DFC∽△ADC,∴.综上所述,CF的长为.
17.解析 (1)证明:∵DE∥AC,∴.
∵,
∴.2分
∵∠A=∠A,∴△ADF∽△ABC,3分
∴∠ADF=∠ABC,∴DF∥BC.5分
(2)∵DE∥AC,DF∥BC,
∴四边形DECF是平行四边形,6分
∴EC=DF=2,∴BC=BE+EC=7.7分
又由(1)得△ADF∽△ABC,8分
∴.10分
18.解析 (1)如图,正方形A1B1C1D1为所作.3分
(2)如图,正方形A'B'C'D'为所作.6分
(3)除了点O外,正方形A'B'C'D'和正方形A1B1C1D1还有位似中心,8分
如图,点P为位似中心.10分
19.解析 (1)如图,延长BP交x轴于点Q,延长AP交y轴于点M,
∵PB∥y轴,PA∥x轴,点A,B在函数y=(x>0)的图象上,
∴S△BOQ=S△AOM=×12=6,3分
又∵△BOP的面积为4,∴S△POQ=6-4=2=S△POM,
∴S△AOP=S△AOM-S△POM=6-2=4.5分
(2)∵S△POM=2,S△AOP=4,
∴AP=2PM=2OQ.7分
∵S△POQ=2,S△BOP=4,∴PB=2PQ,
∴S△ABP=×AP×BP=2OQ·PQ=4S△POQ=8.10分
20.解析 (1)∵AB∥CD,
∴△OAB∽△OCD,1分
∴,解得EF=80,
答:EF的长为80 dm.3分
(2)由(1)得,4分
∴y=0.3+,5分
图象如图.6分
性质:当x>0时,y随x的增大而减小.7分
(注:写出其他性质,只要合理均可给分)
(3)令y≥3,得0.3+≥3(x>0),8分
则0.3x+24≥3x,解得x≤,
∴OE的取值范围为0 dm
根据题意,得1分
解得2分
答:生产1支单针疫苗需要3 min,生产1支双针疫苗需要5 min.4分
(2)①设一次函数解析式为y=kx,将(0.7,910)代入,解得k=1 300,故y=1 300x.6分
设反比例函数解析式为y=,将(0.7,910)代入,
解得k1=637,故y=.8分
∴两段函数对应的表达式分别为y=1 300x(0≤x≤0.7),y=(x>0.7).9分
②对于y=,当y=50时,x=12.74,
当y=23时,x≈27.7,10分
可知当23≤y≤50时,12.74≤x≤27.7,
所以小明打第二针疫苗的时间段为打第一针后的第13天到第27天.12分
22.解析 (1)由图象知,当>mx+n时,x的取值范围为0
(2)将A(2,3)代入y=得,k=2×3=6,
∴反比例函数的解析式为y=.5分
将B(6,a)代入y=,得a=1,∴B(6,1).6分
再将A(2,3),B(6,1)代入y=mx+n,得
∴直线l的解析式为y=-x+4.8分
(3)存在,①如图,当△COD∽△CEA时,
可得∠CEA=∠COD=90°,
∵直线l的解析式为y=-x+4,
∴C(0,4),D(8,0).9分
∵△COD∽△CEA,∴,
∴,∴CE=1,∴E(0,3).10分
②如图,当△COD∽△CAE时,作AH⊥y轴于H,
则AH=2,
∵∠CEA=∠CDO,∠AHE=∠COD,
∴△COD∽△AHE,12分
∴,
∴HE=4,∴E(0,-1).
综上,E的坐标为(0,3)或(0,-1).14分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
