2024人教版数学九年级下学期课时练--期末素养综合测试(二)(含解析)
文档属性
| 名称 | 2024人教版数学九年级下学期课时练--期末素养综合测试(二)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 873.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-03 09:19:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024人教版数学九年级下学期
期末素养综合测试(二)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
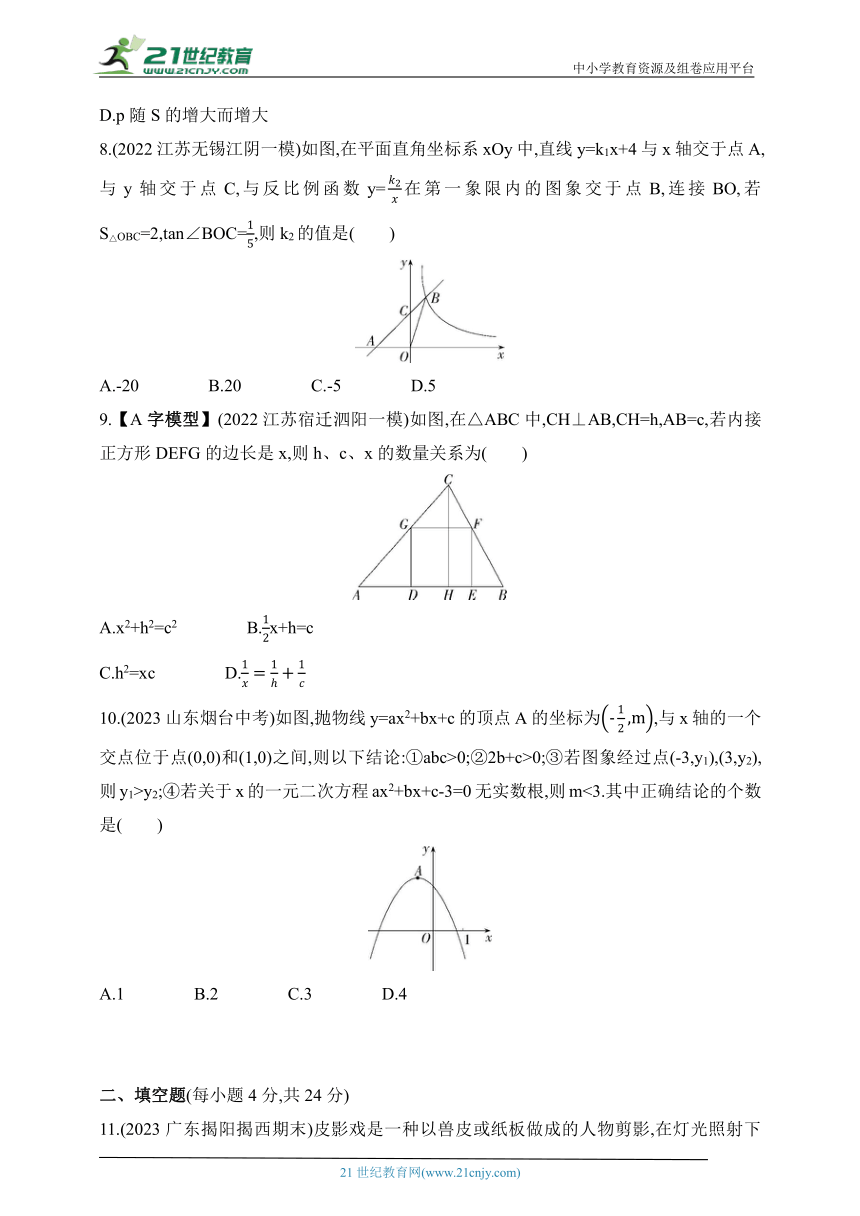
1.【数学文化】(2023湖北宜昌中考)我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形(“杨辉三角”“中国七巧板”“刘徽割圆术”“赵爽弦图”)中,中心对称图形是( )
2.【中华优秀传统文化】(2023山东枣庄中考改编)榫卯是中国古代建筑、家具及其他器械的主要结构方式,是我国工艺文化精神的传承,凸出部分叫榫,凹进部分叫卯.如图所示的是某个部件“卯”的实物图,它的俯视图是( )
3.(2022湖南常德中考)关于x的一元二次方程x2-4x+k=0无实数解,则k的取值范围是( )
A.k>4 B.k<4 C.k<-4 D.k>-4
4.【新独家原创】如图,A1B1是线段AB在投影面P上的正投影,AB=a,线段AB相对于投影面P的倾斜角为α,则投影A1B1的长为( )
A.asin α
B.acos α
C.atan α
D.
5.【新考法】(2023河北衡水二模)如图,点M,N,P,Q,T均为坐标系中2×2的正方形网格的格点(网格的横线都与x轴平行,纵线都与y轴平行,每个小正方形的边长为1个单位长度),点N的坐标为(2,2),在反比例函数y=(x>0)中的常数k的值从1逐渐增大到9的过程中,关于其图象l依次经过的格点的顺序,下列说法正确的是( )
A.点M→点P→同时经过点N,Q→点T
B.点M→点N→同时经过点P,Q→点T
C.点M→同时经过点P,Q→点N→点T
D.点P→点M→同时经过点N,Q→点T
6.(2023湖北孝感中考)如图,在☉O中,直径AB与弦CD相交于点P,连接AC,AD,BD,若∠C=20°,∠BPC=70°,则∠ADC=( )
A.70° B.60°
C.50° D.40°
7.【跨学科·物理】(2023山西晋中模拟)根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示,则下列说法正确的是( )
A.p与S的函数关系式为p=
B.当S=0.5 m2时,p=2 000 Pa
C.当S>2 m2时,p>50 Pa
D.p随S的增大而增大
8.(2022江苏无锡江阴一模)如图,在平面直角坐标系xOy中,直线y=k1x+4与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连接BO,若S△OBC=2,tan∠BOC=,则k2的值是( )
A.-20 B.20 C.-5 D.5
9.【A字模型】(2022江苏宿迁泗阳一模)如图,在△ABC中,CH⊥AB,CH=h,AB=c,若内接正方形DEFG的边长是x,则h、c、x的数量关系为( )
A.x2+h2=c2 B.x+h=c
C.h2=xc D.
10.(2023山东烟台中考)如图,抛物线y=ax2+bx+c的顶点A的坐标为,与x轴的一个交点位于点(0,0)和(1,0)之间,则以下结论:①abc>0;②2b+c>0;③若图象经过点(-3,y1),(3,y2),则y1>y2;④若关于x的一元二次方程ax2+bx+c-3=0无实数根,则m<3.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题4分,共24分)
11.(2023广东揭阳揭西期末)皮影戏是一种以兽皮或纸板做成的人物剪影,在灯光照射下用隔亮布进行表演的民间戏剧.“皮影戏”中的皮影是 (填写“平行投影”或“中心投影”).
12.(2023广东深圳中考)小明从《红星照耀中国》《红岩》《长征》《钢铁是怎样炼成的》四本书中随机挑选一本,其中拿到《红星照耀中国》这本书的概率为 .
13.(2023湖北孝感中考)已知一元二次方程x2-3x+k=0的两个实数根为x1,x2,若x1x2+2x1+2x2=1,则实数k= .
14.(2023湖南岳阳中考)2023年岳阳举办以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在A处用仪器测得赛场上一宣传气球顶部E处的仰角为21.8°,仪器与气球的水平距离AD为20米,且距地面高度AB为1.5米,则气球顶部离地面的高度EC是 米.
(结果精确到0.1米,sin 21.8°≈0.371 4,cos 21.8°≈0.928 5,tan 21.8°≈0.400 0)(M9228005)
15.【半角模型】如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,B(2,2),函数y=(x>0)的图象与边AB、BC分别交于点D、E,连接OD、OE、DE.若∠DOE=45°,则k的值为 .
16.【易错题】(2023辽宁抚顺清原三模)如图,在矩形ABCD中,AB=3,BC=6,点E是射线BC上一动点,将△ABE沿AE翻折得到△AFE,延长AF交CD的延长线于点G,当BE=3EC时,线段DG的长为 .
三、解答题(共66分)
17.[含评分细则](8分)(2022贵州贵阳中考)在初中阶段我们已经学习了一元二次方程的三种解法,它们分别是配方法、公式法和因式分解法,请从下列一元二次方程中任选两个,并解这两个方程.
①x2+2x-1=0;②x2-3x=0;③x2-4x=4;④x2-4=0.
18.[含评分细则](10分)(2023安徽马鞍山和县二模)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-3,-1),B(-4,-4),C(-1,-3).
(1)以点O为位似中心,在第一象限作出△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的相似比为1∶1;
(2)以点O为旋转中心,将△ABC顺时针旋转90°后得△A2B2C2,请作出△A2B2C2;
(3)直接写出cos∠BAC的值.
19.[含评分细则](10分)(2023四川内江市中二模)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(1,4)、B(4,n).
(1)求这两个函数的表达式;
(2)请结合图象直接写出不等式kx+b≤的解集;
(3)若点P为x轴上一点,△ABP的面积为6,求点P的坐标.
20.[含评分细则]【项目式学习试题】(12分)(2023浙江绍兴模拟)根据以下素材,探索完成任务.
如何调整足球的发球方向
某足球场的一部分如图所示,球门宽DE=CF=7 m,高CD=EF=2.51 m.小梅站在A处向门柱CD一侧发球,点A正对门柱CD(即AC⊥CF),AC=24 m,足球运动的路线是抛物线的一部分
如图,当足球运动到最高点Q时,高度为4.5 m,即QB=4.5 m,此时水平距离AB=15 m,以点A为原点,直线BA为x轴,建立平面直角坐标系
问题解决
求足球运动的高度y(m)与水平距离x(m)之间的函数关系式,并判断此时足球能否入网
小梅改变发球方向,发球时起点不变,运动路线的形状不变,判断足球能否打到远角E处入网
上述任务1、任务2中球落在球门边线视同球入网
21.[含评分细则](12分)(2022四川德阳中考)如图,AB是☉O的直径,CD是☉O的弦,AB⊥CD,垂足是点H,过点C作直线分别与AB,AD的延长线交于点E,F,且∠ECD=2∠BAD.
(1)求证:CF是☉O的切线;
(2)如果AB=10,CD=6,
①求AE的长;
②求△AEF的面积.
22.[含评分细则]【分类讨论思想】(14分)(2022四川遂宁中考)如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(-1,0),点C的坐标为(0,-3).
(1)求抛物线的解析式;
(2)【最短距离问题】如图1,E为△ABC边AB上的一动点,F为BC边上的一动点,D点坐标为(0,-2),求△DEF周长的最小值;
(3)如图2,N为射线CB上的一点,M是抛物线上的一点,M、N均在第一象限内,B、N位于直线AM的同侧,若M到x轴的距离为d,△AMN的面积为2d,当△AMN为等腰三角形时,求点N的坐标.
答案全解全析
1.D 只有选项D中图形能找到一个点,使图形绕该点旋转180°后与原来的图形重合,所以是中心对称图形.故选D.
2.B 俯视图如下:
故选B.
3.A ∵关于x的一元二次方程x2-4x+k=0无实数解,
∴Δ=(-4)2-4×1×k<0,解得k>4.故选A.
4.B 如图,过点A作AH⊥BB1于点H,则四边形AHB1A1是矩形,∴AH=A1B1,∠BAH=α.在Rt△ABH中,∵cos α=,∴AH=acos α,∴A1B1=acos α.故选B.
5.C 由题得N(2,2),M(1,2),Q(1,3),T(2,3),P(3,1),∵2×2=4,1×2=2,1×3=3,2×3=6,3×1=3,2<3=3<4<6,∴常数k的值从1逐渐增大到9的过程中,图象l依次经过的格点的顺序是点M→同时经过点P,Q→点N→点T,故选C.
6.D ∵∠C=20°,∠BPC=70°,∴∠BAC=∠BPC-∠C=50°=∠BDC,∵AB是☉O的直径,∴∠ADB=90°,∴∠ADC=∠ADB-∠BDC=40°.故选D.
7.A 选项A,设p=,∵点(0.2,500)在这个函数的图象上,∴500=,∴k=100,∴p与S的函数关系式为p=,原说法正确;选项B,当S=0.5 m2时,p==200 Pa,原说法不正确;选项C,当S>2 m2时,p<50 Pa,原说法不正确;选项D,p随S的增大而减小,原说法不正确.故选A.
8.D ∵直线y=k1x+4与y轴交于点C,∴点C的坐标为(0,4),∴OC=4.如图,过B作BD⊥y轴于D,∵S△OBC=2,∴BD=1,∵tan∠BOC=,∴OD=5,∴点B的坐标为(1,5),∵点B在反比例函数y=的图象上,∴k2=1×5=5.故选D.
9.D 如图,设CH与GF交于点M,∵四边形DEFG是正方形,∴GF∥DE,∠GDE=∠DGF=90°,∴△CGF∽△CAB,∴.∵CH⊥AB,∴∠DHM=90°,∴四边形DHMG是矩形,∴DG=MH,∵CH=h,正方形DEFG的边长是x,∴MH=x,CM=CH-MH=h-x,又AB=c,∴.故选D.
10.C ①∵抛物线y=ax2+bx+c的顶点A的坐标为<0,∴ab>0,又当x=0时,y=c>0,∴abc>0,故①正确,符合题意;②∵直线x=-是抛物线的对称轴,∴-,∴a=b,由图象可得x=1时,y=a+b+c<0,∴2b+c<0,故②错误,不合题意;③设(-3,y1),(3,y2)两点到直线x=-的距离分别为d1、d2,则d1=,∴d2>d1,根据图象可得,抛物线上的点距离对称轴越近,对应的函数值越大,∴y1>y2,故③正确,符合题意;④∵关于x的一元二次方程ax2+bx+c-3=0无实数根,∴Δ=b2-4a(c-3)<0,∴b2-4ac+12a<0,∴b2-4ac<-12a,∴4ac-b2>12a,∵m=,且由抛物线开口向下知a<0,∴m<3,故④正确,符合题意.故选C.
11.中心投影
解析 “皮影戏”中的皮影是在灯光照射下形成的影子,是中心投影.
12.
13.-5
解析 ∵一元二次方程x2-3x+k=0的两个实数根为x1,x2,∴x1+x2=3,x1·x2=k,∵x1x2+2x1+2x2=1,∴k+2×3=1,解得k=-5.∵方程有两个实数根,∴Δ=b2-4ac=(-3)2-4k≥0,解得k≤,∴k=-5符合题意.
14.9.5
解析 由题意,得四边形ABCD是矩形,∴AB=CD=1.5 m.在Rt△ADE中,∵∠EAD=21.8°,AD=20 m,∴DE=AD·tan 21.8°≈20×0.400 0=8(m),∴CE=CD+DE=1.5+8=9.5(m),即气球顶部离地面的高度EC约是9.5 m.
15.-4+4
解析 如图,延长BC至F,使得CF=AD,连接OF.∵四边形OABC是正方形,∴∠OAD=∠OCF=∠AOC=90°.在△OAD和△OCF中,CF=AD,∠OAD=∠OCF,OA=OC,∴△OAD≌△OCF(SAS),∴OF=OD,∠COF=∠AOD.∵∠DOE=45°,∴∠AOD+∠COE=45°,∴∠COF+∠COE=45°,即∠EOF=45°,∴∠EOF=∠DOE.在△DOE和△FOE中,OD=OF,∠DOE=∠EOF,OE=OE,∴△DOE≌△FOE(SAS),∴DE=EF.∵B(2,2),∴OA=OC=AB=BC=2.∵D、E在函数y=(x>0)的图象上,∴k=2AD=2CE,∴AD=CE.设AD=CE=x,则BE=BD=2-x,DE=2x.在Rt△BDE中,BD2+BE2=DE2,∴2(2-x)2=(2x)2,解得x1=-2-2(不合题意,舍去),x2=-2+2.
模型解读 半角模型:由一个大角和它的一半小角组成的共顶点且大角两边相等的基本几何模型.常见的半角模型有“45°半角模型”“60°半角模型”,基本图形如下:
解半角模型的一般步骤:①找旋转中心(含半角的角的顶点),构造旋转;②证全等;③利用全等得到边角关系.
16.或8
解析 如图①,当点E在线段BC上时,设EF交AD于K.∵BC=6,BE=3EC,∴EC=,∵四边形ABCD是矩形,∴∠ADC=∠ADG=90°,AD∥BC,∴∠DAE=∠AEB=∠AEK,∴AK=EK,设AK=EK=x,∵∠AFK=∠B=90°,AF=AB=3,FK=,∵tan∠DAG=.如图②,当点E在线段BC的延长线上时,设EF交AD于K.∵BC=6,BE=3EC,∴EC=3,EB=EF=9.∵四边形ABCD是矩形,∴∠ADC=∠ADG=90°,AD∥BC,∴∠DAE=∠AEB=∠AEK,∴AK=EK,设AK=EK=y,∵∠AFK=90°,AF=AB=3,FK=9-y,∴y2=32+(9-y)2,∴y=5,∴FK=EF-EK=4,∵tan∠DAG=,∴DG=8.
易错点 易忽视点E在BC的延长线上的情况.
17.解析 ①利用公式法:x2+2x-1=0,
Δ=22-4×1×(-1)=4+4=8,
∴x=.
∴x1=-1+.
②利用因式分解法:x2-3x=0,
∴x(x-3)=0.
∴x1=0,x2=3.
③利用配方法:x2-4x=4,
两边都加上4,得x2-4x+4=8,
∴(x-2)2=8.∴x-2=±2.
∴x1=2+2.
④利用因式分解法:x2-4=0,
∴(x+2)(x-2)=0.
∴x1=-2,x2=2.
(注:任选两个即可,每个4分,共8分)
18.解析 (1)如图,△A1B1C1为所作.3分
(2)如图,△A2B2C2为所作.6分
(3)cos∠BAC=.10分
详解:∵AB=,
∴AB=BC.如图,取AC的中点D,
则BD⊥AC,
在Rt△ABD中,∵AD=,
∴cos∠BAD=.
19.解析 (1)把A(1,4)代入y=,得m=4,
∴反比例函数的表达式为y=.2分
把B(4,n)代入y=,得n=1,
∴B(4,1).3分
把(1,4)、(4,1)代入y=kx+b,
得
∴一次函数的表达式为y=-x+5.5分
(2)不等式kx+b≤的解集为0(3)如图,设直线AB与x轴交于点C,
则点C的坐标为(5,0).8分
∵△ABP的面积为6,
∴PC×1=6,
∴PC=4,9分
∴点P的坐标为(1,0)或(9,0).10分
20.解析 任务1:由题意,得抛物线顶点坐标为,1分
设抛物线解析式为y=a(x+15)2+,2分
∵抛物线经过点A(0,0),∴225a+=0,
解得a=-,3分
∴y=-,
∴足球运动的高度y(m)与水平距离x(m)之间的函数表达式为y=-.4分
当x=-24时,y=-=2.88>2.51,
∴足球不能入网.6分
任务2:足球运动路线形状不变,连接AF,此时以点A为原点,AF所在直线为x轴,以过点A的铅垂线为y轴建立平面直角坐标系,易得抛物线的函数关系式仍为y=-.8分
∵FC=7,AC=24,∠FCA=90°,
∴AF==25,10分
当x=-25时,y=2.5<2.51,
∴能打到远角E处入网.12分
21.解析 (1)证明:连接OC,如图,
∵AB是☉O的直径,AB⊥CD,
∴.∴∠CAB=∠DAB.
∵∠COB=2∠CAB,∴∠COB=2∠BAD.
∵∠ECD=2∠BAD,∴∠ECD=∠COB.2分
∵AB⊥CD,∴∠COB+∠OCH=90°,
∴∠OCH+∠ECD=90°,∴∠OCE=90°.
∴OC⊥CF.3分
∵OC是☉O的半径,
∴CF是☉O的切线.4分
(2)①∵AB=10,∴OA=OB=OC=5,
∵AB是☉O的直径,AB⊥CD,
∴CH=DH=CD=3.
∴OH==4,6分
∵OC⊥CF,CH⊥OE,∴△OCH∽△OEC,
∴.
∴AE=OA+OE=5+.8分
②过点F作FG⊥AB,交AB的延长线于点G,如图,
∵∠OCF=∠FGE=90°,∠CEO=∠GEF,
∴△OCE∽△FGE,
∴,10分
设FG=4k,则FE=5k,∴EG==3k,
∵DH⊥AB,FG⊥AB,∴DH∥FG.
∴,
解得k=.11分
∴FG=4k=5.
∴△AEF的面积=×AE·FG=.12分
22.解析 (1)∵抛物线y=x2+bx+c经过点A(-1,0),点C(0,-3).
∴
∴抛物线的解析式为y=x2-2x-3.3分
(2)如图,设D1为D关于直线AB的对称点,D2为D关于直线BC的对称点,连接D1E,D2F,D1D2,DD2,CD2.
由对称性可知DE=D1E,DF=D2F,△DEF的周长=D1E+EF+D2F,
∴当D1,E,F,D2共线时,△DEF的周长最小,最小值为D1D2的长,4分
令y=0,则x2-2x-3=0,解得x=-1或3,
∴B(3,0),∴OB=OC=3,
∴△BOC是等腰直角三角形,5分
∵BC垂直平分DD2,且D(0,-2),C(0,-3),
∴D2(1,-3),6分
∵D,D1关于x轴对称,∴D1(0,2),
∴D1D2=,
∴△DEF的周长的最小值为.7分
(3)如图,连接BM.
∵M到x轴的距离为d,AB=4,∴S△ABM=2d,
又∵S△AMN=2d,∴S△ABM=S△AMN,
∴B,N到AM的距离相等,8分
∵B,N在AM的同侧,∴AM∥BN,
设直线BC的解析式为y=kx+m,
则有
∴直线BC的解析式为y=x-3,9分
∵A(-1,0),AM∥BC,
∴直线AM的解析式为y=x+1,
由
∴M(4,5),10分
∵点N在射线CB上,∴设N(t,t-3),
过点M作x轴的平行线l,过点N作y轴的平行线交x轴于点P,交直线l于点Q.
∵A(-1,0),M(4,5),N(t,t-3),
∴AM=5,
MN=.11分
当AM=AN时,5,
解得t=1±,
当AM=MN时,5,
解得t=6±,
当AN=MN时,
,
解得t=,
∵N在第一象限,∴t>3,
∴t的值为或1+或6+,
∴点N的坐标为或(1+)或(6+).14分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024人教版数学九年级下学期
期末素养综合测试(二)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.【数学文化】(2023湖北宜昌中考)我国古代数学的许多创新与发明都曾在世界上有重要影响.下列图形(“杨辉三角”“中国七巧板”“刘徽割圆术”“赵爽弦图”)中,中心对称图形是( )
2.【中华优秀传统文化】(2023山东枣庄中考改编)榫卯是中国古代建筑、家具及其他器械的主要结构方式,是我国工艺文化精神的传承,凸出部分叫榫,凹进部分叫卯.如图所示的是某个部件“卯”的实物图,它的俯视图是( )
3.(2022湖南常德中考)关于x的一元二次方程x2-4x+k=0无实数解,则k的取值范围是( )
A.k>4 B.k<4 C.k<-4 D.k>-4
4.【新独家原创】如图,A1B1是线段AB在投影面P上的正投影,AB=a,线段AB相对于投影面P的倾斜角为α,则投影A1B1的长为( )
A.asin α
B.acos α
C.atan α
D.
5.【新考法】(2023河北衡水二模)如图,点M,N,P,Q,T均为坐标系中2×2的正方形网格的格点(网格的横线都与x轴平行,纵线都与y轴平行,每个小正方形的边长为1个单位长度),点N的坐标为(2,2),在反比例函数y=(x>0)中的常数k的值从1逐渐增大到9的过程中,关于其图象l依次经过的格点的顺序,下列说法正确的是( )
A.点M→点P→同时经过点N,Q→点T
B.点M→点N→同时经过点P,Q→点T
C.点M→同时经过点P,Q→点N→点T
D.点P→点M→同时经过点N,Q→点T
6.(2023湖北孝感中考)如图,在☉O中,直径AB与弦CD相交于点P,连接AC,AD,BD,若∠C=20°,∠BPC=70°,则∠ADC=( )
A.70° B.60°
C.50° D.40°
7.【跨学科·物理】(2023山西晋中模拟)根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示,则下列说法正确的是( )
A.p与S的函数关系式为p=
B.当S=0.5 m2时,p=2 000 Pa
C.当S>2 m2时,p>50 Pa
D.p随S的增大而增大
8.(2022江苏无锡江阴一模)如图,在平面直角坐标系xOy中,直线y=k1x+4与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连接BO,若S△OBC=2,tan∠BOC=,则k2的值是( )
A.-20 B.20 C.-5 D.5
9.【A字模型】(2022江苏宿迁泗阳一模)如图,在△ABC中,CH⊥AB,CH=h,AB=c,若内接正方形DEFG的边长是x,则h、c、x的数量关系为( )
A.x2+h2=c2 B.x+h=c
C.h2=xc D.
10.(2023山东烟台中考)如图,抛物线y=ax2+bx+c的顶点A的坐标为,与x轴的一个交点位于点(0,0)和(1,0)之间,则以下结论:①abc>0;②2b+c>0;③若图象经过点(-3,y1),(3,y2),则y1>y2;④若关于x的一元二次方程ax2+bx+c-3=0无实数根,则m<3.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每小题4分,共24分)
11.(2023广东揭阳揭西期末)皮影戏是一种以兽皮或纸板做成的人物剪影,在灯光照射下用隔亮布进行表演的民间戏剧.“皮影戏”中的皮影是 (填写“平行投影”或“中心投影”).
12.(2023广东深圳中考)小明从《红星照耀中国》《红岩》《长征》《钢铁是怎样炼成的》四本书中随机挑选一本,其中拿到《红星照耀中国》这本书的概率为 .
13.(2023湖北孝感中考)已知一元二次方程x2-3x+k=0的两个实数根为x1,x2,若x1x2+2x1+2x2=1,则实数k= .
14.(2023湖南岳阳中考)2023年岳阳举办以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在A处用仪器测得赛场上一宣传气球顶部E处的仰角为21.8°,仪器与气球的水平距离AD为20米,且距地面高度AB为1.5米,则气球顶部离地面的高度EC是 米.
(结果精确到0.1米,sin 21.8°≈0.371 4,cos 21.8°≈0.928 5,tan 21.8°≈0.400 0)(M9228005)
15.【半角模型】如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A、C分别在x轴、y轴上,B(2,2),函数y=(x>0)的图象与边AB、BC分别交于点D、E,连接OD、OE、DE.若∠DOE=45°,则k的值为 .
16.【易错题】(2023辽宁抚顺清原三模)如图,在矩形ABCD中,AB=3,BC=6,点E是射线BC上一动点,将△ABE沿AE翻折得到△AFE,延长AF交CD的延长线于点G,当BE=3EC时,线段DG的长为 .
三、解答题(共66分)
17.[含评分细则](8分)(2022贵州贵阳中考)在初中阶段我们已经学习了一元二次方程的三种解法,它们分别是配方法、公式法和因式分解法,请从下列一元二次方程中任选两个,并解这两个方程.
①x2+2x-1=0;②x2-3x=0;③x2-4x=4;④x2-4=0.
18.[含评分细则](10分)(2023安徽马鞍山和县二模)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-3,-1),B(-4,-4),C(-1,-3).
(1)以点O为位似中心,在第一象限作出△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的相似比为1∶1;
(2)以点O为旋转中心,将△ABC顺时针旋转90°后得△A2B2C2,请作出△A2B2C2;
(3)直接写出cos∠BAC的值.
19.[含评分细则](10分)(2023四川内江市中二模)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(1,4)、B(4,n).
(1)求这两个函数的表达式;
(2)请结合图象直接写出不等式kx+b≤的解集;
(3)若点P为x轴上一点,△ABP的面积为6,求点P的坐标.
20.[含评分细则]【项目式学习试题】(12分)(2023浙江绍兴模拟)根据以下素材,探索完成任务.
如何调整足球的发球方向
某足球场的一部分如图所示,球门宽DE=CF=7 m,高CD=EF=2.51 m.小梅站在A处向门柱CD一侧发球,点A正对门柱CD(即AC⊥CF),AC=24 m,足球运动的路线是抛物线的一部分
如图,当足球运动到最高点Q时,高度为4.5 m,即QB=4.5 m,此时水平距离AB=15 m,以点A为原点,直线BA为x轴,建立平面直角坐标系
问题解决
求足球运动的高度y(m)与水平距离x(m)之间的函数关系式,并判断此时足球能否入网
小梅改变发球方向,发球时起点不变,运动路线的形状不变,判断足球能否打到远角E处入网
上述任务1、任务2中球落在球门边线视同球入网
21.[含评分细则](12分)(2022四川德阳中考)如图,AB是☉O的直径,CD是☉O的弦,AB⊥CD,垂足是点H,过点C作直线分别与AB,AD的延长线交于点E,F,且∠ECD=2∠BAD.
(1)求证:CF是☉O的切线;
(2)如果AB=10,CD=6,
①求AE的长;
②求△AEF的面积.
22.[含评分细则]【分类讨论思想】(14分)(2022四川遂宁中考)如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点A的坐标为(-1,0),点C的坐标为(0,-3).
(1)求抛物线的解析式;
(2)【最短距离问题】如图1,E为△ABC边AB上的一动点,F为BC边上的一动点,D点坐标为(0,-2),求△DEF周长的最小值;
(3)如图2,N为射线CB上的一点,M是抛物线上的一点,M、N均在第一象限内,B、N位于直线AM的同侧,若M到x轴的距离为d,△AMN的面积为2d,当△AMN为等腰三角形时,求点N的坐标.
答案全解全析
1.D 只有选项D中图形能找到一个点,使图形绕该点旋转180°后与原来的图形重合,所以是中心对称图形.故选D.
2.B 俯视图如下:
故选B.
3.A ∵关于x的一元二次方程x2-4x+k=0无实数解,
∴Δ=(-4)2-4×1×k<0,解得k>4.故选A.
4.B 如图,过点A作AH⊥BB1于点H,则四边形AHB1A1是矩形,∴AH=A1B1,∠BAH=α.在Rt△ABH中,∵cos α=,∴AH=acos α,∴A1B1=acos α.故选B.
5.C 由题得N(2,2),M(1,2),Q(1,3),T(2,3),P(3,1),∵2×2=4,1×2=2,1×3=3,2×3=6,3×1=3,2<3=3<4<6,∴常数k的值从1逐渐增大到9的过程中,图象l依次经过的格点的顺序是点M→同时经过点P,Q→点N→点T,故选C.
6.D ∵∠C=20°,∠BPC=70°,∴∠BAC=∠BPC-∠C=50°=∠BDC,∵AB是☉O的直径,∴∠ADB=90°,∴∠ADC=∠ADB-∠BDC=40°.故选D.
7.A 选项A,设p=,∵点(0.2,500)在这个函数的图象上,∴500=,∴k=100,∴p与S的函数关系式为p=,原说法正确;选项B,当S=0.5 m2时,p==200 Pa,原说法不正确;选项C,当S>2 m2时,p<50 Pa,原说法不正确;选项D,p随S的增大而减小,原说法不正确.故选A.
8.D ∵直线y=k1x+4与y轴交于点C,∴点C的坐标为(0,4),∴OC=4.如图,过B作BD⊥y轴于D,∵S△OBC=2,∴BD=1,∵tan∠BOC=,∴OD=5,∴点B的坐标为(1,5),∵点B在反比例函数y=的图象上,∴k2=1×5=5.故选D.
9.D 如图,设CH与GF交于点M,∵四边形DEFG是正方形,∴GF∥DE,∠GDE=∠DGF=90°,∴△CGF∽△CAB,∴.∵CH⊥AB,∴∠DHM=90°,∴四边形DHMG是矩形,∴DG=MH,∵CH=h,正方形DEFG的边长是x,∴MH=x,CM=CH-MH=h-x,又AB=c,∴.故选D.
10.C ①∵抛物线y=ax2+bx+c的顶点A的坐标为<0,∴ab>0,又当x=0时,y=c>0,∴abc>0,故①正确,符合题意;②∵直线x=-是抛物线的对称轴,∴-,∴a=b,由图象可得x=1时,y=a+b+c<0,∴2b+c<0,故②错误,不合题意;③设(-3,y1),(3,y2)两点到直线x=-的距离分别为d1、d2,则d1=,∴d2>d1,根据图象可得,抛物线上的点距离对称轴越近,对应的函数值越大,∴y1>y2,故③正确,符合题意;④∵关于x的一元二次方程ax2+bx+c-3=0无实数根,∴Δ=b2-4a(c-3)<0,∴b2-4ac+12a<0,∴b2-4ac<-12a,∴4ac-b2>12a,∵m=,且由抛物线开口向下知a<0,∴m<3,故④正确,符合题意.故选C.
11.中心投影
解析 “皮影戏”中的皮影是在灯光照射下形成的影子,是中心投影.
12.
13.-5
解析 ∵一元二次方程x2-3x+k=0的两个实数根为x1,x2,∴x1+x2=3,x1·x2=k,∵x1x2+2x1+2x2=1,∴k+2×3=1,解得k=-5.∵方程有两个实数根,∴Δ=b2-4ac=(-3)2-4k≥0,解得k≤,∴k=-5符合题意.
14.9.5
解析 由题意,得四边形ABCD是矩形,∴AB=CD=1.5 m.在Rt△ADE中,∵∠EAD=21.8°,AD=20 m,∴DE=AD·tan 21.8°≈20×0.400 0=8(m),∴CE=CD+DE=1.5+8=9.5(m),即气球顶部离地面的高度EC约是9.5 m.
15.-4+4
解析 如图,延长BC至F,使得CF=AD,连接OF.∵四边形OABC是正方形,∴∠OAD=∠OCF=∠AOC=90°.在△OAD和△OCF中,CF=AD,∠OAD=∠OCF,OA=OC,∴△OAD≌△OCF(SAS),∴OF=OD,∠COF=∠AOD.∵∠DOE=45°,∴∠AOD+∠COE=45°,∴∠COF+∠COE=45°,即∠EOF=45°,∴∠EOF=∠DOE.在△DOE和△FOE中,OD=OF,∠DOE=∠EOF,OE=OE,∴△DOE≌△FOE(SAS),∴DE=EF.∵B(2,2),∴OA=OC=AB=BC=2.∵D、E在函数y=(x>0)的图象上,∴k=2AD=2CE,∴AD=CE.设AD=CE=x,则BE=BD=2-x,DE=2x.在Rt△BDE中,BD2+BE2=DE2,∴2(2-x)2=(2x)2,解得x1=-2-2(不合题意,舍去),x2=-2+2.
模型解读 半角模型:由一个大角和它的一半小角组成的共顶点且大角两边相等的基本几何模型.常见的半角模型有“45°半角模型”“60°半角模型”,基本图形如下:
解半角模型的一般步骤:①找旋转中心(含半角的角的顶点),构造旋转;②证全等;③利用全等得到边角关系.
16.或8
解析 如图①,当点E在线段BC上时,设EF交AD于K.∵BC=6,BE=3EC,∴EC=,∵四边形ABCD是矩形,∴∠ADC=∠ADG=90°,AD∥BC,∴∠DAE=∠AEB=∠AEK,∴AK=EK,设AK=EK=x,∵∠AFK=∠B=90°,AF=AB=3,FK=,∵tan∠DAG=.如图②,当点E在线段BC的延长线上时,设EF交AD于K.∵BC=6,BE=3EC,∴EC=3,EB=EF=9.∵四边形ABCD是矩形,∴∠ADC=∠ADG=90°,AD∥BC,∴∠DAE=∠AEB=∠AEK,∴AK=EK,设AK=EK=y,∵∠AFK=90°,AF=AB=3,FK=9-y,∴y2=32+(9-y)2,∴y=5,∴FK=EF-EK=4,∵tan∠DAG=,∴DG=8.
易错点 易忽视点E在BC的延长线上的情况.
17.解析 ①利用公式法:x2+2x-1=0,
Δ=22-4×1×(-1)=4+4=8,
∴x=.
∴x1=-1+.
②利用因式分解法:x2-3x=0,
∴x(x-3)=0.
∴x1=0,x2=3.
③利用配方法:x2-4x=4,
两边都加上4,得x2-4x+4=8,
∴(x-2)2=8.∴x-2=±2.
∴x1=2+2.
④利用因式分解法:x2-4=0,
∴(x+2)(x-2)=0.
∴x1=-2,x2=2.
(注:任选两个即可,每个4分,共8分)
18.解析 (1)如图,△A1B1C1为所作.3分
(2)如图,△A2B2C2为所作.6分
(3)cos∠BAC=.10分
详解:∵AB=,
∴AB=BC.如图,取AC的中点D,
则BD⊥AC,
在Rt△ABD中,∵AD=,
∴cos∠BAD=.
19.解析 (1)把A(1,4)代入y=,得m=4,
∴反比例函数的表达式为y=.2分
把B(4,n)代入y=,得n=1,
∴B(4,1).3分
把(1,4)、(4,1)代入y=kx+b,
得
∴一次函数的表达式为y=-x+5.5分
(2)不等式kx+b≤的解集为0
则点C的坐标为(5,0).8分
∵△ABP的面积为6,
∴PC×1=6,
∴PC=4,9分
∴点P的坐标为(1,0)或(9,0).10分
20.解析 任务1:由题意,得抛物线顶点坐标为,1分
设抛物线解析式为y=a(x+15)2+,2分
∵抛物线经过点A(0,0),∴225a+=0,
解得a=-,3分
∴y=-,
∴足球运动的高度y(m)与水平距离x(m)之间的函数表达式为y=-.4分
当x=-24时,y=-=2.88>2.51,
∴足球不能入网.6分
任务2:足球运动路线形状不变,连接AF,此时以点A为原点,AF所在直线为x轴,以过点A的铅垂线为y轴建立平面直角坐标系,易得抛物线的函数关系式仍为y=-.8分
∵FC=7,AC=24,∠FCA=90°,
∴AF==25,10分
当x=-25时,y=2.5<2.51,
∴能打到远角E处入网.12分
21.解析 (1)证明:连接OC,如图,
∵AB是☉O的直径,AB⊥CD,
∴.∴∠CAB=∠DAB.
∵∠COB=2∠CAB,∴∠COB=2∠BAD.
∵∠ECD=2∠BAD,∴∠ECD=∠COB.2分
∵AB⊥CD,∴∠COB+∠OCH=90°,
∴∠OCH+∠ECD=90°,∴∠OCE=90°.
∴OC⊥CF.3分
∵OC是☉O的半径,
∴CF是☉O的切线.4分
(2)①∵AB=10,∴OA=OB=OC=5,
∵AB是☉O的直径,AB⊥CD,
∴CH=DH=CD=3.
∴OH==4,6分
∵OC⊥CF,CH⊥OE,∴△OCH∽△OEC,
∴.
∴AE=OA+OE=5+.8分
②过点F作FG⊥AB,交AB的延长线于点G,如图,
∵∠OCF=∠FGE=90°,∠CEO=∠GEF,
∴△OCE∽△FGE,
∴,10分
设FG=4k,则FE=5k,∴EG==3k,
∵DH⊥AB,FG⊥AB,∴DH∥FG.
∴,
解得k=.11分
∴FG=4k=5.
∴△AEF的面积=×AE·FG=.12分
22.解析 (1)∵抛物线y=x2+bx+c经过点A(-1,0),点C(0,-3).
∴
∴抛物线的解析式为y=x2-2x-3.3分
(2)如图,设D1为D关于直线AB的对称点,D2为D关于直线BC的对称点,连接D1E,D2F,D1D2,DD2,CD2.
由对称性可知DE=D1E,DF=D2F,△DEF的周长=D1E+EF+D2F,
∴当D1,E,F,D2共线时,△DEF的周长最小,最小值为D1D2的长,4分
令y=0,则x2-2x-3=0,解得x=-1或3,
∴B(3,0),∴OB=OC=3,
∴△BOC是等腰直角三角形,5分
∵BC垂直平分DD2,且D(0,-2),C(0,-3),
∴D2(1,-3),6分
∵D,D1关于x轴对称,∴D1(0,2),
∴D1D2=,
∴△DEF的周长的最小值为.7分
(3)如图,连接BM.
∵M到x轴的距离为d,AB=4,∴S△ABM=2d,
又∵S△AMN=2d,∴S△ABM=S△AMN,
∴B,N到AM的距离相等,8分
∵B,N在AM的同侧,∴AM∥BN,
设直线BC的解析式为y=kx+m,
则有
∴直线BC的解析式为y=x-3,9分
∵A(-1,0),AM∥BC,
∴直线AM的解析式为y=x+1,
由
∴M(4,5),10分
∵点N在射线CB上,∴设N(t,t-3),
过点M作x轴的平行线l,过点N作y轴的平行线交x轴于点P,交直线l于点Q.
∵A(-1,0),M(4,5),N(t,t-3),
∴AM=5,
MN=.11分
当AM=AN时,5,
解得t=1±,
当AM=MN时,5,
解得t=6±,
当AN=MN时,
,
解得t=,
∵N在第一象限,∴t>3,
∴t的值为或1+或6+,
∴点N的坐标为或(1+)或(6+).14分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
